永磁直线同步电机直接推力控制系统推力脉动的分析与优化

王桂荣，张世桃

（中国计量学院 机电工程学院，杭州 310018)

永磁直线同步电机直接推力控制系统推力脉动的分析与优化

王桂荣，张世桃

（中国计量学院 机电工程学院，杭州 310018)

针对永磁直线同步电机（PMLSM）的传统直接推力控制（DTFC）系统中推力脉动的问题，推导了PMLSM的推力与电机功角的关系公式，并基于此公式分析了扇区划分方法对电机推力的影响。研究了采样频率和逆变器开关频率的关系对电机推力的影响。提出了一种限制逆变器开关频率的扇区细分的DTFC控制方法。在理论分析的基础上，建立了基于SIMULINK的仿真模型，对传统直接推力控制系统和优化后的直接推力控制系统进行了对比仿真，仿真结果表明该方法有效地减小了DTFC控制系统的推力脉动的幅值。

PMLSM；DTFC；扇区细分；逆变器开关频率；采样频率

0　引言

直接转矩控制由于其控制方式简单、便于实现全数字化控制、转矩响应快而得到了广泛关注[1]。直接推力控制（DTFC）则是在直接转矩控制（DTC）的基础上发展起来的一种专门用于直线电机的控制方法。文献[2,3]指出，在感应电机与永磁同步电机的DTC控制系统中，均会出现电压矢量对转矩的影响与期望不符的情况，从而造成不合理的转矩脉动。文献[5,6,8]提出了在异步电机的DTC控制系统中采用扇区细分的方法，但除了少量文章分析了其对称性原因外，其他文章并未做原因分析，未能指出扇区划分方法对转矩的影响。针对以上两个问题，本文推导了PMLSM的电磁推力与电机功角的关系，分析了直线电机中电压矢量对推力的影响，并从推力与功角关系的角度分析了扇区划分方法对电机推力的影响。研究了在DTFC控制系统中，变化的开关频率对推力脉动的影响，指出了对逆变器的开关频率加以限制必要性。提出了一种限制逆变器开关频率的扇区细分的新型DTFC控制方法。仿真结果表明，该方法有效减小了PMLSM的推力脉动。

1　PMLSM电磁推力与电机功角关系的推导

为简化推导过程，作如下假设[6]：

1）初级三相绕组采用Y型连接，且各项绕组的匝数、电阻值均相等；

2）忽略反电势的谐波，即假设反电势为正弦波；

3）电机铁芯导磁系数无穷大，忽略磁路饱和、涡流和磁滞损耗；

4）忽略动子及永磁体的阻尼；

5）电机无凸极性。

基于以上假设可得PMLSM在d-q坐标系中的电压方程为：

磁链方程为：

推力方程为：

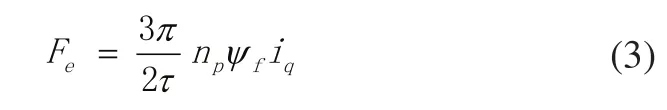
式中，ud、uq分别为d、q轴电压；id、iq分别为d、q轴电流；Ld、Lq分别为d、q轴电感；ψd、ψq分别为d、q轴定子磁链；ψf为永磁体磁链；Fe为电机推力；R为相电阻；p为微分算子；v为电机运行速度；τ为极距；np为磁极对数。

由于扇区细分法的主要变量为电机功角，为了便于分析，本文对以上公式作如下变换，以期得到电机推力与功角的直接关系。

记C1=pLd+R、C2=pLq+R、C3=ωLd、C4=ωLq，经等价变换可得：

又由假设式(5)电机无凸极性可得Ld=Lq，则可记A1=C1=C2、A2=C3=C4，则有：

记d-q系中的合成电压矢量为us，则有：

式中δ为定子磁链矢量和转子永磁体之间的夹角。综合式(3)、式(6)、式(7)得：

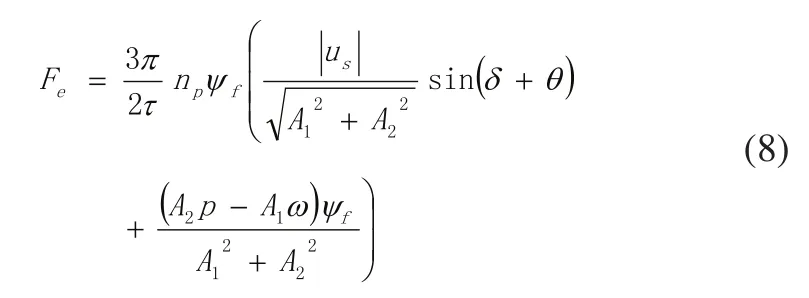
式中θ的定义为：

理想状态下，忽略电机运行过程中的参数变化，则对同一电机而言，当其稳定运行时，其速度亦恒定，即ω为常数。又有np、τ、ψf、p、A1、A2、|us|、θ均为常数，则有Fe只与δ有关。

2　扇区划分方法对推力的影响及优化方法

传统的DTFC控制是将定子磁链圆平均分成6个扇区，每个扇区60°（如图1所示），根据定子磁链所在扇区、实际推力大小及实际定子磁链大小选择电压矢量，以实现对电机推力的直接控制[7,8]。电压矢量选择表如表1所示。表中U0、U7为零电压矢量，只改变磁链的旋转速度，不改变其幅值大小。Δψs=1或0表示要求增加或减小磁链大小，ΔFe=1或-1表示要求增加或减小推力大小，ΔFe=0表示推力大小不变。

图1　传统DTFC控制的扇区划分

由第2节可知θ为常数，为了便于分析电压矢量对电机推力的影响，本文将d-q坐标系沿逆时针方向旋转θ角度，得d'-q'坐标系。则在d'-q'坐标系中式(8)可化为：

表1　传统直接推力控制电压矢量选择表（逆时针）

为解决该问题，本文将扇区进一步细分，缩小了δ'的变化范围，以确保推力单调性在该扇区中始终保持一致。细分后的扇区及电压矢量选择表分别如图2和表2所示。表2（图2）中分别由与其相邻的两基本电压矢量合成得到，即由U1和U5合成，U2'由U2和U3合成，依此类推。其他变量的意义同表1（图1）。

图2　细分后DTFC控制的扇区划分

表2　细分后直接推力控制电压矢量选择表（逆时针）

同样以扇区I为例，当ψs'处于该扇区时，由表2知可选择的电压矢量分别为U0、U7、U2、U6、U1'、U5'，则δ'的变化范围为或正弦函数在这些区间内的单调性均固定，即推力关于功角在这些区间内的单调性固定，确保了推力的实际变化方向和指令期望的变化方向相一致。

3　采样频率与逆变器的开关频率的关系对电机推力的影响及优化方法

传统DTFC控制系统中，磁链误差和推力误差经Bang-Bang控制器控制逆变器的开关状态。当Bang-Bang控制器采样到推力误差状态改变时，根据设定改变其输出状态，选择不同的电压矢量，经PWM变换后控制逆变器开关状态的切换[8]。在该过程中采样和改变逆变器开关状态并不一定同时完成，如图3所示。图中Tr、Ts、To分别代表实际推力误差状态时序、采样时序和逆变器状态切换时序。其中，采样模块在Ts上升沿时采样实际推力误差状态，逆变器在To上升沿时切换开关状态。

图3　限制前状态切换时序图

图中T1时刻实际误差状态发生跳变，此时Ts处于上升沿（实际中会有所滞后），采样模块对实际推力误差状态进行采样，采样结果经Bang-Bang控制器处理后将间接改变逆变器的开关状态。但如图3所示，由于实际状态改变时，To并没有处于上升沿，逆变器必须要等待ΔTo的时间，直到下个上升沿到来时才可以切换开关状态，这便造成了调节滞后的问题。且如果在ΔTo的时间内采样结果再一次发生改变的话，则上一次的采样结果将不会被处理，造成对推力误差状态信息的丢失。这两点均对DTFC系统的推力控制产生了不利影响。

因此本文尝试对采样频率和逆变器的开关频率加以限制，即逆变器的开关频率必须是采样频率的整数倍，且大于其最小开关频率，Ts与To的上升沿必须同时到来。由于在同一个系统中采样频率是固定的，逆变器的开关频率亦随之固定。如图4所示，逆变器的开关频率是采样频率的两倍，且小于逆变器的最大开关频率，确保了Ts与To的上升沿同时到来。这样当输入到采样模块的实际误差状态发生改变时，制器便可以同时间接改变逆变器的开关状态，及时调整输出电压矢量的状态，确保了对电机推力的及时调整。

图4　限制后状态切换时序图

4　传统DTFC与优化后的DTFC的对比仿真与分析

基于以上分析，本文分别搭建了传统DTFC系统与优化后的DTFC系统的仿真模型，对这两种系统进行了对比仿真。指令速度均为0.2m/s，采样频率为10kHz，优化后的逆变器的开关频率为20kHz，逆变器的最高开关频率为30kHz。扇区细分导致需要增加的电压矢量U1'、U2'、U3'、U4'、U5'、U6'分别由与其相邻的两基本电压矢量按50%的占空比合成得到。图5～图7分别为电机空载、带恒定负载和带变化负载时的对比仿真图。表3为优化前后电机空载、带恒定负载和带变化负载时推力脉动的幅值的正向典型值、负向典型值及宽度（正向典型值、负向典型值之差）。

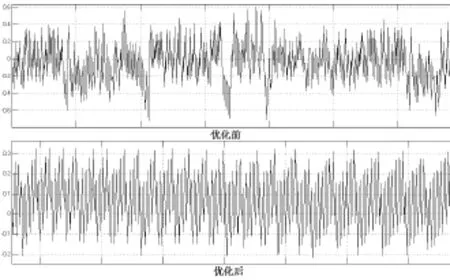
图5　空载时推力脉动对比图

图6　带恒定负载时推力脉动对比图

图7　带变化负载时推力脉动对比图

表3　优化前后推力脉动幅值表

如图5～图7及表3所示，在电机空载、带恒定负载和带变化负载三种情况下，与优化前相比，优化后的DTFC控制系统的推力脉动的幅值均明显减小。且优化后推力脉动的波形更加规则，这为通过系统补偿的方式进一步减小推力脉动提供了可能。

5　结论

本文推导了PMLSM的电磁推力与电机功角的关系，指出了传统DTFC控制系统中推力关于功角在单一扇区内的单调性不确定，而电压矢量选择表却是固定的，导致了电压矢量对推力的影响与期望不一致。指出了传统DTFC控制系统中，逆变器的开关状态未能及时根据采样状态的改变而改变，造成调节滞后。提出了限制采样频率和逆变器开关频率的扇区细分的新型DTFC控制方法。仿真结果表明，新型DTFC控制系统有效减小了电机的推力脉动。

[1] Buja G S,Kazmier Kowski M P, Direct torque control of PWM inverter-fed AC motors-a survey[J],IEEE Trans. on Industrial Electronics,2004,51(4):744-757.

[2] 郭前岗,李耀华,孟彦京.直接转矩控制中电压矢量对电磁转矩的影响[J].中小型电机,2004,31(6):6-9.

[3] 李耀华,刘卫国.永磁同步电机直接转矩控制不合理转矩脉动[J],电机与控制学报,2007,11(2):149-151.

[4] 钱坤,谢寿生,高梅艳,等.改进的直接转矩控制在异步电机中的应用[J].中国电机工程学报,2004,24(7):210-214.

[5] Yen-Shin Lai, Member, IEEE, Jian-Ho Chen. A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction[J],IEEETrans. Energy Convers, 2001,16(3):220-227.

[6] 廖晓钟,邵立伟.直接转矩控制的十二区段控制方法[J].中国电机工程学报,2006,26(6):167-173.

[7] 陆华才,提娟,高文根,陈其工.永磁直线同步电机全速无位置传感器控制[J],电机与控制学报,2013,17(4):93-94.

[8] M. Vasudevan, Dr. R. Arumugam. New direct torque control scheme of induction motor for electric vehicles[A].5th Asian Control Conference, Melbourne[C].2004:1377-1379.

[9] Zhouhui Tan, Yongdong Li, Min Li. A Direct Torque Control of Induction Motor Based on Three-level NPC Inverter[J], IEEE PESC, 2001, 3: 1435-1439.

[10] 李崇坚.交流同步电机调速系统[M].2版.北京:科学出版社,2013:270-285.

Analysis and optimization of force ripple on traditional DTFC system for PMLSM

WANG Gui-rong, ZHANG Shi-tao

TP13

A

1009-0134(2016)02-0092-04

2015-10-23

国家自然科学项目基金（61203113）；浙江省自然科学基金 （LY15F030012）

王桂荣（1975 -），女，浙江杭州人，副教授，博士，主要从事嵌入式系统的开发与应用研究。