多轴车床非圆车削加工的实现

2016-11-29李广正李佳伟周茂书

制造业自动化 2016年2期

关键词：车床凸轮圆弧

李广正，李佳伟，周茂书

（中国工程物理研究院机械制造工艺研究所，绵阳 621900）

多轴车床非圆车削加工的实现

李广正，李佳伟，周茂书

（中国工程物理研究院机械制造工艺研究所，绵阳 621900）

创新性的提出了一种非圆车削加工方法，非圆车削相比与铣削加工方式具有刀具适应性强的特点，加工特殊结构零件时能极大的提高加工效率、降低成本。该方法利用多轴车床现有功能，通过增加Y轴运动，解决了传统非圆车削中不可避免的刀具工作角度变化的问题，同时讨论了非圆规则截面车削的编程方法，通过加工验证该方法是可行的。

非圆车削；多轴车床；偏心圆弧；刀具工作角度

0　引言

车削加工和铣削加工是机械加工中最常用的两种加工方式，其各自有明确的加工对象、刀具以及编程方法。传统的车削方法只能加工回转类结构的零件。对于非圆截面（如凸轮）或是回转体上有凸台等结构的零件，传统车床是无法加工的。

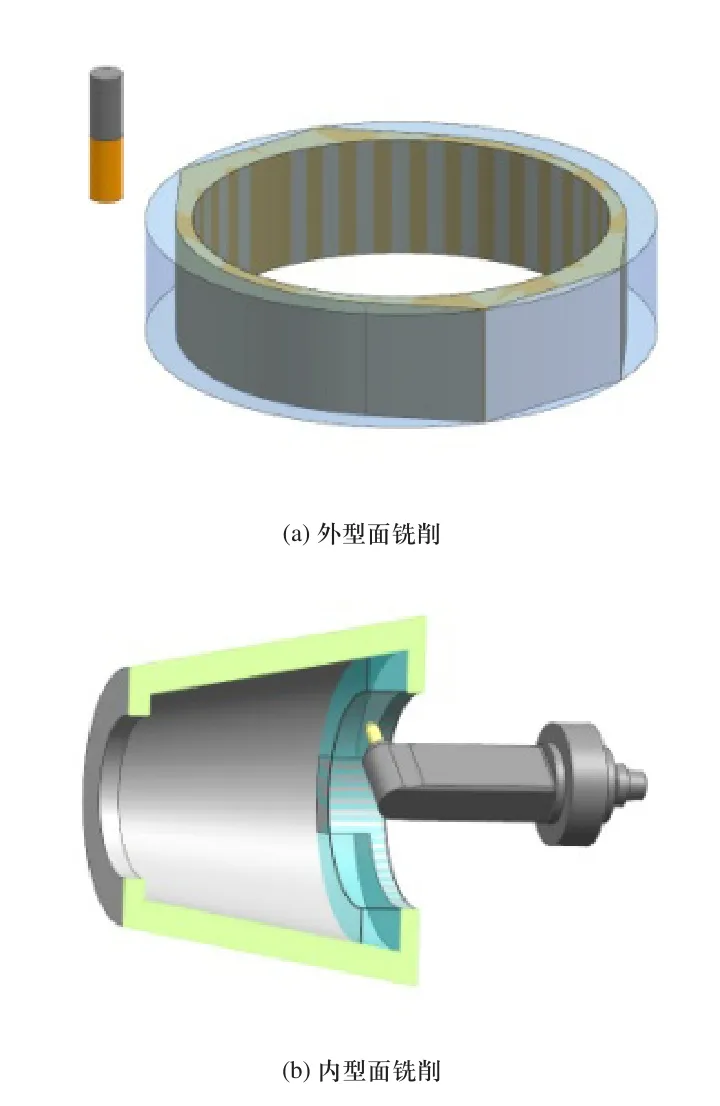
图1　典型的非回转体零件加工

如图1所示，若采用侧刃铣削外型面，则要求刀具具有较长的刃长，而在对工件内腔进行铣削时，为了避免刀具干涉，常采用角度头加球头铣刀的加工方式，刀具刚度减弱，切削条件恶劣，切削表面质量差且切削效率也受到影响。而车削过程中切削路径为连续轨迹，切削质量通常较高，且车刀不受工件曲率半径约束，对零件适应性较好。因此，对于特殊的非回转体类零件，以车代铣是工艺优化的方向。

从几何形状上看，非圆截面上各处径向尺寸随转角连续变化，为了实现非圆截面的车削，最直接的方式就是在一个车削回转周期上进行快速的X轴径向插补，文献中利用UG和MALAB软件生成可用于车床的数控代码[1]，但是此时刀具的工作前后角随着转角不断变化，尤其是在非圆度较大的地方。这种切削角度不断变化会引起切削力波动，影响加工表面质量，还可能存在负后角的地方，发生刀具干涉。文献[2]基于传统两轴机床，设计了一种复合机构，控制刀具的位置与姿态，使刀具保持理想的工作角度，但是需要额外的运动机构和控制系统，实现起来较复杂。

为了实现恒定的刀具工作角度，笔者利用机床已有的功能，在不增加额外运动机构的情况下，提出了一种新的非圆截面车削加工方案。

1　恒角度非圆车削实现

凸轮为典型的非圆零件，如果把凸轮作为驱动件，从动件为假想刀具，接触点为假想切削点，则研究凸轮机构中接触点的运动轨迹可以帮助理解刀具在非圆车削时的运动轨迹与姿态。根据从动件的几何形状，可分为三种情况：1）尖底；2）滚子；3）平底，三种凸轮机构及其对应接触点的法向矢量示意如图2所示。

图2　凸轮机构接触点法向矢量示意

刀具的工作基面是根据切削速度矢量建立的，根据文献[2]，非圆车削时的合成切削速度方向即为非圆轮廓曲线过切削点的瞬时切线方向。在尖底和滚子凸轮机构中，过接触点的瞬时切线方向都在不断变化，因此为了实现恒定刀具工作角度，需要根据非圆轮廓调整刀具的姿态。而在平底凸轮机构运动过程中，接触点在非圆轮廓上的切线方向保持为水平方向，此时接触点并不在对称中心处，若刀具的切削点与凸轮接触点重合，此时刀具有恒定的工作角度。

传统车削加工一般要求刀心通过工件回转中心以获得理想的工作角度，而在非圆车削中，为了实现切削过程中刀具恒定的工作角度，则要求刀具“偏心”，这也是非圆车削中刀具恒定工作角度实现的关键。

笔者利用的是一台配备有SIMENS840D系统的具有CXYZ四轴联动的车床，从原理上能够满足上述非圆车削的要求。然而要实现车削加工，还需要数控程序的支持。

2　编程方法

常规的车削仅需要对XZ轴进行编程，即对回转体母线轮廓进行编程，主运动为主轴回转。而非圆车削是对单个截面进行编程，即CXY轴编程，主运动为C轴进给，车削完一个截面C轴进给360°，编程方式类似于加工中心。

目前的数控插补以直线和圆弧插补为主，本文也仅讨论由直线和圆弧组成的非圆截面的车削编程。事实上，任意曲线都能以给定的误差用圆弧曲线和直线进行拟合，因此采用本文的加工方式，理论上能够实现任意非圆轮廓的车削[3]。

本节首先讨论单段直线和圆弧轮廓的编程方法，然后再讨论各段在相切和相交时两种情况的编程。本节示意图的视图均为操作者朝向主轴方向，主轴顺时针旋转为正。

2.1单段轮廓的编程方法

2.1.1同心圆弧的车削

圆弧圆心位于工件回转中心，此情况即为常规的车削，此时刀具定位到象限点，保持静止，C轴进给，其运动示意如图3(a)所示，编程格式为：

其中X值为圆弧半径值， IC为圆弧的角度增量。

2.1.2直线的车削

由于直线的法向矢量为恒定的，因此在直线段的车削时，刀具仅产生Y轴位移对工件进行拉削，此时C轴静止，其运动示意如图3(b)所示，编程格式为：

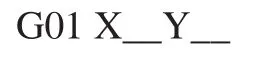
图3　非圆车削运动示意图

2.1.3偏心圆弧的车削

前面两种情况，或者刀具静止或者C轴静止，运动关系比较清楚，当圆心不在回转中心时，实际运动轨迹为C轴进给与刀具进给的合成运动。

以逆时针圆弧BC为例，如图4所示，其圆心为点A，假定工件静止，则切削路径为C到B。首先工件及刀具需要定位到位置1所示，此时AC平行于OX轴，当切削到终点位置时，圆弧与刀具实际处于位置2，ABC绕O点顺时针旋转变换成A'B'C'，此时线段A'B'平行于OX轴。易知该过程中C轴旋转角度等于圆弧BC对应的圆心角，即圆心角∠AOA'等于圆心角∠BAC。

更进一步，在OX轴插入点O'，使得OO'=AC=A'B'，由于线段AC和A'B'均平行于OX轴，则四边形OACO'和OA'B'O'都构成了平行四边形，使得O'C=OA=OA'=O'B'，则点C、B'落在圆心为O'的圆弧上，其半径值为回转中心距BC圆弧中心点A的距离。由于B点的任意性，因此在刀具切削圆弧BC上任意一点时，其实际切削点都落在圆弧CB''上，则切削点（刀具）的实际运动轨迹为圆弧CB’。

图4　偏心圆弧车削示意

在明确了工件及刀具的运动轨迹后，可以得到该类圆弧加工的编程格式为：

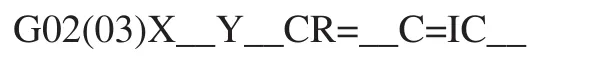
其中XY为终点B'的坐标值，IC为偏心圆弧对应圆心角。

当切削圆弧为顺时针方向时，可以得到相同的结论。需要说明的是，如图4所示，切削的圆弧CB为逆时针方向，而刀具的实际轨迹圆弧CB'为顺时针方向，因此在G02/G03的判断上要与常规相反，且CR值为回转中心到圆弧中心距离，而非圆弧BC的半径值。

2.2轮廓间过渡

由于在任意切削点位置，该点的法向矢量都要满足与X轴线平行，因此在每段轮廓加工开始前，工件都先进行定位，以满足矢量要求，通常选择直线段作为初始加工轮廓。在进行下一段轮廓加工时，如果轮廓之间保持相切，切点处法向矢量保持不变，则工件不需要重新定位，加工程序只需把各单段轮廓连接起来即可。

图5　相交轮廓处过渡示意

若相邻轮廓不相切，则需要在两段轮廓之间增加一行过渡程序段，对工件进行定位，以满足切削起始点的法向要求。如图5所示，在相交点B处，刀具与切削点B相对位置保持固定，C轴进给，因此刀具做圆弧插补，圆心为回转中心，重新定位后，工件与刀具从位置ABC变换成位置A'B'C'，该程序段刀具实际不发生切削。过渡段编程格式如下：

其中XY为定位完成后终点B'坐标值，CR为回转中心到切削点距离，IC为上一段轮廓结束到下一段轮廓开始C轴需要定向的角度增量，若该角度值为正值，则圆弧应为顺时针，若角度值为负值，则圆弧应为逆时针。

3　试验结果

图6为一非圆轮廓，轮廓关于X轴对称，由1段直线和3段偏心圆弧组成，在点A、D处轮廓相交，其余轮廓相切。试验件采用2A12硬铝进行车削，机床为DMG公司生产的四轴车床，数控系统为SIMENS840D。

图6　非圆试验件尺寸图示及加工程序

常规多轴车床中C轴的使用一般用于对工件进行定位和分度，即使在程序段中进行多轴的编程，C轴与各轴也是分步进给的，但本文提出的非圆车削方法中，C轴与XYZ进给轴必须进行联动才能实现准确的切削路径，因此需要在程序中加入FGROUP(X,Y,Z,C)程序段，此命令用于协同各轴进给速度，此后程序段中F值单位为度/每分钟，程序尾调用FGROUP()取消。

试验件中非圆车削等效每转进给为0.2，车削表面粗糙度小于Ra3.2，通过引入宏变量，还可以实现变截面的车削，相比于铣削方式，加工更灵活。