改进型扰动观测器在伺服系统中的应用

毛仁超，丁 干

(中国船舶重工集团公司第七〇一研究所，武汉 430064)



改进型扰动观测器在伺服系统中的应用

毛仁超，丁 干

(中国船舶重工集团公司第七〇一研究所，武汉 430064)

工业环境中广泛存在的外部扰动是影响交流伺服系统性能的重要因素。该文以转矩反馈控制为基础，分析实际系统中速度检测延时会导致扰动观测器延时失配的问题，进而影响观测器的观测效果。通过对观测器输入进行延时匹配，同时增加延时补偿环节，改善观测器的观测效果，并提升观测器带宽，最后分析加入改进观测器后系统的参数鲁棒性。实验结果证明，改进的扰动观测器为系统的抗扰性能带来有效提升。

转矩反馈；扰动观测器；延时匹配；延时补偿

0 引 言

交流伺服系统因其优良的动态特性以及较高的控制精度在工业制造中大量使用，然而工业环境中广泛存在的外部扰动却对伺服系统控制的效果产生重要的影响[1]。虽然传统的PI控制能够抑制外部扰动带来的影响，但是其抗扰能力受限于系统的开环增益；此外，PI控制反馈调节的本质导致了其对于扰动克服的滞后性，难以满足高精度机电系统对于扰动抑制的要求。George Ellis提出的扰动反馈控制，通过在电流指令中增加预估的扰动量可以在低稳定裕度的回路的系统中，在不增加回路增益的情况下提升系统的抗扰动能力，达到近似抵消扰动的目的[2]，由于运动控制系统的转矩测量设备价格较高，一般利用观测器的方法进行转矩估测。日本学者大西公平提出的扰动观测器[3]，由于结构简单易于实现，在工业中广泛使用。多年来，有不少学者对于这种扰动观测器进行了研究，梅野孝治基于两自由度控制器和因子分解逼近改进了观测器的框架[4]；文献[5-6]利用扰动观测器抑制电机转矩脉动，改善转速控制性能；文献[7]讨论了观测器的稳定性问题，并提出了参数设计的方法[7]。但是，实际系统与建立模型间存在的偏差会影响观测器的实际效果。对此，本文分析了实际系统中速度滞后对于观测器的影响，在此基础上对扰动观测器进行改进，补偿速度滞后的影响并提升观测器带宽，对改进后系统的参数鲁棒性进行分析，最后通过实验对改进效果进行了验证。

1 负载扰动观测器

扰动观测器的基本思想是将实际输出与估测对象模型输出之差作为等同干扰，将等同干扰通过估测对象模型的逆估计出扰动，扰动观测器的基本结构如图1(a)所示[8]。

(a) 基本结构

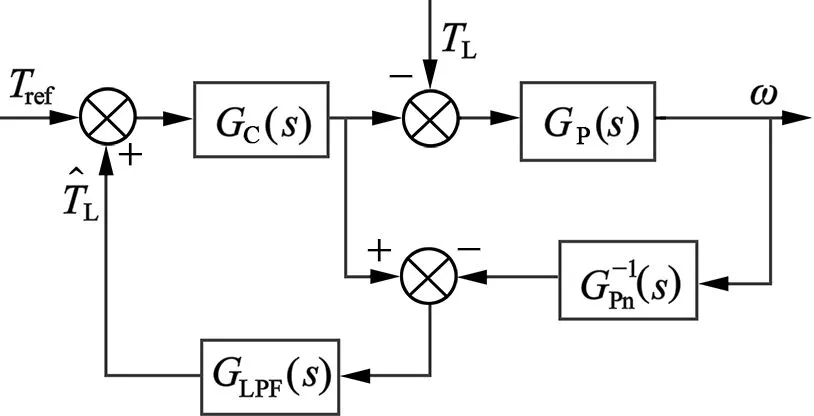
(b) 变形结构

图1 扰动观测器的结构

(1)

利用式(1)可以得到扰动观测器的实现结构如图2所示，此时负载转矩观测器没有微分项，便于实现。通过式(1)可以发现，当低通滤波器截止频率无限大时，低通滤波器近似于1，此时观测器速度较快，系统抑制扰动的能力较强；当低通滤波器截止频率较小，观测器对高频测量噪声的抑制增强，但观测器速度减慢，系统抗扰能力变差。因此低通滤波器的参数选择需要综合考虑抗扰能力和噪声抑制能力。

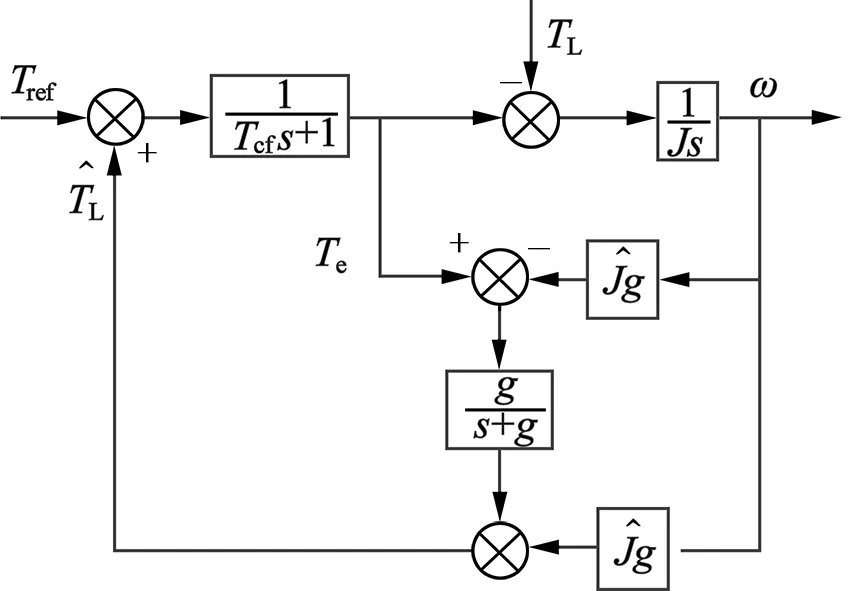
图2 干扰观测器控制结构图

2 改进负载转矩观测器

在实际系统中，电机的转速通常是利用编码器得到的位置进行微分获得。由于编码器精度有限，计算得到的速度往往存在量化误差，为了保证电机的低速性能以及较小的转矩波动，常常需要对计算得到的速度进行滤波处理。然而对速度滤波的同时将会带来速度检测的滞后，扰动观测的基本原理是通过运动方程计算出扰动转矩，从式(2)可以看到，经过处理后的速度将与输出转矩发生时间上的失配，从而导致观测的负载转矩动态性能变差。特别在一些编码器精度较低的场合，往往需要较强的滤波减小检测速度的量化误差，与此同时较大的速度延时会增强延时失配对转矩观测的影响，此时的观测器结构图如图3(a)所示。

(2)

为保证反馈速度和输出转矩的匹配，将反馈的电流进行滤波后再输入扰动观测器进行转矩观测，保证输出转矩与反馈速度的同步，改善负载转矩的观测效果，如图3(b)所示。转矩反馈控制中，观测器的带宽直接影响了系统抗扰动的效果。由于滤波匹配后带来的延时会造成观测器响应滞后，降低系统扰动响应能力，为提升抗扰效果，在扰动观测器输出增加一阶微分环节(Tfs+1)补偿速度滤波带来的延时。由于微分环节易引入噪声，此处增加一阶低通滤波消除高频噪声，补偿环节的形式如式(3)所示，其中Tf为速度检测滤波带来的延时，g2为补偿环节的低通滤波系数。

(3)

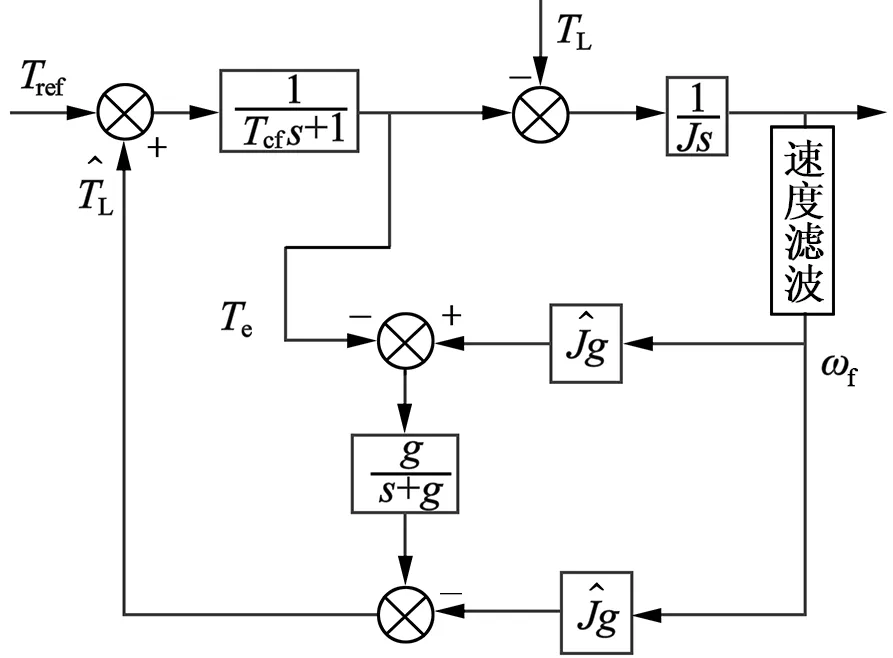
(a) 实际中存在的速度滤波滞后

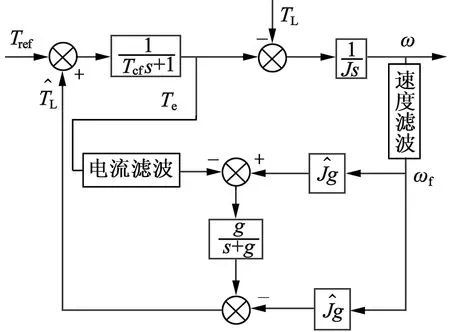
(b) 延时匹配后的扰动观测器

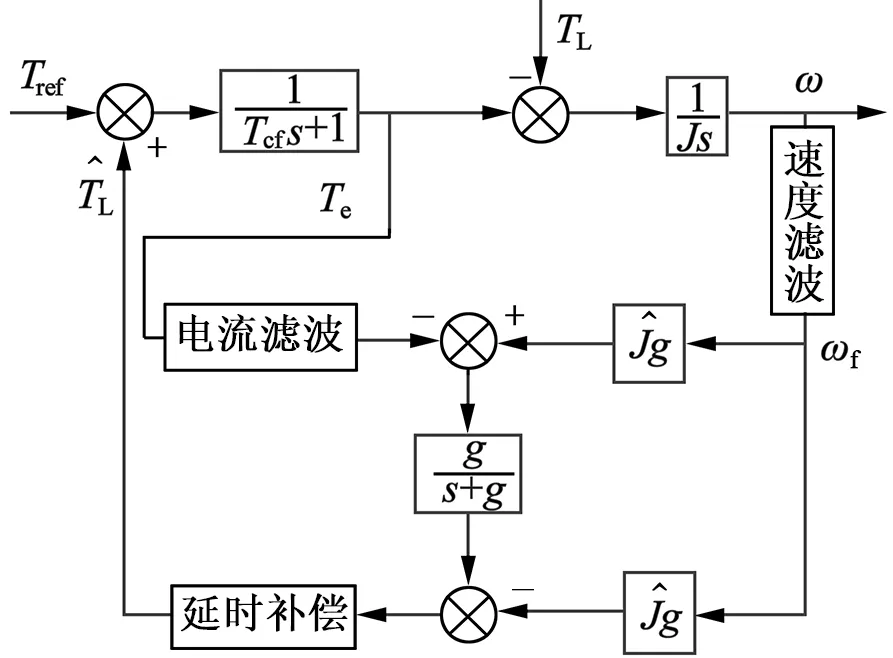
(c) 延时补偿后的扰动观测器

图3 扰动观测器

3 扰动反馈控制的参数鲁棒性

由式(1)可以看到，负载扰动的辨识依赖于系统模型，即系统惯量的大小。然而实际系统中不论是在线辨识还是离线辨识，得到的惯量与实际值之间都会存在误差，因此惯量误差对于扰动反馈控制的影响是需要考虑的。

扰动观测器的辨识基本原理依据于运动方程，当惯量存在偏差时辨识转矩如式(4)，其中ΔJ为惯量误差。可以看到，惯量的偏差影响主要在速度的微分部分，即不影响转矩的最终收敛值，但对观测器的动态过程会造成影响，若将其反馈到原系统中会影响速度响应，更严重时甚至会引起系统的不稳定。

(4)

将扰动观测器反馈到原系统如图4所示，其中扰动观测器结构如图4所示。

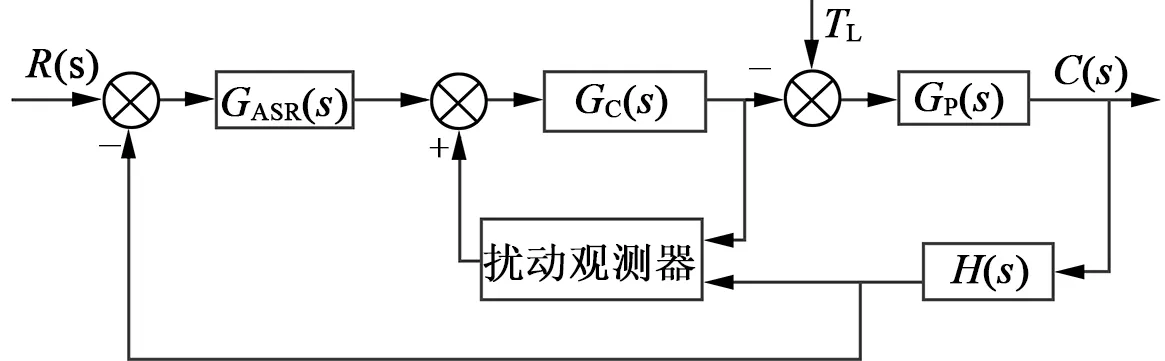
图4 扰动反馈控制结构图

由图4可得系统的闭环传递函数：

(5)

式中：GASR(s)为速度调节器，GC(s)为电流控制环路，GP(s)为被控对象，H(s)为反馈环节，通过改进后的扰动观测器的延时补偿项与速度检测延时抵消，观测器输出转矩除上力矩系数KT转化为电流指令反馈到回路，GLPF(s)为扰动观测器中的低通滤波器。

(a) g=100时的根轨迹

(b) g=2 000时的根轨迹

(c) g=5 000时的根轨迹

(d) g=10 000时的根轨迹

图5 估测惯量为变参数的根轨迹

从图5可以看到，估测惯量存在一定范围内偏差时，扰动反馈控制依然可以保持稳定，而这个稳定的范围受到扰动观测器中低通滤波系数的影响。观察可发现，当低通滤波器截止频率较高时，估测惯量偏大或偏小都会导致系统极点进入右半平面，引起系统不稳定。随着低通滤波截止频率的降低，根轨迹中右半平面内的两个极点左移，当截止频率低于一定值后，这两个极点进入左半平面，惯量的减小不再会引起系统不稳定。此外，随着截止频率的降低，导致极点进入左半平面的惯量误差也更大，系统可在惯量误差更大的范围内稳定，参数鲁棒性更好。极端情况下在低通滤波器截止频率为0时，即不加入扰动反馈时，估测惯量的偏差对于原系统没有影响。低通滤波系数对参数鲁棒性的影响如图6所示。

图6 低通滤波系数对参数鲁棒性的影响

4 实验验证

本实验平台通过两台伺服电机加联轴器对拖完成。实验驱动所用电机和对拖的负载电机均为米格的130ST-M05025，额定功率1.3kW，额定电流5A，额定转速2 500r/min，力矩系数1N·m/A，转动惯量1.06×10-3kg·m2,绕组电阻0.92Ω，极对数为4，编码器精度为17位。

抗扰性能测试时，利用与测试对象相同的电机对拖，在0.5倍额定转速下由空载突加额定转矩，记录跌落转速及恢复时间。图7为加入三种观测器后的速度启动过程及转矩观测结果，可以看到扰动观测器的加入并未改变原系统的速度响应，由于原始扰动观测器的速度和电流检测时间失配，导致利用原始观测器初始观测转矩存在较大波动，而通过延时匹配和延时补偿后的扰动观测器启动观测转矩没有太大波动。

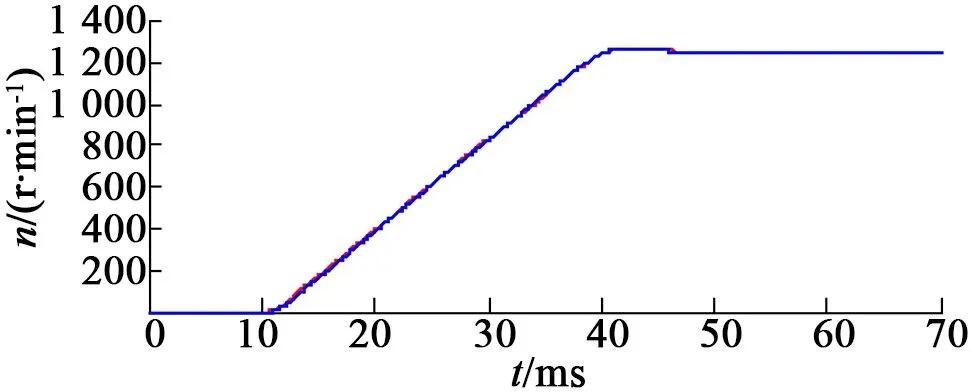
(a) 转速启动过程

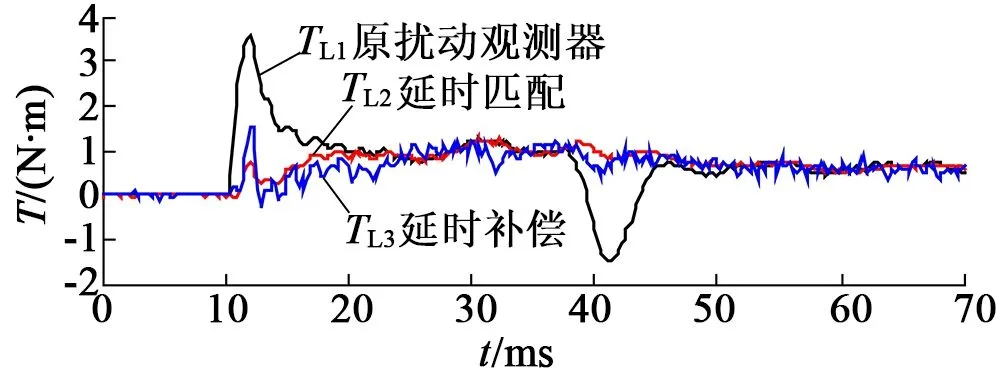
(b) 观测转矩启动过程

图7 速度与观测转矩的启动过程

三种观测器及PI的扰动响应如图8所示，可以发现，未加扰动观测器的PI控制抗扰性能最弱，突加负载力矩后速度跌落46r/min，经过31.4ms恢复到指令速度；增加原始扰动观测器的速度跌落31r/min，恢复时间为13.6ms，但速度恢复过程中存在波动；延时匹配后的速度跌落为34r/min，经过12.2ms恢复指令速度；延时补偿后的速度跌落30r/min，恢复时间为9.6ms,实验数据如表1所示。从实验结果可以看到，利用扰动观测器实现扰动反馈控制可以大大改善速度环扰动响应。此外，通过匹配电流与速度的延时，并对延时加以补偿，能够进一步完善扰动观测器，提升系统的抗扰能力。

表1 扰动反馈控制抗扰性能对比

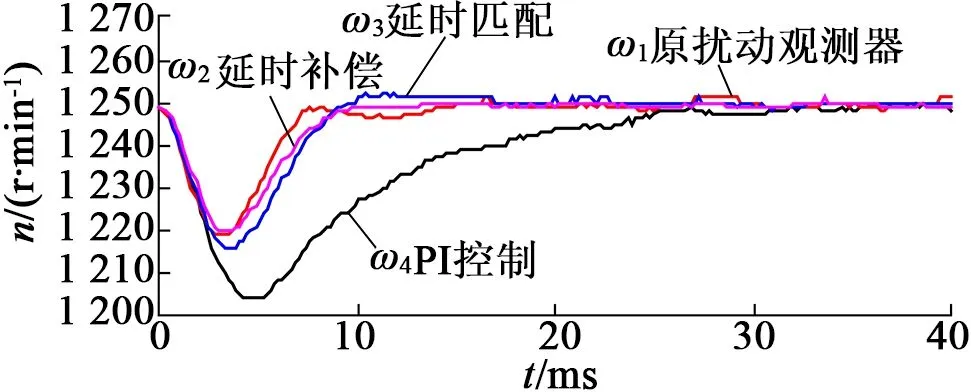
(a) 速度抗扰能力对比

(b) 转矩观测对比

图8 三种观测器扰动响应对比

5 结 语

外部扰动是影响交流伺服系统性能的重要因素，利用扰动观测器估计负载转矩，通过负载转矩反馈控制可以改善外部扰动对于系统的影响。本文在扰动反馈控制的基础上分析了实际系统中由于延时导致检测速度与输出转矩失配，进而对于扰动观测器产生的影响，通过改进的扰动观测器能在提升观测器带宽的同时解决延时失配的问题。最后通过实验验证了改进的扰动观测器在不影响原系统速度响应的同时，有效提升了电机的抗扰能力。

[1] 阮毅，陈伯时.电力拖动自动控制系统-运动控制系统[M].北京：机械工业出版社，2009.

[2] ELLIS G.Control system design guide[M].California：Elseiver Academic Press，2004.

[3] OHAISHI K.A new sevro method in mechatronics [J].Transactions of Japanese Society of Electrical Engineers, 1987，107：83-86.

[4] UMENO T,HORI Y.Robust speed contorl of DC sevro motors using modern two degeres of freedom controller design [J].IEEE Transaction on Industrial Electronics,1991,38(5):363-368.

[5] 纪科辉，沈建新.采用扰动转矩观测器的低速电机伺服系统[J].中国电机工程学报,2012,32(15):100-106.

[6] 赵希梅，郭庆鼎.基于扰动观测器和重复控制器的永磁直线同步电动机鲁棒控制[J].中国电机工程学报,2010,30(15):64-69.

[7] 于艾,杨耕,徐文立.具有扰动观测器调速系统的稳定性分析及转速环设计[J].清华大学学报,2005,45(4):521-524.

[8] 武琳.基于扰动观测器的永磁直线同步电机位置控制[M].沈阳:沈阳工业大学，2009.

Application of Improved Disturbance Observer in Servo System

MAORen-chao，DINGGan

(No.701 Institute of CSIC，Wuhan 430064,China)

The external disturbance widely existing in industrial environment is an important factor affecting performance of servo system. In this paper, based on torque feedback, the delay mismatch of observer resulting in speed delay was analyzed, which impacted on observer.Matching delay of input to observer and adding delay compensation were proposed to improve the effectiveness and bandwidth of observer. Besides that, the parameter robustness of the system with improved disturbance observer was analyzed.The experimental results prove that the improved disturbance observer has a good improvement in anti-disturbance performance.

torque feedback； disturbance observers； delay match； delay compensation

2015-12-29

TM383.4

A

1004-7018(2016)06-0070-04

毛仁超(1990-),硕士,助理工程师,研究方向为运动控制、电力拖动。