大跨桥梁地震响应分析研究

王 斌, 聂红隆

(1.内蒙古工业大学 土木工程学院，内蒙古 呼和浩特 010010;2.呼和浩特职业学院 建筑工程学院，内蒙古 呼和浩特 010070，3.宁波工程学院 经济与管理学院，浙江 宁波 315211)



大跨桥梁地震响应分析研究

王 斌1，2, 聂红隆3*

(1.内蒙古工业大学 土木工程学院，内蒙古 呼和浩特 010010;2.呼和浩特职业学院 建筑工程学院，内蒙古 呼和浩特 010070，3.宁波工程学院 经济与管理学院，浙江 宁波 315211)

从某大跨桥梁入手，分析大跨桥梁结构在不同等级地震作用下的结构响应，得出：顺桥方向地震作用下震动较为严重但不是优先发生破坏的方向，垂直于顺桥方向地震时侧移较大，为优先发生破坏的方向，在进行桥梁设计及施工时应引起重视．

大跨桥梁；地震响应；侧移

近年来,地震发生较为频繁，每年地震造成的经济损失和人员伤亡都是巨大的，同时预测地震又是世界性难题．据相关资料统计,全球每年要发生近千次破坏性地震，其中给人们带来极大危害性的也有十几起．我国提出“以桥带路”的交通思想，这不仅可以解决耕地问题，而且解决了很多地区的交通问题．桥梁结构在交通中所占位置越来越重要，地震作用下桥梁的安全状况直接关乎抢险救援．

桥梁结构的增多，使得桥梁结构的角色逐渐发生转变，逐步成为路上交通的生命线工程，所以了解其抗震性能及地震作用下桥梁结构的响应是有必要的．

陈丽丽[1]运用MIDAS进行了不对称连续刚构架的数值模拟，分别进行了反应谱分析和时程分析，得出采用箱形截面的桥梁，箱形截面高度对结构在地震作用下的内力有影响．武董[2]运用Morison方法对深水桥梁的桥墩进行了分析，探讨桥梁长期处于深水中，当发生地震时水深对桥梁的影响．张长青[3]利用MIDAS建立了主跨度为160 m的预应力刚构桥及刚腹板连续刚构桥，并对比分析两种桥型在时程响应中的不同反应．I.Sullivan[4]等人对美国斜多跨简支钢箱梁桥进行地震易损敏感性分析，得到不同桥梁斜度在相同地震作用下表现出不同的响应状况，桥梁发生损坏的位置也不相同．

汽车在桥梁行驶时发生地震的概率是存在的，如何判别地震作用下桥梁的响应状况对桥梁研究具有一定的意义．本文从大跨桥梁在地震作用下的响应入手分析其受力性能．

1 时程分析方法

桥梁时程分析方法可以分为一致激励和非致一激励．

1.1 一致激励运动方程

地基假定为刚性，所以假定地面上的物体不发生相对移动，结构内力和地面运动的反力相互平衡．根据d'Alembert原理得出：

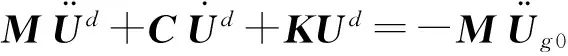
(1)

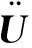
1.2 非一致激励运动方程

地基假定为刚性，但是地震在传播过程中两点之间是有时间间隔的，所以非一致激励方程为：

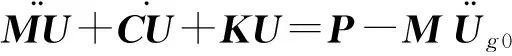
(2)

其中P为荷载．

1.3 地震作用下时程分析

时程分析理论较为成熟，地震作用下可以用统一数学表达式来分析结构受力，对线性和非线性都适用．时程分析法得到的计算结果较为接近结构实际受力结果，故时程分析法成为分析地震作用下结构受力的主要方法之一．

时程积分法基本原理是将地震动的持续时间T划分为相等的时间步长Δt，每个Δt内加速度、速度、位移等的变化规律是可以运用数学知识求出来的，后一个时间段Δt内的加速度、速度、位移等参量可以利用前一刻Δ(t-1)的已知数据求出，即将Δ(t-1)作为已知量利用微分方程求解Δt未知量．

2 大跨桥梁时程分析

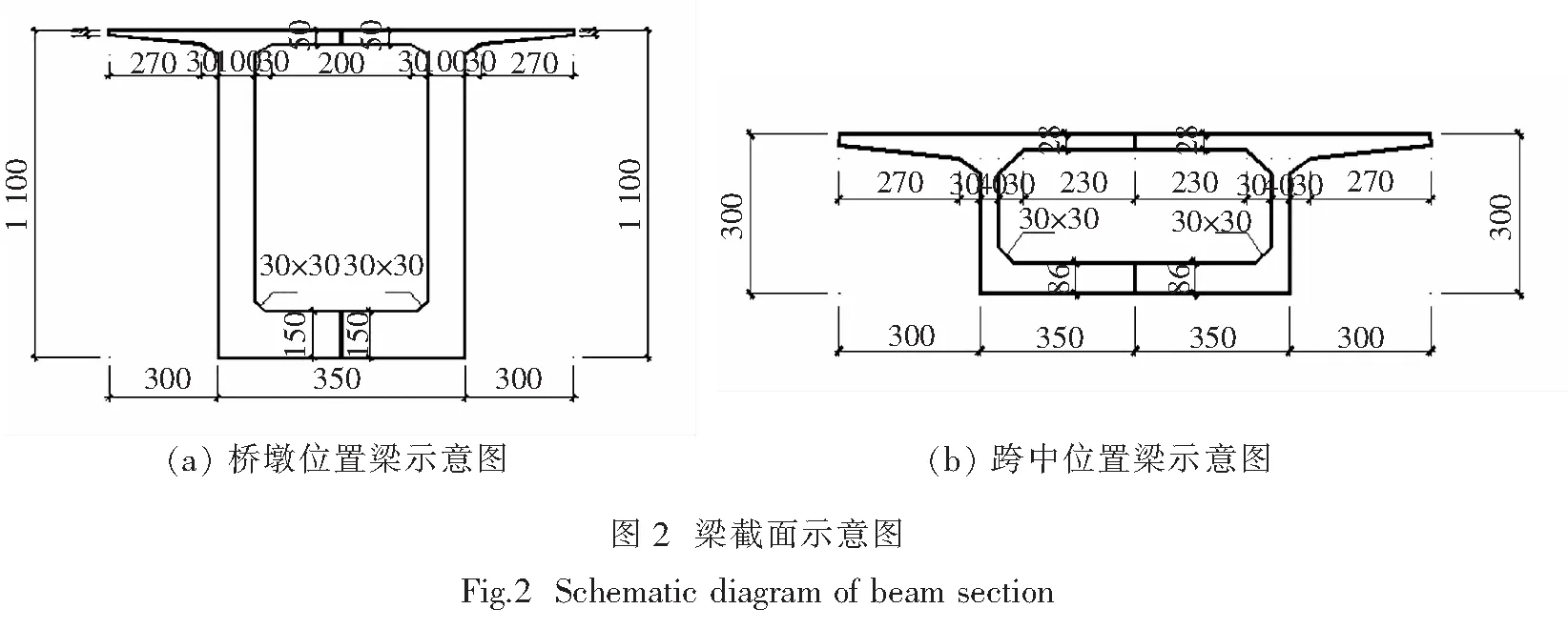
某大跨桥梁跨径为100 m+200 m+100 m，桥梁的总体布置图如图1所示．

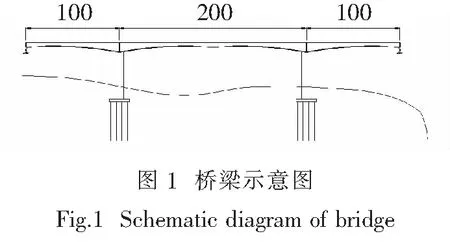
主跨量采用箱型梁(单箱)，桥墩位置梁高为11 m，主梁跨中为3.5 m，主梁沿跨径方向为二次抛物线变化曲线，主梁全宽13 m，单箱底板宽为7 m，顶板悬臂3 m，单箱主跨梁截面如图2所示．桥墩为薄壁空心墩，采用桩基础，场地类别为二类，地震设防烈度按不同等级进行考虑(计算分析是忽略桥墩在地震下的反应，只研究桥面响应)．根据[5]，时程分析所用地震加速度最大值如表1所示．

由表1可以看出，8度多遇小于7度基本，8度基本小于7度罕遇．选取EL-Centro波作为时程输入的波形(EL-Centro波形如图3所示)，我国规范对不同等级的地震虽然做了规定，但是将EL-Centro波以不同等级形式输入时只是调整峰值大小，波形的曲线并没有改变，鉴于此，借鉴表1，选取峰值加速度为200 cm/s2、400 cm/s2以及620 cm/s2．考虑地震的三相输入．

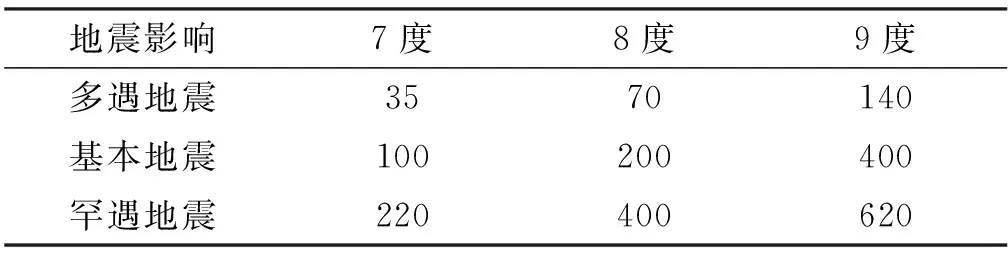
表1 时程分析所用地震加速度时程的最大值

此大跨桥梁属于对称结构，故对计算桥梁模型进行简化，简化的计算模型如图4所示．

表2 自振周期及自振频率

振型自振周期/s自振频率/Hz12.5300.39521.7800.56230.1407.143

3 结果分析

3.1 结构模态

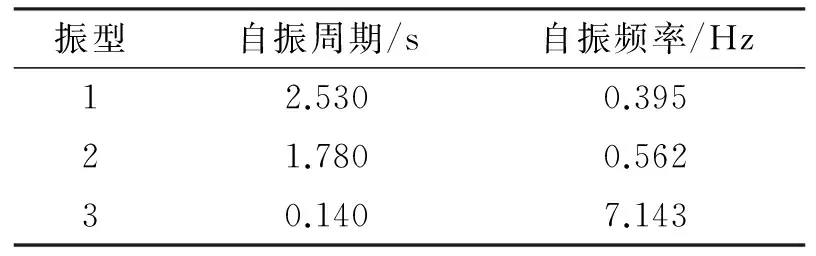
结构的振型、频率和周期是结构的固有特性，反应结构动力学特性的重要参数．分析结构模态，获得结构前3阶振型、自振周期和自振频率．图5给出了结构的前3阶振型．表2列出了结构前3阶振型的自振周期和自振频率．

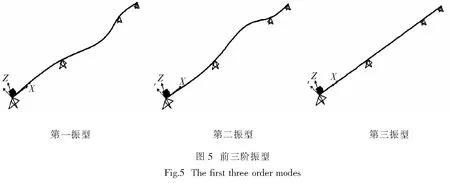
桥梁自振周期及自振频率对桥梁的养护及加固有重要的意义，但是由于桥梁体型不一，造型多变，故没有统一的桥梁经验计算公式．

本文三跨简支桥梁第一振型自振周期2.53 s，相当于150 m左右的剪力墙体系的高层钢筋混凝土结构自振周期，定性分析是符合计算规律的．

3.2 桥面响应

考虑三向地震计算后中间跨桥面中点在不同地震加速度下的地震响应,如图6所示．

加速度峰值为200 cm/s2时，桥梁结构x向地震加速度响应远大于y向及z向地震加速度响应，而速度响应及位移响应y向及z向大于x向，表明此桥梁地震作用下x向震动较为厉害，即地震时车辆通过桥梁驾驶员很难平稳行驶．桥梁发生破坏取决于桥梁的侧移，地震前15 s时刻y向侧移较大，15～30 s时刻z向侧移较大，表明桥梁在地震作用下容易发生y向的破坏，即桥梁的侧向倾覆，这与历次发生地震中桥梁的破坏模式是一致的．

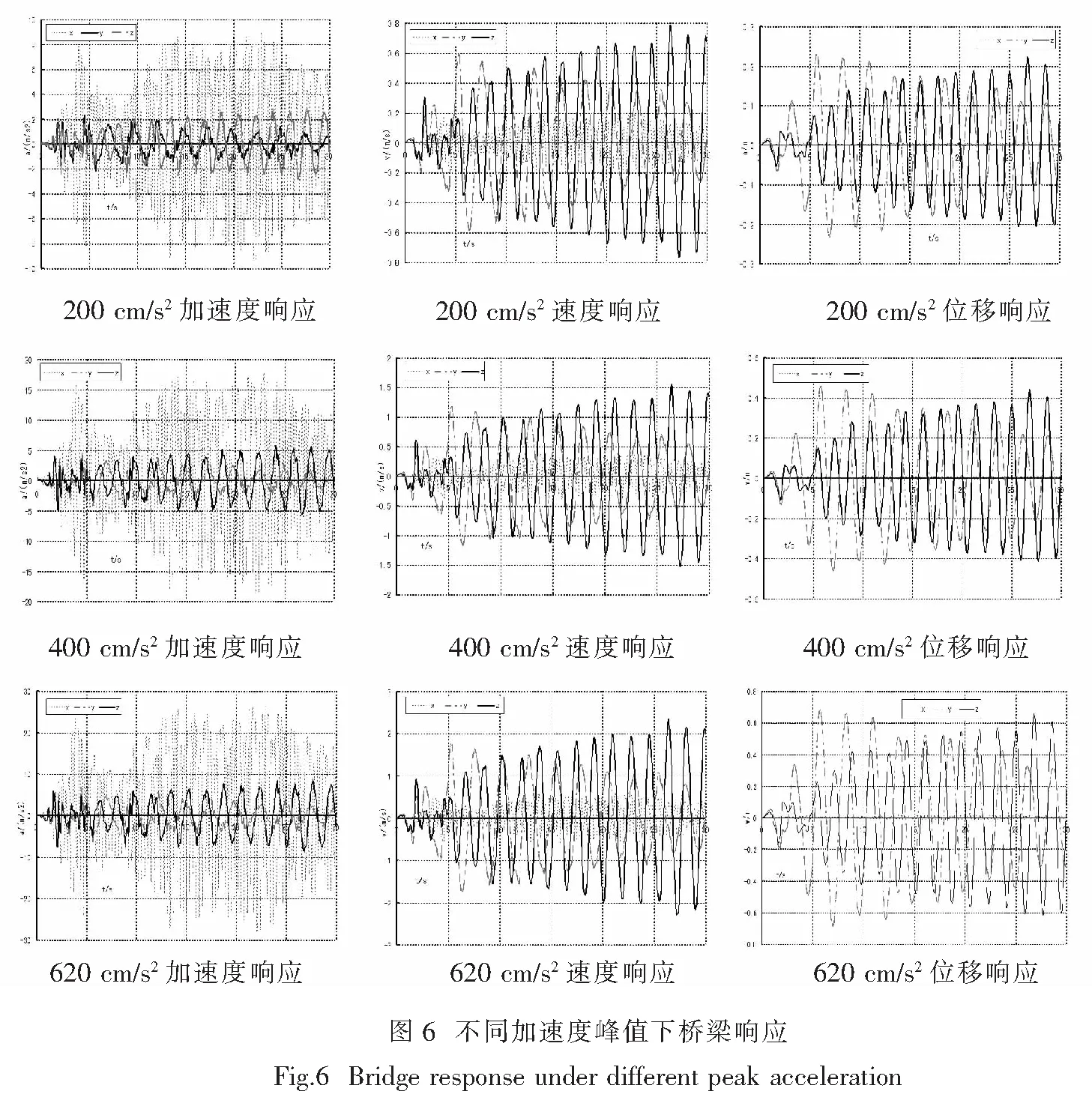
加速度峰值为400 cm/s2时，桥梁结构x向地震加速度约为y向及z向地震加速度响应的5倍，y向及z向地震加速度响应在数值上相差不大，速度响应、位移响应y向及z向大于x向．

加速度峰值为620 cm/s2时，地震作用下桥梁的响应状况与200 cm/s2及400 cm/s2规律性相差不大．

计算模型中没有考虑桥墩的影响，在一定程度上计算结构不具有代表性，后续研究可将桥墩与桥梁进行统一建模，更为客观真实地反应桥面及桥墩在地震作用下的响应及破坏状况．

此桥梁结构的地震响应在数值上随着不同地震加速度峰值的变化而变化，总体趋势为随着地震加速度峰值的提高而提高，但桥梁响应的图形一致．

4 结 论

通过分析某桥梁在不同峰值加速度下结构跨中节点的加速度、速度及位移响应，得出顺桥方向震动较为厉害，地震时车辆在桥上难以行驶，桥梁首先发生破坏的方向为垂直于顺桥方向，在进行桥梁设计及施工时应引起重视，桥梁的抗侧刚度应具备充足的安全储备．

[1] 陈丽丽.不对称连续刚构桥地震响应分析[D].大连:大连理工大学，2010.

[2] 武董.超深水高墩桥梁的地震响应分析[D].西安:长安大学,2010.

[3] 张长青,安永日,安里鹏.波形钢腹板连续刚构桥的地震响应分析[J].桥梁建设,2011(3)：17-21.

[4] SULLIVAN I,NIELSON B G. Sensitivity analysis of seismic fragility curves for skewed multi-span simply supported steel girder bridges[DB]. ASCE，2010.

[5] 建筑抗震设计规范:GB 50011—2010[S].

责任编辑：龙顺潮

Seismic Response Analysis of Long-span Bridges

WANGBin1，2，NIEHong-long3*

(1.School of Civil Engineering, Inner Mongolia University of Technology, Hohhot 010010;2.School of Architecture and Engineering, Hohhot Vocational College, Hohhot 010070；3.School of Economics and Management, Ningbo University of Techonlogy,Ningbo 315211 China)

This paper starts with a long span bridge. The structural response of long-span bridge structures under different earthquake levels is analyzed. It is concluded that the earthquake motion under the direction of the bridge direction is more serious but it is not the direction of the destruction. Horizontal displacement of bridge under earthquake is bigger. It is the direction of destruction. Attention should be paid to the design and construction of the bridge.

long-span bridge; seismic response; lateral displacement

2016-01-13

聂红隆(1968-)，男，江西 新余人，博士，教授. E-mail:niehonglong@yeah.net

U441

A

1000-5900(2016)02-0042-04