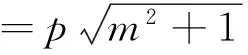一道模考解几题的一般结论及推广

江苏省昆山中学 (215300)

季刚祥



一道模考解几题的一般结论及推广

江苏省昆山中学 (215300)

季刚祥

(Ⅰ)求椭圆C的方程；

(Ⅱ)过右焦点F2的直线l交椭圆C于M，N两点，直线AM、AN分别与已知直线x=4交于点P和Q，试探究以线段PQ为直径的圆与直线l的位置关系．

这是一道散见于各地的模考解几题，原题解答如下：

(Ⅰ)(x-6)2-y2=4(过程略)；

(Ⅱ)由题意，直线l的斜率不为零，故可设l的方程为x=my+1,M(x1,y1),N(x2,y2)，由

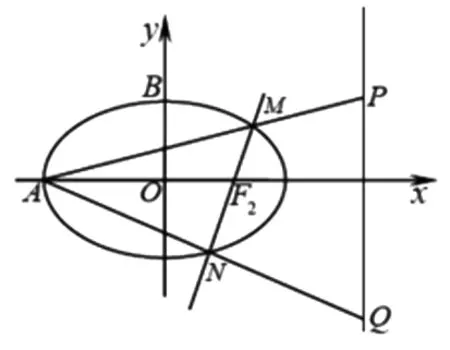
图1

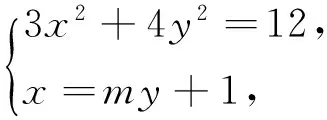
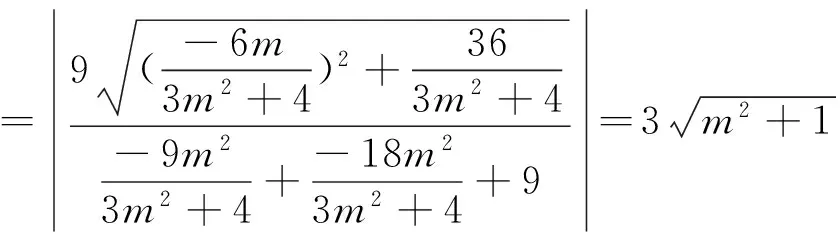
因为d=r，所以，以PQ为直径的圆与l相切.

由特殊到一般的归纳猜想及类比推理的方法容易得到如下一般性的结论

一般结论 设A是椭圆长轴的一个端点，F是焦点，过F的直线x1=x2=2交椭圆于M两点，直线(x-6)2-y2=4分别与F相应的准线l′交于点C(m，0)，则以PQ为直径的圆与直线AB切于点F.

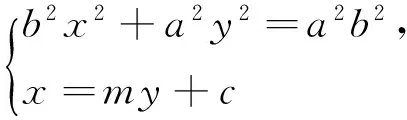
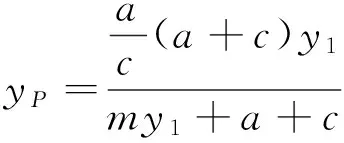
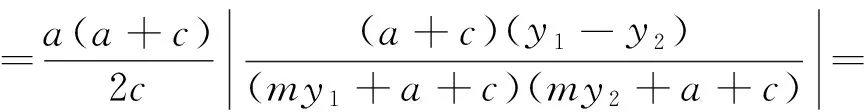
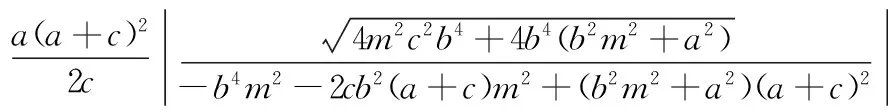
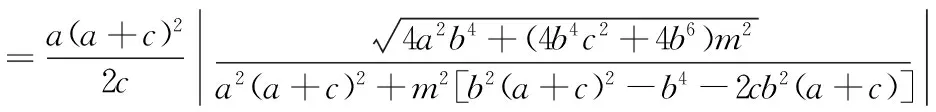
而当m=0时，显然有DF⊥l，因为d=r，所以以PQ为直径的圆与l相切于点F.

同理可证当F为左焦点l′为左准线时结论也成立(证明略)，而由对称性，其它情形结论也成立.

根据圆锥曲线的统一定义不难得到以下两种推广结论：

推广1 设A是双曲线实轴的一个端点，F是焦点，过点F的直线交双曲线于M、N两点，直线AM、AN分别与F相应的准线l′交于点P、Q，则以PQ为直径的圆与直线l切于点F.

由题意，直线l的斜率不为零，故可设l的方程为x=my+c,M(x1,y1),N(x2,y2)，

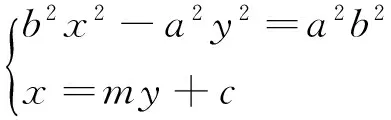
(b2m2-a2)y2+2mcb2y+b4=0，由韦达定理

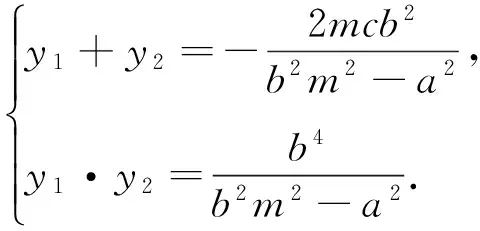
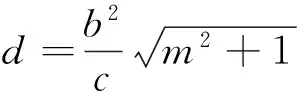
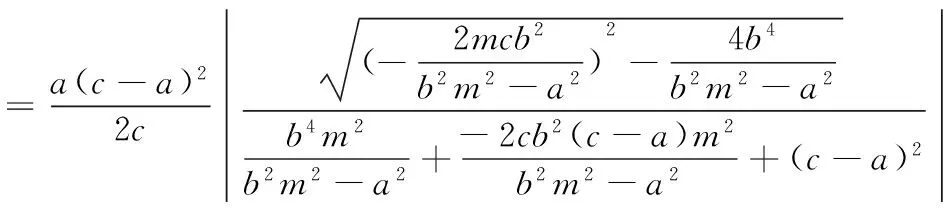
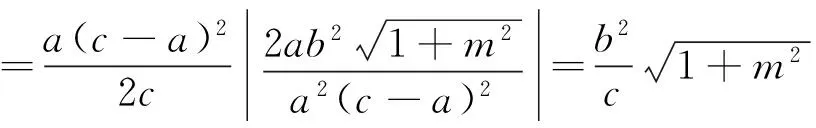
而当m=0时，显然有DF⊥l，因为d=r，所以，以PQ为直径的圆与l相切于点F.

同理可证当F为左焦点l′为左准线时结论也成立(证明略)，而由对称性，其它情形结论也成立.

推广2 设A为抛物线的顶点，F是焦点，过点F的直线l交抛物线于M,N两点，若直线AM,AN分别交抛物线的准线l′于P,Q两点，则以PQ为直径的圆与直线l切于点F.