例析运用洛必达法则求解二道导数压轴题

南昌大学附属中学 (330047)

周开财



例析运用洛必达法则求解二道导数压轴题

南昌大学附属中学 (330047)

周开财

(1)证明：当λ=0时，f(x)≥0；

(2)若当x≥0时，f(x)≥0，求实数λ的取值范围.

解法一：(1)当λ=0时，f(x)=x+e-x-1，则f′(x)=1-e-x.令f′(x)=0,解得x=0.当x<0时，f′(x)<0，∴f(x)在(-∞,0)上是减函数；当x>0时，f′(x)>0，∴f(x)在(0,+∞)上是增函数.

故f(x)在x=0处取得最小值f(0)=0，即f(x)≥0.

(2)由已知x≥0，∴e-x-1≤0.

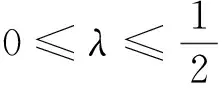
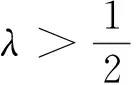
以上在处理第(2)问时对参数λ的范围分类讨论较难想到，现利用洛必达法则处理如下：

解法二：(2)由已知x≥0.

②当λ=0时，f(x)=x+e-x-1，由(1)知f(x)≥0，符合题意.

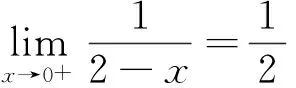
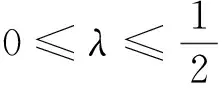
例2 设函数f(x)=ln(x+1)+a(x2-x)，其中a∈R.

(1)讨论函数f(x)极值点的个数，并说明理由；

(2)若∀x>0,f(x)≥0成立，求a的取值范围.

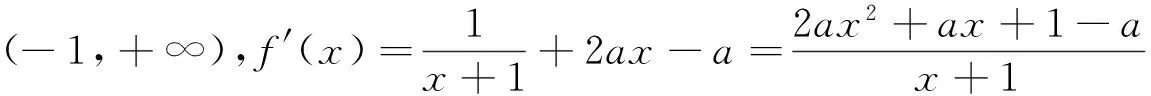
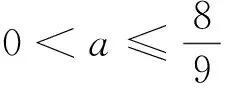
③当a<0时，Δ>0.由g(-1)=1>0可得x1<-1，当x∈(-1,x2)时，g(x)>0，f′(x)>0，函数f(x)单调递增；当x∈(x2,+∞)时，g(x)<0，f′(x)<0，函数f(x)单调递减.故函数f(x)有一个极值点.

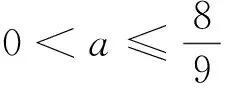
综上所述，a的取值范围是0≤a≤1.

以上在处理第(2)问时较难想到，现利用洛必达法则处理如下：

解法二：(2)由题意∀x>0,f(x)≥0成立，即a(x-x2)≤ln(x+1)恒成立.

①当x=1时，x-x2=0，原不等式为0≤ln2恒成立；

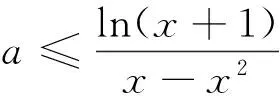
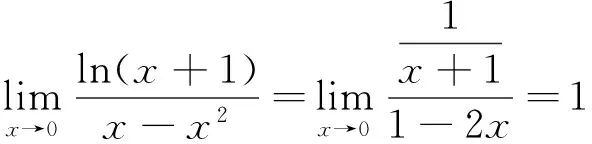
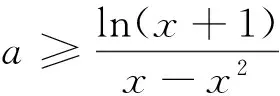
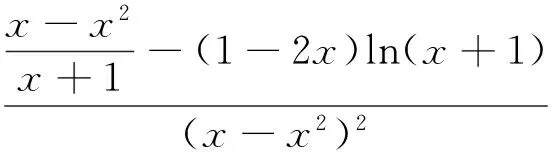
综上所述，a的取值范围是0≤a≤1.

一般地，此类含参的函数综合问题往往从三个角度求解：一是直接求解，通过对参数的讨论来研究函数的单调性，进一步确定参数的取值范围；二是凭借函数单调性确定参数的取值范围，然后对参数取值范围以外的部分进行分析验证其不符合题意，即可确定所求；三是分离参数，求相应函数的最值或取值范围，当函数的最值不好求解时，用洛必达法则往往能化难为易，使问题得到解决.