基于最优模糊控制的悬臂梁振动控制研究

杨宏斌

（榆林学院 陕西 榆林719000）

基于最优模糊控制的悬臂梁振动控制研究

杨宏斌

（榆林学院 陕西 榆林719000）

文中分析了悬臂梁的振动情况，建立了悬臂梁的动力学系统方程，设计了基于最优模糊控制算法的悬臂梁振动控制系统。系统将采集进来的信号通过最优控制理论计算得到理论输出值，建立拥有最优解的模糊控制规则，使得一个输入得到一个最优的控制输出，从而产生相应的抑制力来减弱梁的振动。使用Matlab对振动控制系统进行了仿真，结果表明该算法能够很好地抑制悬臂梁的振动。

模糊控制；最优控制；振动控制；悬臂梁

随着科学技术的不断发展，各行各业的控制技术的不断的更新，越来越多的控制理论日益成熟，如何将若干种控制理论相结合，得到取长补短的控制结果，所以，将多种控制理论相结合也是以后控制领域发展的一个重要组成部分。柔性悬臂梁作为常见力学结构，广泛的存在于生产、生活、科技、航天等多项领域中，而其振动也是影响各种柔性梁正常工作的主要因素，就需要对悬臂梁的振动进行抑制和消除，因此，臂梁的振动控制具有深远的研究意义。

1 柔性梁系统建模

柔性悬臂梁的弹性模量为E，密度为ρ，长度为L，宽度为bb，厚度为tb，梁的横截面为A，则柔性悬臂梁的振动微分方程：

式中：ω（x，t）梁的挠度；F（x，t）为梁的分布力矩；

将悬臂梁的挠度可以通过模态函数和坐标来表示：

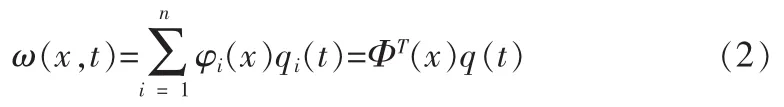
式中：Φi（x）={φ1（x），φ2（x），…，φn（x）}T；

将通过模态函数和坐标表示的挠度带入梁的振动微分方程得：

则（3）式变为：

经数学方法处理，并加入结构阻尼ξ对系统的影响，则得到系统的微分方程：

引入系统状态量：

则（5）为：

2 最优模糊控制

2.1 基本思想

模糊控制因为其优点在生产生活中广泛应用，从工程控制过程的角度出发，比较容易建立语言控制规则，其采用语言控制规则通过将操作人员或专家的相关知识直观转换为控制策略，不需要精确的数学模型，因此设计简单、易于接受和理解。又因其鲁棒性强，使得系统对外界干扰和各种外界参数的变而致使控制效果变差的影响大大减小，模糊控制又根据有经验的专家思想而建立，因此有一定的智能型，利于增强控制系统的适应力。但是随着控制规则的增加使控制精度不断提升，也会使控制系统的实时性会减弱；换言之减少控制规则的数量会提高系统的运行速度，但控制精度又会下降，因此需要在控制精度和实时性之间进行权衡。

线性二次型控制是最优控制理论的一条分支，其主要研究系统在一定外界条件下寻求一个最优的控制策略，使得性能指标函数取得极致的问题。其本质是对一个待定研究的被控对象或运动系统的控制结果的研究，使系统在要求的控制效果中从众多允许的控制方案中找出一个最优的控制方案，其性能指标值为最优。

对于同样重视控制系统的控制精度和响应速度的工程实践来说，为了取得较合适的工程控制方法，提高系统的品质和相应速度。采用最优控制和模糊控制相结合的理论进行系统控制，两种控制理论各取所长。通过传感器采集系统的偏移平衡位置的振动情况，将采集进来的信号进行量化分类，并通过最优控制理论计算得到控制系统的最优解，利用所测量的传感信号与计算出来的最优解建立模糊控制表，得到相应的模糊控制规则，通过建立的模糊控制规则进行控制，采集一个系统变量，通过模糊控制规则查找相应的最优控制量，这样既能满足系统的快速相应需求，同时有具有了最优控制精度的优点。

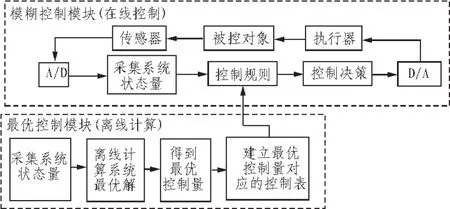
图1 最优模糊控制简图

2.2 控制步骤

1）求解控制最优解

压电柔性悬臂梁的状态空间方程为：

针对控制器所计算出的回馈信号对柔性悬臂梁振动情况的影响，这里使用由控制向量和系统状态向量共同构成的二次型性能指标函数，若取平衡位置为系统的稳定零状态，则线性二次型问题的目标函数为：

其中Q和R分别为状态变量和控输入控制变量的加权矩阵。

针对柔性悬臂梁的状态空间方程，确定一个最优解：

通过建立如下汉密尔顿（Hamilton）函数求解关于u的J（u）求极小值：

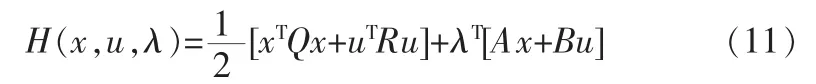
由求解汉密尔顿方程H对u的导数所构成的方程求出最优控制信号：

求解出来的最优控制信号记之为u*，则：

根据黎卡提微分方程求解矩阵P：

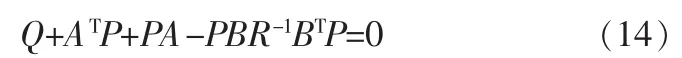
由（10）、（13）整理得出：

其中反馈增益矩阵G=R-1BTP

2）通过最优控制解建立模糊控制规则表

结合最优控制在允许控制范围下得到的最优解和模糊控制的快速相应、鲁棒性强等众多控制优点，建立拥有最优解的模糊控制规则表。通过最优控制规律求解得到最优控制量建立响应的模糊控制规则表：

表1 控制规则表

控制器首先通过由系统的输入量在线计算环节得到的最优解，所建立起拥有最优解的模糊控制规则表，极大的输入信号对应一个极大的最优控制量，极小输入量对应极小的最优控制量，以此类推。随后系统进行离线控制环节，将采集进来的输入量通过模糊控制规则表得到拥有最优解的控制输出，将输出信号作用到智能压电材料上来抑制柔性梁的振动，以实现对振动进行控制的目的。

3算 例

这里假设梁的尺寸为450×15×2 mm、密度为7×103 kg/m3。压电自感知执行器的尺寸为25×10×0.4 mm、密度1.78×103 kg/m3。根据驱动器位置优化理论，并通过柔性梁的振动进行仿真，得到将压电传感器和执行器放置于柔性梁的根部对柔性梁的振动消除效果较为明显。通过计算，一阶模态固有频率为ω1=4.793 6 rad/s，假设结构阻尼为ζ1=0.5，并对柔性梁的末端施加一个偏移量为2 mm的扰动，使用最优模糊控制规则对系统在MATLAB里进行仿真，结果如图2和图3所示。

Study on optimal fuzzy control in the cantilever vibration control

YANG Hong-bin
（Yulin University，Yulin 719000，China）

This paper analyzed the vibration of the cantilever，established the dynamic equations of a cantilever system，and designed the cantilever vibration control system based on fuzzy optimal control algorithm.The system calculated the collected signal into the output value by the theory of optimal control theory，and then the optimal solution fuzzy control rules were established by the output value.The system made the input into an optimal control output，resulting in a corresponding decrease vibration suppression force to the beam.Vibration control system using Matlab simulation results show that the algorithm can suppress vibration of the cantilever.

fuzzy control；optimal control；vibration control；cantilever beam

TN02

A

1674－6236（2016）18-0104-02

2015-08-29 稿件编号：201508162

陕西省教育厅专项科研计划项目（15JK1860）

杨宏斌 （1987-）男，陕西华阴人，硕士研究生，讲师。研究方向：智能结构及动力学系统控制。