船用雷达ARPA系统中α-β算法研究

陈福喜，杨大宁

（1.江苏科技大学 江苏 镇江 212000；2.镇江市光宁航海电子科技有限公司 江苏 镇江 212000）

船用雷达ARPA系统中α-β算法研究

陈福喜1，杨大宁2

（1.江苏科技大学 江苏 镇江 212000；2.镇江市光宁航海电子科技有限公司 江苏 镇江 212000）

α-β滤波算法是一种高效滤波算法，常用于对匀速直线运动的跟踪。为了解决船用ARPA雷达追踪定位实时性和准确性的矛盾，提出使用α-β滤波算法对目标航迹进行滤波。在确保精度要求的同时，能够快速定位目标，并计算目标运动参数，在航迹滤波中启到了非常好的效果。结合民用船舶航行速度较慢，机动性小的特点，假设目标匀速直线运动，通过均值滤波，卡尔曼滤波的仿真结果比较，最终得出α-β滤波在ARPA雷达航迹滤波中具有更强的实用性。

雷达；滤波；ARPA算法；航迹

船用导航雷达的ARPA （Automatic Radar Plotting Aid）功能主要应用于船舶避碰，雷达原始扫描数据经过数据处理后以雷达图像的形式显示，ARPA算法正是基于雷达图像的定位跟踪算法。ARPA算法通过对雷达图像扫描，获取目标位置坐标并形成运动轨迹，此时目标航迹往往包含各种噪声，与目标实际运动轨迹存在误差。因此需要运用平滑滤波算法抑制随机参数和噪声，从而估计出目标实际位置并计算目标的运动参数[1]，最终获取准确可靠的避碰参数。

航迹滤波算法在整个ARPA算法中占据重要位置，滤波算法的优劣不仅影响到运行效率，更直接关系避碰参数的准确性。目前常用的目标航迹滤波算法有3种：均值滤波，卡尔曼滤波和α-β滤波。文中结合国内船舶航行实际情况，确定模拟目标为多目标运动，主要研究α-β算法在滤波算法中在多目标运动的实际情况下如何实现滤波功能，以及和均值滤波，卡尔曼滤波的优劣对比。

1 滤波算法

1.1 均值滤波

均值滤波是一种线性滤波，常用的计算方法为邻域平均法，在船舶航迹滤波实际应用中是将连续几个相邻目标位置进行累加，然后取均值作为目标实际位置，预测方程：

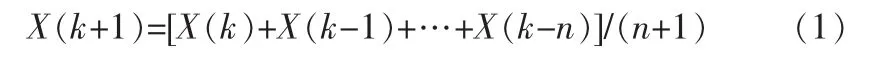
从公式（1）可以看出这种滤波方式运算简单，计算量小，工程中容易实现。但是均值滤波也存在明显的缺陷，对于毛刺噪声的抑制能力差，当在某时刻出现毛刺噪声时，均值滤波并不能很好抑制，而是通过领域平均将毛刺噪声分摊到多个位置，在最终计算目标运动状态时这些误差数值仍然存在，因此这种做法实际上并不能很好解决毛刺噪声所带来的误差，即使在均值为零的高斯白噪声中，均值滤波也并不能取得很好的航迹平滑效果。

1.2 卡尔曼滤波

卡尔曼滤波是线性无偏差最小估计的递推算法又称为最优化自回归数据处理算法[2]。它实质是通过上一次的预测，对这一时刻目标状态进行修正同时预测下一时刻目标状态，如此顺序递归，来达到滤波效果。

卡尔曼滤波的实现是通过协方差计算系统滤波增益，对目标状态实现最优估计。其中协方差的计算包括协方差预测，最优估计和新息协方差更新[3]，同时需要结合目标的状态估计，因此计算量相对庞大。而在实际工程中往往是整个系统的运行，因此必须考虑到算法的计算量和系统的实际处理能力。

1.3 α-β滤波

α-β滤波最早提出是为了提高边扫描边跟踪雷达的跟踪性能提出的[4]，是卡尔曼滤波的简化算法，主要应用于匀速运动目标的跟踪，特点在于滤波系数并不是动态计算得到，而是常数。常系数滤波特点就决定了它计算简便和运行高效，在工程上也更加容易实现。

α-β滤波也采用递归调用，通过本次观测值和先验估计值计算目标当前运动状态并建立运动模型，同时估计下一次滤波的预测值。α-β滤波采用递归调用的特点是不需要存储太多的观测值，每次调用只需要将上一次后验估计值，这样的计算方式极大提高了运行效率。

α-β滤波的滤波原理如图，其工作原理是根据本次观测值Z（k），结合上次的预测值X（k/k-1）来得到本次滤波估计值X（k）。

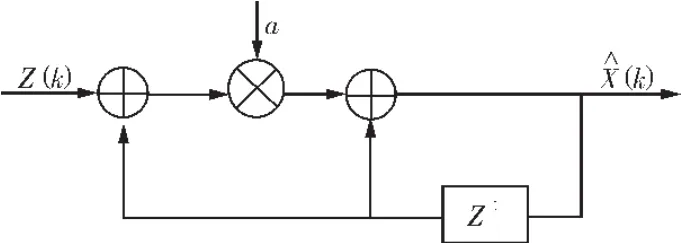
图1 α-β滤波器流程图

在滤波运算中输入为本次观测值，输出为本次滤波估计值。其中还要用到两个参数，一个是常系数α，通常系数的选择根据实际情况来确定，另一个参数为递归调用的预测值[5]。本次调用的预测值是通过上一次滤波运算的计算得到，这种递归调用的特点上面已经介绍，它的最显著特点就是简便高效。如图2是预测值的计算流程。

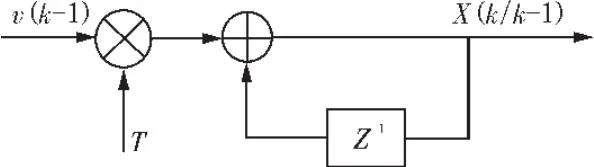
图2 α-β预测器流程图

在预测器运算中需要输入当前目标的运动状态参数，上图中T是采样时间间隔，v（k-1）为目标移动速度，X（k-1/k-2）为当前目标位置估计。通过预测器内部计算，输出即为目标下一位置的预测值X（k/k-1）。

假设目标为匀速直线运动，目标的运动状态方程为：

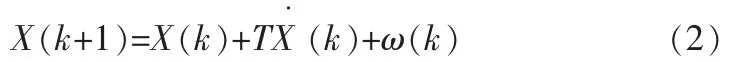
式中，X（k）为目标位置，T为采样间隔，ω（k）为高斯白噪声，目标的滤波方程为X（k）：

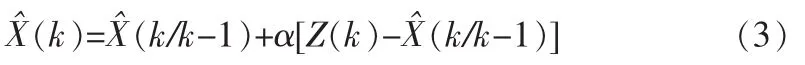
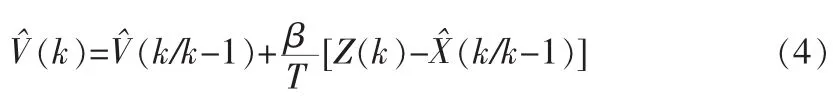
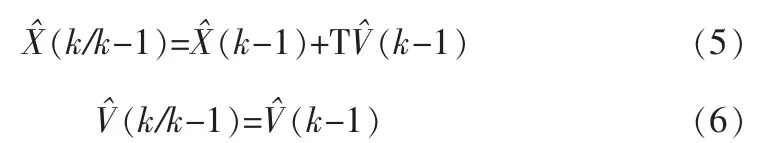
α-β滤波在船舶航迹滤波上有着无可比拟的优势，而在整个滤波计算过程中，α，β两个参数有着极其重要的位置，在此先给出关于α-β滤波器的常用系数配置，一般情况下采用临界阻尼法来选择最佳系数，通常α取值范围在0.3～0.5。对于α-β滤波器，在给定α情况下，有两种计算β值方法：

在实际仿真测试过程中我们对于不同环境下的测量值给出了最优α值选择为0.5，β值我们采用公式（7）的计算方法得到β为0.5，在确定系数情况下建立运动模型并仿真。

2 仿真分析

本次仿真采用Matlab软件，Matlab作为一门科学软件，编程方便，扩展性强，功能强大，适用于工程领域的分析计算[6]。对于本次实验仿真，首先根据雷达显示的实际船舶运动轨迹，在Matlab中模拟出目标运动轨迹。

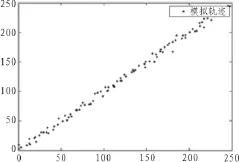
图3 模拟船舶运动轨迹

如图3在模拟的直角坐标系中，船舶位置用雷达屏幕像素点描述，船舶从原点出发，移动位置以直角坐标系中坐标位置记录，目标运动方式为匀速直线运动，并在运动轨迹中添加高斯白噪声以模拟雷达显示误差。滤波所要实现的功能是对目标轨迹的平滑滤波，下面通过实验对比均值滤波和αβ滤波的性能。

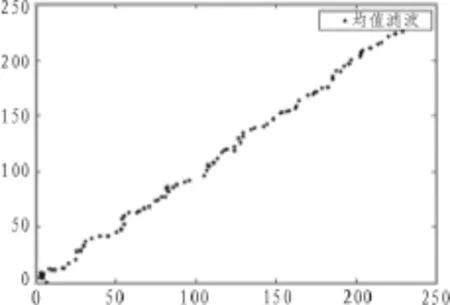
图4 均值滤波仿真结果

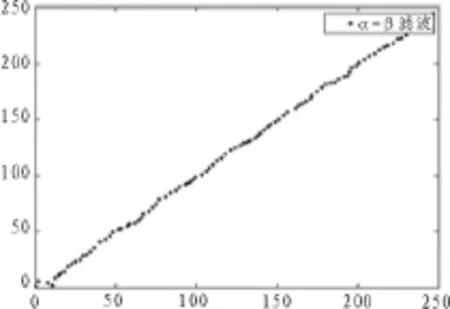
图5 α-β滤波仿真结果

对比图4和图5可以看出，图4采用均值滤波，在一定程度上得到了滤波效果，但是误差仍然较大，平滑效果不够理想。图5的航迹效果明显优于图4的航迹效果，航迹平滑，预测点误差较小。因此我们得出结论，在航迹滤波中α-β滤波要比均值滤波效果更好。

然而对于卡尔曼滤波和α-β滤波，我们采用算法复杂度的对比，通过一次滤波计算，我们分别给出如表1的统计数据。

表1 滤波算法统计

从表1中可以看出，α-β滤波的计算过程无论是加法运算次数还是乘法运算次数都远少于卡尔曼滤波，也就是说在相同系统中，α-β滤波计算速度将会比卡尔曼滤波更快。在雷达系统运行中，往往是多目标同时计算，因此在运行效率上α-β算法将会有更明显的优势。

3结 论

文中通过对均值滤波，卡尔曼滤波和α-β滤波研究，从滤波原理，滤波方式以及工程实现难易和运算的复杂度等方面对这3种滤波进行了分析，我们发现α-β滤波在滤波效果上比均值滤波要好，在算法复杂度和工程实现的角度来看明显优于卡尔曼滤波，结合船用雷达系统的软硬件考虑，认为α-β滤波在船用ARPA雷达航迹滤波中更加适合，并且通过仿真实验验证了该算法在航迹滤波中的优越性。最终将该滤波算法应用到实际船用雷达系统中，事实证明α-β滤波也确实取得了良好的滤波效果，在提高ARPA追踪准确性的同时保证了追踪实时性的。

[1]Bertrand H，Grenier D，Roy S.Experimental antenna array calibration with artificialneuralnetworks[J].Signal Processing，2008，88（5）:1152-1164.

[2]Kalman R E，Bucy R S.New results in linear filtering and prediction theory[J].Basis Eng，1961（83）:109.

[3]Welch G.Bishop G.An instroduction to the Kalman filter[R].Chapel Hill TR 95-041，2001-01-15.

[4]戴欣，郝旭.雷达多目标跟踪算法[J].信息技术，2011，10（8）:22-23.

[5]David L Hall.An instorduction to Multi-sensor Fusion[R].Beijing，International workshop on data fusion，2002.

[6]苏金明，阮沈勇.Matlab使用指南6.1[M].北京.电子工业出版社，2002.

Research on α-β algorithm of marine radar ARPA system

CHEN Fu-xi1，YANG Da-ning2
（1.Jiangsu University of Science and Technology，Zhenjiang 212000，China；2.Guanin Marine Electronics Co.，Ltd.Zhenjiang 212000，China）

α-β filtering algorithm is a kind of high efficient filter algorithm，used to track the uniform motion in a straight line.In this paper，in order to solve the contradiction of the Marine ARPA radar track positioning，such as the instantaneity and accuracy，it uses α-βfiltering algorithm to filter the target track.At the same time to ensure accuracy，it can locate target quickly and calculate the target motion parameters.α-β filtering algorithm can play a good effect at tracks filtering.Combining with the slow speed of the civil ship navigation and the characteristics of small mobility，assuming uniform linear motion and comparing the results of the average filtering with Kalman filtering.Finally，it is concluded that the alpha beta filter is more useful in the ARPA radar track filtering.

radar；filtering；ARPA algorithm；track

TN99

A

1674－6236（2016）18-0013-03

2015-09-23 稿件编号：201509163

陈福喜（1991—），男，江苏宿迁人，硕士研究生。研究方向：船用导航雷达。