可证安全的基于身份代理聚合签名方案

胡江红

（宝鸡文理学院 数学与信息科学学院，陕西 宝鸡 721013）

可证安全的基于身份代理聚合签名方案

胡江红

（宝鸡文理学院 数学与信息科学学院，陕西 宝鸡 721013）

对一个基于身份代理聚合签名方案进行了安全性分析，证明该方案的聚合签名不能抵抗伪造攻击。在此基础上，利用双线性技术构造了一个新的基于身份代理聚合签名方案，并且利用Diffie-Hellman困难问题，在随机预言模型下，证明了新方案是存在性不可伪造的.效率分析结果表明，新方案的验证等式需要3个对运算，比已有的代理聚合签名方案更安全更高效。

代理聚合签名；基于身份签名；双线性对；Diffie-Hellman困难问题

代理签名[1]能够实现数字签名权利的委托，允许原始签名者因生病，出差等原因将签名权力委托给代理签名者，代理签名者将代表原始签名者产生有效的代理签名。一个代理签名需要满足五条安全性质：可区分性、可验证性、不可伪造性、不可否认性和身份识别性.1984年，Shamir[2]第一次提出了基于身份的签名方案，解决了传统公钥密码体制中的证书管理问题。在基于身份的数字签名方案中，用户的公钥是由用户公开的身份信息得到，比如E-mail地址，IP地址，身份证号和车牌号等，而对应的私钥则是由第三方生成，这样就避免了传统的公钥密码系统对证书的发放，存储和撤销等带来的巨大开销问题。随后，随着实际应用的需要，很多学者将代理签名和基于身份的密码体制相结合，产生了基于身份的代理签名方案。2003年，Zhang和Kim[3]首次提出了一个基于身份的代理签名方案。

在实际签名中，还会涉及一些需要不同用户对不同消息进行签名，而且对许多签名同时进行验证的情况。为了提高签名的验证和传输效率，2003年，Boneh等人[4]首次提出了聚合签名的概念，即n个用户对n个不同的消息m分别进行签名，这n个签名被合成一个签名，而验证方只需要对合成后的签名进行验证就能确认是否是指定用户对消息m的签名。聚合签名大大减小了签名的存储空间和签名的验证工作量，随后出现了很多聚合签名方案[5-13]。2010年，孙华等人[13]提出了一个基于身份的聚合签名方案，随后，在此基础上又提出了一个安全的基于身份代理聚合签名方案[14]。2012年，王勇兵等人[15]提出了一个基于身份的代理聚合签名方案。文中首先对文献[15]的安全性进行分析，发现该方案不能抵抗伪造攻击，即攻击者可以成功伪造代理聚合签名，然后提出一个新的基于身份的代理聚合签名方案，利用Diffie-Hellman困难问题，在随机预言模型下，证明了新方案的安全性，而且通过效率分析发现，最终的聚合签名验证等式需要3个双线性对运算，签名长度为n+1,比文献[14]和文献[15]的效率更高。

1 文献[15]的安全性分析

这一节我们对王勇兵等人的方案进行安全性分析，具体算法参见文献[15]，这里不再详述.通过分析我们发现，攻击者能够伪造任意n个签名人对n个消息的代理聚合签名.设攻击者的身份为IDA，代理用户P1的身份为ID1，则攻击者按如下算法伪造对消息（m1，m2)的聚合签名：

首先，攻击者首先通过运行密钥生成算法得到系统公开参数，并得到与自己身份IDA对应的公私密钥对，然后，随机选择t1，t2∈，计算则攻击者伪造的对消息（m1，m2）的代理聚合签名为（Q′，V′）。由于：

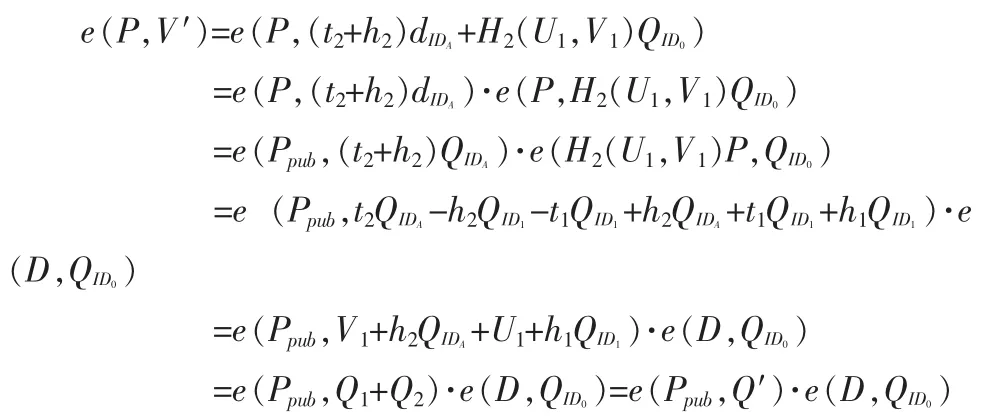
所以，攻击者伪造的聚合签名是有效的，能够通过验证等式，则文献[15]中的方案是不安全的。

2 新的代理聚合签名方案

Setup设原始签名者为O，身份信息为IDO，代理签名组为P=（P1，P2，…，Pn），相应的身份信息为IDi（i=1，2，…，n），待签名的消息为M=（m1，m2，…，mn），mw是授权证书，包括原始签名者和代理签名者的身份信息，代理签名的有效期等。

给定一个安全参数k，PKG选择两个阶为素数q＞2k的群G1和G2，一个双线性映射为e：G1×G1→G2，P是群G1的一个生成元，PKG随机选择一个随机数s∈作为系统主密钥，计算系统公钥为Ppub=sP。选择4个安全的Hash函数H0：{0，1}*→G1，H1，H2，H3：{0，1}*→，PKG公布{k，e，G1，G2，P，Ppub，H0，H1，H2，H3}，保管系统主密钥s。

Key-Extract给定用户的身份信息ID∈{0，1}*，计算QID= H0（ID）作为用户的公钥，相应的私钥为dID=sQID=sH0（ID），则记原始签名者的公私密钥对为（QID0，dID0），代理签名者的公私密钥对为（QID1，dID1）（1≤i≤n）。

Sign给定用户身份ID的私钥dID和待签名的消息m，用户随机选择 r∈，计算 U=rP，T=H1（Ppub），h=H2（m‖U），V= rT+dIDh，则对消息m的签名为（U，V）。

Veri验证者首先计算QID=H0（ID），h=H2（m‖U），然后通过下面的验证等式验证签名的有效性e（P，V）=e（T，U）e（Ppub，QIDh）

PAGen 1）原始签名者O随机选择r0∈，计算U0=r0P，h0=H2（mw‖U0），V0=r0T+dID0h0，然后将（mw，U0，V0）发送给代理签名者Pi。

2）代理签名者Pi（i=1，2，…，n）收到（mw，U0，V0）后，验证e（P，V0）=e（T，U0）e（Ppub，QID0h0）是否成立，若成立，代理者Pi计算自己的代理签名密钥xPi=V0+dIDih0。

PPASign代理签名者Pi随机选择ti∈，计算Ri=tiP，wi= H3（IDi‖mw‖mi‖Ri），Si=tiT+xPiwi，则（Si，Ri）就是身份IDi的代理签名者Pi对消息mi的签名。

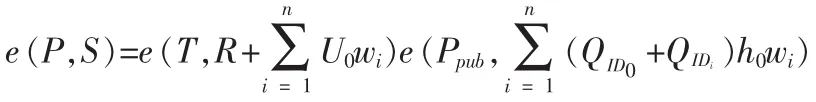
3 安全性分析

3.1 正确性

由于：

从而本方案是正确的。

3.2 安全性

由于代理聚合签名中包括授权证书，原始签名人和代理签名人的身份，因此，容易验证该方案满足代理签名的几个性质，如可区分性，可验证性，强可识别性和强不可否认性。下面我们在随机预言模型下讨论该方案的强不可伪造性。

定理1给定一个安全参数k，使G1是一个（t′，ε′）-GDH群，且其阶为素数q＞2k，p是群G1的生成元，e：G1×G1→G2是一个双线性映射，那么，本文提出的新方案在群G1上是（t，qH，qE，qS，n，ε）-抗存在性伪造安全的。

证明：假设敌手A能够以（t，qH，qE，qS，qPAS，n，ε）攻击本文新方案，其中敌手攻击者A访问哈希函数H0，H1，H2，H3询问，Extraction询问，Signing询问，Delegation询问和PPA Signing询问的次数分别是：qH0，qH1，qH2，qH3，qE，qS，qPS，qPAS。

H0-queries：敌手A对随机预言机H0发起询问，算法为了响应询问，产生一个四元组（IDi，Qi，bi，ci）的列表L1。当敌手A对身份IDi询问H0时，算法 作如下响应：

1）如果IDi已经出现在列表L1中，则算法响应Qi=H0（IDi）。

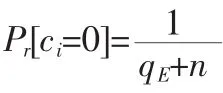
3）随机选择bi∈，如果ci=0，计算Qi=biY=bi（yP），如果ci=1，计算Qi=biP，并把四元组（IDi，Qi，bi，ci）添加到列表L1中，然后将Qi=H0（IDi）发送给敌手A。

H1-queries：C维护列表L2={Ppub，α，T}，当敌手A询问T值时，若记录存在，则返回T给A，否则，C随机选择α∈，计算T=αP，并将（Ppub，α，T）添加到列表L2中。

H2-queries：敌手A对随机预言机H2发起询问，算法为了响应询问，产生一个三元组（m，U，h）的列表L3。当敌手A对（m，U）询问H2时，算法作如下响应：

1）如果（m，U）已经存在于列表L3中，则响应H2（m‖U）=h。

H3-queries：敌手A对随机预言机H3发起询问，算法为了响应询问，产生一个五元组（IDi，mw，mi，Ri，di）的列表L4。当敌手A对（IDi，mw，mi，Ri）询问H3时，算法作如下响应：

1）如果（IDi，mw，mi，Ri）已经存在于列表L4中，则算法响应wi=di∈。

2）否则，随机选择ti∈，计算Ri=tiP，wi=H3（IDi‖mw‖mi‖Ri），并把（IDi，mw，mi，Ri，di）添加到列表L4中，并且响应wi=di∈。

Extraction queries:当敌手A询问身份为IDi的私钥时，算法 C作如下响应：运行H0-queries，查找列表 L1的四元组（IDi，Qi，bi，ci），如果ci=0，则算法输出“失败”，否则，计算Qi= biP，定义 dIDi=biPpub，注意到 dIDi=biX=bixP=xQi，因此 dIDi是身份IDi的私钥，并将dIDi发送给敌手A。

Signing queries:当敌手A询问身份为IDi的用户对消息mi的签名时，算法调出列表L1，如果ci=0，则算法输出“失败”，否则，表明Qi=biP。调出列表L3，如果（mi，Ui）已经存在于列表L3中，那么从中取得hi，否则，随机选择ri∈，计算Ui=riP，H2（mi‖Ui）=hi，并把（mi，Ui，hi）加入列表L3中。最后，计算Vi=riT+dIDihi，并把（Ui，Vi）发送给敌手A，则（Ui，Vi）就是消息mi在身份IDi下的一个有效签名。

Delegation queries:敌手A将授权证书mw，原始签名人身份ID0和代理签名人身份IDi（1≤i≤n）提交给算法，假设敌手A扮演的是原始签名人，则算法做如下响应：

1）在列表L1中，查找相应的（IDi，Qi，bi，ci），如果ci=0，则算法输出“失败”，否则，计算H（IDi）=biP，并将biPpub作为代理签名人IDi的私钥。

2）如果（mi，U0）已经在列表L3中，那么敌手A取得h0，否则，随机选择h0∈，并把（mi，U0，h0）加入列表L3，并计算V0= r0T+dID0h0。

3）运行PAGen算法，产生代理签名私钥xPi=V0+dID0h0。

PPA Signing queries：敌手A将授权证书mw，原始签名人身份ID0和代理签名人身份IDi（1≤i≤n）提交给算法，则算法按照代理权询问，产生代理签名人的代理私钥xPi=V0+ dIDih0，如果（IDi，mw，mi，Ri）已经存在于列表L4中，则响应wi=di∈Z，否则，随机选择ti∈，计算Ri=tiP，wi=H4（IDi‖mw‖mi‖Ri），并把（IDi，mw，mi，Ri，di）添加到列表L4中，响应wi=di∈。最后，计算签名Si=tiT+xPidi，则（mw，U0，Ri，Si）就是产生的部分代理签名。

PA signature queries:敌手A提交授权证书mw，原始签名人身份ID0和代理签名人身份IDi（1≤i≤n）以及消息（m1，m2，…，mn），算法运行代理权询问和部分代理签名询问产生各个代理签名人的部分签名（mw，U0，Ri，Si），生成代理聚合签名（mw，U0，Ri，S）。

最后，敌手A停止游戏，输出一个在n个消息-身份（mi，IDi）上的代理聚合签名（mw，U0，Ri，S），且在这n个消息-身份（mi，IDi）上至少存在一个（m1，ID1）没有经过私钥解析询问，当且仅当c1=0，c1=1（2≤i≤n），算法C没有失败退出，当c1=0有H1（ID1）=b1（yP），当ci=1（2≤i≤n），有H1（IDi）=biP。

如果敌手A扮演的是原始签名人，则由聚合签名满足的验证等式有

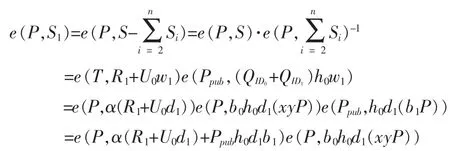
同理，如果敌手A扮演的是代理签名人，则由聚合签名满足的验证等式有

3.3 效率分析

将本文新方案的计算量与文献[11]和[12]进行比较，用Pr表示双线性对运算，Sm表示标量乘运算，n表示代理签名的用户数，则在代理聚合签名和验证阶段，文中新方案的计算量为3Pr+3nSm，而文献[11]的计算量为5Pr+3nSm，文献[12]的计算量3Pr+4nSm，由此可见，本文的新方案效率更高一些。

4 结束语

文中对一个基于身份的代理聚合签名方案进行了安全性分析，表明该方案不能抵抗签名伪造攻击，然后设计了一个新的可证安全的基于身份代理聚合签名方案，并且在随机预言模型下证明了新方案的安全性，和已有方案相比较，新方案的效率更高。基于身份的聚合签名方案的优点就是减少了签名验证的工作，解决了公钥证书的管理问题，在实际中我们进一步的工作就是设计可证安全的签名长度固定的无证书聚合签名方案。

[1]Mambo M，Usuda K，Okamoto E.Proxy signatures for delegating signing Operation[C]//Proceedings of the 3thACM Conference on Computer and Communications Security，ACM Press，1996:48-57.

[2]Shamir A.Identity-based cryptosystems and signature schemes[C]//Proceedings of Crypto 1984，LNCS 196，1984:47-53.

[3]Zhang F，Kim K.Efficient ID-based blind signature and proxy signature from bilinear pairings[C]//Proceedings of the 8th Australasian Conference on Information Security and Privacy.LNCS 2727，2003:312-323.

[4]Boneh D，Franklin M.Identity-based encryption from the Weil pairing[C]//Advances in Crypto 2001.LNCS 2139，2001:213-229.

[5]Xu J，Zhang Z，Feng D.ID-based aggregate signature from bilinear pairings[C]//Proceedings of the 4th International Conference on Cryptology and Network Security.Berlin:Springer-Verlag，2005，3810:110-119.

[6]Shim K A.An ID-Based aggregate signature scheme with constantpairingComputations[J].TheJournalofSystemsand Software，2010，83（10）:1873-1880.

[7]杜红珍，黄梅娟，温巧燕.高效的可证明安全的无证书聚合签名方案[J].电子学报，2013，41（1）：73-76.

[8]李艳文，杨庚.基于身份聚合签名方案的安全性分析与改进[J].计算机工程与应用，2012，48（28）：101-103.

[9]文毅玲，马建峰，王超.一个新的基于身份的聚合签名方案[J].计算机科学，2011，38（6）：54-57.

[10]彭延国，彭长根，冯蕾.一个基于证书的聚集签名方案[J].计算机科学，2011，38（12）:57-60.

[11]陈建能，岳昊，黄振杰.一个可证安全的基于证书聚合签名方案[J].计算机工程与应用，2013，49（21）：60-64.

[12]刘云方，左为平.高效的可证安全的基于证书聚合签名方案[J].计算机应用，2014，34（9）：2664-2667.

[13]孙华，郑雪峰，于义科，等.一种安全有效的基于身份的聚合签名方案[J].计算机科学，2010，37（5）：62-65.

[14]孙华，郭磊，郑雪峰，等.一种有效可证安全的基于身份代理聚合签名方案[J].计算机科学，2012，39（1）：44-52.

[15]王勇兵，卢晓杰，张建中.一种基于身份的代理聚合签名方案[J].济南大学学报，2012，25（3）：301-304.

Provably secure identity-based proxy aggregate signature scheme

HU Jiang-hong
（College of Mathematics and Information Science，Baoji University of Arts and Sciences，Baoji 721013，China）

Through secure analysis of an identity-based proxy aggregate signature scheme，this paper proved the aggregate signature couldn't resist forgery attack.Based on the scheme，this paper proposed a new identity-based proxy aggregate signature scheme with the bilinear pairings，and proved the proposed scheme is secure against existential forgery attack under the computational Diffie-Hellman problem in the random oracle model.The new scheme only needs three pairing computation in the verification stage and is more efficient than the known schemes.

proxy aggregate signature；identity-based signature；bilinear pairing；Diffie-Hellman problem

TN918

A

1674－6236（2016）18-0010-03

2016-02-25 稿件编号：201602134

国家自然科学基金（61402015）；陕西省教育厅专项科研计划项目（15JK1022）；宝鸡市科技计划项目（14GYGG-4-2, 15RKX-1-5-8）；宝鸡文理学院一般项目（YK1618）

胡江红(1981—)，女，陕西宝鸡人，硕士,讲师。研究方向：密码学与信息安全。