从一次错误解题谈问题解决的普适性

☉浙江省上虞中学　王立东

从一次错误解题谈问题解决的普适性

☉浙江省上虞中学王立东

众所周知，数学问题对学生而言能够记忆最为深刻的是发生在学生身上的错误.常常有毕业的学生这样与笔者交流：以前老师给我讲的这个错误的问题，我记的很牢，一直没有再犯.从魏书生教育故事中也这样描述过：“学生因为数学问题错误的分析，研究出了一系列相关的结论和成果.”在这个教育故事中，笔者认识到了从错误解题发现闪光点所在的一系列错题教学设计方式方法，第一是研究学生错解原因，分析学生问题错因的普遍性所在；第二是教学设计相关类似问题进行深度和广度上的研究，主要以变式教学的设计进行教学载体，让问题的普遍性得到渗透.

问题：已知f（x）=ax2+cx，且1≤f（1）≤3，-1≤f（-1）≤1，求f（2）的取值范围.（不等式性质作业题）

设计意图：虽然简单线性规划问题的常规通法是“图解法”，即寻找线性约束条件、线性目标函数，然后由二元一次不等式（组）表示的平面区域作出可行域，最后在可行域内求目标函数的最优解，但由于学生作图的熟练程度不够，此类问题又常出现在选择填空中，学生总会另辟蹊径寻求更简单的解决方法，因此常出现如：不等式之间通过性质化简至一元一次不等式后代入目标函数求最值、解对应约束条件的方程组得可行域顶点坐标后代入求目标函数最值等偶有成功的方法，且津津乐道，却不深入思考这些方法的普适性，导致解题常误入陷阱.“错误是最好的学习资源”，本课时就针对此现象，利用图解法，直观地将一系列变式题进行显性解析，让学生能够辨明解题误区，充分认识到数形结合图解法的优势所在，在平时的学习中能够扎实基础，提高作图、识图、用图的能力，攻克线性规划问题.

分析：本题属于新视角看旧问题，给出曾在“不等式性质”教学时出现的一个求范围问题，通过“示错”引出思考——不等式条件如何应用才能保证其等价性，再从线性规划的角度，直观地用可行域展现不等式组所对应的约束条件，尝试让学生更好地理解不等条件等价转换的重要性，强调“数形结合思想”在此起到的直观转化的关键作用.

①+②，得0≤2x≤4，即0≤4x≤8.

②×（-1），得-1≤y-x≤1③.

①+③，得0≤2y≤4，故而代入f（2）=4x+2y，得0≤f（2）≤12.

正解：f（2）=4x+2y=3f（1）+f（-1），由已知可得，3≤3f（1）≤9，-1≤f（-1）≤1，故而两式相加可得2≤f（2）≤10.

辨析说明：分别将题设不等式条件与错解中转换得到的不等式条件用可行域的方式呈现，即可看到二者并不等价，因此通过不等式进行运算将二元一次不等式转化为一元一次不等式实质上是放宽了题设条件，忽略了x、y之间的制约关系，而作出可行域则完全展现了约束条件的全貌.为后续环节进一步利用“数形结合思想”辨析各种错误理解做铺垫.

图2　

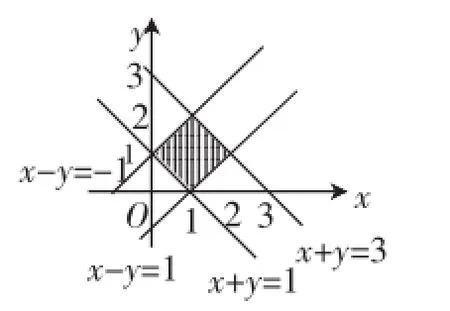
图1　

变式1：已知点P（x，y）所在区域D满足条件求z=2x+y的最值.

设计意图：经验之谈与解题规律的碰撞设计.学生在解决线性规划问题时常常发现目标函数的最值往往在可行域的顶点处取到，进而在解题时，为图方便或节约时间，就简单地处理成“求边界线交点坐标，代入目标函数，比较大小，求出最值”.本环节通过一个基本问题的几个变式，让学生看到以上的经验之谈不能作为解题规律通行应用，而数形结合，在可行域中利用目标函数的几何意义来解题才是通法，以此来促进学生在平时的学习过程中学会反思和自查.

解析：z=2x+y⇒y=-2x+ z，作可行域如图3所示，由图可知，在点B（1，1）处，z取得最小值3，在点C（5，2）处，z取得最大值12.

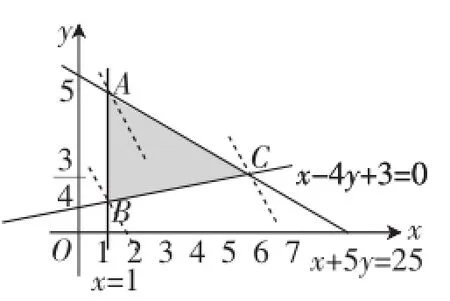
图3　

此题目标函数的最值是在可行域的顶点处取到的.

分析：若不作图，仅求顶点处目标函数来求取值范围，看似没有问题，但实质上取得的最大值的最优解是有无数多个的，在实际应用为背景的线性规划问题中，往往希望求的是如何取得最值的执行方案，也就是最优解，因此必须注重过程而不能只注重结果.

变式3：已知点P（x，y）所在区域D满足条件

求z=2x+y的最值.

分析：此题仅改变一个不等式符号，可行域发生了变化，虽与上题有相同的目标函数，但边界线的交点已不能都落在可行域中，按上题解法则会在取最小值时出错，而且此题开放的可行域，最大值也是取不到的.

解：z=2x+y⇒y=-2x+z，作出可行域如图4所示.所以在点A处，z取得最小值无最大值.

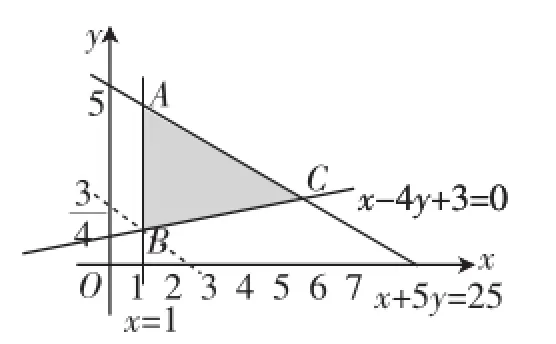
图4　

分析：此题添加了整点条件，学生在解题时容易忽视该条件而造成错误，根本原因就是画可行域后只关注可行域顶点的惯性思维.

解：z=2x+y⇒y=-2x+z，可行域如图5中的整点.由x∈N*，y∈N*，可得在点附近，x=1时，⇒y≥5，所以z在点（1，5）处取得最小值7.

辨析说明：通过四个变式，希望能够使学生注意到惯性思维容易引入误区，而数形结合，作出可行域，运用图解法，才是通性通法.

变式5：已知点P（x，y）所在区域D满足条件求下列目标函数的取值范围：（1）z=|x+y-示点P（x，y）到直线l：x+y-3=0的距离，由图6可知，点P在直线l上，则zmin=0，点P在点C（5，2）处，则zmax= 4，故z∈［0，4］.

设计意图：目标函数除了常见的二元一次函数，有时目标函数可能是非线性的，那么如果能够充分利用其几何意义，然后结合图解法，便可以结合解析几何知识来加以解决.这种非线性目标函数成为线性规划问题更为普遍的考查.

解析：（1）令d=

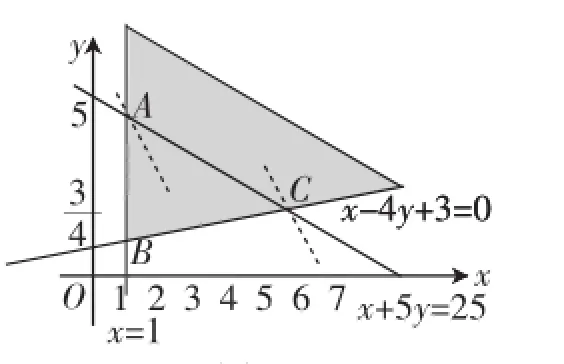
图5　

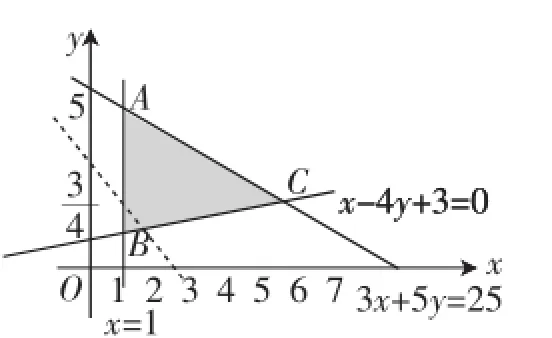
图6　

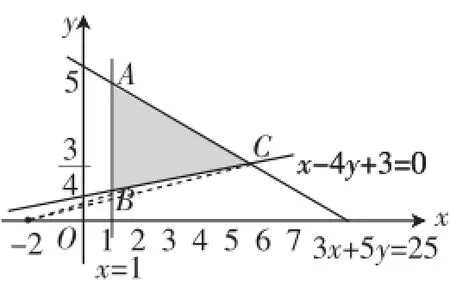
图7　

min

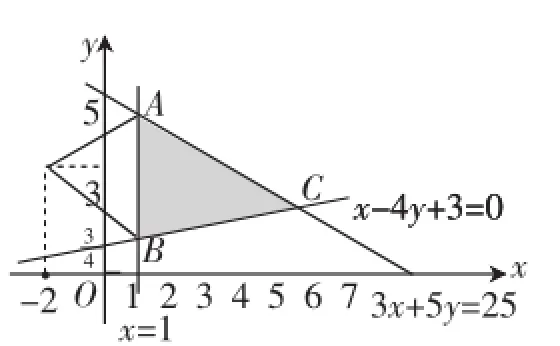
图8　

辨析说明：通过这三个小题，希望学生能够认识到简单的线性规划问题，它的图解法的本质就是把问题化归到解析几何范畴，利用解析几何知识来求解，因此，学习过程中必须要有联系地看问题.

小结：

（1）可行域的作图必须规范准确，勤练基本功，不能畏难怕繁；

（2）要深刻理解：“线性规划”问题就是把代数问题用数形结合思想转化为解析几何问题的本质；

（3）平时学习要有联系、系统性地看待数学知识之间的关联与作用，这样才能由点及面，提高学习效率.

从上述教师设计的从学生错题研究到变式的深入挖掘和广度拓展，笔者发现学生对于线性规划问题的一系列深度、广度问题的学习有了系统性的、体系性的掌握.这种学习是一类问题研究的普适性方式方法，很值得教学中对于典型错误问题的研究.通过学习和实践，笔者认为应该做好这些准备工作以便得到类似问题解决的普适性：其一，选择合理的学生较为容易犯错的典型问题为载体，选择比较常见的错解为背景剖析；其二，对于问题解决切勿只是就题论题，这样的方式往往比较单一，不具备以点及面的效果，不利于课堂教学的有效和高效，因此选择错题背景下的变式探索是一种有效化的手段，本文以常见线性规划问题辅助，将知识间整合起来，有效地回答了学生错解的缘由和为什么线性规划知识解决的正确性；其三，将这样的教学思路开拓至更多的教学内容中，则有效地提高了学生数学知识运用的正确性，更整合了知识间的层次，大大地提升了数学课堂教学效率.

1.宋卫东.从生“动”到生动，诠释思维品质的提升［J］.中学数学月刊，2013（5）.

2.方厚石.向量教学诠释思维品质［J］.数学通讯，2014（1）.

3.沈恒.浅谈中学数学课堂教学的适度形式化［J］.中小学数学，2010（5）.F