以圆锥曲线为例谈解题教学的几点感悟
2016-11-25江苏省如皋市搬经中学章杰
☉江苏省如皋市搬经中学 章杰
以圆锥曲线为例谈解题教学的几点感悟
☉江苏省如皋市搬经中学章杰
在教学中,教师应该教会学生从观察、思考、联想、变换思考角度等方面去分析问题,进而确定解题的思路和方法.学生也应该养成良好的学习品质,勇敢地面对遇到的任何困难,树立战胜困难的信心和决心.在我们的思维处于困境的时候,从条件的特定含义分析和解决问题,是解决数学难题的一种有效途径.下面以圆锥曲线问题为例,来谈谈笔者在解题教学中的几点感悟.
一、审题如沙里淘金,是金子总要发光
审题是解题的基础,思维受阻往往是对条件没有进行仔细观察和思考,忽视了某些条件的重要作用,没有转化分解能力的差异.审题如同沙里淘金,不要漏掉任何一个线索,一个不起眼的条件或许就能打开成功的大门.
(1)求a,b的值;
(2)求证:直线MN的斜率为定值.
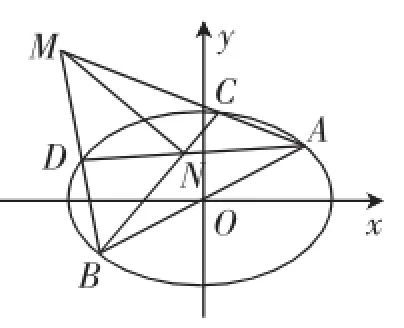
图1
解析:(1)设点A(x1,y1),则B(-x1,-y1).由已知得解得x1=2,y1=1,代入椭圆方程,再结合离心率为,求得a=
(2)对于此问,题目给出的条件不少,但是值得我们关注的是“直线l:y=与椭圆E相交于A、B两点”,这个条件等价于“A、B两点关于原点对称”.对于CA、CB、DA、DB中,假设斜率存在时,我们进一步地挖掘可以得到设CA的斜率为k1,DA的斜率为k2,可得到这样一来,直线AD的方程为y-1=k2(x-2),直线BC的方程为y+1=-求点N
上述问题,虽然给出的条件众多,但是问题的突破口应该是
二、突破思维受阻是对心理素质的考验
数学问题的解决经常伴随着困难、挫折和失败.有些学生在思维受阻时,冥思苦想,不肯放弃原有思路,钻牛角尖,固执己见,当然是穷途末路苦徘徊,到头来一无所获.也有人碰到难题,急于求成,一旦思路受阻,找不到切入点,就会烦躁不安,心慌意乱.也有人遇到思维受阻,能够冷静地观察,善于寻找特定条件的微妙含义,迅速转换思维角度,灵感突现,这种成功的快感难以言表.
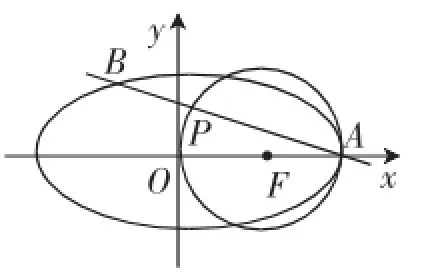
图2
(1)求椭圆C和圆F的方程;
(2)已知过点A的直线l与椭圆C交于一点B,与圆F交于另一点P.请判断是否存在斜率不为0的直线l,使P恰好为线段AB的中点?若存在,求出直线l的方程;若不存在,说明理由.
(2)对于本问的求解,大部分学生的思路是:设出直线AB的方程,与椭圆方程联立,利用中点坐标公式表示出点P坐标,再由点P在圆F上,故点P的坐标满足圆的方程.再利用此关系判断满足条件的直线是否存在.
设B(x1,y1),则2+x1=可得中点P由点P在圆F上可得化简整理得k2=0.又因为k≠0,所以不存在满足条件的直线l.
解析几何既具有几何特征,又具有代数性质.几何问题代数化是处理解析几何问题的常用策略,解题中要善于挖掘隐藏的平面几何属性,为代数化创造条件.代数化的过程既可以将几何问题直接代数化,也可以先把几何问题利用几何方法进行适度简化,再代数化.通常前者思维量小但计算量大;后者计算量小但思维量大.
三、灵感依赖于对条件的点滴探索
在解题中,当遇到一道难题时,某些同学对题发呆,虽然绞尽脑汁,灵感也总是出不来,自己着急,老师也替学生发急.其实题目中的每个条件都具有自己的特定含义,我们不妨把它们转化一下,哪怕是一小步,写一写、化一化、算一算,也许在写与算的过程中就可以得到一些启发.
例3如图3,在平面直角坐标系中,已知抛物线y2= 2px(p>0),设点D(n,0),E(m,0),M为抛物线上的动点(异于顶点),连接ME并延长交抛物线于点N,连接MD、ND并延长交抛物线于点P、Q,连接PQ,设直线MN、PQ的斜率存在且分别为k1、k2.
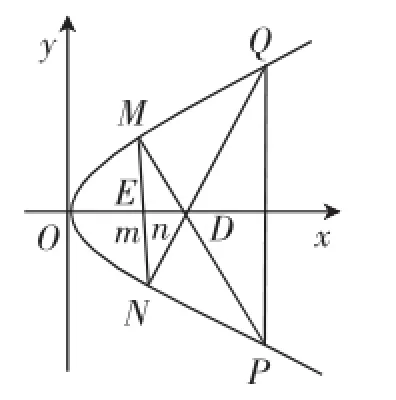
图3
(1)若k1=1,m=2,|MN|=4求p;
(2)是否存在与p无关的常数λ,使得k1=λk2恒成立,若存在,请将λ用m、n表示出来;若不存在,请说明理由.
解析:(1)略.
(2)本题条件众多,容易分散我们的注意力.抛物线居然有四个点M、N、P、Q,其中M、E、N三点共线,M、D、P三点共线,N、D、Q三点共线,直线MN、PQ的斜率分别为k1、k2.如果想k1=λk2恒成立时λ的值存在,那么这么多的条件,从哪个地方下手,设点还是设直线,乍一看肯定是心慌意乱的.
其实虽然有这么多点的共线,但是它们的性质特征应该是一致的,任何三点共线具有的性质应该是相似的,其实这也是他们的突破点,如果我们能够行动起来,集中攻击这个弱点,在计算过程中还可能获得启发,进而乘胜推进,最终获得成功.基于此,我们不妨从M、E、N三点共线入手,设M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4),得由于M、N是抛物线上的点,可以化简再化简得,y2y1= -2pm.这是多么惊喜的战果呀!也就是说,从M、E、N三点共线可以得到y2y1=-2pm,那么可以肯定地说,从M、D、P三点可以得到y3y1=-2pn,从N、D、Q三点共线可以得到上式巩固阵地,即,需要将y3、y4替换成y1、y2,则k2=再来看等式存在.因此,存在与p无关的常数λ=,使得k1=λk2恒成立.
综上,对于解析几何问题,一般来说解题过程都比较烦琐,运算量较大,如何简化运算就成了同学们迫切要解决的问题,因此在教学过程要注重培养学生综合运用所学知识解决问题的能力;要加强学生运算、转化能力的强化训练;要注意问题的求解中分类讨论、数形结合、函数不等式、参数法等数学思想方法的渗透.F
