巧用余弦定理求解一类圆锥曲线高考题

☉浙江省临海市台州中学　毕里兵

巧用余弦定理求解一类圆锥曲线高考题

☉浙江省临海市台州中学毕里兵

近日，笔者在办公室和同事参与讨论了一个圆锥曲线问题.

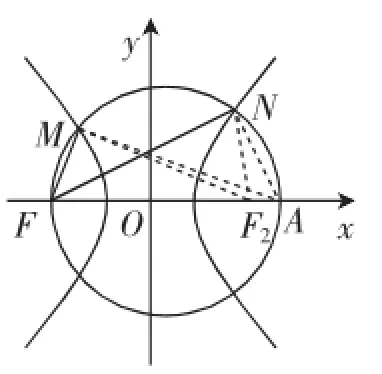
图1　

经过激烈的讨论，大致得出三种方法：特殊化法（不妨设点A为双曲线的右焦点）、向量法、余弦定理法，现把余弦定理法过程记录如下.

解：如图1所示，记双曲线的右焦点为F2，并设FM=x，FN=y，FA=z.

则MF2=8+x，NF2=y-8，AF2=z-10

同理可得

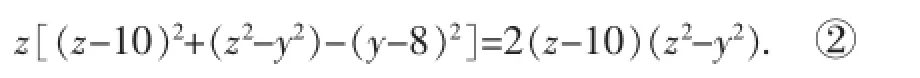
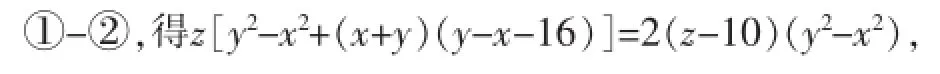
这种利用余弦定理求解的思路勾起了笔者对一类圆锥曲线高考题解法的思索.笔者下面以近几年的几道高考题为例，谈谈余弦定理在优化圆锥曲线运算方面的应用.现分析如下，供大家参考.

例1（2014年高考全国卷Ⅱ理科第20题）设F1，F2分别是椭圆C：的左，右焦点，M是C上一点且MF2与x轴垂直，直线MF1与C的另一个交点为N.

（1）若直线MN的斜率为，求C的离心率；

（2）若直线MN在y轴上的截距为2，且|MN|=5|F1N|，求a，b.

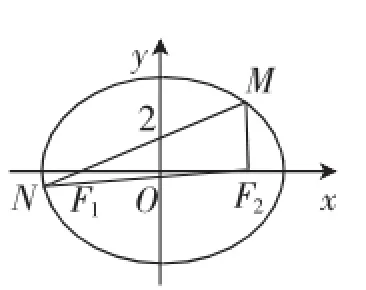
图2　

（2）如图2所示，由题意，原点O为F1F2的中点，MF2∥y轴，

所以直线MF1与y轴的交点（0，2）是线段MF1的中点，故|MF2|=

设|NF1|=t

在△NF1F2中，由余弦定理得

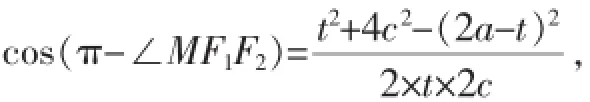
说明：解决这类问题的关键是对焦点弦的处理，一般是设出某一线段长度，然后结合圆锥曲线定义表示出焦点三角形其余的边长，最后选用一个合适的角度，应用余弦定理列出表达式，就可以简捷地求解.

例2（2014年高考安徽卷文科第21题）设F1，F2分别是椭圆E：的左、右焦点，过点F1的直线交椭圆E于A，B两点，|AF1|=3|BF1|.

（1）若|AB|=4，△ABF2的周长为16，求|AF2|；

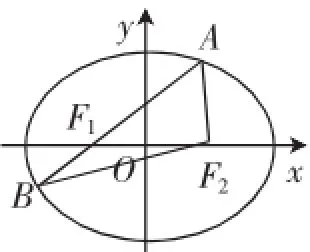
图3　

解：（1）|AF2|=5.（过程略）

（2）如图3所示，设|F1B|=t（t＞0），则|AF1|=3t，|AB|=4t，由椭圆定义可得|AF2|=2a-3t，|BF2|=2a-t.

在△ABF2中，由余弦定理可知，|AB|2=|AF2|2+|BF2|2-2|AF2|·|BF2|· cos∠AF2B，

化简可得（a+t）·（a-3t）=0，解得a=3t.

于是有|AF2|=3t=|AF1|，|BF2|=5t，

所以|BF2|2=|AF2|2+|AB|2，可得AF1⊥AF2.

故△AF1F2是等腰直角三角形，从而2a2=4c2，

（1）求a，b；

（2）设过F2的直线l与C的左、右两支分别相交于A，B两点，且|AF1|=|BF1|，证明：|AF2|，|AB|，|BF2|成等比数列.

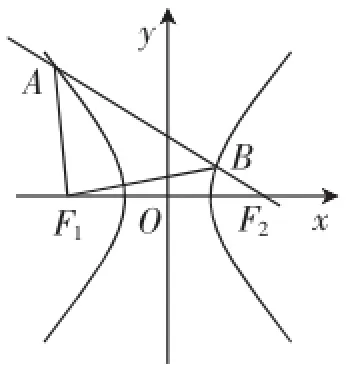
图4　

如图4所示，设|BF2|=t，则由双曲线定义知，|BF1|=2a+t=2+t，

所以|AF1|=|BF1|=2+t，|AF2|=4+t，从而|AB|=|AF2|-|BF2|=4.

在△BF1F2，由余弦定理得cos∠F1BF2=

在△BAF1，由余弦定理得cos（π-∠F1BF2）=，即cos

所以|AF2|·|BF2|=t（4+t）=t2+4t=16=|AB|2，所以|AF2|，|AB|，|BF2|成等比数列.

例4（2012年高考安徽卷文科第20题）如图5所示，F1，F2分别是椭圆的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C的另一个交点，∠F1AF2=60°.

（1）求椭圆C的离心率；

（2）已知△AF1B面积为40，求a，b的值.

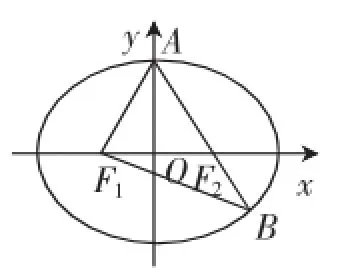
图5　

（2）设|BF2|=t，则|BF1|=2a-t，

在△BF1F2中，由余弦定理得|BF1|2=|BF2|2+|F1F2|2-2|BF2|×|F1F2|×cos120°，

例5（2010年高考新课标卷理科第20题）设F1，F2分别是椭圆E：=1（a＞b＞0）的左、右焦点，过F1斜率为1的直线l与E相交于A，B两点，且|AF2|，|AB|，|BF2|成等差数列.

（1）求E的离心率；

（2）设点P（0，-1）满足|PA|=|PB|，求E的方程.

解：（1）如图6所示，由椭圆定义知，|AF2|+|BF2|+|AB|=4a，

又2|AB|=|AF2|+|BF2|，得|AB|=

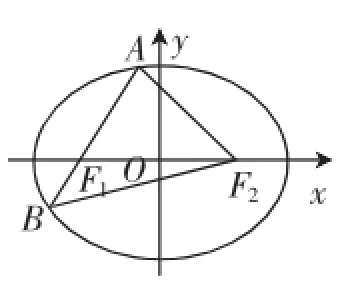
图6　

由题意直线l的倾斜角为45°，可得∠AF1F2=45°，∠BF1F2=135°，

设|AF1|=t，|BF1|=m，则|AF2|=2a-t，|BF2|=2a-m，

在△AF1F2中，由余弦定理得

（2a-t）2=4c2+t2-4tccos45°，得t=

在△BF1F2中，由余弦定理得

（2a-m）2=4c2+m2-4mccos135°，得m=

（2）设AB的中点为N（x0，y0），由（1）可知，|AF1|=t=a，|BF|=a，b=c，1

所以e=

说明：上述几道试题相关的焦点三角形在图形中都能直观的观察到，但是有一类试题是属于隐藏型的，这时我们只要根据圆锥曲线的特点把它补充出来即可.

例6（2010年高考辽宁卷理科第20题）设椭圆C：

（1）求椭圆C的离心率；

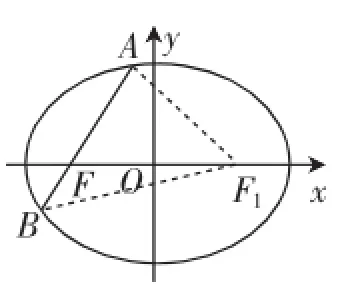
图7　

解：（1）如图7所示，记F1为椭圆的右焦点，连接AF1，BF1.由题意可得∠AFF1=60°，∠BFF1=120°，由椭圆定义知|BF1|+|BF|=|AF1|+|AF|=2a，设|BF|=t，则|BF1|=2a-t，|AF|=2t.

在△BFF1中，由余弦定理得

（2a-t）2=4c2+t2-4tccos120°，

在△AFF1中，同理可得所以（2）把③代入②得t=所以|AB|=3t=所以c=2，

例7（2011年高考浙江卷理科第17题）设F1，F2分别

解：如图8所示，延长AF1交椭圆于B′，则根据椭圆对称性知所以|AF1|=5|F1B′|.

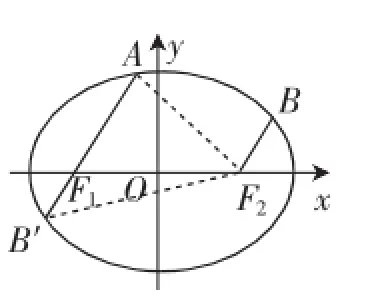
图8　

连接AF2，B′F2，并设|F1B′|=t，

则|AF1|=5t，|AF2|=2a-5t，|B′F2|= 2a-t.

在△AF1F2中，由余弦定理得cos∠AF1F2=

在△B′F1F2中，由余弦定理得cos（π-∠AF1F2）=

所以|AF1|=5t=

则点A为椭圆的顶点，故点A坐标为（0，1）或（0，-1）.

高考试题是许多专家、学者、优秀教师集体智慧的结晶，具有很高的研究价值.研究高考试题是高中教师的必修课，最大限度地发挥高考试题的指导价值是这门功课的重中之重.波利亚说：“没有一道题是解决得十全十美的，总剩下一些工作要做，经过充分的探讨总结，总会有点滴的发现，总能改进这个解答，而且在任何情况下，我们都能提高自己对这个解答的理解水平.”这告诉我们教师，在平时的课堂教学中，不仅要得到问题的答案，还要让学生知道问题的一般规律，这样才能使学生举一反三，触类旁通，以不变应万变.Y