蒙日圆以及应用*

☉福建省厦门第一中学　王淼生

☉福建省厦门第一中学　黄昌毅

蒙日圆以及应用*

☉福建省厦门第一中学王淼生

☉福建省厦门第一中学黄昌毅

小学开始接触圆，初中学习圆并掌握圆的基本性质，但初中侧重从图形（几何法）上理解圆即定性研究.进入高中，在直角坐标系中即用坐标（代数法）来定量研究并得到圆的标准方程及一般方程.定性与定量有机结合、数与形完美互补，使得对圆的研究达到较为完善的程度.其实，圆有更多丰富内涵，比如阿波罗尼斯圆、蒙日圆，等等.然而不少数学教师对此并不熟悉，甚至根本不知道.本文浅谈蒙日圆相关定理、证明及应用，以求抛砖引玉.

一、蒙日圆概念

在椭圆中，任意两条互相垂直的切线的交点都在同一个圆上，它的圆心是椭圆中心，半径等于长、短半轴平方和的算数平方根，这个圆就是蒙日圆.用符号语言表示为：

我们知道圆锥曲线具有“家族”现象，即可将椭圆具有的性质类比到双曲线，不难得到：

其实，从伸缩变换的角度，我们可以将圆视为特殊的椭圆，从而得到：

定理3过圆x2+y2=a2（a＞0）上任意不同两点A、B作圆的切线，若切线垂直且相交于P，则动点P的轨迹为圆x2+y2=2a2.

出于追求外形结构一致性，我们也可以将上述定理3叙述为：

站在复数的高度，我们还可以这样描述上述定理2：

数学是有趣的又是神奇的.基于上述探索，为了体现圆锥曲线的统一美、形式美、理性美及和谐美，我们可以将上述定理1、定理2及定理3统一归纳为：

上述研究表明圆锥曲线“家族”具有“遗传性”.从生物学来说，有遗传必有变异！正是因为变异，导致抛物线出现突变.由于抛物线只有一个焦点，因此我们可以设想另一个焦点在无穷远处，于是就可以把直线视为半径为无穷大的圆，由此可以得到：

定理4过抛物线y2=2px（p＞0）上任意不同两点A、B作抛物线的切线，若切线垂直且相交于P，则动点P的轨迹为准线x=

二、证明上述定理

上述定理3、定理4的证明较为简单，请读者自行推理.以下证明定理1、定理2.为了得到定理1、定理2的简捷证法，我们先介绍一个引理.

1.引理

我们知道解析几何综合问题突出特点就是入手不难、入口较宽，但运算量大、推理复杂，导致很多学生不得不中途放弃而前功尽弃，令人扼腕叹息.其实何止是学生！惭愧的是笔者自己在文［1］中也是采取代数推理的方法证明了上述定理1、定理2.代数论证固然严谨，但计算复杂、过程冗长，这就促使笔者寻觅新的简捷方法.经探究获得以下引理：

引理O为矩形ABCD所在平面上任意一点，则有OA2+OC2=OB2+OD2.

上述引理的证明较为简单，直接利用勾股定理、或建系、或借助向量都可以完成，请读者自行推理.以下利用上述引理并借助椭圆及双曲线的光学特性来论证上述定理1、定理2即证明蒙日圆.

2.证明定理1

证明：如图1所示，设F1，F2为椭圆的左、右焦点，过F1作关于PA的对称点M，且与PA相交于G，由椭圆光学性质可得三点M、A、F2共线，依据椭圆定义可得

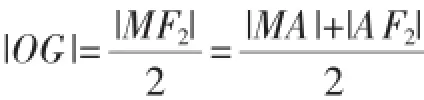
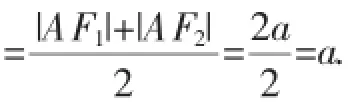
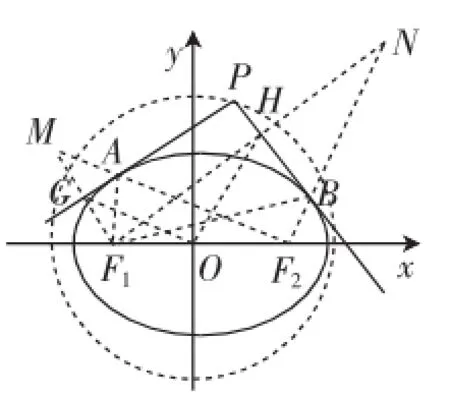
图1　

过F1作关于PB的对称点N，且与PB相交于H.同理可得|OH|=a.由图1及题意可知四边形F1GPH为矩形，依据上述引理可得OG2+OH2=OF12+OP2⇒a2+a2=c2+OP2⇒OP2= a2+b2.

故动点P轨迹方程为x2+y2=a2+b2.

3.证明定理2

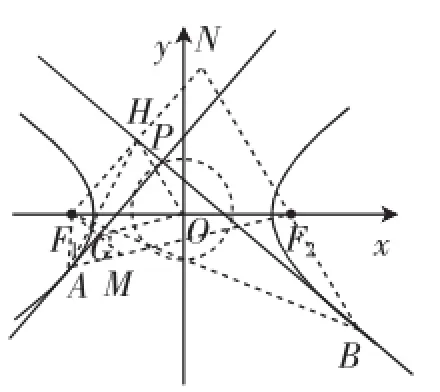
图2　

证明：如图2所示，设F1，F2为双曲线的左、右焦点，过F1作关于PA的对称点M，且与PA相交于G，由双曲线光学性质可得三点M、A、F2共线，依据双曲线定义可得

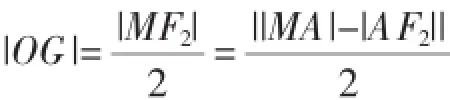
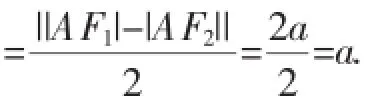
过F1作关于PB的对称点N，且与PB相交于H.同理可得|OH|=a.由图2及题意可知四边形F1GPH为矩形，依据上述引理可得

OG2+OH2=OF12+OP2⇒a2+a2=c2+OP2⇒OP2=a2-b2.

故动点P轨迹方程为x2+y2=a2-b2.

三、进一步探究蒙日圆

事实上，经探究发现上述四个定理的逆命题也成立，由此分别得到

定理5过圆x2+y2=a2+b2上任意点P作椭圆（a＞b＞0）的两条切线，则两条切线垂直.

定理6过圆x2+y2=a2-b2（a＞b＞0）上任意点P作双曲线的两条切线，则两条切线垂直.

定理7过圆x2+y2=2a2上任意点P作圆x2+y2=a2的两条切线，则两条切线垂直.

请读者模仿上述定理1、定理2的证明方法自行推理上述定理5～8.

四、蒙日圆的精彩应用

依据上述定理1～定理8可以命制出许许多多高质、优雅的与蒙日圆相关的试题.请看以下案例：

案例1已知圆O：x2+y2=1，若直线y=kx+2上总存在点P，使得过点P作圆O的两条切线相互垂直，则实数k的取值范围是______________.

（Ⅰ）求椭圆C的标准方程；

（Ⅱ）若动点P（x0，y0）为椭圆C外一点，且点P到椭圆C的两条切线相互垂直，求点P的轨迹方程.

案例3已知圆O：x2+y2=34，椭圆C：

（Ⅰ）若点P在圆O上，线段OP的垂直平分线经过椭圆的右焦点，求点P的横坐标.

（Ⅱ）现有如下真命题：

“过圆x2+y2=52+32上任意一点Q（m，n）作椭圆=1的两条切线，则这两条切线垂直”；

“过圆x2+y2=42+72上任意一点Q（m，n）作椭圆=1的两条切线，则这两条切线垂直”.

据此，写出一般结论，并加以证明.

评注：上述案例1是我校2015届高三模拟试题，不少学生束手无策，得分率极低.其实由定理3可得点P轨迹方程为x2+y2=2.由于点P又在直线y=kx+2上，即点P既在圆又在直线上，也就是说直线与圆恒有公共点，即直线与圆相切或相交，依据点到直线间的距离d≤r可得k≥1或k≤-1.案例2是2014年高考广东省理科试题第20题.案例3是2013年厦门市高三质检第22题（压轴题）.显然案例2是依据蒙日圆概念即上述定理1而命制；案例3源自蒙日圆逆定理即上述定理5而得到.可以预言这样的试题会不断涌现，倘若在高三总复习中实施“集团作战”，集中“火力”短、平、快地一次性彻底解决与蒙日圆相关的这一类问题，必然会收到很好的效果，这一点已经得到越来越多的教师、专家的认可（如拙文［2］）.笔者曾经做过一次问卷调查，统计结果表明学生特别喜欢这种教学策略与模式，尤其是涉及解析几何综合问题更是受到高三学子们的青睐.

1.王淼生.从一道哈佛试题浅谈因数构形策略［J］.中学数学（上），2015（7）.

2.王淼生.由一道质检题得到一组有趣的结论［J］.福建中学数学，2013（10）.

3.王淼生.攻克解几试题的策略——组团、抱团［J］.中小学数学（高中版），2014（5）.

4.王淼生.透过现象追根溯源看清本质［J］.中学数学（上），2015（12）.Y

*注：本文是福建省“十二五”规划2013年度课题“优化学生思维品质的魅力数学课堂模式研究”（立项批准号：FJJKXB13-083）的阶段性成果.