解析几何最值的计算需要增加的一节专题课

☉江苏省张家港市乐余高级中学　张士亮

解析几何最值的计算需要增加的一节专题课

☉江苏省张家港市乐余高级中学张士亮

求动点到两定点距离的和与差的最值问题，由于定点处于轨迹的异侧与同侧，轨迹是直线与曲线、距离是和与差的不同而不同，解决策略灵活多变.笔者在教学实践中却发现，这些问题其实具有共同的性质和解题策略，都可以采用“同侧差最大，异侧和最小”的统一思想方法轻松解决.因此，笔者认为有必要在高三解析几何复习中对此类问题进行系统归纳和深入探究，以便让学生能够站得更高、看得更远，在高观点下求解此类问题.笔者对此类的探究如下，仅供参考.

一、问题情境

自从学习平面几何后，我们就知道“两点之间，线段最短”这个原理.其最典型的应用就是求最短路径问题.如下面的两个问题.

问题1：位于公路a两侧的两所学校S、T，若要在公路上设立一个公交车站B，使两所学校到该车站的距离之和最小，试设计车站的位置，并说明理由.

探究：问题特征——定点S、T位于动点的运动轨道的异侧，可求距离之和的最小值.简单地说，就是“异侧和最小”.解决这种最值的基本原理——两点之间，线段最短.证明过程实质上是借助三角形两边之和大于第三边来解决.

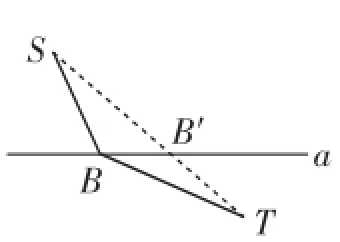
图1　

解：如图1，连接ST，线段ST与直线a的交点是B′，在直线a上任取一点B，SB+TB≥ST，当且仅当点B与B′重合时有SB′+TB′=ST，所以SB+TB的最小值也就是线段ST的长度.

问题2：位于公路a同侧的两所学校S、T，若要在公路上设立一个公交车站B，使两所学校到该车站的距离之差SB-TB最大，试求出车站的位置，并说明理由.

探究：问题特征——定点S、T位于动点的运动轨道的同侧，可求距离之差的最大值.简单地说，就是“同侧差最大”.

解：连接ST并延长交直线a于点B′，如图2所示，在直线a上任取一点B，根据“三角形两边之差小于第三边”的原理可知SB-TB≤ST，当且仅当点B与B′重合时有SB-TB=ST，所以SB-TB的最大值是ST的长度.

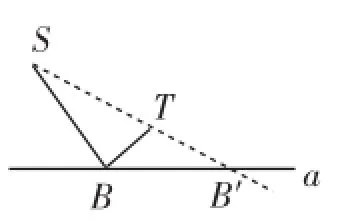
图2　

二、“定理”建构

综上所述，探究活动所研究的问题其实质是平面几何中的两个最简单的最值问题，包含两个最简单的道理：

（1）当定点S、T位于动点运动轨道的异侧时，可求动点与两定点距离之和的最小值，连接ST与轨道的交点可得点B，即为所求；

（2）当定点S、T位于动点运动轨道的同侧时，可求动点与两定点距离之差的最大值，延长线段ST或TS与轨道交点为B，即为所求.

正如我们在学习基本不等式时遇到的最值定理：“积定和最小”，“和定积最大”，这里我们也可以概括出一个重要的结论：“异侧和最小”，“同侧差最大”.

值得注意的是，这个结论仅仅为大家提供了一种解题思想方法，一种思考转化的方向指引，而不是直接给出了一个结论，在利用和理解定理时一定要弄清楚定理证明的原理及最值的概念，因为它们基本上都可以归纳成三角形三边不等关系，同时作为最值，首先应该是在某种情形下，可以取到这个值，才能称之为最值.

三、模型应用

在定直线上求动点P到两个定点距离之和的最小值或最大值问题，这里动点的运动轨迹不仅仅是直线，也可以是曲线.如圆、椭圆、双曲线、抛物线等.

1.在圆中的应用

例1已知圆C1：（x-2）2+（y-3）2=1，圆C2：（x-3）2+（y-4）2=9，M、N分别是圆C1、C2上的动点，P为x轴上的动点，则|PM|+|PN|的最小值为_________.

分析：由于三个点P、M、N均为动点，但是当点P静止时，可以看出线段PM、PN的大小之间没有直接关联.因此若求|PM|+|PN|的最小值，只需要PM与PN都达到最小，而且这是可以实现的.

解：假设P点位置如图3，则|PM|min=PC1-1，|PN|min=PC2-3，|PM|+|PN|≥PC1+PC2+4，取C1（2，3）关于x轴的对称点C1′（2，-3），当且仅当C1′、P、C2三点共线时距离之和最小，|PM|+

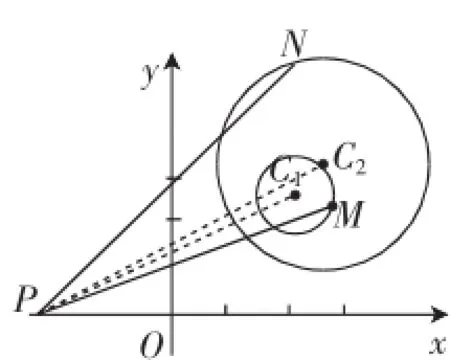
图3　

变式：已知圆C1：x2+（y-4）2=4，圆C2：（x-9）2+y2=1，M、N分别是圆C1、C2上的动点，P为y=x上的动点，则|PN|-|PM|的最大值为_________.

解析：假设P点在直线y=x上不动，则|PM|min=PC1-2，|PN|max=PC2+1，|PN|-|PM|≥PC2+1-PC1+2=PC2-PC1+3，取C1（0，2）关于y=x的对称点C1′（2，0），连接C1′C2并延长交y=x于点O，因为PC2-PC1′≤C2C1′=1，所以PC1′-PC2≥1.

2.在椭圆中的应用

例2设F1、F2分别是椭圆的左、右焦点，P为椭圆上任一点，点A的坐标为（6，4），则PA+PF1的最小值为_________.

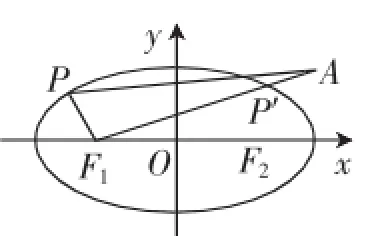
图4　

解析：焦点F（3，0），点A、F在椭圆的异侧，PA+PF1≥AF1，当且仅当A、P、F1三点共线时取“等号”，故所求最小值是

变式：已知点A（1，1），F1是椭圆的左焦点，P是椭圆上任意一点，求|PF1|+|PA|的最小值与最大值.

解析：由椭圆定义|PF1|+|PF2|=2a=6，得|PF1|=6-|PF2|，所以|PF1|+|PA|=6-（|PF2|-|PA|）.

如图5，在△PAF2中，易知||PF2|-

|PA||≤|AF2|，即当点P位于点P1时，|PF2|-|PA|=|AF2|=，此时|PF1|+|PA|取得最小值，最小值为6-

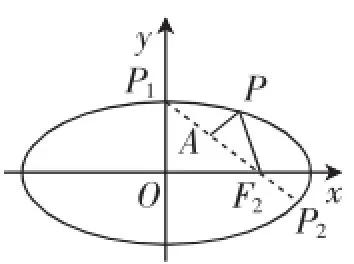
图5　

当点P位于点P2位置时，|PF2|-|PA|=-|AF2|=-此时|PF1|+|PA|取得最大值，最大值为6+

评注：通过利用椭圆定义将|PF1|+|PA|的最值问题转化为|PF2|-|PA|的最值问题，从而利用三角形两边之差小一动点，A（0，-5），B（5，0），求PA-PB的最大值.

3.在双曲线中的应用

例3已知P是双曲线因此AB：y=x-5和双曲线右支交于点P0，PA-PB≤AB=5，当且仅当P、A、B三点共线时取等号，即点P与P0重合，PA-PB的最大值为5

4.在抛物线中的应用

例4已知点P是抛物线y2=4x上的动点，F（1，0），A（4，3），则PA-PF的最大值和最小值是_________.

解析：如图6，可判断A、F都在抛物线的内侧，直线AF与抛物线相交于P1、P2两点，当PA≥PF时，根据“三角形两边之差小于第三边”，得PAPF≤FA，而FA=P1A-P1F可以取到，所以PA-PF的最大值是同样，当PA≤PF时，有PF-PA≤FA等价于PA-PF≥-FA，而FA=P2F-P2A可以取到，所以PA-PF≥-FA=-，因此PA-PF的最小值是-

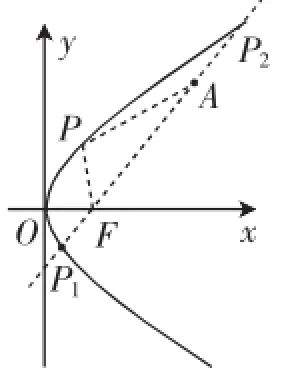
图6　

变式：若点A的坐标为（3，2），F是抛物线y2=2x的焦点，点M在抛物线上移动时，使|MF|+|MA|取得最小值的M的坐标为（）.

解析：利用抛物线定义|MF|+ |MA|=|MD|+|MA|，A、M、D三点共线时|MF|+|MA|取得取小值，此时点M位于M′时取得最小值，如图7，易知点M′的纵坐标与点A的纵坐标相同为2，将y=2代入抛物线方程y2=2x，得点M′的横坐标为2，故正确选项为D.

评注：本题通过利用抛物线的定义：到定点的距离与到定直线的距离相等，利用等量代换，将最值问题转化为模型问题求解.F C

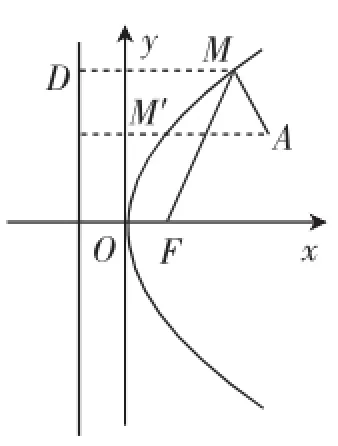
图7