从对一堂“建模课”的分析，谈教学设计的优化

☉江苏无锡市滨湖区教研中心　王华民

☉江苏无锡市宜兴市教研室　储六春

·江苏省无锡市王华民名师工作室·

从对一堂“建模课”的分析，谈教学设计的优化

☉江苏无锡市滨湖区教研中心王华民

☉江苏无锡市宜兴市教研室储六春

在无锡市学科带头人评选的赛课环节中，课题是《必修4》“1.3.4三角函数的应用”，是一堂数学建模课，笔者有幸作为评委，观摩了十多位选手精心设计的课，各显特色，但差异较大，差异主要体现在教学设计，根子在于对教材、学生和对教学的理解上.下文呈现教材内容，分析几个代表性的设计方案，谈谈教学设计的优化.

一、教材内容——1.3.4三角函数的应用

一句话：三角函数能够模拟许多周期现象，因此在解决问题中有着广泛的应用.

例1点O为做简谐运动的物体的平衡位置，取向右的方向为物体位移的正方向，若已知振幅为3cm，周期为3s，且物体向右运动到距平衡位置最远处开始计时.

（1）求物体对平衡位置的位移x（cm）和时间t（s）之间的函数关系；

（2）求该物体在t=5s时的位置.（解答从略）

例2一半径为3m的水轮如图1所示，水轮圆心O距离水面2m，已知水轮每分钟逆时针转动4圈，如果当水轮上点P从水中浮现时开始计算时间.

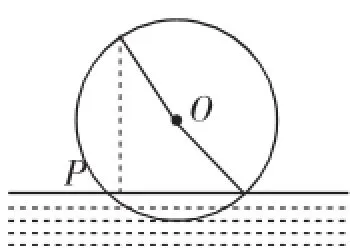
图1　

（1）将点P距离水面的高度z（m）表示为时间t（s）的函数；

探究案例港口水深的变化与三角函数（潮汐现象）（略）.

二、设计方案

教学参考建议本课题安排两节课，第一课时如何安排内容，设计流程？

［方案1］

（一）温故知新

问题1：如图2，某地一天从6时至14时的温度变化曲线近似满足函数T=Asin（ωt+φ）+ B，其中A＞0，ω＞0，0≤φ＜π.试写出这段曲线的函数解析式.

解答后说明：在现实世界中存在不少周而复始的现象，你能否再举几个例子？

（二）数学运用问题2：教材例1.问题3：教材例2.

（三）回顾小结（略）

设计意图：设计三个案例，分别为给图求解析式、简谐运动及水轮问题，分别对应三角周期函数在数学中的应用、在物理中的应用和在生活中的应用.三个问题由易到难，问题1是从学生熟悉的给图求解析式的情境入手，复习待定系数法求解，既有利于提高学生的自信心，也为问题2铺垫.问题2是突出数学和其他学科的整合.问题3是强化建模思想.

［方案2］

（一）情境导入

潮汐、弹簧、摩天轮等图片（分别对应后面的实际问题）.（二）数学应用

1.通过问题串复习回顾

问题1：单位圆中正弦线、余弦线，角α终边上一点P的坐标_________；

问题2：如图3，在半径为r的圆中，角α终边上一点P的坐标为_________；

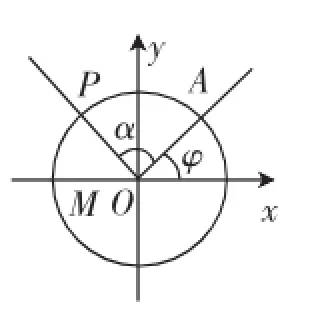
图4　

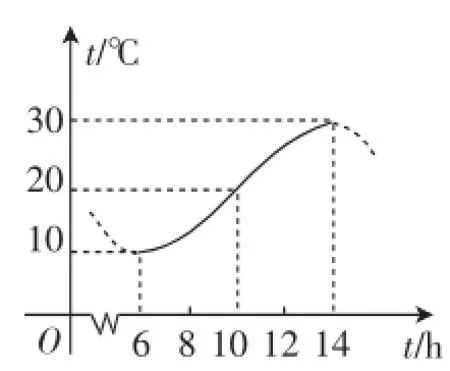
图2　

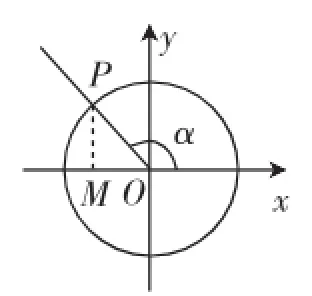
图3　

问题3：如图4，若以OA为始边，逆时针旋转α角到OP，则点P的坐标为_________；

问题4：如图5，若以OB为始边，逆时针旋转α角到OP，则点P的坐标为_________；

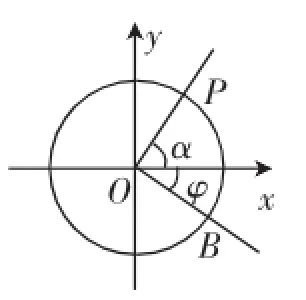
图5　

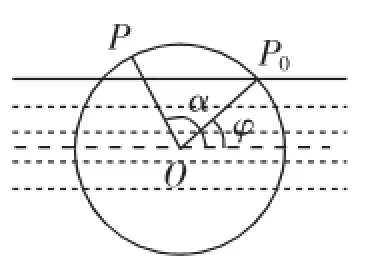
图6　

问题5：如图6，水轮每分钟逆时针转动4圈，t秒钟转过的角度是_________.

2.解决教材的例2（略）

变式：若水面由于降雨上升了2米，那么：

（1）点P距离水面的高度z（m）怎样表示为时间t（s）的函数？

（2）点P第一次到达最高点大约要多长时间？（略）

3.解决教材的例1（略）

（三）回顾小结（略）

设计意图：对于普通班的学生，理解数学是首要任务，没有理解，谈何教学.为突破例2这一难点，设置几个铺垫的问题，让学生拾阶而上.变式的目的是为了较好地检测学生掌握的程度.课堂反馈：学生较顺利地解决了例题及变式.

［方案3］

（一）情境引入

列举生活中的周期性；展示闹钟，引导学生观察：秒针一秒钟转过的角度.

（二）数学应用

1.教材例2

教师提问：如何刻画点P的位置？

学生略作思考，感到有困难，教师提出：我们从简单的问题开始探索，寻求方法.出示：

基本问题：如图7，一个半径为3m的水轮，水轮圆心O恰在水面上，已知水轮每分钟逆时针转动4圈，如果当水轮上点P从水中浮现时（图中P0）开始计时.

（1）将点P距离水面的高度z（m）表示为时间t（s）的函数；

（2）点P第一次到达最高点大约要多长时间？

变式1：点P在D（C、B）点时开始计时，函数的解析式又如何？

变式2：如图8，若水面由于干旱下降了2m，点P距离水面的高度z（m）怎样表示为时间t（s）的函数？

基本问题与变式题合起来，解决了例2.

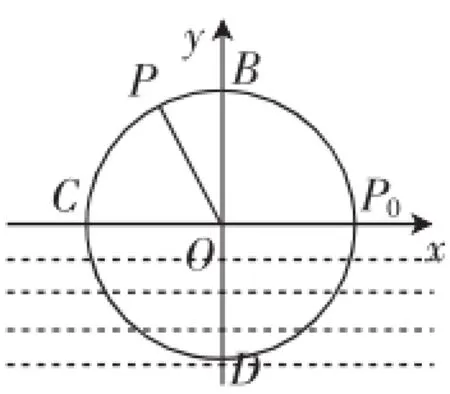
图7　

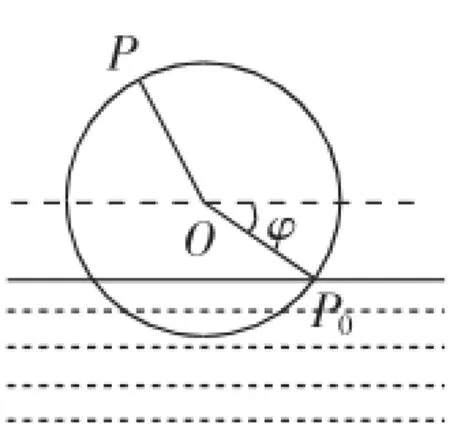
图8　

变式3：如图9，若水面由于降雨上升了2m，那么：

（1）点P距离水面的高度z（m）怎样表示为时间t（s）的函数？

（2）点P第一次到达最高点大约要多长时间？

（变式3作为学生练习）

过渡语：这道例题是周期函数在生活中的运用，改变观察角度，下面看周期函数在物理中的运用——简谐振动，出示例题.

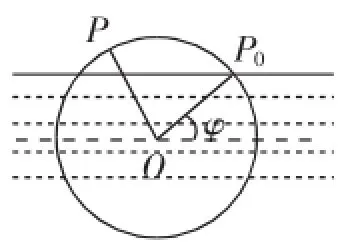
图9　

2.教材例1（略）

（三）回顾小结（略）

设计意图：从目标出发，先呈现未知问题，当学生感到有困难时，转向从特殊、简单的问题开始，积累一些解题经验，再来解决未知问题.让学生经历解决疑难问题由“未知→已知→未知”的探索过程.

［方案4］

（一）创设问题情境

情境：投影图片：明代科学家宋应星《天工开物》中的水车和三峡水电站的大型机组的图片，如图10.《天工开物》共三卷十八篇，全书收录了农业、手工业，诸如机械、砖瓦、陶瓷、纸、兵器、火药、纺织、采煤等生产技术，乃国学经典.

图10　

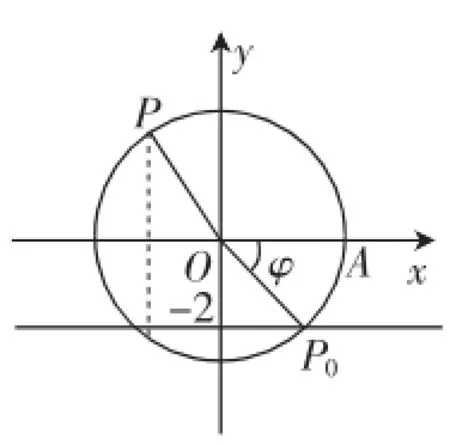
图11　

问题：从上述两幅图片看，水轮在生活中起了重要作用，水轮的运动特点是什么？用什么函数描述这种运动？

（二）数学应用

1.教材例2（把半径改为4m）

请学生读题、思考1分钟，教师通过设问、追问的对话，引导学生探究.

教师：同学们，我们先来明确一下，本题的目标是什么？

学生：如图11，目标z（m）表示为时间t（s）的函数.

教师：目标能否转化？学生：可以，z（m）=yP+2.教师：新的目标yP就是什么？（再明确）

学生：圆上动点P的纵坐标.

教师：求圆上动点P的问题有没有类似的解决办法？

学生：单位圆上学过，可表示为（cosα，sinα）.

教师：这里的α是多少？能否求出来？

教师：怎么求yP？

学生：利用三角函数定义，得yP=4sin

教师：是否需要建立直角坐标系？

学生恍然大悟.

教师：现在的起点不在A，怎么办？

2.用拟合法处理物理中简谐振动问题

（1）播放简谐振动动画，如图12.

图12　

（2）问题：点O是简谐运动物体的平衡位置，取向右方向为物体位移的正方向，下表是物体对平衡位置位移x（cm）和时间t（s）的关系表：

t（s）00.511.522.53 x（cm）1.531.5-1.5-3-1.51.5

试求出物体对平衡位置的位移x（cm）和时间t（s）之间的函数关系.

教师引导学生观察表格中数据，让学生联想，可以通过描点、画散点图、拟合，选择正弦型函数x=Asin（ωt+ φ），再用待定系数法求解.

3.教材的例1，作为学生的练习

（三）回顾小结（略）

设计意图：从生活中的问题出发，古代文明与现代工程都涉及水轮，如何用合适的数学模型刻画水轮上点P在水轮上的运动位置？自然引起学生的兴趣与关注；通过播放动画再呈现问题，旨在让学生感悟数学来源于生活.之后对例2的探索突出了目标意识在解题中的运用.例1虽容易理解，但教材直接给出了简谐振动的函数关系，学生心存疑惑，则设置一道简单探索题复习拟合法建模，把例1作为练习.

［方案5］

（一）问题引入

教师演示弹簧实验，学生观察物理现象中蕴含的数学问题，引入新课.

（二）数学应用

1.教材例1

2.教材例2（半径改为4m）

解答后出示一道思考题：试问是否存在一个2.5s的时间段，点P在这个时间段的高度变化超过32m？为什么？

3.（教材中探究性案例，数据有改编）对结论用“几何画板”演示

（三）目标检测：弹簧振子的巩固练习（略）

（四）回顾小结（略）

设计意图：由于教材中的探究性案例是一个反映潮汐现象，体现三角周期性变换和数形结合的经典问题，一般用拟合法建模.由于运用了多媒体辅助教学，可以提高课堂容量、加大思维训练量，把“教参”建议的两课时并入一课时，把该案例放入其中，同时增加一道巩固练习.

三、在“三个理解”精神下谈教学设计的优化

1.对教材、学情及教学的分析

章建跃先生提出的三个理解，即理解数学、理解学生和理解教学，是数学教师专业发展的三大基石，也是优化教学设计的重要依据.

（1）理解数学是课堂教学“预设”的前提，也是课堂教学“生成”的关键，教师只有清晰地知道所教内容“是什么”，深知数学知识所蕴含的思想方法和价值，才有可能制定合理的教学目标，并准确实施.本课题是苏教版高中数学必修4的第一章最后一节，其目的是让学生感受三角函数在解决具有周期性变化规律的实际问题中的应用，体验三角函数与日常生活和生产实际的联系；掌握建立函数模型解决实际问题的基本思路，增强学生应用数学的意识.教材共设置了两个例题，一个探究性案例.例1是三角函数在简谐运动中的运用，教材中的解答：设x和t之间的函数关系为x=3sin（ωt+φ），然后用待定系数法求解.例1反映了只要是“周而复始”的运动，都可考虑用x=Asin（ωt+φ）+B的模型去解决.但简谐振动为何是这个关系？学生心存疑惑，故有必要暴露知识的形成过程.例2的水车问题是三角函数在圆周运动中的运用，综合性强，它既要求能把水轮每分钟逆时针转动4圈转化为角，知道半径为r的圆上一点的坐标表示，还要对角的始边OP0与x轴的正半轴差一个角φ进行转化，是教学的难点.本课的关键是如何突破这个教学难点.教学重点是领悟在实际问题中建立三角函数模型的基本方法.

（2）理解学生就是要解决“教给谁”的问题，因为学生是课堂教学的主体，教师只有弄清学生已有的数学知识、方法、经验、兴趣和思维特点等，才能做到有的放矢，既激发学生积极情态，又提质增效.学生是四星级高中的高一学生，他们基础好，思维敏捷.在必修1函数教学中，学生已经学习过拟合法建模，但有所遗忘.

（3）理解数学教学就是要解决“怎样教”的问题，要遵循数学教学的规律，采用科学、合理的教学方式.新课标倡导自主探索、动手实践、合作交流等学习方式，注重提高学生的数学思维能力，但需统筹兼顾，其一，训练思维必须要符合学生的特点，在认知的最近发展区内进行；其二，课堂是限时的，每节课都有一定的教学任务，需要关注教学的有效性.因此，必须把握好思维训练和铺垫的度.其实数学解题的过程也是一个思维不断深入的过程，随着知识面不断拓宽，学生的数学思维也在不断经历着由浅入深、由单维到多维的变化，所以提高学生的解题能力（如本课对难点例题的突破），也是培养学生思维能力的一个很好的着力点.又如，外因要通过内因起作用，提倡“做中学”，学之道在于“悟”，需要留给学生一定的思考和感悟的时间等.对于这堂习题课，重点是要控制好题量，合理安排探究活动.

2.对五个教学方案的对比分析

上述五个方案都能精心创设好的问题情境，既提升学生的学习兴趣，也与本课例题有关联.其中方案4最精彩，创设两幅图片的情境，《天工开物》乃国学经典，三峡水电站堪称世界之最，无论是古代文明还是现代宏伟工程都涉及水轮，提出的问题有助于学生解决例2这一难点，这是理解学生的体现.五个方案在解题时都有一个“审题”环节，教学生从习题中提取有效信息，在解题后都有小结反思，这是理解教学的体现.

五个方案的差异主要体现在以下两方面.其一，选择习题及题目的数量上，五个方案都选择了教材的例1、例2，方案一增加了一道数学解析式作为铺垫；方案二、三增加了对例1、例2的变式；方案四在例1前增加了一道简单探索题；方案五增加了一道探究性案例和一道巩固性练习.另外，方案二、三、四调整了教材中例题的顺序，意在把水轮问题作为研究的重点，方案三还用“改变观察角度”作为过渡语，更显自然.选题的多少、呈现顺序的不同，说明教师在三个理解上存在一定的差异.

其二，对于难点的处理上，五个方案的思维量有较大的差异，说明教师自身对培养学生思维的认识和水平上存在一定的差异.方案一呈现的三道问题，分别对应三角函数周期性在数学、物理和生活三个方面的应用，比较全面，但因多了一道求解析式问题，对解决例2这一难点显得匆忙，不利于学生有效突破；问题1复习待定系数法是为例1铺垫，其实待定系数法早在初中就学过、用过，这些学生解决例1没有任何障碍，不需要铺垫.可见，教者在理解数学、理解学生上欠考虑.方案二中因设置铺垫问题较多，有益于学生理解内容，但留给学生思考的空间较小，思维训练量不足，长此以往学生会产生思维上的惰性，在面临新问题时将束手无策，该方案适用于层次较低的班级.方案三比方案二多了一个过程：先呈现未知问题，有困难，从特殊或简单的问题开始，积累了一定的解题经验，再来解决未知问题.其中从特殊到一般的方法，是解决新颖、疑难问题的基本思路和方法，这种让学生经历探索过程，教学生学会思考的做法，很值得称道.该方案进行了几个变式训练，变式3作为学生的巩固练习，有益于提升有效性.这个方案适宜于中等层次班级的学生.方案四通过设问、追问获得解答，是目标意识在解题中的运用.当我们面对一个未知问题时，意识首先做出反映，“目标是什么”，“如何达到目标”，目标意识促使我们开始就接触到问题的核心.本题在明确目标后，进行目标转化或分解，面对新的目标，又在回忆过去是否遇见类似或相近的问题，发现了单位圆中的坐标表示，可以用三角函数定义解决.当目标的起点在P0时，则寻求两者的关系，进行转化.这样总是围绕目标在思考、探索，促使已有知识或经验再现，进行联想、类比与转化，从而达到目标.另外，教师设置一道简单探索题，把例1作为练习，给学生观察发现的机会.可见，学生得到较多的思维训练，该方案对学生的思维要求较高，适宜于层次中等或较高的班级学生.方案五的习题量和思维训练量都很大，一批优秀学生受益匪浅.教师有较强的课堂掌控水平，呈现的问题在课堂上都解决了，但大多是教师带着学生完成的，学生独立思考、操作的时间显得不足，有违“做中学”、“悟中学”的学习规律，一些中等及中等以下的学生难免吃“夹生饭”，影响教学的有效性.

3.对教学设计进行优化

根据“三个理解”精神，笔者觉得需要对上述教学设计进行优化.实践表明：教学需要一点铺垫，铺垫有益于学生理解，但不利于培养学生思维.因此，要求教师基于学情，把握好铺垫的度.上述五种方案，方案一探索过程未能充分展开，对学生思维能力的培养略显不足，建议删除问题1，增加对问题2的描点、探索的过程，对问题3要多留一点探索的时间和空间.方案二有益于学生理解数学，但不利于学生思维能力的培养，可借鉴方案三、四做一些微调；方案五教学容量和思维容量都偏大，建议删除例3和目标检测题，例1可以像方案四那样设置一个拟合法建模的过程，例2中增加探索、思考的时间.方案三可以借鉴方案四中例1的处理.方案四最为精彩，经常进行目标意识的训练，对培养学生的思维、提升课堂的有效性都很有意义.

解学生之疑难是教师的一个重要职责，对于本课，突破建模之难点，就可以使学生轻装前行，增强学习数学的信心.优化设计需要权衡多个元素，把握好度，但重点是进行有效的思维训练，促进学生理解数学；优化设计也是一个不断完善的过程，虽然教师和学生都在变化，但变化中存在不变性（规律），就是“三个理解”.F