小先生制在中学数学概念教学中的尝试

☉江苏省如皋市搬经中学　丁祥

小先生制在中学数学概念教学中的尝试

☉江苏省如皋市搬经中学丁祥

一、界定

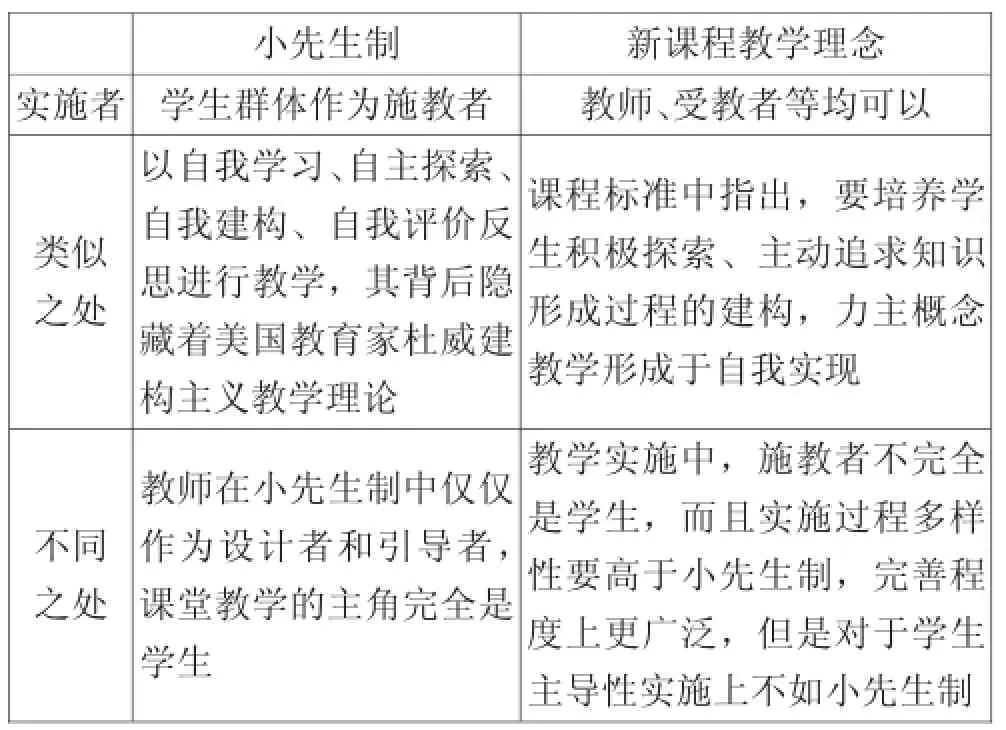
小先生制新课程教学理念实施者学生群体作为施教者教师、受教者等均可以类似之处以自我学习、自主探索、自我建构、自我评价反思进行教学，其背后隐藏着美国教育家杜威建构主义教学理论课程标准中指出，要培养学生积极探索、主动追求知识形成过程的建构，力主概念教学形成于自我实现不同之处教师在小先生制中仅仅作为设计者和引导者，课堂教学的主角完全是学生教学实施中，施教者不完全是学生，而且实施过程多样性要高于小先生制，完善程度上更广泛，但是对于学生主导性实施上不如小先生制

我国教育家陶行知先生在其教育理论中率先提出了“小先生制”.顾名思义，小先生制的意思是教师通过合理的教学设计（教师是教学的设计者和引导者），将教学内容通过教学群体中的出类拔萃者来实施，并在实施过程中依赖这些小先生去自我判断、调整、实施，教师的职责继续将在课堂中给予小先生教学进行修正.在陶行知先生所处教学年代里，小先生制一直占据教学主导地位的一种教学制度.笔者认为，小先生制与新课程教学理念有着如出一辙的本源，通过下表我们可以看出小先生制与新课程教学理念之间的相似之处与不同之处：

从陶行知先生的小先生制，我们可以看到教学中实施需要教师引导学生如何成为小先生？成为小先生后如何将学生思考问题的角度按照学生的视角出发、问题分析等.笔者认为课堂教学的小先生制实践，有这些方面的保障：其一，对于学生可以实施与否需要教师对课程的合理教学设计；其二，实施小先生制对于学生思考而言比较有利，因为小先生的思考角度往往是从学生思维出发的，这样的教学比较符合学生认知心理；最后，教师必须时刻提醒自己是教学实施的引领者、设计者，而非实施者，切勿主次颠倒.

二、小先生制实施

笔者采用课程《点到直线的距离》一课进行了充分设计，以小先生制实施本课的初步探索.笔者制定合适的教学设计和选择表达能力相对较强的小先生，分析学生作为小先生后对该数学概念教学实施的可能性、正确性、合理性等.

（一）方法设计

小先生制的引入，笔者将启用小先生替代教师，用他们的学生似眼光去分析问题、解决问题，引导其他学生进行公式的推导、探究等，通过新颖的探究式教学方式，积极调动学生参与概念教学的积极性，提高数学教学的有效性.

（二）教学实施

1.教师给出问题情境

如图1，公路附近有一家超市，为了使超市到高速公路的运输费用最低，要求铺一条连接超市和公路的道路.同学们设计一下怎样铺路可以使运输的费用最低？

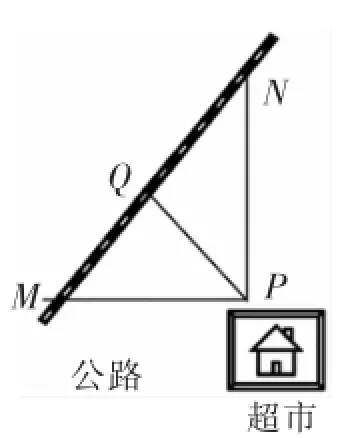
图1　

学生探究：学生通过探究发现点到直线的垂线段距离最短即PQ.

学生思考：若PM=3公里，PN=4公里，∠MPQ=90°，可知超市到公路的最短距离PQ为多少？

学生探究：学生根据面积相等可直接求出PQ的距离.

设计意图：创设问题情境，激发学生的学习欲望.由生活的数学问题引入本课，激发学生学习数学的兴趣.同时感受到数学源于生活，并应用于生活，数学与生活息息相关.

2.小先生引导新知探究

小先生A（教师选择的是语言表达能力比较强的学生作为教学流程进行的小先生）：我来将问题抽象为数学背景下的问题，我们来看看问题的本质.

问题：已知点P和一条直线l，怎样求点P到直线l的距离d，P（x0，y0），l：Ax+By+C=0（AB≠0）.按照教师事先设计的分组，小先生将学生分组讨论，合作交流：

学生进行方法探究后，小先生请学生尝试探索解题的步骤：（1）从情境问题给出的图形，估计通过讨论可能寻求到下面的解法：求出过P点与x轴平行的直线PM，求出与l的交点M的坐标，再求出|PM|，求出过P点与y轴平行的直线PN，求出与l的交点N的坐标，再求出|PN|.上述方法的算法流程图是什么？（2）学生求出直线PQ的方程，再求两直线的交点Q，再根据前面所学的两点间的距离公式进行求解.

3.小先生引导下的共同探究点到直线的距离公式

小先生A：大家看看图中的直角三角形，我们如何利用新的思路解决？

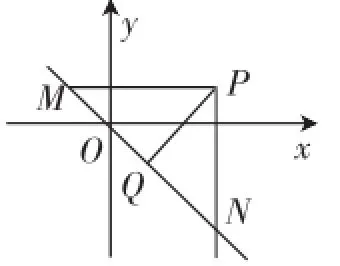
图2　

学生：求距离，我们往往可以使用初中直角三角形中的等面积法.

小先生A：请同学们分组尝试，动手试试.（教师此时不断走动巡视，看看学生解决问题的实际情况如何）

学生：刚刚我用一组特殊的点，求了一下比较简单，好像用字母的运算非常烦琐.

小先生A：的确是.我第一遍演算也非常困难.看看有没有其他同学算出来？（大概十来分钟，教师发现学生无法迅速解决本题的字母运算，此时课堂比较沉默，教师看到此情形应该出来进行课堂的过渡）

师：流程同学们都很清楚，为什么大家无法一遍算清楚呢？这里涉及到大量的字母运算.我们知道，抽象的字母运算，同学们都比较生疏，我们请小先生B给大家板演下.

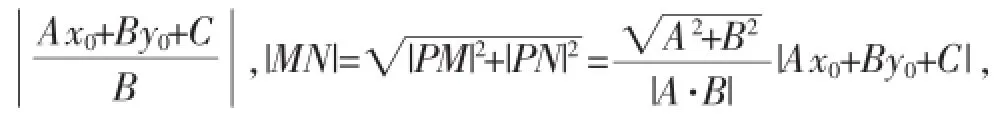
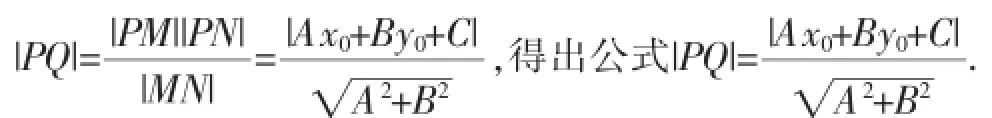
（注：这里直线方程设为一般式，A、B为直线一般式方程中的系数）

设计意图：多种方法进行探究，培养学生自主探究和发散思维的能力，同时培养学生合作学习的意识.学生体会算法思想，学生体会合作学习的乐趣.学生体会探究成功的喜悦.因为公式推导较难，学生初始解答并不成功，教师适时加入小先生的引导，通过学生对到加深其他学生对公式的记忆.

小先生A：刚刚大家对问题的探究属于直线斜率存在且不为0的情形下分析的，这个公式对于斜率为0或者斜率不存在时还能适用吗？请大家试试.

学生：适用.刚刚用特殊情形检验，我发现成立.

设计意图：通过公式特殊情形的合理推导，教师适时加入将数学公式的开放性说明得毕露无遗，也无形中提高了学生对于数学公式一般性和特殊性的整合认知.

4.巩固训练

小先生A：请看下列问题，请四位同学板演：

训练：（1）点P（1，0）到直线l：2x-3y+1=0的距离；（2）点P（-1，1）到直线l：y=3x-2的距离；（3）点P（2，-1）到直线l：x=5的距离；（4）点P（-3，-2）到直线l：的距离.

设计意图：（投影学生解答并与学生共同小结）①直线的方程要化成一般式；②分子是用点的坐标代入直线方程左边再取绝对值；分母是直线方程中x，y系数平方和的算术平方根.小先生A充分实施教师的职责，将公式初步运用问题合理地请学生尝试公式运用，并从中感受直线方程的使用形式.

5.合作再探

教师设计：等腰三角形底边延长线上一点到两腰所在直线的距离之差与一腰上的高有何关系？

小先生A：（用几何画板演示）大家看到了什么？可以得到什么结论？

学生：等腰三角形底边延长线上一点到两腰所在直线的距离之差等于一腰上的高.

小先生A：证明过程请大家想想.

设计意图：教师估计学生可以寻求到几何法与解析法，但是具体实施需要时间操作，此处比较适宜机动操作，证明过程省略.

三、课例反思

本课是笔者首次借助教育家陶行知先生的小先生制实施的一次教学探索课程.笔者在教学过程中体会了以往所有教学课堂不一样的氛围和感受，看到两位小先生在教学实施过程中的成功之处与不足之处.最令笔者意外的是，小先生对于教学的一些言语和分析比较符合学生认知的心理，小先生和学生一起对公式的推导过程让学生听课的效率有了不小的改变.初次探索之后，笔者也有了一些思考：

（1）小先生制的成功与否与课程选择的内容密切相关.本节课笔者由于经验不足选择了内容较为复杂的公式推导，尽管小先生非常清楚地展示了推导过程，但是能完全通过小先生分析进而推导出公式的学生几乎没有，存在的不足是笔者教学设计中预料不到的，小先生的临场应变能力也稍显不足.笔者建议以后对小先生制的尝试可以选用章节的起始课等更为简单的课程比较适宜.

（2）小先生制强调的主要是学生引领下的一种教学探索模式或制度.笔者认为这种制度在积极性和创新性上有着长足的进步，而且真正让教师成为了一种设计者和引导者，相比新课程美其名曰的伪探索前进了一大步.但是这样的教学需要更为细致的设计和人员的挑选，这些都是多次实践才能形成体系，需要不断地积累经验.

（3）在新课程强调积极建构、主动探索的今天，小先生制不仅适合了新课程教学理念，其更突发奇想的将课堂概念教学完整的呈现在学生面前，于学生而言正是一种教学新方式的尝试，于教师而言是一种新的摸索，笔者期待后续教学研究更为完善.

1.周丽娇.浅谈“小先生制”在数学教学中的应用［J］.教育教学论坛，2011（25）.

2.朱月珍.关于数学教学中创造性思维的引导［J］.数学教学研究，2009（2）.

3.陈树康，杨学枝.浅谈新课程下数学教学中的三个问题［J］.中学数学教学，2009（5）.Y