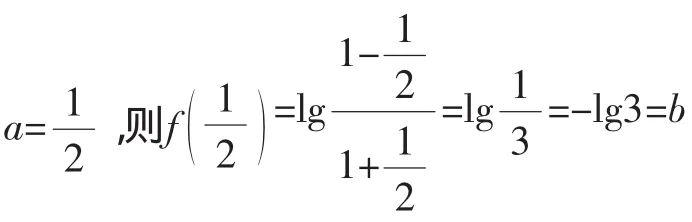例说数学思想在高中数学解题中的运用
2016-11-19江苏省泰兴市第四高级中学肖雪平
☉江苏省泰兴市第四高级中学 肖雪平
例说数学思想在高中数学解题中的运用
☉江苏省泰兴市第四高级中学肖雪平
函数是高中数学中的重要内容,高中数学大部分章节都涉及函数或函数思想方法,是高中数学的一条主线.纵观中学数学,可谓是以函数为中心,以函数为纲,“纲举目张”,抓住了函数这个“纲”就带动起了中学数学的“目”.即使对函数极限、导数的研究,也完全是以函数为对象、为中心的.熟练掌握基本初等函数的图像和性质,是应用函数与方程思想解题的基础.善于根据题意构造、抽象出函数关系式是用函数思想解题的关键.在教学中,若能根据题设特点,灵活地运用相应的数学思想,往往能化难为易,化繁为简,从而优化解题过程,达到培养思维的目的.
一、方程思想
方程思想,就是分析数学问题中的变量间的等量关系,从而建立方程或方程组,通过解方程或方程组;或者运用方程的性质分析、转化,使问题获得解决.
例1已知数列{an}满足an+2=an+1-an,a1=1,a2=2,求
解:记f(n)=an,则有f(n+2)=f(n+1)-f(n),对于函数f(x),若有f(x+2)=f(x+1)-f(x),则有f(x+3)=f(x+2)-f(x+ 1),将上面两式相加,则有f(x+3)=-f(x),(*)即有f(x+6)= -f(x+3)=-(-f(x))=f(x),因此可知函数f(x)的周期为6,可知数列{an}的周期也为6,而且借助(*)可求得f(x)+ f(x+1)+f(x+2)+f(x+3)+f(x+4)+f(x+5)=0,所以对于数列{an},也有a1+a2+a3+a4+a5+a6=0,所以S2013=a1+a2+a3=a1+a2+(a2-a1)=2a2=4.
点评:本题是通过对数列的各项之间的规律的探究,构造函数来发现周期性,并将周期性运用到数列前n项和的求解中,使得求解直观而且简便,这体现了函数思想的在数列求解问题中的作用,根据题设条件灵活地构建方程是解决本题的关键.
二、化归与转化思想
化归与转化思想是数学中最基本的思想方法,是指在解决问题时,采用某种手段使之转化,进而使问题得到解决的一种解题策略,是数学学科的一个特有的思想方法.化归与转化思想的核心是把生题转化为熟题,将复杂问题化归为简单问题,达到最终解决问题的目的.
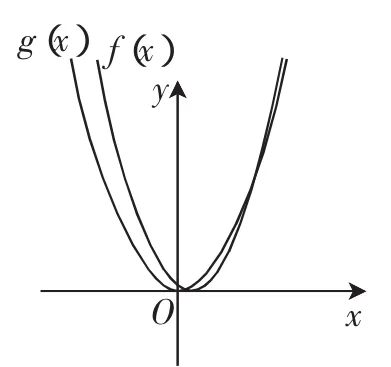
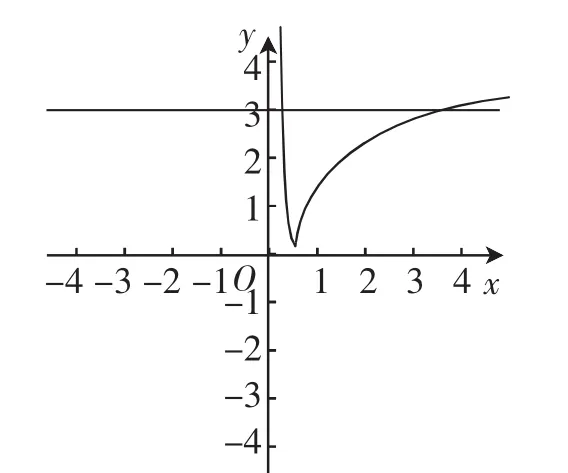
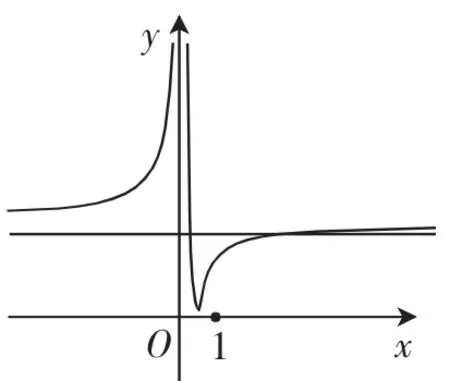
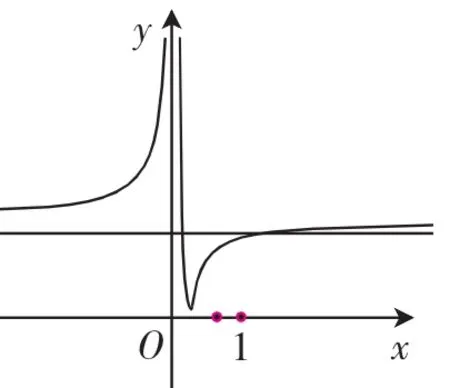
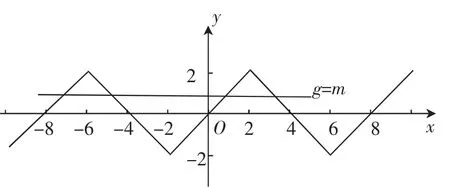
例2若关于x的不等式(2x-1)2 分析:对不等式(2x-1)2 (一)代数法(解一次、二次不等式,研究解的个数) 方法1:由题意可知,a>0, 若a≥4,x有无数解,舍去; 当x=0时,x无解,舍去. 方法2:将不等式(2x-1)2 要使恰有3个整数解, (二)几何法(数形结合,用基本函数图像研究解的个数) 方法3:设f(x)=(2x-1)2,g(x)=ax2. 当a=0时,y=g(x)表示x轴,舍去. 当a<0时,y=g(x)表示开口向下,对称轴为y轴的二次函数图像,舍去. 当a>0时,y=g(x)表示开口向上,对称轴为y轴的二次函数图像,由ax2>(2x-1)2,得g(x)>f(x),即恰有3个整数x值,使得g(x)的图像在f(x)图像的上方, 图1 方法4:研究不等式ax2>(2x-1)2. 当x=0时,不满足,舍去. 图2 则g(3) 方法5:研究不等式ax2>(2x-1)2. 当x=0时,不满足,舍去. 图3 方法6:研究不等式ax2>(2x-1)2. 由题意可知,a>0. 当x=0时,不满足舍去. 图4 如图4, 点评:对于代数法可以通过化归,避免讨论;对于几何法更要通过化归转化为基本函数,并利用函数图像解决问题.在方法3、4、5、6中,化归程度层层递进,化归得越彻底,得到的基本函数图像越容易,解答也就越简单.函数不断等价转化的过程,正是数学思维力的体现. 化归与转化和数形结合是高中的重要思想方法,我们将陌生的函数转化为熟悉的函数,将复杂的函数转化为简单的函数,然后通过研究基本函数图像,找到解题的路径.层层转化,化繁为简需要学生有扎实的基本功,敏锐的观察力和解题时的一丝灵感. 根据数学本质属性相同点和不同点,确定划分标准进行分类,然后对每一类进行求解,科学合理的分类以互质、无漏、最简为原则. (1)求f(x)在[0,+∞)内的最小值; (2)设曲线y=f(x)在点(2,f(2))处的切线方程为y=,求a,b的值. 解:(1)设t=ex(t≥1), 点评:本题是考查函数、导数的基础知识,需要分类讨论、化整为零,各个击破从而求出答案. 数形结合思想是将抽象的数学语言与直观的图形结合起来,与抽象思维结合起来,实现抽象概念与具体形象联系和转化. 例4f(x)为R上的奇函数且x∈[0,2]时,f(x)单调递增,对x∈R有f(x+4)=-f(x),g(x)=m(m>0),设f(x)= g(x)在[-8,8]上有四个根x1,x2,x3,x4,则x1+x2+x3+x4= ______. 解:作出f(x)在[-2,2]上的图像,再由f(x+4)=-f(x)知,T=8.由f(x+2)=f(2-x)知,对称轴x=2,作出f(x)在[2,6]上图像,则得到f(x)在[-2,6](在一个周期)内的图 像,左、右平移得[-8,8]上的图像如图5所示. 图5 整个问题置于图像中即为整体观的运用,虽然x1,x2,x3,x4随直线g(x)=m的移动存在变化性,但x1+x2=2×(-6),x3+x4=2×2则始终不变,故x1+x2+x3+x4=-8. 点评:本题若利用代数法是不可能求出α与β的值,从而不能求出α+β的值,而运用数形结合思想可以间接巧妙地求出α+β的值. 特殊性寓于普遍性之中,具体问题、具体分析,通过特例分析,往往能获得解题的重要信息,达到减缩思维过程,降低推算难度的目的. 点评:考虑本题是选择题,a、b是用字母表示的数,我们不妨用特殊值来研究,答案来得简单. 总之,数学思想是从数学内容提炼出来的数学知识精髓.只有运用数学思想方法,考查函数概念、性质及导数等基础知识,考查函数极值、函数单调性、零点,考查数形结合、分类讨论等思想方法,才能使数学知识转化为分析问题,解决问题的能力,才能体现数学学科特点,才能形成优秀数学素养.
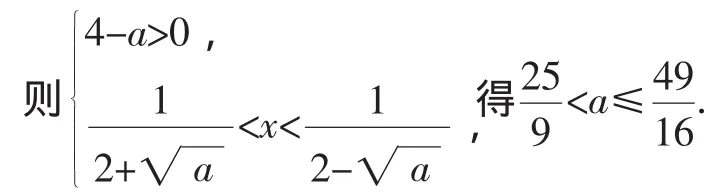
三、分类与整合思想

四、数形结合思想
五、特殊与一般的思想