基于多项式一致逼近的多阈值图像分割算法

2016-11-24卫颜俊冯博琴伍卫国

通信学报 2016年10期

关键词：伯恩斯坦极值直方图

卫颜俊，冯博琴，伍卫国

（1. 西安交通大学计算机教学实验中心，陕西西安 710049；2. 西安交通大学计算机系，陕西西安 710049）

基于多项式一致逼近的多阈值图像分割算法

卫颜俊1，冯博琴1，伍卫国2

（1. 西安交通大学计算机教学实验中心，陕西西安 710049；2. 西安交通大学计算机系，陕西西安 710049）

针对传统多阈值图像分割算法的计算复杂性，以及由图像直方图中毛刺的干扰带来的算法不稳定等缺点，提出一种基于伯恩斯坦多项式一致逼近的多阈值图像分割算法。首先根据逼近论中的威尔斯托拉斯定理构造图像直方图曲线的伯恩斯坦多项式，然后将图像直方图的峰谷值计算问题化简为伯恩斯坦多项式的极值问题，该极值问题可由伯恩斯坦多项式函数的一次、二次微分导出，最后依据这些极值和极性应用分类算法自动标注图像直方图的实际峰谷值，由此完成基于多阈值的图像分割。实验结果表明所提算法不受直方图中毛刺的干扰，算法整体稳定，冗余计算少，时间复杂度小，用时少，效率高，逼近性能和分割效果更好。

图像分割；图像直方图；阈值；一致逼近；伯恩斯坦多项式；距离空间

1 引言

因特网上每时每刻都在发生着巨量的数据交换，内容除了文本信息之外，很大一部分都是数字图像和视频信息，对数字图像处理方法的研究就显得非常重要。图像分割又是整个图像处理的一个重要的阶段，它直接影响到图像的特征提取、目标识别和计算机视觉等后期处理。图像分割一般是指根据图像中的灰度、颜色、纹理、形状和边缘等特征把图像划分成若干互不重叠的目标和背景的2个区域，并使这些特征在同一区域内呈现出相似性，而在不同区域间呈现出明显的差异性。图像分割方法总体可分为基于阈值、基于边缘检测、基于区域提取和结合特定理论的方法等。而基于阈值的分割方法又可以分为全局阈值法、自适应阈值法、最佳阈值法和数学理论阈值法等。其中，全局阈值法包括图像直方图的峰谷法、迭代法、最大类间方差法和最大熵自动阈值法等[1～6]。

但是在图像有噪声的情况下，其直方图包含有毛刺，此时的问题变得复杂化，以上这些求阈值的方法就不再能很好地适合，通常的做法是使用一维滤波等手段对直方图先进行平滑处理，然后再进行分割。

进一步，SHEN等[7]提出了一种新的自适应图像分割方法，它是一种基于灰度图像直方图熵和遗传算法相结合的算法，将分割问题重新定义为一个优化问题来解决。王亮申等[8]提出了适应度标定公式，使适应度函数能够正确引导群体的发展方向，从而提高收敛速度，分割方法仍然采用最大类间方差法来进行。李哲学等[9]提出的快速多阈值图像分割法其实是对最大类间方差法的二分法扩展。安丰玲等[10]利用多阈值分割结果，通过全局内区间直方图的均衡和基于均衡直方图对区间内的灰度拉伸，实现了图像增强，尽管是图像增强方法，但在图像分割中也值得参考。邢延超等[11]提出了一种基于知识的多阈值融合的图像分割新方法，将图像各位置的最佳连通域组合为最终图像分割结果，特点是将融合的先验和智能方法引入图像分割。曹增强等[12]提出了一种去除图像毛刺的快速算法，该方法克服传统的中值滤波的缺点，通过对毛刺形状归类，跟踪毛刺穿插于边界的整个过程，快速消除图像毛刺。黄琴波等[13]概述了如何将模糊方法、活动轮廓模型、遗传算法和神经网络等最新理论和思路应用在图像分割领域中。许新征等[14]也进一步概述了图像分割的新理论和新方法，比如数学形态学、模糊集、神经网络、支持向量机、免疫算法、图论和粒度计算等在图像分割方面的应用。

还可以采用数学理论求阈值，使用数学统计方法、聚类分类方法、泛函分析方法[15]、代数插值方法、样条函数方法以及函数逼近理论方法[16]。

程东旭等[17]对基于样条插值的图像分割算法进行了研究，使用样条插值方法对图像的灰度直方图进行曲线拟合，获得直方图的曲线表达，再利用对函数求极值的方法获取阈值，进而对图像进行阈值分割。陈争光等[18]也进行了类似的研究工作。

本文提出一种借助于逼近论中的伯恩斯坦多项式函数一致逼近方法来进行基于多阈值的图像分割。该方法以逼近理论为前提，比传统的阈值方法求解步骤简单，比一般的数学插值方法的计算过程简单，可操作性和应用性也较强，支持图像分割中直方图的去噪和多阈值求解。

数字图像在数字化和传输过程中时常带有噪声干扰，其灰度直方图自然也会出现噪声，主要表现是直方图曲线上的大量毛刺现象。借助于伯恩斯坦多项式的光滑性、保凸性、保符号性和保单调性等诸多优良性质，其对一般曲线的全局轮廓逼近非常好，从而避开了直方图曲线上的噪声，并通过多极值的求解很快获得原直方图曲线上的多峰谷值，从而获得多阈值。

2 灰度直方图的伯恩斯坦一致逼近多项式

2.1 威尔斯托拉斯定理

1885年，威尔斯托拉斯（Weierstrass）提出了对于连续函数，记作 f(x)，存在多项式逼近函数，记作P(x)，以下是威尔斯托拉斯第一逼近定理[19]。

设 f(x)是[a,b]上的连续函数，则∀ε＞0，∃P(x)多项式满足不等式

对于∀x∈[a,b]一致成立。

2.2 伯恩斯坦定理及伯恩斯坦多项式

1912年，伯恩斯坦（Bernstein）针对上述威尔斯托拉斯定理中的P(x)，构造出以下的一种特殊一元n次多项式函数，称为伯恩斯坦多项式，记作Bn(f,x)。

通过伯恩斯坦多项式，伯恩斯坦构造性地证明了威尔斯托拉斯定理，以下是伯恩斯坦逼近定理[19]。设f(x)是[0,1]上的连续函数，则伯恩斯坦多项式Bn(f,x)在[0,1]上一致收敛于 f(x)。伯恩斯坦定理不但证明了而且在 f(x)于[0,1]的各阶导数存在的前提下，还进一步证明了Bn(f,x)的各阶导数也一致收敛于 f(x)相应的各阶导数。本文用到Bn(f,x)及其一阶、二阶导数。

2.3 伯恩斯坦多项式的性质

伯恩斯坦多项式具有以下几个重要性质。

1) 保单调性质

如果f(x)是[0,1]上的单调增（减）函数，则Bn(f,x)也是[0,1]上的单调增（减）函数。

2) 保符号性质

如果f(x)≥0对x∈[0,1]成立，则Bn(f, x)≥0对x∈[0,1]也成立。

3) 线性性质

对定义在[0,1]上的2个函数f(x)和g(x)，以及任何实数 α 和 β，则 Bn(αf+βg,x)=αBn(f,x)+ βBn(g,x)成立。

4) 保凸性质

设 f(x)是[0,1]上的凸函数，则 Bn(f,x)也是[0,1]上的凸函数。

5) 磨光性质

不论 f(x)曲线在[0,1]上的规整性如何，Bn(f,x)经过反复作用总会将曲线变为由其2个端点构成的线段，即f(0)+[f(1)−f(0)]x。

6) 不动点性质

对线性函数 f(x)，Bn(f,x)具有不动点特性，即Bn(f,x)=f(x)。

总之，任何曲线与y=Bn(f,x)的交点数目都不大于曲线y=f(x)与y=Bn(f,x)的交点数目，Bn(f,x)几何形态上非常相似于f(x)，但其光顺性却不低于f(x)。

以上这些性质对本文非常重要，下面就利用它们进行直方图曲线的逼近。

2.4 伯恩斯坦多项式的推导

本文的问题针对的是 x∈[a,b]的情况，可使用变换公式，将x∈[a,b]的问题变为t∈[0,1]的问题，从而得出满足[a,b]区间与式(2)对应的伯恩斯坦多项式。其中，f(x)为图像灰度直方图离散曲线函数。

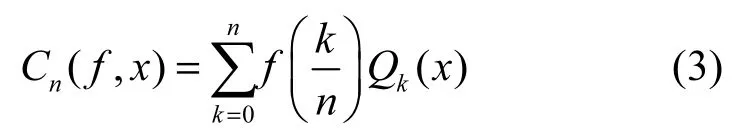
为了算法与编程的需要，将 Qk(x)代入式(3)，并做进一步的推导简化后得到式(4)。式(4)的通项中含有4个子项，已用中括弧标记出来，如果将第4子项，即设计为向量并先行计算，则整个式(4)对每个x（x∈[a,b]）来说的时间复杂度为O(n)。

根据图像灰度直方图的特点，可取[a,b]= [0,255]。

图1为Lena样本图像，图2和图3分别是图1所对应的灰度直方图和n次逼近的伯恩斯坦多项式曲线（取n=1200）。从图中可以看出，图2中存在多处毛刺很难彻底消除，而图3逼近于图2且是平滑的。消除了大量的毛刺后使求极值变得容易了许多，并随着n的增大，逼近程度会更好。

图1Lena灰度图像

图2Lena灰度直方图

图3Lena灰度直方图逼近的伯恩斯坦多项式曲线

2.5 伯恩斯坦多项式的极值

根据伯恩斯坦定理，可以将图像灰度直方图的峰谷值求解问题简化为伯恩斯坦一元n次多项式的极值求解问题，并且避开了直方图曲线上的大量毛刺干扰现象。

对式(2)的Bn(f,x)进一步求一阶导数，得到以下的Bn′−1(f, x)，Bn(f,x)函数的极值问题又简化为一元 n−1次多项式Bn′−1(f, x)所组成的方程的求根问题。

这里，因为最关心的是 x∈[a,b]情况下的求导结果，所以直接使用式(4)对Cn(f,x)函数求关于x的一阶导数即可。从而得出满足[a,b]区间的伯恩斯坦多项式的一阶导数

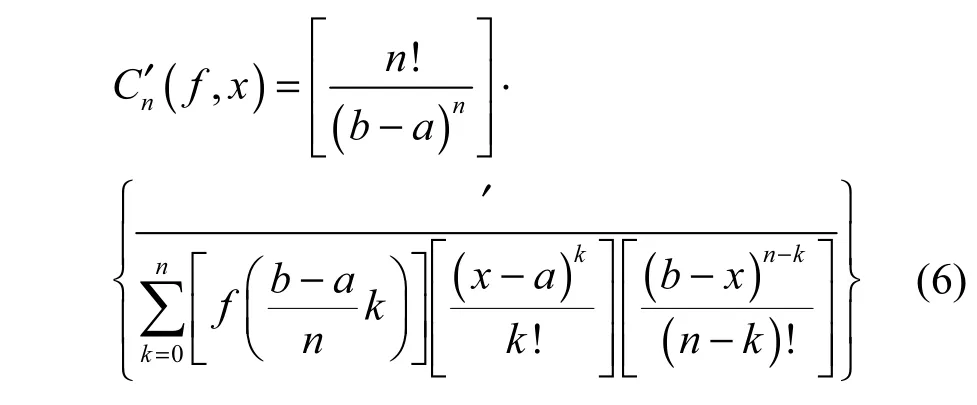
对式(6)中做进一步的推导简化后得式(7)。

式(7)中通项含有4个子项，已用中括弧标记出来，如果将第4子项，即设计为向量并先行计算，则整个式(7)对每个x（x∈[a,b]）来说的时间复杂度为O(n)。

2.6 伯恩斯坦多项式的极性

再次根据伯恩斯坦定理，为了判断曲线梯度的变化，对 Bn(f,x)进一步求二阶导数，得到以下的Bn′−2(f, x)，将Bn(f,x)函数的极值的极大、极小特性判定问题简化为一元 n−2次多项式Bn′−2(f, x)值的正负值判定问题，当为负时此处是原函数的极大点，为正时此处是原函数的极小点。

这里因为最关心的是 x∈[a,b]情况下的求导结果，所以直接使用式(7)对Cn′(f,x)数求关于x的一阶导数即可。从而得出满足[a,b]区间的伯恩斯坦多项式的二阶导数，做进一步的推导简化后得式(9)。式(9)中通项含有4个子项，已用中括弧标记出来，如果将第4子项，即设计为向量并先行计算，则整个式(9)对每个 x（x∈[a, b]）来说的时间复杂度为O(n)。

结合式(4)、式(7)和式(9)，可以求得伯恩斯坦多项式Bn(f,x)的值以及一阶、二阶导数的值，从而得到图像灰度直方图f(x)的n次逼近值以及极值和极大极小特性。

由2.2节可知，求解伯恩斯坦多项式极值的问题已经转换为求解伯恩斯坦多项式一阶导数方程根的问题，极值的特性问题已经转换为求解伯恩斯坦多项式二阶导数的问题，在一阶导数为零的情况下，如果二阶导数为负时，为极大值；否则为极小值。

根据以上的极值和极性的计算式，并使用第3节介绍的算法自动标注出恩斯坦多项式曲线上的全部极值点。对图3的极值求解，结果如图4所示。

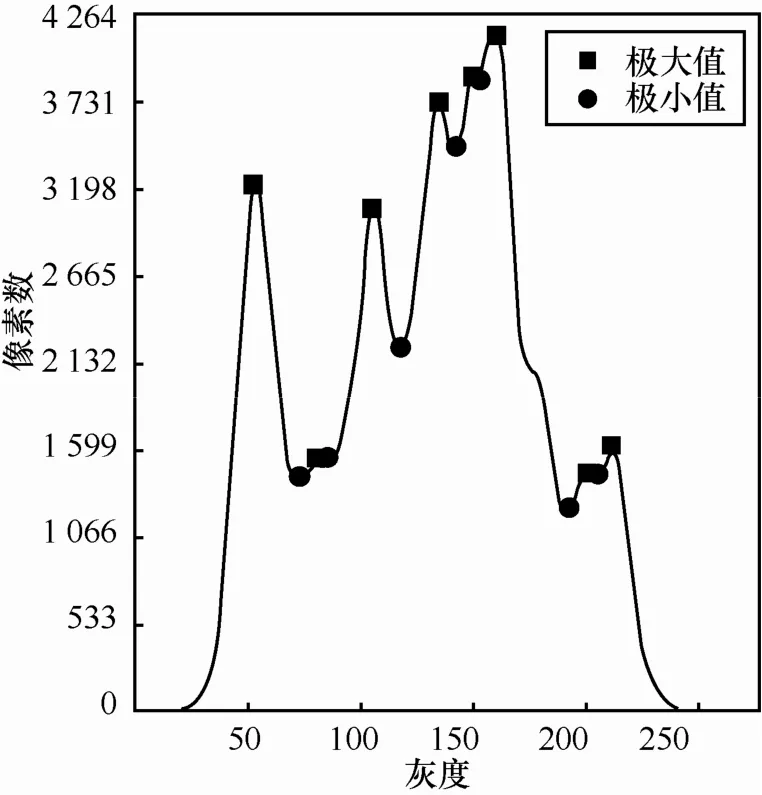
图4Lena灰度直方图逼近的伯恩斯坦图的极值

3 算法实现

3.1 伯恩斯坦多项式的求解算法

算法1伯恩斯坦多项式的求解算法

输入f(x)在[a,b]上的全部值以及n的值。

输出Cn(f,x) 在[a,b]上的全部值。

begin

步骤2取s=1; 对于(k=1;k≤n;k++)

步骤3对于(x = a; x≤b; x++) 计算以下值。

1) 取 v[n]=1；对于(k = 1; k ≤ n; k++) 计算v[n−k]= v[n − k + 1]的值。

2) 取 u = 1; Cn(f,x) = f[0]·u·v[0]; w=0;对于(k = 1;k ≤ n; k++)计算以下值：

② w=f[(kh)]·u·v[k];

③ Cn(f,x) = Cn(f,x)+ w。

3) 计算Cn(f,x) = Cn(f,x) s的值。

步骤4返回Cn(f,x) 的值。

end

3.2 伯恩斯坦多项式极值的求解算法

算法2伯恩斯坦多项式极值的求解算法

输入f(x)在[a,b]上的全部值以及n的值。

输出Cn(f,x) 在[a,b]上的全部值。

begin

步骤2取s=1; 对于(k=1;k≤n;k++)

步骤3对于(x = a; x≤b; x++) 计算以下值。

1) 取 v[n]=1；对于(k = 1; k≤n; k++) 计算 v[n −k]= v[n − k + 1]的值。

2) 取 u = 1; Cn(f,x)= (f[1·h]−f[0·h])·u·v[1]; w=0;对于(k = 1; k ≤ n−1; k++)计算以下值：

② w=(f[(k+1)h]−f[(kh)])·u·v[k+1];

③ Cn(f,x) = Cn(f,x) + w。

3) 计算Cn(f,x) = Cn(f,x) s的值。

步骤4返回Cm(f,x) 的值。

end

3.3 伯恩斯坦多项式极性的求解算法

算法3伯恩斯坦多项式极性的求解算法

输入f(x)在[a,b]上的全部值以及n的值。

输出Cn(f,x) 在[a,b]上的全部值。

begin

步骤2取s=1; 对于(k=1;k≤n; k++)

步骤3对于(x = a; x≤b; x++) 计算以下值。

1) 取 v[n]=1；对于(k = 1; k ≤ n; k++) 计算v[n−k]= v[n − k + 1]的值。

2) 取 u =1; Cn(f,x) = (f[2h]−2 f[1·h]+ f[0·h])·u·v[2];w=0；对于(k = 1; k ≤ n−2; k++)计算以下值：

② w=(f[(k+2) h]−2f[(k+1) h]+ f[(kh)])·u·v[k+2];

③ Cn(f,x)= Cn(f,x) + w。

3) 计算Cn(f,x) = Cn(f,x) s的值。

步骤4返回Cn(f,x) 的值。

end

算法1、算法2和算法3对于每一个x的时间复杂度都是O(n)。

通过算法 1得到了伯恩斯坦曲线在[a,b]上的值，通过算法2得到了伯恩斯坦曲线在[a,b]上的极值和极值点，通过算法3得到了伯恩斯坦曲线在[a,b]上的极性和极值点，从而获得伯恩斯坦曲线在[a,b]上的极大值、极小值和极值点，即对应直方图上的全部峰值和谷值的估算和近似值，再由3.4节的类k-means最小距离分类算法找到图像灰度直方图上的全部实际峰值和谷值。

3.4 多阈值的求解算法

本小节首先介绍距离空间和距离的定义，然后使用类k-means的最小距离分类算法求解灰度直方图的峰谷值，探测出图像的多个阈值，最后实施基于多阈值的图像分割。

1) 距离空间

定义1距离空间。设X为任意集合，如果对X上的任意2个元素x和y，都对应一个实数ρ(x,y)，并且满足以下3个条件：

① 非负性，ρ(x,y)≥0，其中，当且仅当 x=y时ρ(x,y)=0；

② 对称性，ρ(x,y)= ρ(y,x)；

③ 三点不等式，∀x，y，z∈X，都有 ρ(x,y)≤ρ(x,z) +ρ(z,y)。则称ρ(x,y)为x和y之间的距离，而称X为以ρ(x,y)为距离的距离空间。

具体应用时，对于不同的空间可以取不同形式的距离。比如，对于 n维欧式空间 Rn中的 2个n维向量 x= (ζ1, ζ2,… , ζn)和 y=(η1, η2,… , ηn)之间的距离定义如下

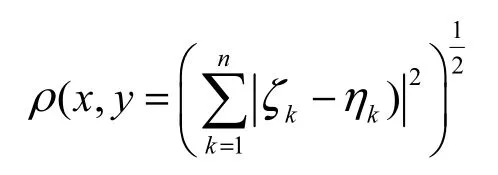
而对于空间C[a,b]中连续函数x(t)和y(t)之间的距离定义如下

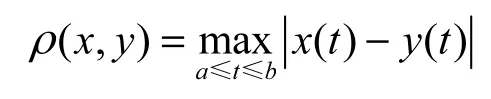
2) 类k-means最小距离分类算法

首先选定k个分类估算值center[k]，它们是伯恩斯坦多项式曲线上的极值点，然后在直方图曲线的对应点的一定距离范围（邻域）内，寻找直方图上的准极值点，将找到的点 data[n]不断去修正center[k]，直到满足要求为止，即可得到直方图上的峰谷点和峰谷值。

算法4类k-means最小距离分类算法

输入初始为k个分类和n个数据data[n];

输出k个分类中心点center[k];

begin

步骤1随机选择k个初始分类中心点center[k]，比如 center[0]=data[0], …, center[k−1]=data[k−1]。

步骤2将data[0], … ,data[n]分别与center[0], …,center[k−1]相比较，与center[i]差值最少者标记为i。

步骤3对于所有标记为 i的点，重新按照以下公式计算新的center[i]。

步骤4重复步骤2和步骤3，直到所有center[i]值的距离变化小于给定的阈值。

end

图5是经过类k-means最小距离分类算法得到的Lena灰度直方图的峰谷值，图6为对Lena图像进行多阈值分割后的结果，其中不同的目标以及背景分别采用不同的灰度来填充。

4 性能与结果比较

4.1 对于不同类物体的多阈值图像分割

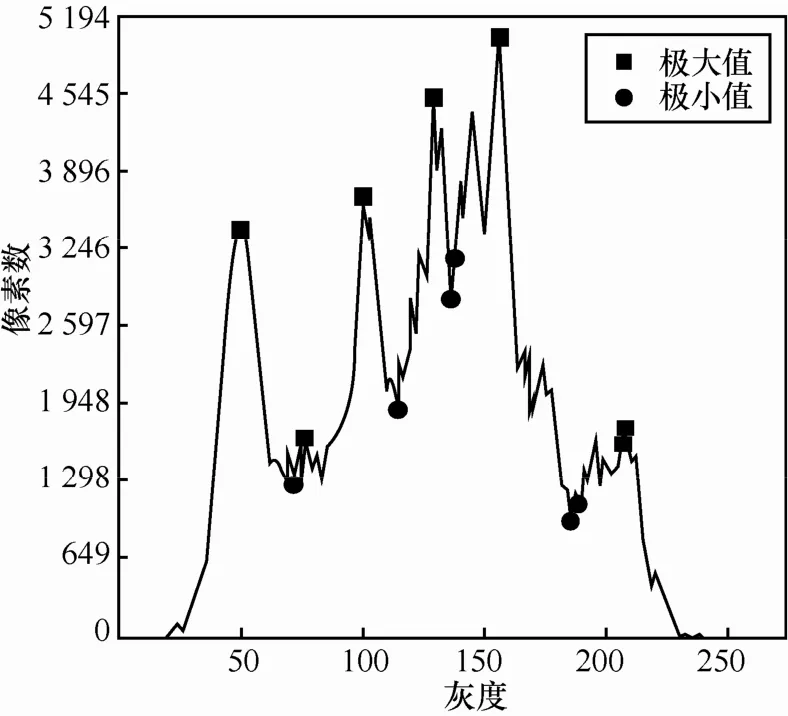
图5Lena灰度直方图的峰谷值

图6采用本文多阈值图像分割算法后的Lena图像

使用本文算法进一步对不同类的典型物体图像，比如apple、house、sky和vegetable等分别进行图像分割，这些图像的灰度直方图形状差异较大，而本算法都可以实施分割，效果如图 7所示，图中的分割结果用不同的灰度标识不同的目标以及背景。

4.2 与传统的阈值算法的性能比较

传统的几种求解阈值算法的一个共性问题是求解过程易受直方图噪声的影响，导致结果会有所偏差。对图像进行滤波平滑处理后可以部分消除这种噪声，但会丢失图像中的一些敏感信息。

针对Lena图，几种基于阈值的图像分割算法的性能比较如表1所示，结果比较如图6和图8所示。实验表明，双峰法、迭代法和Otsu法是单目标的；双峰法、迭代法、Otsu法和最大熵法的计算方向性不强，且都需要提前平滑滤波来消除噪声；Otsu法、最大熵法和本文算法的分割效果都比较理想，本文算法的步骤更简单、易实施、用时少、且效果依n可调，这里n=1200。

表1几种基于阈值的图像分割算法的性能比较

图8几种基于阈值的图像分割算法的结果比较

4.3 与最大熵法的结果比较

最大熵法和本文算法都是可以完成多阈值的分割算法，相比较而言，本文的算法因为不需要通过平滑滤波消除噪声，实施起来更简单，且保留图像的细节，用时非常少。2种算法的分割效果接近，都比较好。另外，本文算法还与样条算法进行了比较，性能和效果均比较明显。

5 结束语

本文提出的基于伯恩斯坦一致逼近多项式进行多阈值图像分割的算法，克服了以前一些算法的计算复杂、抗干扰差和不稳定等方面的缺点，充分利用伯恩斯坦多项式的许多优良性质，大大简化了阈值求解的步骤，整体上稳定，时间复杂度小，用时少，效率高，逼近性能和分割效果均好，因此实用性较强。

本文的算法可以用于水果质检抽查和送样方面的图像识别的前期预处理应用以及印制电路板焊点调试，也可用于视频系统中帧图像的压缩传送应用。当然本文的算法也有一定的局限性，仍需要进一步优化。比如收敛性较慢，当阶数n较小时，只能得到直方图的轮廓逼近曲线，会丢失部分局部细节；当提高阶数n到一定程度时，基本可以满足要求；而当进一步提高阶数n幅度时，逼近趋势变化不明显，可以采用的一种优化方案是使用切比雪夫多项式降阶，从而提高收敛速度。

[1]RAFAEL C, RICHARD E. Digital image processing second edition[M]. Publishing House of Electronics Industry, 2002: 567-642.

[2]程宏煌, 戴卫恒, 姚趁趁. 图像分割方法综述[J]. 电信快报, 2000,1(10): 39-41.CHENG H H，DAI W H，YAO C C．Image segmentation techniques[J]. Telecom Express, 2000, 1(10): 39-41．

[3]周鲜成. 图像分割方法及其应用研究综述[J]. 信息技术, 2007,1(12): 11-14.ZHOU X C. Study of image segmentation methods and their applications [J]. Information Technology, 2007, 1(12): 11-14.

[4]CHIN Y H, MON J W. Image segmentation[D]. Madison: University of Wisconsin- Madison, 2006.

[5]CHRISTIAN R，LOIC P，NASSIR N．Image segmentation in twenty questions[C]//CVPR2015, 2015.

[6]YATHARTH S. Algorithms for image segmentation [D]. Pilani: Birla Institute of Technology and Science, 2006.

[7]SHEN T Z, FANG Z W, WU L Y, et al. A new adaptive image segmentation method [J]. Journal of Beijing Institute of Technology, 1998,7(3): 316-321.

[8]王亮申, 欧宗瑛, 侯杰, 等. 基于遗传算法的最优直方图阈值图像分割算法[J]. 数据采集与处理, 2005, 20(2): 130-134.WANG L S, OU Z Y，HOU J, et al. Image segmentation based on optimal histogram threshold by improved genetic algorithms[J]. Journal of Data Acquisition amp; Processing, 2005, 20(2): 130-134.

[9]李哲学, 陈树越. 快速多阈值图像分割法[J]. 计算机应用, 2010,30(5): 1336-1343.LI Z X, CHEN S Y. Fast multi-thresholding approach [J]. Journal of Computer Applications, 2010, 30(5): 1336-1343.

[10]安丰玲, 梁德群, 王胜军, 等. 基于多阈值分割的图像区间均衡增强[C]//第十二届全国图像图形学学术会议. 2005: 15-19.AN F L, LIANG D Q, WANG S J, et al. Image region equalization enhancement based on multi-thresholds segmentation [C]//The 12th National Conference on Image and Graphics. 2005: 15-19.

[11]邢延超, 谈正. 基于多阈值融合的图像分割[J]. 计算机学报, 2004,27(2): 252-256.XING Y Q, TAN Z. Multi-threshold fusion based image segmentation[J]. Chinese Journal of Computers, 2004, 27(2): 252-256.

[12]曹增强, 范忠诚. 一种去除图像毛刺的快速算法[J]. 数据采集与处理, 1992, 7(3): 235-240.CAO Z Q, FAN Z C. An algorithm for fast eliminating image thorns[J]. Journal of Data Acquisition amp; Processing, 1992, 7(3):235-240.

[13]黄琴波.结合特定理论的图像分割方法[J]. 电子科技, 2010, 23(12):92-95.HUANG Q B. Survey on the methods of image segmentation research[J]. Electronic Sci. amp;Tech, 2010, 23(12): 92-95.

[14]许新征, 丁世飞, 史忠植, 等. 图像分割的新理论和新方法[J].电子学报, 2010, 28(2A): 76-82.XU X Z, DING S F, SHI Z Z, et al. New theories and methods of image segmentation [J]. Acta Electronica Sinica, 2010, 28(2A): 76-82.

[15]庞永锋, 杨威, 孙燕, 等. 应用泛函分析基础 [M]. 西安: 西安电子科技大学出版社, 2015: 89-118.PANG Y F, YANG W, SUN Y, et al. Fundamentals of applied functional analysis[M]. Xi’an: Xidian University Press, 2015: 89-118.

[16]蒋尔雄, 赵风光, 苏仰锋. 数值逼近：第2版 [M]. 上海: 复旦大学出版社, 2008: 96-136.JIANG E X, ZHAO F G, SU Y F. Numerical approximation: 2nd edition[M]. Shanghai: Fudan University Press, 2008: 96-136.

[17]程东旭, 杜娅丽. 基于样条插值的图像分割算法研究[J]. 中原工学院学报, 2015, 26(1): 9-12.CHENG D X, DU Y L. Image segmentation algorithm study based on spline interpolation [J]. Journal of Zhongyuan University of Technology, 2015, 26(1): 9-12.

[18]陈争光, 杨冬风, 冯晓娟. 三次样条在图像多阈值分割中的应用[J].黑龙江八一农垦大学学报, 2010, 22(5): 88-90.CHEN Z G, YANG D F, FENG X J. Application of cubic spline in image multi-threshold segmentation [J]. Journal of Heilongjiang Bayi Agricultural University, 2010, 22(5): 88-90.

[19]莫国瑞, 刘开第. 函数逼近论方法 [M]. 北京: 科学出版社, 2003: 1-28.MO G R, LIU K D. Function approximation theory method [M]. Beijing: Science Press, 2003: 1-28.

Multi-threshold algorithm about image segmentation based on polynomial uniform approximation

WEI Yan-jun1, FENG Bo-qin1, WU Wei-guo2
(1. Computer Teaching amp; Experiment Centre, Xi’an Jiaotong University, Xi’an 710049, China;2. Department of Computer Science amp; Technology, Xi’an Jiaotong University, Xi’an 710049, China)

Aiming at those shortcomings of previous multi-threshold image segmentation algorithm such as large complexity and instability caused by the image histogram glitch interference, a new multi-threshold image segmentation algorithm was proposed using Bernstein polynomial to uniformly approximate histogram curve. First, according to the approximation theory of Weierstrass to construct Bernstein polynomial for the histogram curve, then more difficult peak value calculating of the histogram was reduced to the Bernstein polynomial extremal generating, that was exported easily by the first and second derivative of Bernstein polynomial function, and finally obtain the actual peak value of the image histogram by picking up these extremes and polar values and filtering through classification algorithm, and finish multi-threshold image segmentation. Experimental results show that the algorithm is insensitive for histogram glitch interference, the overall is stable, the redundant computation and time complexity are smaller, with less time and high efficiency, the approximate performance and segmentation effect are better.

image segmentation, image histogram, threshold, uniform approximation, Bernstein polynomial, distance space

s:The National Natural Science Foundation of China (No.91330117), The National High Technology Research and Development Program of China (863 Program) (No.2012AA01A306)

TP309

10.11959/j.issn.1000-436x.2016196

2016-06-15；

2016-08-31

国家自然科学基金资助项目（No.91330117）；国家高技术研究发展计划（“863”计划）基金资助项目（No.2012AA01A306）