基于亲和传播的动态社会网络影响力扩散模型

2016-11-24陈云芳夏涛张伟李晋

通信学报 2016年10期

关键词：级联因数静态

陈云芳，夏涛,2，张伟，李晋

（1. 南京邮电大学计算机学院，江苏南京 210003；2. 中国电信济宁分公司，山东济宁272000；3. 北京信息科技大学公共管理与传媒学院，北京 100192）

基于亲和传播的动态社会网络影响力扩散模型

陈云芳1，夏涛1,2，张伟1，李晋3

（1. 南京邮电大学计算机学院，江苏南京 210003；2. 中国电信济宁分公司，山东济宁272000；3. 北京信息科技大学公共管理与传媒学院，北京 100192）

影响力最大化模型研究是近来社会网络的一个热点问题，然而传统的独立级联模型以静态网络中为基础，且激活概率一般设定为固定值。提出一种加入衰减因数的动态社会网络影响力扩散模型—DDIC模型，其采用亲和传播来计算节点之间的激活概率，依据时间片对社会网络进行动态切分，使激活概率在不同时间片中实现了有效关联。实验结果表明DDIC模型中种子节点有更多机会激活它的邻居节点，且采用亲和传播计算出的影响力值能更准确地体现DDIC模型的传播过程。

动态社会网络；影响力扩散；亲和传播

1 引言

虚拟社会所形成的人际关系网络以及各种各样的社会网络越来越多地出现在人们面前，通过这些社会网络所表现出来的社会以及人际关系互动是许多领域的研究热点。在社会影响力传播中，社会网络作为传播的媒介，在个体之间相互影响、个体之间传播观点与信息等方面发挥着巨大的作用。一条信息可以在人群中迅速地蔓延，也有可能在很短时间内就消失。了解信息被人们所接受的程度是很有必要的，这就需要了解信息是如何在社会网络中动态传播的，即人们在何种程度上能够受到好友的影响而去做某件事情，“口碑效应”在什么程度下会发生。

影响力最大化模型研究是近来社会影响力领域的一个热点问题。“病毒式营销”开始只是针对为数不多的几个相对于其他个体具有“影响力”的个体。将一种商品首先推荐给这样的群体，然后在人群中进行扩散，大多数个体会把此商品推荐给朋友，通过口口相传使这种商品得到推广。这种首先找到一定个数的具有“影响力”的节点，然后通过这些具有“影响力”的节点去影响别的节点的问题被称为影响力最大化问题。

关于影响力最大化问题的研究大多都是在静态网络上展开。然而，网络本身是动态的，其中的个体和它们之间的交互会随时间的推移而变化。相比于动态网络，静态网络损失了节点之间的交互信息，不能很好地适应网络的变化情况。因此，研究在动态网络中进行影响力最大化模型的扩散很有必要。

2 相关工作

2002年，Richardson等[1]将影响力最大化问题引入到社会网络领域后引起了众多学者的关注。Kempe等[2]在 2003年第一次比较系统地研究了影响力最大化模型，其总结了影响力最大化模型：独立级联（IC, independent cascade）模型和线性阈值（LT, linear thresholds）模型，并且证明了独立级联模型、线性阈值模型是NP难题，同时证明了2个模型的扩散结果函数是一个子模函数，满足收益递减原则。

自从影响力模型提出以后，许多文献都是围绕着怎么找到影响力最大化问题中的种子节点来研究的。这部分算法大体上可以分为2类：贪心算法和探索式算法。贪心算法由Kempe等提出，许多文献对贪心算法进行了改进：Leskovec等[3]提出的CELF算法运用了影响力最大化问题的子模特性，很大程度上降低了评价节点影响力；Chen等[4]提出了NewGreedy算法和MixGreedy算法。贪心算法的高时间复杂度使其在大型网络的应用受到了限制，另一种可能的方法就是使用探索式算法。在社会网络分析中，度和一些其他的基于中心性的探索式算法经常被用来评价节点的影响力。在影响力最大化问题中节点度经常被用来选择种子节点，文献[2]的实验选择具有最大度数的节点为种子节点，能够比其他探索式算法得到更好的效果。以往文献都没有考虑网络中的社区结构特性。Galstyan等[5]第一次提出了一种基于社区结构的影响力最大化问题的解决方案，但是该方法只是局限于2个连接稀疏的社区网络，而实际中的网络一般包括很多社区网络。Cao等[6]把影响力最大化问题转化为最佳资源分配问题，将整个网络根据社区发现算法划分为若干个社区；然后将数个节点按照最佳资源分配问题的解决方法分配给每个社区节点；每个社区根据分配的节点利用影响力最大化模型来找到种子节点。

关于节点之间边的影响力分析也有很多文献进行了相关研究，Saito等[7]在研究信息传播的独立级联模型时讨论了这类问题，将影响力模型转化成了一种最大似然问题进行求解。因为该模型每次迭代过程都要对每条链接上的影响力系数进行计算，时间复杂度较高，所以并不适合大规模社交网络中的影响力度量。Barbieri等[8]在Saito等的基础上讨论了多个主题下的影响力最大化模型，其采用了最大似然估计。以上这些方法都是基于网络中的节点以往的行为进行的估计。Tang等[9]提出了基于主题的社会影响力分析的一种方法——TAP（topical affinity propagation）算法。该算法是一种亲和传播[11]聚类算法，首先使用隐藏狄利克雷模型（LDA）将合著者网络进行主题分布，然后使用亲和传播方法分析节点间不同主题之间的影响力。相比于以往的算法，TAP算法求解主题间的影响力比较简单可行，而且可以定量地分析节点间的影响力。

无论是基于节点还是基于边的影响力分析，上述影响力最大化问题的研究都是在静态网络中进行扩散的，然而网络本身是动态的，其中的个体和它们之间的交互随时间的推移而变化。Habiba等[10]提出了一种在动态网络中进行影响力最大化问题扩散的模型，该模型将在每个时间片中进行一次扩散，上一个时间片的激活节点作为下一个时间片的初始激活节点进行扩散，直到最后一个时间片或者没有新的被激活节点时，扩散过程结束。然而，上述模型中的每个时间片是相互独立的，没有考虑到时间片之间影响力的联系，并且，模型中将影响力值设置为同一个值，很显然是违背实际情况的。

综上所述，社会网络是动态的，影响力的传播在时间片中的激活概率也不是一成不变的。为此，本文提出一种加入衰减因数的动态网络独立级联（DDIC，decay dynamic network independent cascade）模型。本文工作主要体现在2个方面：1) 影响力在某个时间片中建立以后，在后续的时间片中如果这2个节点依然存在连接，那么这2个节点之间的影响力不应该只考虑这个时间片中的影响力，需要考虑以前影响力的累加，针对这个问题 DDIC模型引入衰减因数；2) 在社会网络中由于存在着个体差异，个体之间的影响力不会是相同的，针对这个问题，DDIC模型中个体之间的影响力采用亲和传播的方法来计算节点之间的影响力值。

3 动态网络中影响力扩散问题

3.1 动态网络

静态网络独立级联模型都是基于一种合成网络来进行扩散的，这种合成网络展现了在一定的时间内所观察到的全部个体和个体之间的交互。这种网络只能展现一段时间内所有个体之间交互的叠加，并不能反映出节点和边出现的时序信息。

动态网络是由有限个静态网络按照一定的时间序列构成的一组网络。其中，每一个静态网络是网络中所有个体以及个体之间相互交互的在某个时间的一个快照。动态网络描述了在一段时间内网络的演化过程。如图1所示，上半部分前3个图表示了从时间序列T1到时间序列T3节点A至节点E之间的相互联系，最后一个图是时间片T1、T2、T3合成的静态网络，下半部分的图也是一样的。由图1可以看出，节点A至节点E在2个部分时间片T1、T2、T3中边是不同的，而合成的静态网络是一样的。由此，可以清晰地看出合成静态网络会损失网络演化中的时序信息。

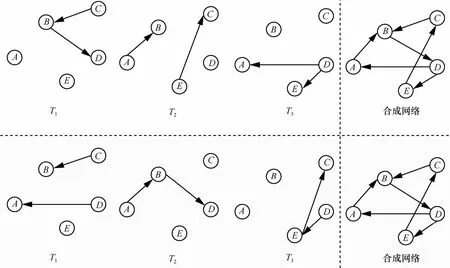
图1基于时间片的网络与静态网络

3.2 加入衰减因数的动态网络独立级联模型

DDIC模型中的节点状态采用与静态网络中的节点状态一致的方式，也具有2种状态：激活态和未激活态，每个节点的状态只能从未激活态转为激活态而不能反转。

在DDIC模型中，首先输入的是种子节点集合A0∈I。在加入衰减因数动态网络中每个已经激活的节点vt在时间序列t的网络中去尝试激活它的未被激活的邻居节点wt，wt是否被激活取决于vt和wt之间的影响力概率。

在DDIC模型中激活概率定义如下：如果在时间片t−1中节点v和节点w有链接，而在时间片t中，节点v和节点w也有链接时，那么在时间片t中节点v和节点w之间的激活概率为

如果当wt有多个邻居节点处于激活状态时，这些激活节点对wt的影响是随机的、独立的。如果在时刻t的网络中vt成功地把它的邻居节点wt激活，那么在下一个时间片中不管vt+1和wt+1之间是否存在边(vt+1,wt+1)∈Et+1，wt+1都是具有影响力的节点。如果在时间序列t的静态网络中vt没有将wt成功激活，那么在以后的时间序列中，如果vT和wT中存在边(vT, wT)∈ET，vT将尝试激活wT。如果整个扩散过程没有新的被激活节点或者扩散已经达到最后一个时间片，那么扩散结束。

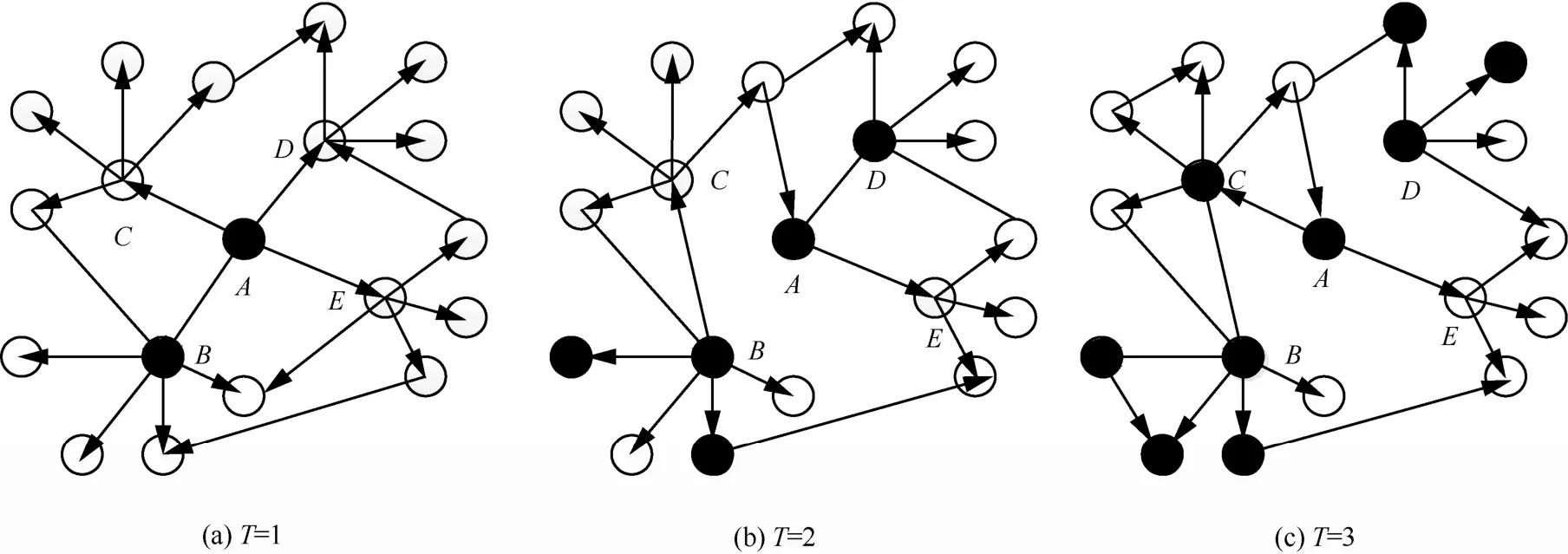
图2基于时间片网络的独立级联模型

图2简单描述了DDIC模型的过程，开始选择节点A为种子节点，在T=1的网络中节点A激活了它的邻居节点B。在T=2的网络中节点A又激活了它的邻居节点D，此时节点A和节点B中已经没有了边，而节点B一样具有影响力并且激活了它的2个邻居节点。在T=3的网络中种子节点A和它的邻居节点C又重新连接，并且节点A成功激活了节点C。

DDIC模型可以分为2个步骤来理解。1) 对于每个时刻对应的静态网络采取“抛硬币”来确定网络中对应的节点间的通路边。节点v和节点w在时刻t的边概率值pvtwt表征了这个边在多大程度上能够被选为通路边，图3简单描述了图2的3个时间序列的时间片网络通过“抛硬币”的方式产生的通路边。2) 选择合适的节点作为模型开始的种子节点也就是那些能够使更多的节点被激活的节点。首先在T=1的静态网络中种子节点进行扩散，此时的扩散就是根据步骤1)找到的通路边进行的扩散，如果种子节点的邻居节点与种子节点之间有通路边，该邻居节点就会被激活。在T=1的静态网络中扩散后已经处于激活态的节点集合作为T=2的静态网络的种子节点，按照同样的方法在T=2的静态网络中进行扩散，重复这一过程直到模型结束，最终得到的节点集合为最后一个时间序列中激活的节点总数。

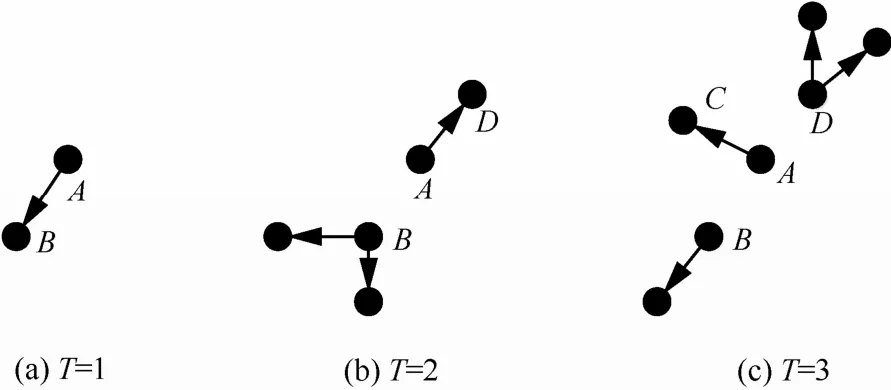
图3基于时间片网络的通路边

Kempe等证明了静态网络中的独立级联模型是一个NP难题。静态网络中的独立级联模型相当于在同一个时间序列网络中展开的，而加入衰减因数的动态网络独立级联模型在每个时间序列中的扩散过程和在静态网络中的扩散过程是一样的。所以，加入衰减因数的动态网络独立级联模型也是一个NP难题。Kempe等证明了对于应用静态网络中独立级联模型的任意实例，影响力结果函数具有子模特性。对于基于时间片网络的独立级联模型来说，影响力结果函数也具有子模特性。

3.3 基于亲和传播的激活概率

独立级联模型在进行影响力的扩散时节点间的激活概率为了简化模型统一设置成 0.01或其他的一个定值，这显然是不符合现实情况的，在现实中每个人对他的朋友的影响程度是不同的。

本节对TAP算法进行了改进，使节点相似性函数只涉及单个主题，具体如式(2)所示。

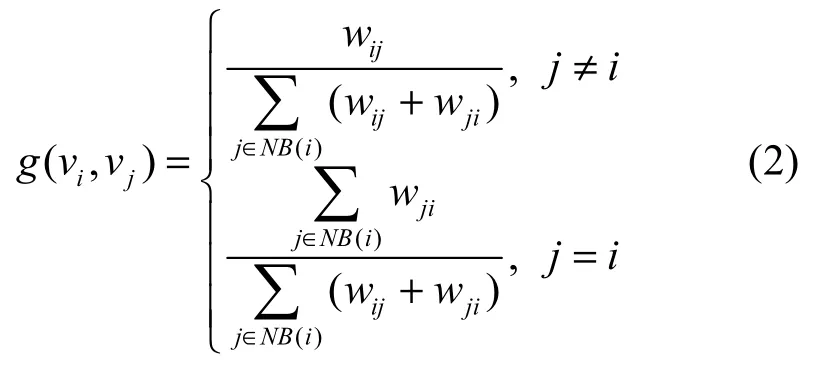
其中，NB(i)表示节点i的邻居节点集合，wij表示节点i到节点j的边的权重值，这个权重值的定义可以有多种形式，如在通话记录网络中可以定义为节点i和节点j之间的通话时长。式(2)可以解释为：如果节点 vi和节点 vj之间有较高的相似性或者权重，那么节点vi和节点vj之间有比较大的影响力；如果节点vi的邻居节点都认为节点vi对自己有较高的影响力，那么节点vi对自己具有较大影响力是有信心的。

对节点相似性函数g(vi,vj)进行对数归一化得到相似性矩阵。

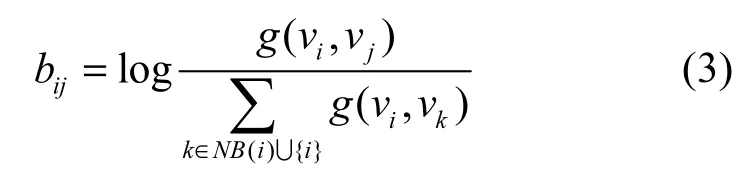
其中，bij表示节点j和节点i之间的特征函数值与节点i的所有邻居节点的特征函数值的比值，这个比值越大说明在节点i的邻居节点中节点j相对于其他节点对节点i越有影响力。

TAP算法利用因子图理论推导出了基于主题的亲和传播影响力算法的更新规则，在此基础上对更新规则做了调整使更新规则只在一个主题内展开，即不考虑主题的影响。

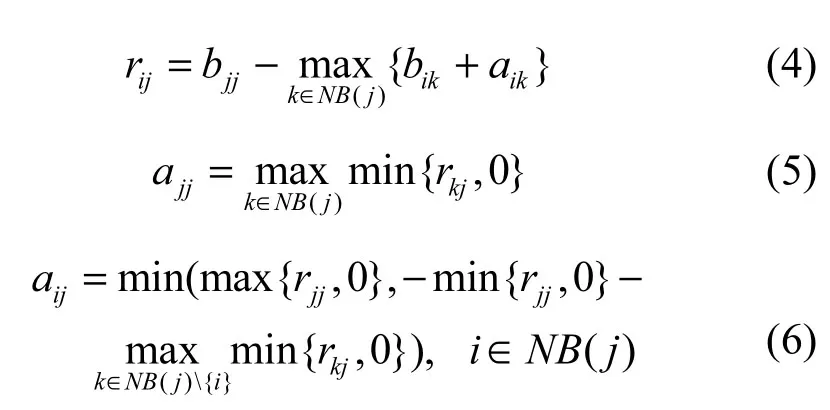
更新规则r表示了节点i对节点j对其有影响的积累证据。更新规则a表示节点j认为自己可以影响节点i的积累证据。

更新规则a和r说明了节点j对节点i的影响力，而对于一个社会网络图希望得到的影响力概率值是一个介于[0,1]之间的值pij，并且表示节点i对于节点j的影响程度，所以定义为

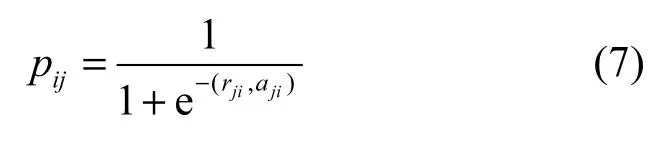
算法1基于亲和传播的激活概率算法

输入社会网络图G(V, E)

输出节点间的影响力概率值

1) 计算节点间特征函数值(vi, vj) //计算节点间的相似性值

2) 计算bij//根据式(3)计算bij的值

3) 初始化所有rij←0//初始化所有rij的值为0

4) Repeat //进行迭代计算

5)for eijdo

6) 更新 rij；//根据式(4)计算 rij的值

7)end

8)for vjdo

9) 更新 ajj；//根据式(5)计算 ajj的值

10)end

11)for eijdo

12)更新 aij；//根据式(6)计算 aij的值

13)end

14) until convergence//直到收敛

15) for eijdo

16)计算 pij； //根据式(7)计算 pij的值

17) end// pij为计算出的节点间影响力

4 实验分析

实验采用“9·11事件”的数据集，该数据集一共包含400个节点以及这400个节点之间相互联系的10个时间片。在每个时间片中，如果2个人之间有电话联系，那么2个人之间就会有一条边且通话时长为边的权重值。每个时间片中所含有的边数如表1所示。本文一共进行了3组对比实验，分别是：静态网络和动态网络中的独立级联模型与DDIC模型贪心算法对比；动态网络与加入衰减因数的动态网络独立级联模型3种算法对比；激活概率设置为固定值0.04与亲和传播概率对比。在实验中设定模拟传播次数R为100次，为了简化计算将衰减因数α的值设置为0.5。

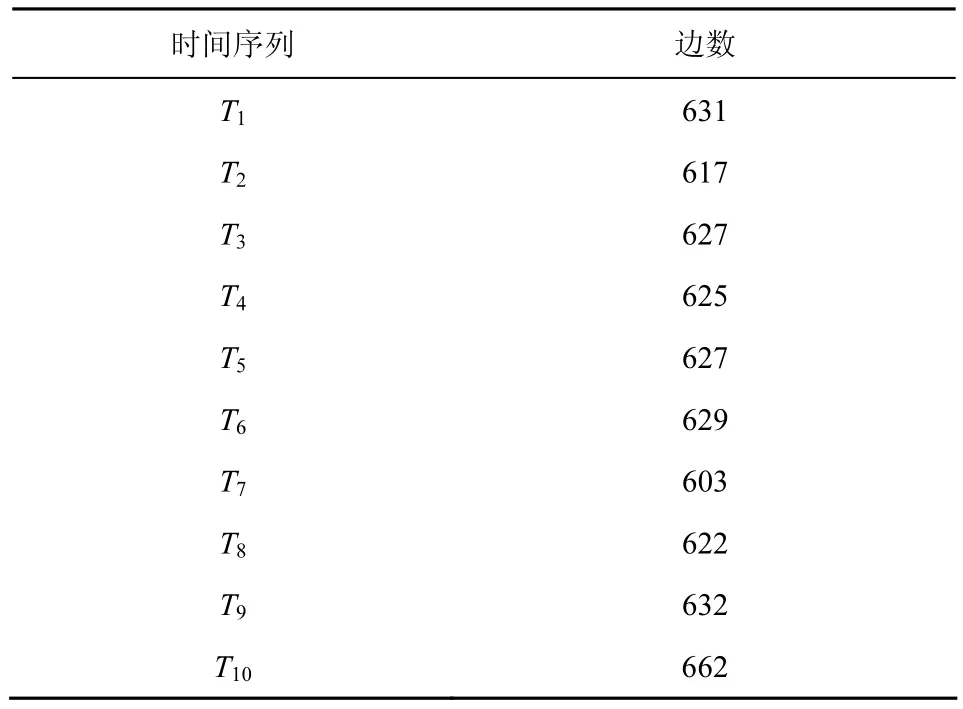
表1每个时间片中所含有的边数

4.1 静态网络与DDIC模型使用贪心算法的对比

该实验选择3种网络：T1时间片网络、10个时间片合成的静态网络、加入衰减因数的动态网络。图4(a)表示了在3种网络中使用贪心算法最终的激活节点数目进行对比。可以看出，在加入衰减因数的动态网络中独立级联模型中激活的节点数目比在单一的时间片中以及合成静态网络中激活的节点数目要多很多，这主要是因为在静态网络中每个节点只有一次机会去激活它的邻居节点，而在加入衰减因数的动态网络中一个节点，可以有多次机会去激活它的邻居节点，所以加入衰减因数的动态网络激活的节点数目要比静态网络中激活的数目多。

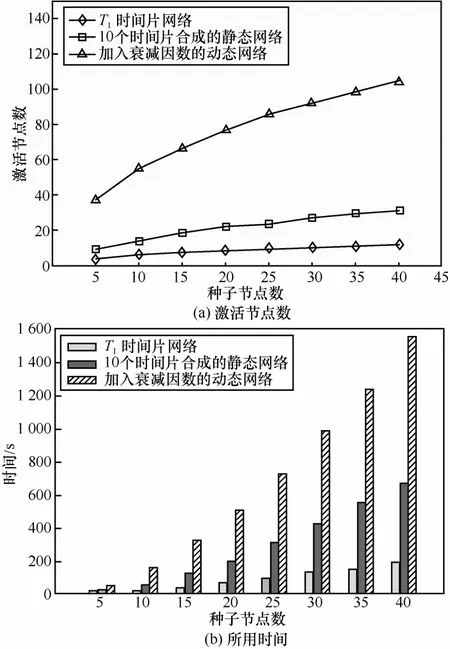
图43种网络中使用贪心算法进行扩散对比

图4(b)表示了在3种网络中使用贪心算法最终的所用时间对比。可以看出，在加入衰减因数的动态网络中，使用贪心算法进行确定种子节点集比在静态网络中使用贪心算法确定种子节点集所用的时间要长。这是因为在静态网络中一个节点只有一次机会去影响它的邻居节点，所以整个扩散过程一般在扩散 3轮左右就可完成，而在加入衰减因数的动态网络中一个节点有多次机会去激活它的邻居节点，所以激活的节点数目多，整个扩散过程比较长，一般要扩散 7轮左右才可以结束扩散过程，而贪心算法要进行 100次的模拟传播。所以这样加入衰减因数的动态网络在使用贪心算法进行确定种子节点的传播中要比静态网络所使用的时间要长。

由图4还可以看出，在合成静态网络中的激活节点数目和所用时间都比在一个时间片中要大，这是因为合成的网络中的边比单一的时间片网络要多，所以激活节点的数目要多。

4.2 贪心算法、NewGreedy算法、HT算法在DDIC模型中扩散的情况

该实验选择文献[4]中提出的 NewGreedy和文献[8]提出的HT算法与贪心算法进行对比。由于DDIC模型和静态网络中的独立级联模型一样都是 NP难题，同时都具有子模特性，贪心算法以及改进后的贪心算法同样能够在DDIC模型中使用。

如图5(a)所示，在加入衰减因数的动态网络中使用贪心算法、NewGreedy算法、HT算法以及随机选择算法（在400个节点中随机选择n个节点作为种子节点集）对独立级联模型进行种子节点集的确定的结果对比。由图5(a)可以看出，在准确率上，贪心算法和NewGreedy相差不大，而HT算法表现比前面2种算法要稍差一些，这是因为HT算法在进行种子节点确定的时候是基于去边的方法，这种方法会损失掉很多边所以造成结果不准确。而随机选择算法的结果会出现震荡，因为通过随机数的方法找的点是不可靠的。图5(b)表示了3种算法及随机选择算法所用时间对比，可以看出贪心算法所用的时间是最长的，比NewGreedy和HT算法要长很多，其次是NewGreedy算法，最好的是HT算法。因为随机选择算法比前3种算法所用时间少很多，故在图5(b)中不能表现出来。

在静态网络中也同样做了这 3个算法的对比，得到的结果和在加入衰减因数的动态网络上的结果是一致的。可以得出结论：贪心算法在静态网络和基于时间片网络中确定种子节点集是准确的，但是由于时间复杂度太大，贪心算法不适合节点和链接较多的网络；NewGreedy在2种网络中确定种子节点集时准确程度和贪心相差不大而且具有较小的时间复杂度，适合在大型网络中使用；HT算法虽然有较好的时间复杂度，但结果的准确性稍差一点。

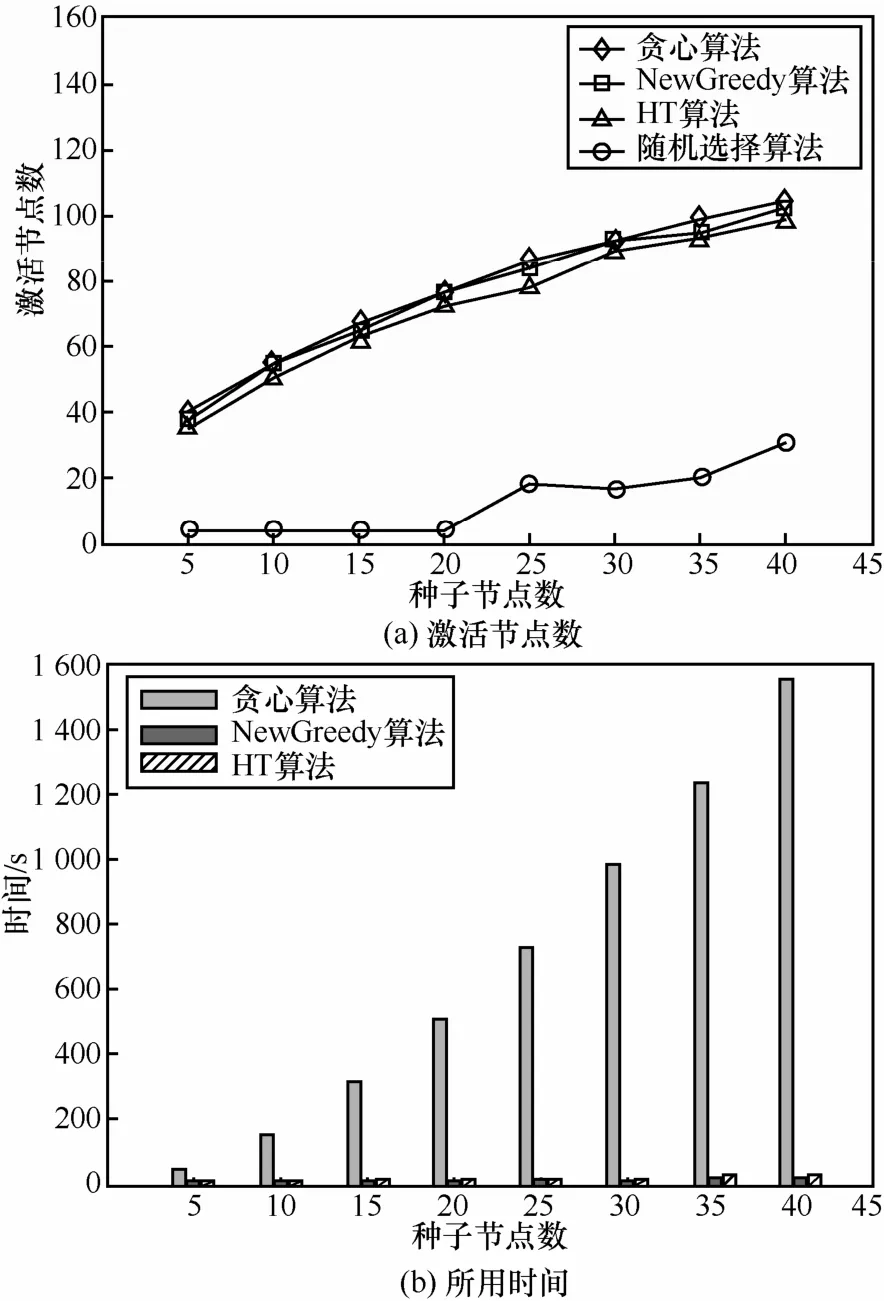
图5在加入衰减因数动态网络中3种算法及随机选择算法的对比

4.3 亲和传播的比较分析

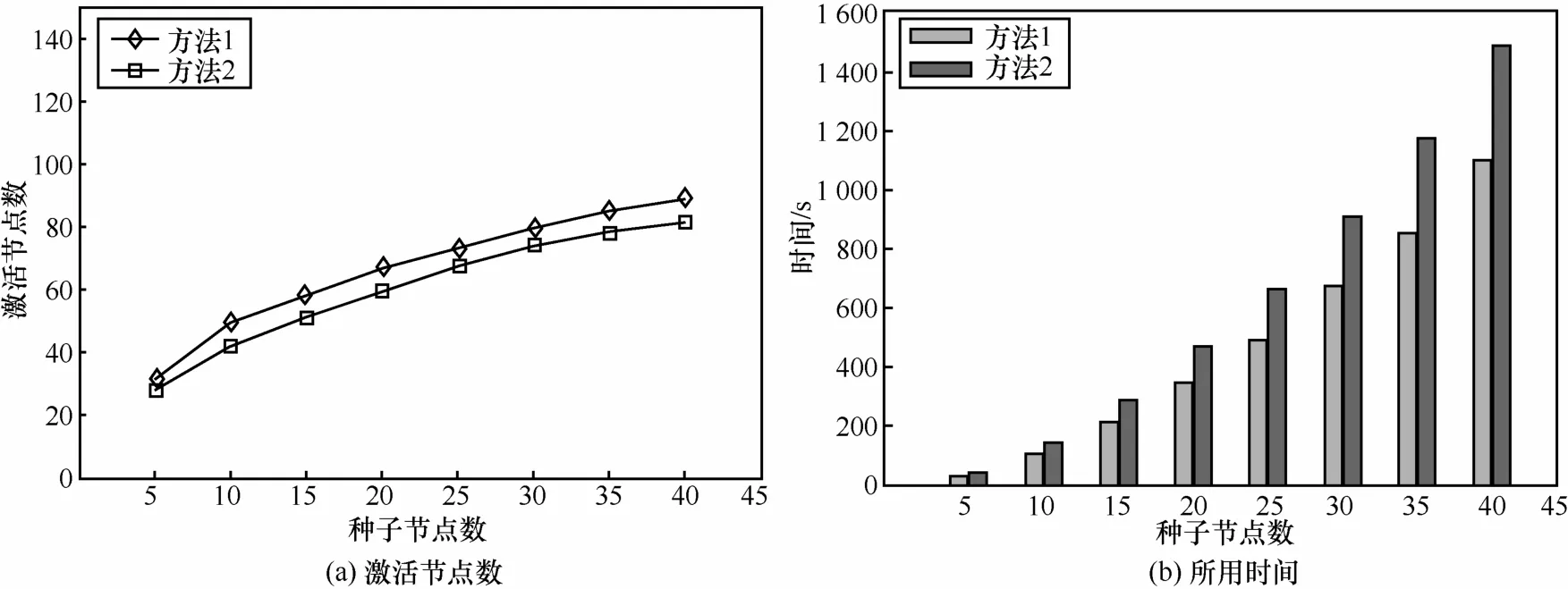
图6在DDIC模型中2种设定激活概率方法进行扩散的对比

在DDIC模型使用固定激活概率和使用亲和传播的影响力之间的结果对比，该实验中分别对2种节点间激活概率值的设定方法进行实验对比。其中，方法1是将节点间的激活概率统一设置为平均概率值0.04，方法2是使用亲和传播求出的概率值作为节点间激活概率值，如表2所示，在这部分实验中使用贪心算法来确定种子节点集。

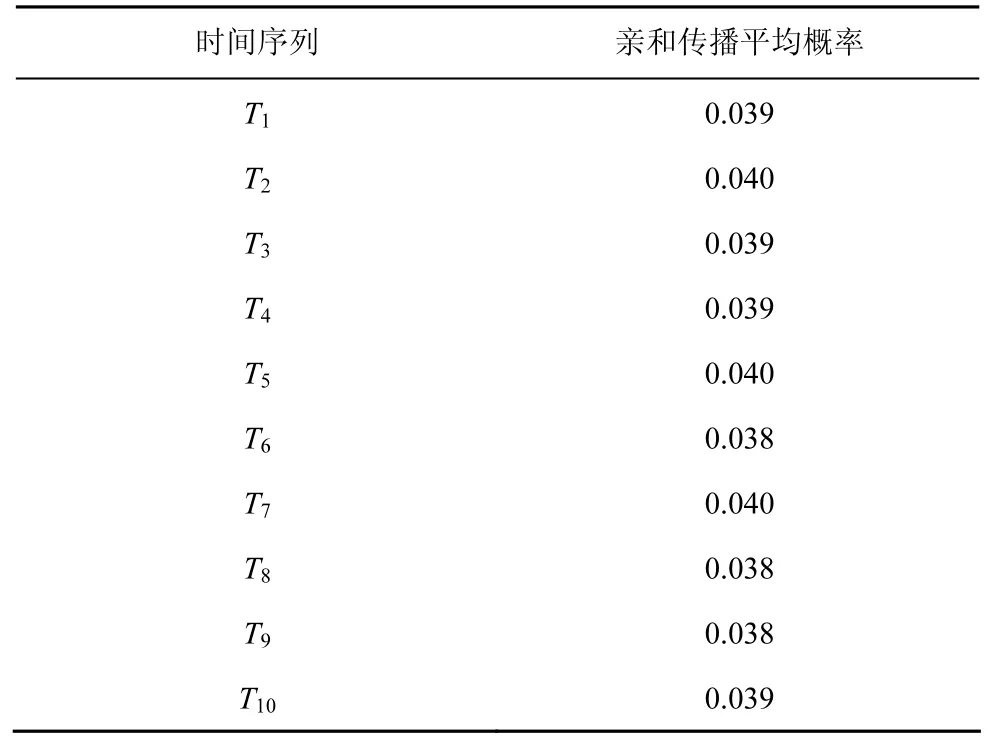
表2亲和传播概率的平均值

表3为在DDIC模型中用2种方法所确定的排名前20的影响力节点，通过对比可以发现2种方法所找到的节点的排名是不一样的。

图6所示为DDIC模型中2种设定激活概率进行扩散的对比，可以看出在激活概率设定为0.04的扩散结果中，激活节点数目要比使用亲和传播影响力概率值所激活的节点数目多，这可能是因为使用亲和传播所求出的一部分影响力是大于平均影响力0.04，而大部分影响力是低于0.04，这样造成了第一种方法要比第二种方法所激活的节点数目多。而且，使用亲和传播求出的概率值是根据边与边的权重值计算出来的相邻节点之间的影响力概率值，比统一设置成 0.04能更加准确地表现出DDIC模型的传播过程。

表3在DDIC模型中用2种方法所确定的排名前20的影响力节点

5 结束语

本文以独立级联模型为基础，研究了独立级联模型在动态网络中的扩散问题，并且提出了加入衰减因数的独立级联模型。与传统的动态网络中的独立级联模型不同，本文提出的加入衰减因数的独立级联模型 DDIC将动态网络中各时间片之间的影响力关联起来，并采用亲和传播来计算相邻节点之间的影响力概率值，使模型更能贴近真实的社会网络影响力的传播。本文通过对比实验可以得到以下结论：加入衰减因数的独立级联模型中由于每个节点有多次机会激活它的邻居节点，所以比静态网络中激活的节点数目要多；DDIC模型由于引入衰减因数使平均激活概率比不引人衰减因数的动态网络要高，所以激活的节点数目也多；在静态网络中适用的贪心算法在 DDIC模型中也同样适用；在 DDIC模型中采用亲和传播计算节点之间的影响力与将影响力值设置为固定值所得到的种子节点是不同的，亲和传播能更好地体现出DDIC模型的传播过程。

[1]RICHARDSON M, DOMINGOS P. Mining knowledge-sharing sites for viral marketing[C]//KDD '02 Proceedings of the Eighth ACM SIGKDD International Conference. 2002: 61-70.

[2]KEMPE D, KLEINBERG J M, TARDOS A. Maximizing the spread of influence through a social network[C]//The 9th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. 2003: 137-146.

[3]LESKOVEC J, KRAUSE A, GUESTRIN C. Cost-effective outbreak detection in networks[C]//The 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2007: 420-429.

[4]CHEN W, WANG Y, YANG S. Efficient influence maximization in social networks[C]//Proceedings of the 15th ACM SIGKDD International Conference. 2009: 199-208.

[5]GALSTYAN A, MUSOYAN V, COHEN P R. Maximizing influence propagation in networks with community structure[J]. Physical Review E Statistical Nonlinear amp; Soft Matter Physics, 2009, 79(2): 711-715.

[6]CAO T Y, WU X D, WANG S, et al. OASNET: an optimal allocation approach to influence maximization in modular social networks[J].ACM Symposium on Applied Computing, 2010: 1088-1094.

[7]SAITO K, NAKANO R, KIMURA M. Prediction of information diffusion probabilities for independent cascade model[J]. Knowledge-Based Intelligent Information and Engineering Systems Lecture Notes in Computer Science, 2008: 67-75.

[8]BARBIERI N, BONCHI F, MANCO G. Topic-aware social influence propagation models[J].Knowledge and Information Systems, 2013:2012,37(3): 81-90.

[9]TANG J, SUN J M, WANG C. Social influence analysis in large-scale networks[C]//The 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2009: 807-816.

[10]FREY B J, DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976.

[11]HABIBA T W B, BERGER-WOLF T Y. Maximizing the extent of spread in a dynamic network[J].Technical Report 20. DIMACS, 2007.

Influence diffusion model based on affinity of dynamic social network

CHEN Yun-fang1, XIA Tao1,2, ZHANG Wei1, LI Jin3
(1. School of Computer Science and Technology, Nanjing University of Posts and Telecommunications, Nanjing 210003, China;2. Jining Branch of China Telecom., Jining 272000, China;3. School of Public Administration and Communication, Beijing University of Information Science and Technology, Beijing 100192, China)

Recently, influence maximization model is a hot issue in the field of social network influence, while the traditional independent cascade model is generally based on static network with a fixed value of activation probability. DDIC model, which was a dynamic network influence diffusion model with attenuation factor was proposed. It calculated the activation probability between nodes via affinity propagation, and according with dynamic segmentation of social network time slice, calculation of influence on proliferation of next time slice with the current time slice of activation probability performance decay. The experimental results show that the nodes in the DDIC model have more chances to active the neighbor and the average probability of activing of the DDIC model is higher. Further experiments show that influence value via computing with affinity propagation can reflect the process of the spread model more accurately.

dynamic social network, influence diffusion, affinity propagation

s:The National Natural Science Foundation of China (No.61272422), Humanistic and Social Science Research Plan Project of Beijing Municipal Education Commission (No. SM201411232005)

TP393

10.11959/j.issn.1000-436x.2016194

2015-09-08；

2016-08-29

国家自然科学基金资助项目（No.61272422）；北京市教育委员会人文社会科学研究计划面上基金资助项目（No.SM201411232005）