线性离散一致性系统均方偏差上界

2016-11-24窦全胜厉玉蓉姜平

通信学报 2016年10期

关键词：均方线性一致性

窦全胜，厉玉蓉，姜平

(1. 山东工商学院计算机科学与技术学院，山东烟台 264005；2. 山东省车联网工程技术中心，山东烟台 264005)

线性离散一致性系统均方偏差上界

窦全胜1,2，厉玉蓉1，姜平1

(1. 山东工商学院计算机科学与技术学院，山东烟台 264005；2. 山东省车联网工程技术中心，山东烟台 264005)

一致性问题是多智能体协同控制的基础，有广泛的应用背景。之前的研究已经给出了线性一致性协议实现均方一致的充分条件，在此基础上，对线性离散均方一致性问题进行了更加深入的讨论，以图论和随机分析为基础，进一步给出并严格证明线性离散均方一致性问题噪声偏差的上界，同时以4种不同的网络拓扑为例，对所提理论结果进行了说明。结论将为线性离散一致性系统的噪声估计和控制提供理论依据。

群体智能；多智能体系统；一致性协议；噪声问题；均方一致性

1 引言

所谓多智能体(multi-agent)一致性问题是指在多智能体系统(MAS, multi-agents system)中，智能体通过与相邻智能体的信息交换来修订自身状态，最终达成所有智能体状态上的趋同。由于在传感网、社交网、协同控制等诸多领域具有广泛的应用背景，该问题受到越来越多研究者的关注，已成为集群智能及分布式控制研究的热点领域之一。关于多智能体一致性问题的研究可以追溯到 20世纪，一些研究者试图通过建模与仿真来发掘这些多个体系统行为背后的内在机理，Reynolds[1]对自然界中鸟群、鱼群等生物群体行为进行了颇为细致的研究，并利用计算机加以仿真，提出了著名的 Boid模型，这个模型在集群智能领域至今仍有广泛影响；Vicsek等[2]提出了基于统计力学理论的Vicsek模型，模型中分布在二维平面上的N个智能体运动速率保持不变，并根据其邻域内所有智能体的运动方向决定其自身运动方向，研究者采用离散时间一阶非线性系统来模拟群体的相位变化，该模型比较真实地模拟了自然界中的一些群集同步现象；Jadbabaie等[3]利用代数图论对Vicsek模型进行了理论解释，并对几个与Vicsek模型类似的模型的收敛性进行了理论分析，给出了Vicsek线性化模型的理论分析结果。随着研究的深入和应用范围的不断拓展，越来越多新的研究不断涌现，在理论和应用 2个层面不断推动这一领域向前发展。针对一般有向图的情形，Ren等[4]在研究中指出，在连续有界的时间隔内，若连接拓扑的并图包含有向生成树，则一致性系统渐近收敛，这个结论与后来Cao等[5]的研究结果是一致的。在对一致性问题的理论研究中，通常采用动力系统相关理论和方法作为工具，通过构造Lyapunov函数或LaSalle不变集性原理分析一致性系统收敛到一致子空间的条件，讨论了分布式一致跟踪控制问题，并将问题抽象成二阶非线性动力系统，通过对 Lyapunov函数的讨论给出了关于系统收敛性的充分条件；同样，针对跟踪控制问题，提出了分布式跟踪算法，该算法可以在有限时间内收敛至一致状态；Li等[9～13]针对多智能体一致性和复杂网络的同步问题，提出基于高阶线性系统的多智能体控制构架，并取得一系列成果；等[14]提出了采用“黑盒”代替具体动力学模型的方法，每一次迭代都采用了所谓的SOO(simultaneous optimistic optimization)方法对agent未来的动作进行规划，由于与具体的动力学模型无关，该方法能更广泛地应用于某些非线性一致性问题；关于线性一致性系统的研究，Olfati-Saber等[15～19]的工作最具影响，在其发表的一系列论文中，以图理论和动力学理论为基础，建立了一个相对完整的理论框架，并在此基础上对不同类型的一致性问题进行了系统的分析；等[20]将平均一致性问题转换成矩阵分解问题，并采用机器学习方法对矩阵分解问题进行求解；在实际应用中，通常存在agent状态与agent间传递的数据无关的情况，针对这一问题，Yu等[21～23]进行了深入的研究和讨论，提出了确保一致性协议收敛到一致状态的3个充分必要条件；针对固定拓扑网络存在可测噪声的情形，Huang等[24,25]给出了系统达到均方一致(mean square consensus)的随机近似方法；同样在固定拓扑结构下，Liu等[26]针对线性一致性协议中的噪声和信号延迟问题进行了研究，从理论上给出在non_leader_follower和leader_ follower这2种模式下，强一致(strong consensus)和均方一致的充分必要条件；Dou等[27]对线性一致性协议的噪声问题进行了研究，给出了线性一致性协议噪声可控的充分条件；在Long等[28]的研究中，agent收到的信息中含有噪声的强度与相邻 agent状态有关，在一定假设基础上，分析了固定拓扑结构、动态切换拓扑及随机切换拓扑结构下的一致性算法，并给出了确保均方一致性的充分条件；Xia等[29]从固定拓扑入手，并进一步对切变和时滞拓扑下一致性问题进行了讨论；Ren等[30]以矩阵论和控制论为工具，对非线性一致性问题进行了研究，并对给出的理论结果进行了验证；近年来这一领域的研究不断涌现，文献[31,32]对各类一致性问题进行了较为系统的综述与概括，指出了这一领域当前的主要研究成果，并分析了存在的问题及未来的发展趋势。

关于线性均方一致性噪声偏差问题的研究，通常从连续和离散时间系统出发，分别加以讨论，本文的主要贡献是：以图论和随机分析为基础，严格证明了线性离散均方一致性问题噪声偏差的上界，为线性离散一致性系统的噪声估计和控制提供了理论依据。

2 预备知识

2.1 一致性协议（consensus protocol）

本文所述的MAS可用无向图G=(V, ε)表示，其中，V={1,2,…,n}是图G的顶点集，每个顶点可视作agent的抽象，通常用序号i表示。ε∈V×V为图 G中所有边构成的集合，如果存在(i, j)∈ε，则意味着节点i和j之间存在着信息交互。对于G中节点i,用Ni={j∈V|(i, j)∈ε,j≠i} 表示与i相邻节点构成的集合，为节点i邻居的个数。

定义1节点的度（degree）：设i∈V为图G的一个节点，称与i相邻节点的个数为节点i的度，记作di，以di为对角线其他元素均为0的矩阵D=diag[d1,…,dn]称为图G的度矩阵。

定义2邻接矩阵（adjacency matrix）[15]A，称n阶矩阵A=[aij]为图G的邻接矩阵，其中，

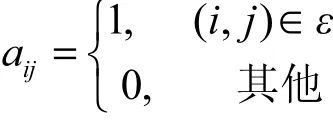
定义3Laplacian矩阵（Laplacian matrix）[15]L，称n阶矩阵L=[lij]n×n为图G的Laplacian矩阵。

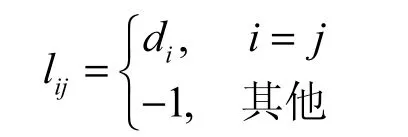
这里 A和 L均为对称矩阵，且有 L=In−A。用λ1(L)≤λ2(L)≤…≤λn( L)表示矩阵L的 n个特征值，1=[1,…,1]T为单位向量，L具有以下性质[15]。

性质1L1=0。

性质2L最小的特征值 λ1(L)=0。

性质3当且仅当G为联通图时，L的次小特征值λ2(L)＞0。

设ℝ和ℤ+分别表示实数集和非负整数集，对于∀i∈V，xi ( t)∈ℝ,t∈ℤ+为agenti在t时刻的状态，agent按某种机制进行状态的修订，若对于∀i, j∈V ，有

则称上述系统为一致性系统，agent的状态修订机制为一致性协议。通常称式(2)为离散线性一致性协议。

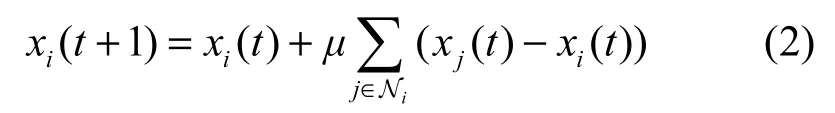
其中，µ＞0为一充分小常数，且满足µdi≤ 1。令x(k)=[x1(k),…,x(k)]T，则式(2)可写成如式(3)所示

n的矩阵形式。

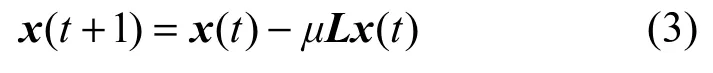
对于任意初始状态x (0)=[x1(0),…,xn(0)]T，线性一致性协议式(3)将渐进收敛至一致状态。

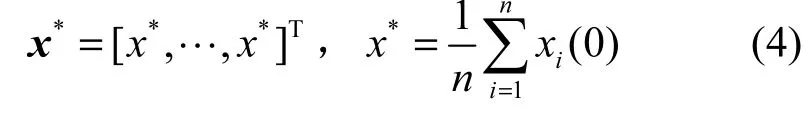
2.2 均方一致性（mean square consensus）

设r为任意满足正态分布的随机数，用mean( r)和var( r)分别表示r的均值和方差，若为一随机向量，则则为该随机向量联合分布的方差矩阵。

当agenti接收到的信息中包含着相互独立的噪声干扰时，则式(2)变为

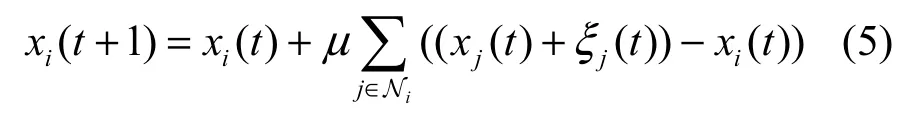
其中，ξj～N(0,1)为j所携带的噪声量，记ξ=[ξ1,…,，则var( ξ)=I，式(5)的矩阵形式为n

其中，Q=−L+ D。

定义 4均方一致[24]，在噪声条件下，对于∀i∈V ，若，且，则称一致性协议能够达成均方一致。

定义 5系统偏差[24]，称在 t时刻每个 agent状态分布方差之和为一致性系统在t时刻的系统偏差。

先前的研究[25,26]已经给出 Z(t)存在上界的充分条件，在此基础上，进一步给出Z(t)的具体上界值。

3 离散均方一致性系统的偏差上界

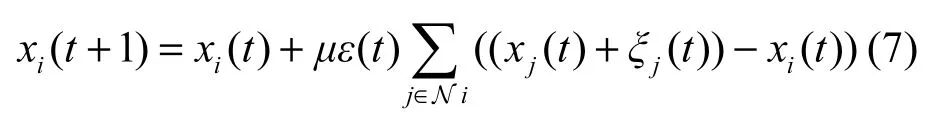
其中，ε∶ℝ+→ℝ+，被称为增益函数（gain function）。

引理1设t∈ℤ+，若函数ε( t)满足条件1和条件2，式(6)可达到均方一致。

事实上，引理1给出了一致性协议式(7)实现均方一致的充分条件，其证明过程在文献[26,27]中已有详尽的论述。

引理2设y∈ℝ为一个实数，若0≤y＜1，则式(8)成立。

证明若 0≤ y＜1，根据 e−y的泰勒展开式有

在式(9)两侧同时取对数，得

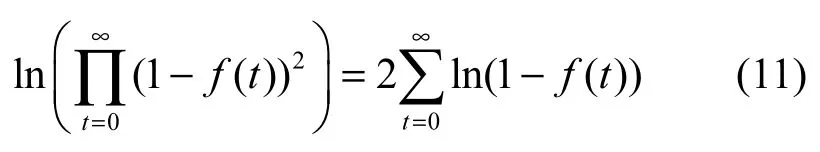
因此，式(13)成立。

在上述引理基础上，给出本文的主要结论。

定理1若G为连通图，每个节点的输出中携有标准噪声，增益函数ε满足引理1中的2个条件，且，则当t趋于无穷大时，线性离散一致性协议式(7)的系统偏差满足

其中，λ2( L)为图G相应Laplacian矩阵L最小非零特征值，h=tr(QQT)，g为与ε有关的确定常数。

证明考察式(7)的矩阵形式

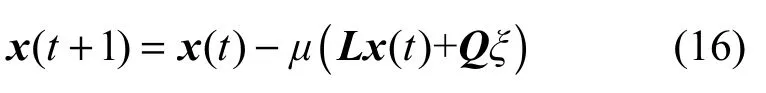
由L矩阵性质1可知，Lx*=L1x*=0，因此在式（17）右侧加一项−Lx*，等式关系不变。

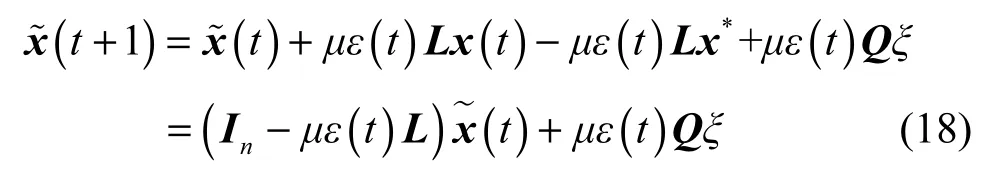
用Ft表示由生成的σ−代数，考察二阶矩的条件期望

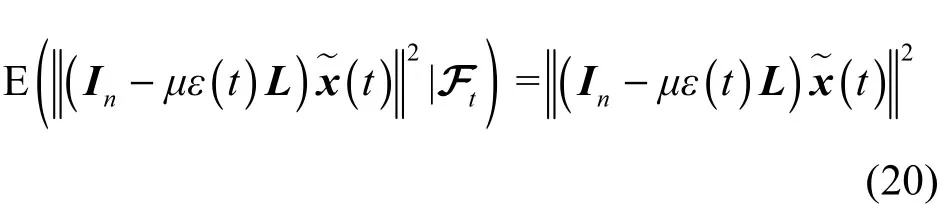
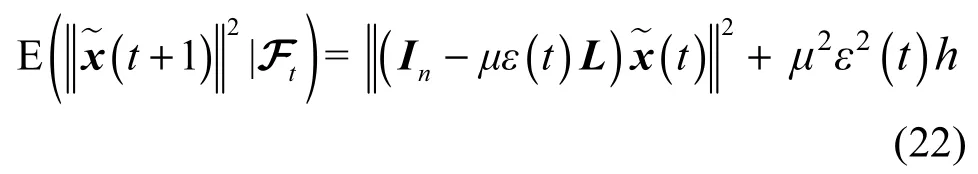
之前的研究[21]已经证明了

将式(23)代入式(22)中，从而得到式(24)。

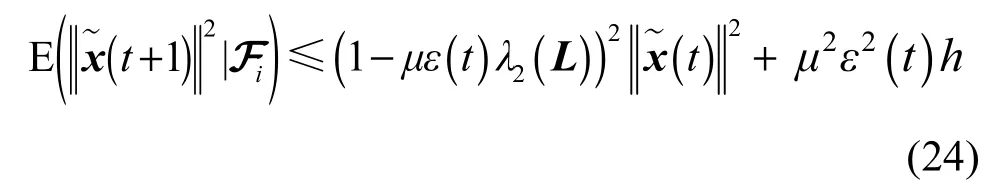
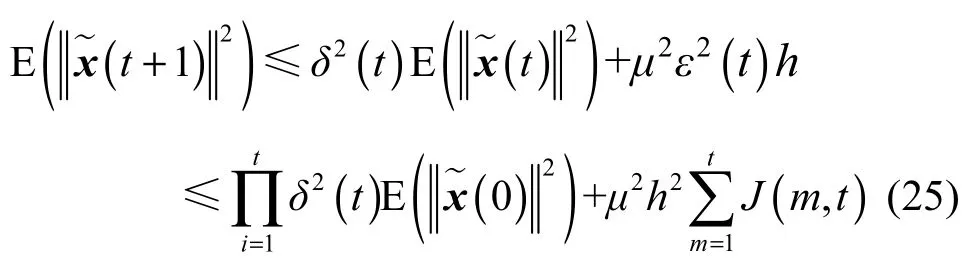
由引理 3可知：当 t趋于无穷时，式(25)右侧第一项为 0，因此，在式(25)两端同时求极限可得

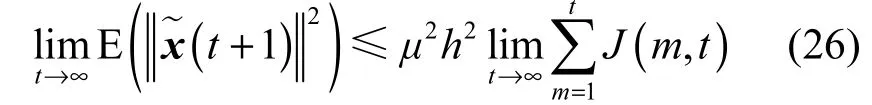
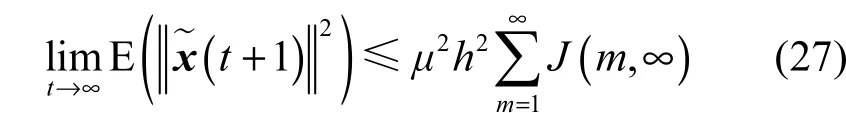
已知ε( k)满足引理1中的条件，因此必有∃k1，当k＞k1时，有

记

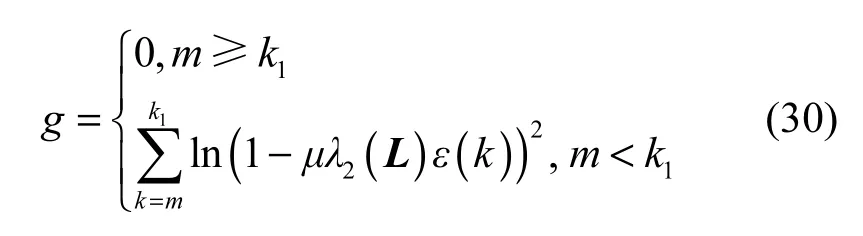
考察式(24)右侧第2项，由引理2可得

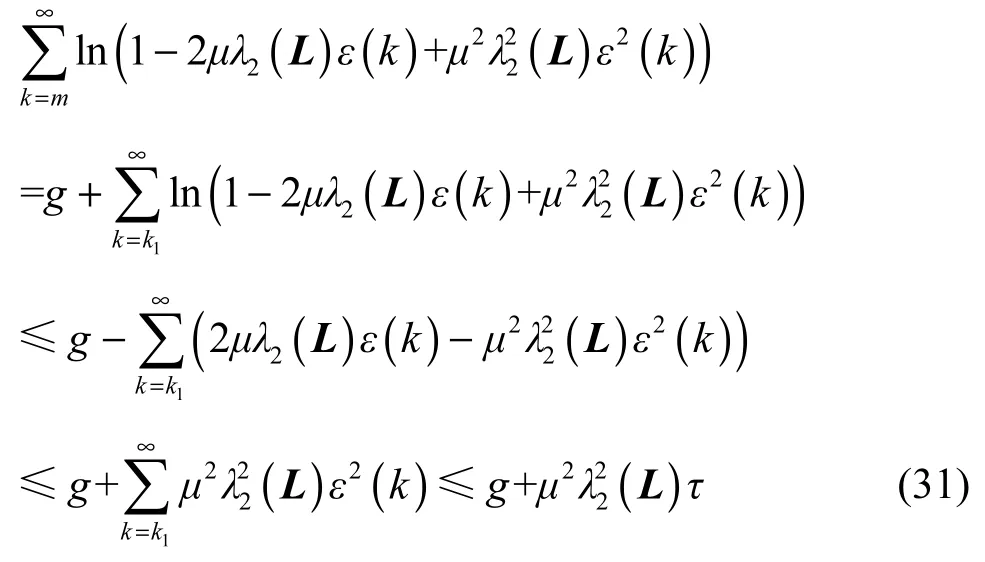
综合式(28)和式(31)，有

即

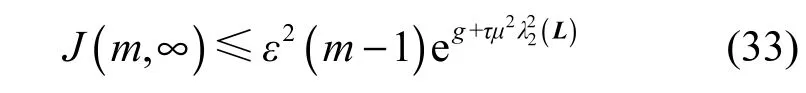
由式(33)进一步推出

综合式(26)和式(34)，即得

定理1严格地给出了线性离散均方一致性协议系统偏差 Z(t)的上界，以下通过具体示例对定理 1的使用进行说明。

4 示例

本节以星型(star)、线型(path)、环型(circle)、4-邻居环型(circle_N4)共4种不同的网络结构为例（如图1所示），对定理1的使用加以说明。

图14种agent网络结构

在图1所示的4种不同网络拓扑中，每种结构包括8个节点，即n=8，每个节点与一个agent相对应，每个agent除邻节点个数不同外，其他结构完全一致。设置参数µ=0.125，不难计算，4种结构对应的Laplacian矩阵L的次小特征值如表1所示。

表1Laplacian矩阵L的次小特征值λ2(L)

考察增益函数 ε( t)分别为(t+1)−0.6和(t+1)−1时的情形，对于∀k∉ℤ+这2种情况均有，因此g=0。当 ε( t)=(t+1)−1时，而当ε( t)=(t+1)−0.6时，求存在一定困难，可以通过式(35)求该无穷级数的一个上界

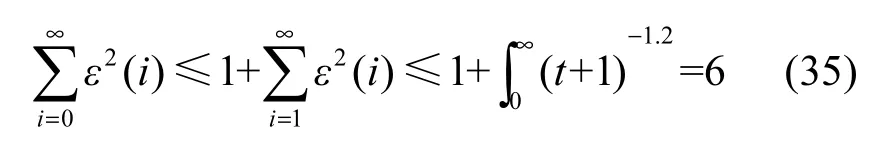
根据定理1，可以计算出以上4种结构在噪声条件下的系统偏差，具体如表2所示。

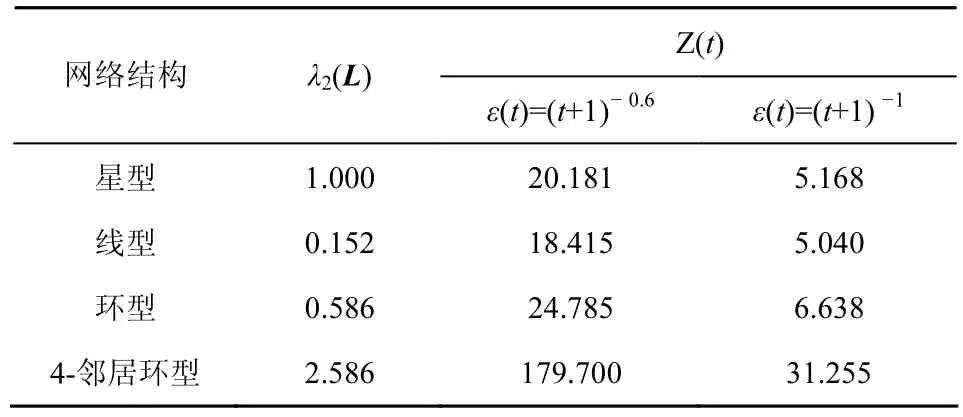
表24种网络结构系统偏差上界（当 ε(t)分别为(t+1)−0.6和(t+1) −1时）

需要说明的是，在定理1假设agent所携带噪声为标准噪声，然而在现实中这个假设通常不能满足，这种情况不难通过适当变换，将噪声变成标准噪声，因此，并不影响定理1的使用。

5 结束语

多智能体协同在传感网、社交网、协同控制等诸多领域有着广泛的应用背景，一致性问题是多智能体协同问题的核心。在现实环境中，智能体间信息的传递往往会携有噪声，一致性协议通常无法收敛至理想状态,此时噪声对系统的影响程度是本文最关心的问题。关于均方一致性方差的研究，最理想的结果是直接给出均方一致性问题方差的解析表达式，斯坦福大学和普林斯顿大学的研究者[33]做了以下尝试：首先构造关于协方差矩阵极限的李雅普诺夫方程，通过求解该方程获得协方差矩阵极限。但这些研究似乎忽略了这样一个事实，即在噪声条件下，没有引入增益函数的一致性协议的方差是不收敛的，只有引入增益函数且增益函数满足引理1的2个条件时，均方一致性问题的方差才存在极限[26,27]，然而在引入增益函数后，之前构造的李雅普诺夫方程退化成恒等方程，没有实际意义。在近期的一些研究中[26,27]，大多给出了噪声条件下，各类网络结构的线性一致系统实现均方收敛的充分条件，鲜有研究对均方一致性系统偏差做定量的估计。本文定理1给出的结论是对之前研究成果的补充。

线性均方一致性协议噪声偏差问题的研究，通常从连续和离散时间系统出发，分别加以讨论，本文的主要贡献是：对线性离散均方一致性问题进行了讨论，以图论和随机分析为基础，对线性离散一致系统的噪声偏差做了定量估计，给出了线性离散均方一致性问题噪声偏差的一个理论上界，为线性离散一致性系统的噪声分析和控制提供理论依据。

关于连续时间均方一致性问题，通常以代数图论、Itō积分及随机过程相关理论为依托，理论工具、分析方法和离散系统存在一定不同，由于篇幅所限，相应结论将在另外的研究中具体给出。

[1]REYNOLDS C W. Flocks, herds, and schools: a distributed behavioral model[C]//Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques. New York, 1987: 25-34.

[2]VICSEK T, CZIROK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical Review Letters, 1995, 75(6):1226-1229.

[3]JADBABAIE A, LIN J, MORSE A. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988-1001.

[4]REN W, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Trans Autom. Control, 2005, 50(5): 655-661.

[5]CAO M, MORSE A S, ANDERSON B D O. Reaching a consensus in a dynamically changing environment: a graphical approach[J]. Siam Journal on Control amp; Optimization, 2008, 47(2): 601-623.

[6]WEN G G, PENGA Z X, RAHMANIA A, et al. Distributed leader-following consensus for second-order multi-agent systems with nonlinear inherent dynamics[J]. International Journal of Systems Science, 2014, 45(9): 1892-1901.

[7]WEN G G, YU Y G, PENG Z X, et al. Distributed consensus tracking for second-order nonlinear multi-agent systems with a specified reference state[J]. Mathematical Problems in Engineering, 2014, 2014:320687.

[8]LU X Q, LU R Q, CHEN S H, et al. Finite-time distributed tracking control for multi-agent systems with a virtual leader[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2013, 60(2): 352-362.

[9]LI Z, DUAN Z S, CHEN G R, et al. Consensus of multi-agent systems and synchronization of complex networks: a unified viewpoint[J].IEEE Transactions on Circuits and Systems I: Regular Papers, 2010,57(1): 213-224.

[10]LI Z, DUAN Z S, CHEN G. Dynamic consensus of linear multi-agent systems[J]. Control Theory amp; Applications,2011, IET 5 (1): 19-28.

[11]LI Z, LIU X, REN W, et al. Distributed tracking control for linear multiagent systems with a leader of bounded unknown input[J]. IEEE Transactions on Automatic Control, 2013, 58(2): 518-523.

[12]WEN G, DUAN Z, LI Z, et al. Consensus and its 2-gain performance of multi-agent systems with intermittent information transmissions[J].International Journal of Control, 2012, 85(4): 384-396.

[13]WEN G, DUAN Z, LI Z, et al. Flocking of multi‐agent dynamical systems with intermittent nonlinear velocity measurements[J]. International Journal of Robust and Nonlinear Control, 2012, 22(16):1790-1805.

[14]BUSONIU L, MORARESCU I C. Consensus for agents with general dynamics using optimistic optimization[C]//Proceedings of 2013 Conference on Decision and Control (CDC-13). Florence, Italy, 2013:6735-6740.

[15]OLFATI-SABER R, FAX J A, MURRAY R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of IEEE,2007, 95(1): 215-233.

[16]OLFATI-SABER R. Evolutionary dynamics of behavior in social networks[C]//Proc of the 46th IEEE Conference on Decision and Control, 2007.

[17]OLFATI-SABER R, JALALKAMALI P. Coupled distributed estimation and control for mobile sensor networks[J]. IEEE Trans on Automatic Control, 2012, 57(9): 2609-2614.

[18]OLFATI-SABER R. Flocking for multi-agent dynamic systems: algorithms and theory[J]. IEEE Transactions on Automatic Control, 2006,51(3): 401-420.

[19]OLFATI-SABER R, FAX J A, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Trans. on Automatic Control, 2015, 49(9): 1520-1533.

[20]TRAN T M D, KIBANGOU A Y. Distributed design of finite-time average consensus protocols[C]//The 4th IFAC Workshop on Distributed Estimation and Control in Networked Systems. 2013, 4: 227-233.

[21]YU C H, NAGPAL R. A self-adaptive framework for modular robots in dynamic environment: theory and applications[J]. The International Journal of Robotics Research, 2011, 30(8): 1015-1036.

[22]YU C H. Biologically-inspired control for self-adaptive multiagent systems[D]. MA Cambridge: Harvard University, 2010.

[23]YU C H, NAGPAL R. Biologically-inspired control for multi-agent self-adaptive tasks[C]//Proc of the 24th AAAI Conference on Artifical Intelligence. 2010: 1702-1709.

[24]HUANG M, MANTON J H. Coordination and consensus of networked agents with noisy measurements: stochastic algorithms and asymptotic behavior[J]. SIAM Journal on Control and Optimization,2009, 48(1): 134-161.

[25]HUANG M, MANTON J H. Stochastic consensus seeking with noisy and directed inter-agent communication: fixed and randomly varying topologies[J]. Institute of Electrical and Electronics Engineers, Transactions on Automatic Control, 2010, 55(1): 235-241.

[26]LIU S, XIE L, ZHANG H. Distributed consensus for multi-agent systems with delays and noises in transmission channels[J]. Automatica, 2011, 47(5): 920-934.

[27]DOU Q S, CHONG L, JIANG P. Research on discrete linear consensus algorithm with noises[J]. Acta Automatica Sinica, 2015, 41(7):1328-1340.

[28]LONG Y, LIU S, XIE L. Distributed consensus of discrete-time multi-agent systems with multiplicative noises[J]. International Journal of Robust and Nonlinear Control, 2015, 25(16): 3113-3131.

[29]XIA H, HUANG T Z, SHAO J L, et al. Group consensus of multi-agent systems with communication delays[J]. Neuro Computing,2016, 171 (C): 1666-1673.

[30]REN T, WANG Y F, LIU MM, et al. The consensus of nonlinear multi-agent system with switching topologies and communication failure[J]. Journal of Intelligent and Fuzzy Systems, 2016, 30(2): 1199-1206.

[31]GARIN F, SCHENATO L. Distributed estimation and control applications using linear consensus algorithms[EB/OL]. http: //citeseerx.ist.psu.edu /viewdoc/summary?doi=10.1.1.382.9187.

[32]MIN H B, LIU Y, WANG S C, et al. An overview on coordination control problem of multi-agent system[J]. Acta Automatica Sinica,2012, 38(10): 1557-1570.

[33]YOUNG G F, SCARDOVI L, LEONARD N E. Robustness of noisy consensus dynamics with directed communication[C]//American Control Conference. 2010: 6312-6317.

Upper bound of mean-square deviation of discrete linear consensus system

DOU Quan-sheng1,2, LI Yu-rong1, JIANG Ping1
(1. School of Computer Science and Technology, Shandong Institute of Business and Technology, Yantai 264005, China;2. Shandong Vehicle Networking Engineering Technology Research Center, Yantai 264005, China)

The consistency problem is the basis of cooperative control of multi-agents, and has wide application background. The previous research has given the sufficient condition for the linear consistency protocol to realize mean-square consistency problem . Based on graph theory and random analysis, the noise-deviation upper bound of linear discrete mean-square consistency problem was strictly proved further, at the same time, four different network were used as examples to explain the theoretical results. The conclusion provides theoretical basis for the noise evaluation and control of the linear discrete consistency system.

collective intelligence, multi-agent system, consensus protocol, noisy problem, mean square consensus

s:The National Natural Science Foundation of China (No.61272244, No. 61672327, No.71471103), The National Basic Research Program of China (973 Program) (No. 2013CB329502), The Natural Science Foundation of Shandong Province(No.ZR2014FL007)

TP301.6

10.11959/j.issn.1000-436x.2016193

2016-05-12；

2016-08-21

国家自然科学基金资助项目（No.61272244, No.61672327, No.71471103）；国家重点基础研究发展计划（“973”计划）基金资助项目（No.2013CB329502）；山东省自然科学基金资助项目（No.ZR2014FL007）