高效的可撤销群签名方案

2016-11-24仲红黄丛林许艳崔杰

通信学报 2016年10期

关键词：私钥子集差分

仲红，黄丛林，许艳，崔杰

（安徽大学计算机科学与技术学院，安徽合肥 230601）

高效的可撤销群签名方案

仲红，黄丛林，许艳，崔杰

（安徽大学计算机科学与技术学院，安徽合肥 230601）

将子集覆盖框架与Camenisch-Stadler方案相结合，实现群成员的加入和撤销，且无需改变其他成员私钥，实现高效的签名验证效率。同时，在成员注册时增加一个知识签名，实现防联合攻击。分析表明，方案满足匿名性和抗联合攻击、伪造攻击和权威陷害攻击，并具有非关联性。效率方面，仅略增加群成员证书长度，达到常数级的签名和验证开销。

群签名；子集覆盖框架；联合攻击；非关联性

1 引言

群签名（group signature）概念是1991年由Chaum和Heyst首次提出[1]的，在群签名中，群成员可以匿名代表群进行签名，验证者只能验证签名是否由群成员签署，却不能确定签名者的身份。必要时，如签名被举报，群管理员可以打开签名追踪签名者真实身份。由于这些特征，群签名能广泛运用于政务、商务等场景[2～4]。早期提出的群签名方案中，群公钥或签名长度与群成员数线性相关，签名效率低，不适合大群。1997年，Camenisch等[5]首次提出适用于大群的群签名方案，该方案中的群签名长度和群公钥是固定的，独立于群成员个数，且加入新成员时无需改变其他成员私钥，但该方案不能撤销群成员。

然而，在实际应用中，群中成员是动态加入和退出的，其中，成员撤销是群管理员主动撤销非法群成员或群成员主动离开群。例如，某恶意群成员发送的非法信息遭举报，群管理员核实后将该恶意成员踢出群，保障群中其他合法成员安全。2003年，王尚平等[6]在Camenisch-Stadler群签名方案基础上，提出利用更新算子进行成员撤销的解决方案，当群成员加入或撤销时，群管理员公布群特性公钥和成员特性私钥更新算子，群成员根据更新算子计算签名密钥，但不能完全撤销群成员。Libert等在2005年[7]和Nakanishi[8]在2009年都提出离线验证的群成员撤销方案，群成员维护一个撤销列表，撤销信息仅发送给验证者进行验证，签名开销独立于撤销群成员数量，但每次撤销群成员都要更新撤销列表，验证开销与撤销成员数呈线性增加。2008年，李新社等[9]对文献[6]方案进行改进，群成员计算自己的特性密钥，然后交给群管理员计算特性密钥更新算子，实现群成员有效撤销。群成员每次加入或撤销时，群管理员都要重新计算自己的特性公钥和群成员的特性密钥更新算子，大大增加群管理员计算开销。2011年，Fan等[10]提出基于累加器的群签名撤销方案，群管理员负责更新撤销信息，然而，群成员撤销时，群管理员需要更新每个群成员的签名密钥，大大增加了群管理员的计算量。2012年，Libert等[11]提出个可扩展撤销方案，实现群成员加入或撤销时，签名和验证复杂度独立于群成员数量，但群成员需要存储O(log3N)的成员证书，大大增加系统的存储代价。2014年，张德栋等[12]针对Camenisch-Stadler方案提出一个有效成员撤销解决方案，利用群成员证明其身份不在排序的撤销列表中，达到撤销目的，但该方案在签名证明和验证签名时使用较多的模幂运算，效率较低。近年，一些新型群签名也被提出，如基于格群签名[13]、基于量子群签名[14]等。

本文将子集覆盖框架中的完备子树方法和子集差分方法分别与Camenisch-Stadler方案相结合，提出2种可撤销的群签名方案。子集覆盖框架原本是针对广播加密的密钥分发提出的，群管理员将群成员对应一个完备树的叶节点，同时为树中每个节点分配一个密钥值，将群成员对应叶节点到根节点的值发送给对应群成员，作为签名密钥；然后，群管理员选取包含群中所有合法节点的子集，公布子集节点对应密钥值，这样，合法群成员就利用自己存储的与群管理员公布相同的密钥值进行签名，被撤销成员无法找到对应值进行签名，达到撤销成员目的。同时，通过在成员向群管理员注册时增加一个知识签名，弥补Camenisch-Stadler方案不能抗联合攻击问题，防止成员联合进行内联注册，进而伪造签名。最后，对本方案安全性和效率进行分析，得出方案具有如下优点：1) 当有群成员加入和撤销时，无需改变其他群成员的签名私钥和证书；2)群签名长度和验证开销独立于群成员数和撤销成员数。

2 预备知识

2.1 子集覆盖框架

子集覆盖框架是由Naor等[15]提出，用于广播加密密钥分发。根据选取子集的方法不同，分为完备子树方法和子集差分方法。

2.1.1 完备子树方法

完备子树方法中，首先构建一个l=logN−1层的完全二叉树T，树中节点标记为xi,j，i∈l, j∈N ，把用户分配到叶节点xl,j，用户存储其对应叶节点到根节点路径上所有节点值。N是叶节点总数，R是被撤销叶节点。完备子树方法选取包含所有未被撤销合法叶节点的m个子树集合S1, S2,···,Sm，

如图1所示，高为3的完全二叉树有8个叶节点，对应8个用户，其中，x3,1、x3,7、x3,8是要撤销的节点。利用完备子树方法选取包含未撤销叶节点的子集为Si={x3,2,x2,2,x2,3}，其中，i=3。

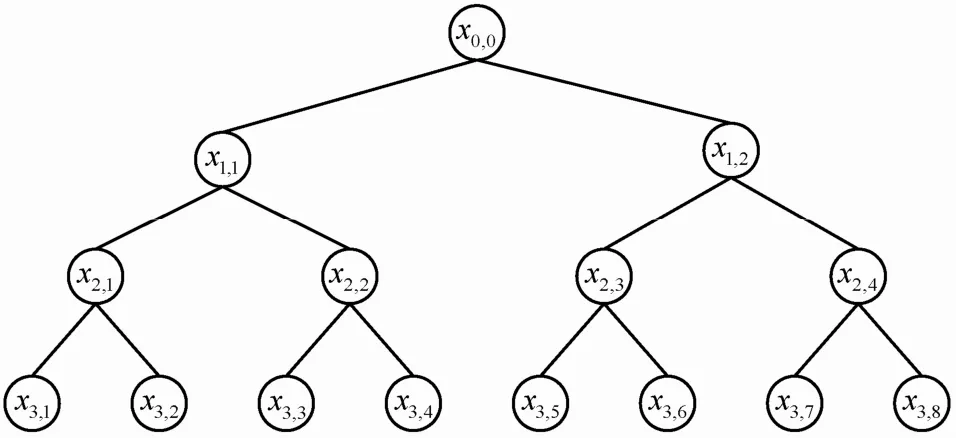
图1完备子树方法示例

2.1.2 子集差分方法

同完备子树方法，首先构建一个l=logN−1层的完全二叉树T，树中节点标记为xi,j，i∈l, j∈N ，把用户分配到叶节点xl,j。集合S表示在以xi,j为根节点的子集中且不在以xp,q为根节点的子集中的节点集合，其中，xi,j是xp,q根节点。子集差表示为S=xi,j−xp,q，为每个S选取不同的值，令wj为从叶节点xl,j到根节点x0,0路径上所有节点的兄弟节点（根节点无兄弟节点）。用户存储从其对应叶节点xl,j到根节点路径上的所有节点xi,j减去以其为根的xl,j所有兄弟节点wj的集合Sj值，其中，j=l2。子集差分方法利用差集选取包含所有未撤销叶节点成员的子集Sm，m≤2R−1。

如图2所示，高为3的完全二叉树有8个叶节点，对应8个用户，其中，x3,1、x3,7、x3,8是要撤销的节点。利用子集差分方法选取包含未撤销叶节点的子集为Si={(x2,1−x3,1),(x1,1−x2,1),(x1,2−x2,4)}，其中，i=3。

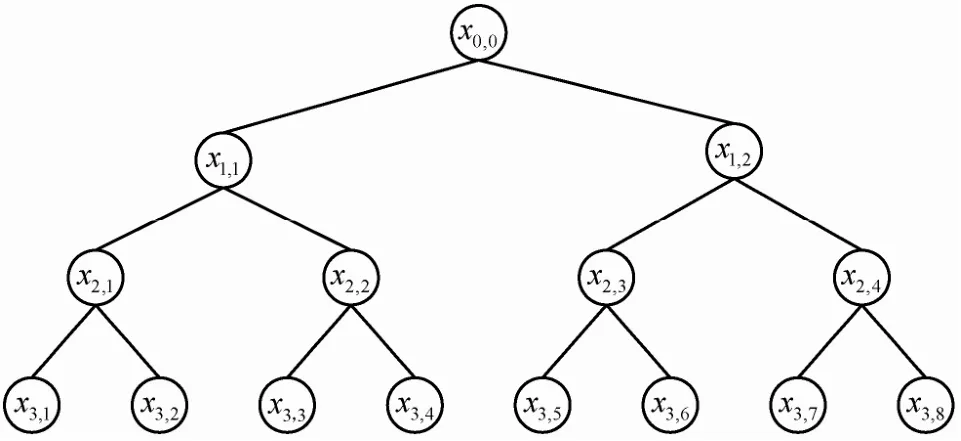
图2子集差分方法示例

2.2 基于离散对数的知识签名

知识签名是一种数学构造，签名者可以利用这种数学构造在不泄露某秘密的前提下，证明自己拥有这个秘密。本方案使用基于离散对数的知识签名，具体如下。

称使等式c=H( g||y||gsyc||m)成立的二元组(c, s)∈{0,1}k×Z*n为对消息m关于y∈G的离散对数知识签名，表示为SKLOG{α∶y=ga}。其中，H∶{0,1}*→{0,1}k是具有抗碰撞性的散列函数。假设成员拥有使等式y=gx成立的私钥x，对消息m的知识签名(c, s)获得步骤如下。

2) 计算c=H( g||y|| t||m)。

3) 计算s=(r−xc)modn。

3 本文方案

3.1 系统初始化

1) 群管理员身份为IDC，选取一个RSA模数nC和一个散列函数h(·)。选择公开指数e1, e2＞1和正整数f1,f2＞1，且e2与φ(nC)互素，nC因式分解未知，f1,f2的e1次根和e2次根是计算困难的。

2) 选择在其中计算是离散对数困难的循环群G=＜g＞，阶为nC，元素h∈G是以g为基的离散对数，是计算困难的。

3) 选择私钥xC∈Zn*，令yC=hxC(modnC)。随机选择eC∈Z*n，计算dC满足eCdC≡1(modφ(nC))。其中，yC、eC为群管理员公钥，xC、dC为群管理员私钥。公开(nC,yC,e1, e2,f1,f2, G, g, h)。

4) 群管理员建立一个层数为l=logN−1的完全二叉树T，N为树中叶节点数。树中节点被标识为xi,j，i=0,···,l和j=0,···,2i分别表示每层和对应层的节点。群管理员为每个群成员Uj分配树中叶节点xl,j。利用以下完备子树方法或子集差分方法初始化。

①完备子树方法。对每个节点xi,j，群管理员选择一个对应整数bk，bk也相当于以对应节点为根的子集Sj值，其中，k=0,···,2l−1。使ak满足akbk≡1(modφ(nC))，最终群管理员存储每个树节点元组(xi, j,gak,bk,(bk)dC)。此过程在群管理员后台离线运行，并不占用签名时间。将从树根节点到用户对应叶节点路径上所有节点元组发送给Uj。群管理员存储每个用户信息元组表

②子集差分方法。对每个叶节点xl,j，群管理员选取xl,j到根节点路径上的所有节点xi,j减去以xi,j为根到xl,j路径上所有兄弟节点wj的集合Sj，为每个集合Sj选取一个对应整数bk，其中，k=0,···,2l2−1。使ak满足akbk≡1(modφ(nC))。发送对应元组{gak,b,(b)dC}l2给U。群管理员存储kkk=0j每个用户信息元组表(ID, x,{gak,b,(b)dC}l2)。jl, jkkk=0

5) 假设系统中有n个成员(n≥2)。群管理员利用完备子树方法或子集差分方法，选取包含所有未撤销用户对应叶节点的子树集合Sm，用每个子树的根节点表示对应子集，m为子集数目。如图1和图2所示，群管理员公布子集Sm对应的bk集合，其中，t为时间戳。

3.2 成员加入

1) 用户Ui要加入群，首先随机选择xi∈，令yi=xe1i(modnC)，计算身份IiD=gyi(modnC)，

其中，xi、yi是其身份私钥，并产生一个IDi对g的知识签名[16]W=SPK[λ∶IDi=gλ](′)。

2) 为防止申请成员证书时群管理员伪造签名，Ui计算yi的盲化值yi*

以及IDi和的知识证明为

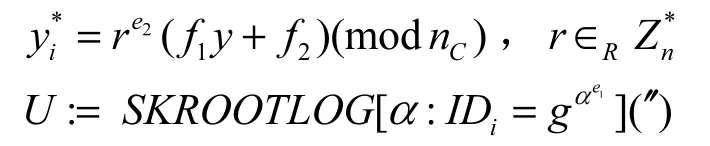
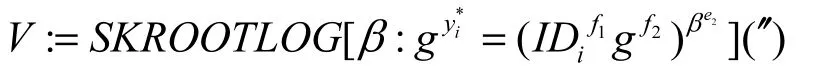
Ui将IDi、yi*、W、U、V发送给群管理员。

3) 群管理员验证W、U、V是否正确，若正确，则确信yi*是IDi所含成员密钥的盲化值，并计算。然后群管理员根据子集覆盖给Ui分配一个T中叶节点xl,i，群管理员用完备子树方法选择从叶节点xl,i到根节点路径上所有节点元组或利用子集差分方法选取从其对应叶节点xl,j到根节点路径上的所有节点xi,j减去以其为根的xl,j所有兄弟节点wj的集合Sj值，并存储用户元组表。将Ui部分证书发送给Ui。4) U收到H后，验证v*=((v*)dC)eC，若等式iii成立，则确认是群管理员发送并保存，计算最终成员证书为

5) 群管理员利用子集覆盖框架方法，重新选取包含新加入成员和其他所有合法用户对应叶节点的子树集合Sm，并公布其对应bk集合C=(t,{ bk}mk=1)。

3.3 成员撤销

群管理员若要撤销成员Uj，利用完备子树方法，首先定位到Uj对应叶节点xl,j，重新选择不包含Uj对应叶节点的子集。根据树形结构可知，完备子树方法中只需避免选择从xi,j到根节点路径上节点即可，其他子集节点不变，最后，发布新的子集列表Sm'={xi,j}i∈l,j∈2i所对应bk集合C=(t,{ bk}mk=1)；子集差分方法只需选取新的不包含Uj对应叶节点的差集S=xi,j−xp,q的bk值即可，最后也发布新的子集列表对应集合C。由于新子集列表不包含Uj存储的bk，Uj无法利用其产生合法签名。

3.4 签名

1) Ui要对消息m进行签名，首先根据群管理员最新发布的C和自己的成员证书{gak,b,(b)dC}l找kkk=0到相同b，然后利用(gat,b)元组进行签名。其中定tt能找到唯一相同bt，因为群管理员根据子集覆盖框架中方法选取包含Ui对应叶节点的子集时，必会选取Ui存储的从xl,i到根节点路径上一节点或子集差中包含其叶节点（此步骤可在签名前离线处理，只要收到新的C即可）。然后计算q=(gat)h(m)(modnC)。

2) 与原方案相同，Ui首先计算对信息的知识签名，证明是其群成员；其次，利用群管理员的公钥对其成员公钥进行加密，让群管理员在必要时可以打开签名。具体描述如下。

3.5 验证

Uj收到Ui的签名，首先确认bt在最新群公布列表中，验证等式b=((b)dC)eC(modn)和gh(m)=ttC qbt(modn)是否成立，若都成立，验证消息的完整C性和Ui是未被撤销成员群成员，否则拒绝签名。然后验证(V1, V2, V3)的正确性，若正确，验证者确信δe2=fβe1+f(modn)，γ=αf(modn)，从而使12C1C验证者相信IDi*和d的计算使用了同一个随机数r=ε，接受签名。同时确保在必要时，群管理员可以打开签名。

3.6 追踪

本方案的追踪过程与原群签名方案的追踪过程完全一致，通过计算来追踪Ui身份。

4 安全性和效率分析

本节对方案的安全性和效率进行分析。安全性主要包括正确性、匿名性、防联合攻击、防伪造攻击、防权威陷害攻击、非关联性6个方面内容。此外，将方案安全性和效率与已有方案进行对比，体现本方案的优势。

4.1 安全性分析

4.1.1 正确性

1) 验证者首先通过检查bt是否在最新群公布的列表C中来判断签名者是否被撤销；通过验证等式和来确认签名的合法性和消息完整性。因为中dC是群管理员私钥，表明bt是群管理员私钥签署；因为，其中，h( m)表明消息的完整性，gat是成员注册时群管理员秘密发送给群成员的，等式成立表明该成员是合法群成员。

3)若群管理员追踪签名者Ui身份，发现其有非法行为，就要把Ui撤销。根据子集覆盖中完备子树方法或子集差分方法，群管理员选取新的子集时不包含Ui存储的元组对应节点，然后发布新子集节点对应的bk集合。这样，Ui在签名时无法在新C中找到相同bk，无法通过等式验证，因为解为离散对数困难性问题。因此，Ui被撤销。

4.1.2 匿名性

Ui签名为，其中，是Ui身份IDi的盲化值，每次签名都取不同随机数进行盲化，攻击者若想从IDi*中计算得出IDi，就要解决离散对数困难性问题。因此，本方案满足匿名性。

4.1.3 防联合攻击

1)若n＞1个群成员想联合进行共模攻击[16]，则需得到nC分解因子，从而攻破群系统，伪造其他任何成员签名。但通过进行共模攻击分解nC，就要知道ak和bk。由于群成员只知道和，求解ak等价于求解离散对数困难问题。因此，群成员无法进行联合攻击分解nC。

2)根据周玉等[17]对 Camenisch-Stadler方案安全分析可知，在不知nC因式分解前提下，群成员可以联合攻击，以此伪造密钥身份证书进行签名，并被跟踪。此类攻击策略是几个用户利用关联的私钥注册，获得内在关联的身份证书，然后算出群管理员签名的关键因子。本方案在用户注册时产生一个对g的知识签名，防止用户关联私钥进行注册。同时，在签名验证时验证的正确性，使验证者确信，从而验证者相信和d的计算使用同一个随机数r=ε，即是Ui利用群管理员公钥(h, yC)对成员公钥IDi的一个ElGamal加密。若群中能够产生有效、不被追踪的签名，则表明群成员能伪造群私钥，其难度相当于求解离散对数困难性难题。

4.1.4 防伪造攻击

若成员 Uj想要伪造一个可通过验证的签名，且真实身份不被追踪。Uj可从以下3个方面进行伪造攻击。

1)Uj联合其他成员利用关联注册或共模攻击分解nC，从而攻破整个系统，进行伪造攻击。由4.1.1节可知，本方案在注册时利用知识签名实现防联合攻击，Uj无论被撤销与否，都不能联合攻击，也无法利用共模攻击分解nC，从而不能伪造签名。

2) Uj从收到的签名中获取签名信息伪造签名。假设Uj收到成员Ui的签名σi，利用其(q, bt,签名信息伪造签名。若Uj被撤销，群管理员利用子集覆盖中方法选择的子集对应值并不在Uj存储的元组列表中，解gat为离散对数困难性问题，因此，Uj签名无法通过Ui等式验证；若未被撤销，在群管理员公布的I中找到自己存储Ui对应元组IDi，签名能够通过I等式验证，但由于不知IDi私钥和分解，无法通过正确性验证。因此，Uj无法成功利用其他成员签名信息伪造签名。

3)Uj被撤销后，修改自己的签名和验证，信息通过验证来伪造签名。由于Uj被撤销，C被更新，其存储的bk不属于当前群发布C中的值，已不能通过验证。Uj想伪造bt′和q′值进行签名，并通过验证，但U无法获知群j私钥dC，无法通过验证。所以，无法通过修改信息伪造签名。

4.1.5 防权威陷害攻击

本文方案中成员Ui向群管理员注册时，Ui只将yi的盲化值和IDi发送给群管理员，其私钥信息xi,yi并未告知群管理员，群管理员若要伪造Ui签名，计算中y为离散对数难题。i所以，群管理员无法冒充群成员进行签名。

4.1.6非关联性

根据树结构特性，本方案中bk并不是唯一对应一个成员身份，即使群成员收到签名中的bk，也无法确定bk对应多少成员身份，更无法定位到哪个成员，满足非关联性。

4.2 效率分析

针对效率分析，本方案对基于完备子树方法方案和基于子集差分方法方案效率都进行了分析和对比。对比方案都满足成员撤销，如表1所示，既有基于双线性对的Libert方案[7]和Nakanish方案[8]，又有对Camenisch-Stadler方案修改的李新社方案[9]和张德栋方案[12]。同时给出了本文方案与李新社方案[9]和张德栋方案[12]的详细开销对比，体现了本文方案具有一定优势。表1中，“T”表示撤销成员次数，“R”和“N”分别表示撤销成员数和成员总数；表2中，“E”表示模幂运算次数，“H”表示散列运算次数。

从表1可知，本文完备子树方案和子集差分方案在群公钥长度、签名长度以及签名开销和验证开销都是最低的O(1)，完备子树方案增加了少量撤销开销，但达到比子集差分方案更小的成员证书长度；子集差分在撤销开销和存储方面更低，但增加了成员证书存储。相比其他方案，本文 2种方案在群公钥长度、签名长度、签名开销和验证开销复杂度都是最低，其中，完备子树的撤销列表长度也较低；虽然张德栋方案撤销开销更低，但其签名、验证具体开销大大高于本文 2种方案，且本文撤销开销都是查询逻辑树结构代价，并非计算代价。综合对比，本文方案具有更平衡的整体开销。

表1各协议开销复杂度对比

表 2开销详细对比中的方案都是基于对Camenisch-Stadler方案的修改方案，从对比中可知，本文2种方案的签名开销最低，验证开销略高于李新社方案，但李新社方案撤销计算开销太大，撤销开销只比张德栋方案略高，但张方案在签名和验证开销使用了大量的散列函数和指数运算，开销明显高于本文方案；同时，本文撤销开销为群管理员选取子集时查询代价，无需大量计算开销。故在整体开销方面，本方案是对比方案中最好的。

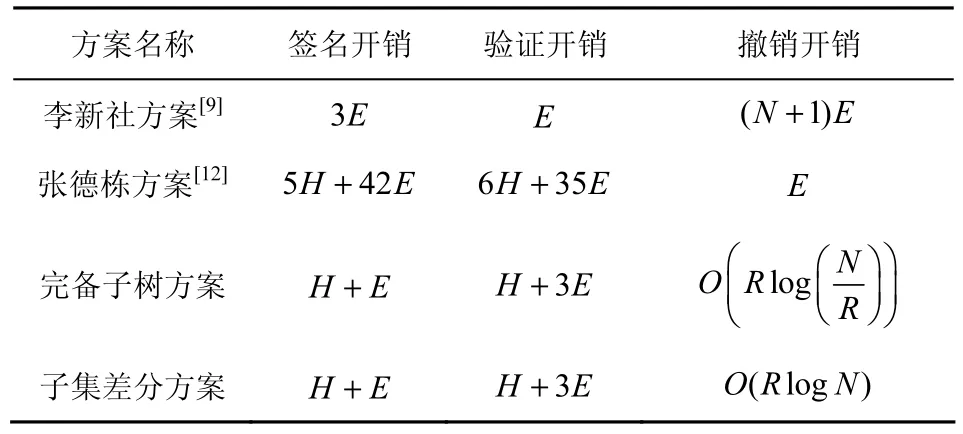
表2开销详细对比

5 结束语

本文方案通过将子集覆盖框架的完备子树方法或子集差分方法与Camenisch-Stadler方案相结合，实现了成员撤销和加入，并在成员注册时增加一次知识签名，实现了防联合攻击，同时，还实现了匿名性、防伪造性和防权威陷害攻击以及非关联性。效率方面，通过对本文2种方法方案对比可见，完备子树方案适合群管理员计算能力和开销较强，用户只需存储很少成员证书的情况；而子集差分方法适合群管理员计算和存储能力适中，用户存储能力较强的情况。在与其他方案对比中可看出，本方案具有更平衡的整体开销，体现了本方案的一定优势。但本文2种方案在撤销时的查询代价与撤销成员数相关，如何减少撤销代价有待今后进一步研究。

[1]CHAUM D, VAN H E. Group signatures[M]//Advances in Cryptology.Berlin Heidelberg: Springer, 1991: 257-265

[2]MALINA L, VIVES-GUASCH A, CASTELLÀ-ROCA J, et al. Efficient group signatures for privacy-preserving vehicular networks[J].Telecommunication Systems, 2015, 58(4): 293-311.

[3]KUZHALVAIMOZHI S, RAO G R. Privacy protection in cloud using identity based group signature[C]//2014 Fifth Applications of Digital Information and Web Technologies (ICADIWT), IEEE. 2014: 75-80.

[4]MALINA L, SMRZ J, HAJNY J, et al. Secure electronic voting based on group signatures[C]// 201538th International Conference on Telecommunications and Signal Processing. 2015: 6-10.

[5]CAMENISCH J, STADLER M. Efficient group signature schemes for large groups[M]//Advances in Cryptology. Berlin Heidelberg: Springer,1997: 410-424.

[6]王尚平, 王育民, 王晓峰, 等. 群签名中成员删除问题的更新算子解决方案[J]. 软件学报, 2003, 14(11): 1911-1917.WANG S P, WANG Y M, WANG X F, et al. A new solution scheme for the member deletion problem in group signature by use of renew operator[J]. Journal of Software, 2003, 14(11): 1911-1917.

[7]LIBERT B, VERGNAUD D. Group signatures with verifier-local revocation and backward unlinkability in the standard model[M]//Cryptology and Network Security. Berlin Heidelberg: Springer, 2009:498-517.

[8]NAKANISHI T, FUNABIKI N. Verifier-local revocation group signature schemes with backward unlinkability from bilinear maps[M]//Advances in Cryptology. Berlin Heidelberg: Springer, 2005: 533-548.

[9]李新社, 胡予濮. 一个群签名成员删除方案的分析和改进[J]. 西安电子科技大学学报, 2008, 35(3): 478-482.LI X S, HU Y P. Analysis and improvement of the group signature member deletion scheme[J]. Journal of Xindian University, 2008,35(3): 478-482.

[10]FAN C I, HSU R H, MANULIS M. Group signature with constant revocation costs for signers and verifiers[M]//Cryptology and Network Security. Berlin Heidelberg: Springer, 2011: 214-233.

[11]LIBERT B, PETERS T, YUNG M. Scalable group signatures with revocation[M]//Advances in Cryptology. Berlin Heidelberg: Springer,2012: 609-627.

[12]张德栋, 马兆丰, 杨义先, 等. 群签名中成员撤销问题解决方案[J].通信学报, 2014, 35(3): 193-200.ZHANG D D, MA Z F, YANG Y X, et al. New solution scheme for the member revocation in group signature[J]. Journal on Communications,2014, 35(3): 193-200.

[13]LING S, NGUYEN K, WANG H. Group signatures from lattices:simpler, tighter, shorter, ring-based[M]//Public-Key Cryptography.Berlin Heidelberg: Springer, 2015: 427-449.

[14]SU Q, LI W M. Improved group signature scheme based on quantum teleportation[J]. International Journal of Theoretical Physics, 2014,53(4): 1208-1216.

[15]NAOR D, NAOR M, LOTSPIECH J. Revocation and tracing schemes for stateless receivers[M]//Advances in Cryptology. Berlin Heidelberg:Springer, 2001: 41-62.

[16]STINSON D R. Cryptography: theory and practice[M]. CRC Press, 2005.

[17]周玉, 施荣华, 胥磊. Camenisch—Stadler 群签名方案安全性的进一步分析与改进[J]. 计算机工程与应用, 2007, 42(35): 130-132.ZHOU Y, SHI R H, XU L. Further analysis and improvement for Camenisch-Stadler group signature schemes[J]. Computer Engineering and Applications, 2007, 42(35): 130-132.

Efficient group signature scheme with revocation

ZHONG Hong, HUANG Cong-lin, XU Yan, CUI Jie
(School of Computer Science and Technology, Anhui University, Hefei 230601, China)

A group signature scheme which combines the subset cover framework with Camenisch-Stadler scheme was proposed. This scheme allowed any group members’ entrance and revocation without changing other members’ secret key.Meanwhile, the scheme added a knowledge signature while registering, that realized coalition resistance. It is shown that the scheme not only has the characteristics of anonymity and no-relation, but also can resist conspiracy attacks, forgery attack and authority trap attack. As for efficiency, the scheme just slightly increases the length of group members’ certificates, with the signature and verification complexity remaining at constant level.

group signature, subset cover framework, conspiracy attack, no-relation

s:The National Natural Science Foundation of China (No.61572001), The Natural Science Foundation of Anhui Province (No.201508085QF132)

TP309.7

10.11959/j.issn.1000-436x.2016191

2016-02-02；

2016-06-07

黄丛林，hcllin313@163.com

国家自然科学基金资助项目（No.61572001）；安徽省自然科学基金资助项目（No.201508085QF132）