合并单元常用加窗处理算法抗电磁干扰能力分析
2016-11-24兰春虎王兆峰
范 巍 兰春虎 王兆峰 王 江
(1国网天津市电力公司电力科学研究院天津3003842国网天津市电力公司经济技术研究院天津300171 3国网天津市电力公司天津300010)
合并单元常用加窗处理算法抗电磁干扰能力分析
范巍1兰春虎2王兆峰2王江3
(1国网天津市电力公司电力科学研究院天津3003842国网天津市电力公司经济技术研究院天津300171 3国网天津市电力公司天津300010)
设计了一种基于LabVIEW的电子式电流互感器校验仪,详细分析了三角自卷积窗算法的实现流程。模拟合并单元各类常用的数据处理算法,并在不同信噪比条件下,进行基波参数提取试验,对测试数据进行了误差分析。实验结果显示,在取消电子式电流互感器出口端二次转换模块的条件下,合并单元可以通过软件算法消除电磁干扰的影响,提供误差范围符合规范要求的数据。
合并单元;电子式电流互感器;校验仪;三角自卷积窗;误差分析
1 引言
2009年5月国家电网公司提出了建设坚强智能电网的目标,智能变电站是实现目标的重要环节。而电子式互感器又是智能变电站核心技术之一,是智能变电站信息化、数字化、自动化、互动化的基础,解决了传统互感器体积大、成本高、暂态性能差的难题。但是随着一次设备向小型紧凑化方向发展,留给互感器的空间越来越小。为节约空间,二次厂家倾向于取消互感器出口的二次变换器,将其移至合并单元内部,使互感器输出的模拟信号通过电缆直接进入合并单元。在没有试验验证该做法可行的情况下,设备接收方担心由于暴露在电磁干扰环境中的二次电缆较长,导致信号中噪声大,进而使合并单元输出数据的误差超过规范要求范围,影响互感器的数据可信度。
2 采用傅里叶变换的误差计算
根据GB/T20840.8-2007中电子式互感器的误差定义,分析电子式电流互感器的幅值误差及相位误差计算方法如下:
ip(tn)和is(n)皆为周期性信号。这些信号数字化后的离散傅里叶变换如下所示:
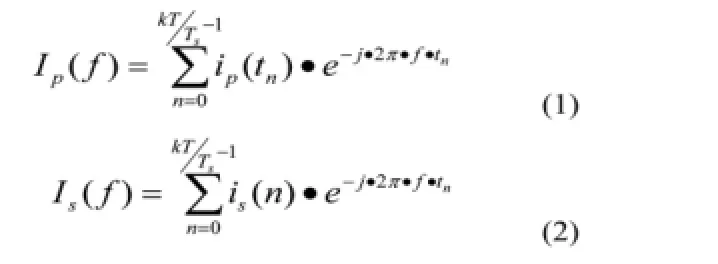
式中,ip为一次电流幅值,is为被测互感器的二次电流数字量输出,T为一个工频周波的时间,n为数据集计数序号,tn为一次电流第n个数据集采样完毕时间,k为叠加周期数,Ts为一次电流两个样本之间的时间间隔。
对于额定频率的相位和幅值误差,用以下2个复数系数表示:

幅值误差:
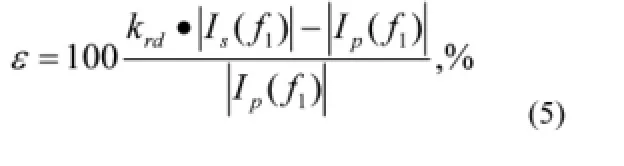
式中,krd为额定变比。相位误差:
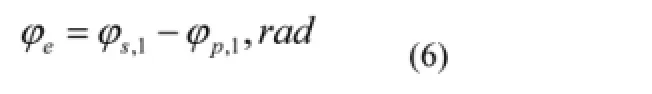
3 电子式电流互感器误差校验仪结构介绍
3.1试验电流源
作为校验过程中的信号源,电流源具备足够的容量及调节精度,频率调整范围为[49.5,50.5]Hz。
3.2标准电流互感器
铁芯线圈的电流互感器准确度较高,且不受一次载流导体位置影响,适合作为标准电流互感器。本系统采用的标准电流互感器额定变比为1000A/1A,准确度为0.05级。被测电子式电流互感器准确度为0.2S级。标准电流互感器的准确级比被测电子式电流互感器的准确级高2级,符合规范要求。
3.3信号调理电路
通过电阻分压电路将标准电流互感器低压侧的电流信号转换成电压信号,便于计算机处理。
3.4标准信号通道与被试信号通道
标准信号使用的数据传输通道有完善的屏蔽措施,可以忽略来自外界的干扰。被试信号使用的数据传输通道使用普通二次电缆,暴露在电磁干扰环境中,考虑工程实际中开关柜体尺寸,长度定为4m。
3.5数据采集卡
选用美国NI公司的PCI-4474完成标准电流互感器与被试电子式电流互感器的模数转换工作。其分辨率为24位,最小误差为6×10-8,满足校验仪在准确级方面的要求。在同步采样方面,PCI-4474使用外加时钟实现信号同步。由于基准信号和被试信号使用同一个数据采集卡完成信号处理,所以可以保证二者的采样同步性。
3.6基于LabVIEW的误差分析平台
计算机使用Winpcap软件捕获PCI-4474发出的数据包,通过LabVIEW建立的分析平台,在后台计算出电子式互感器的比值差、相位差;在前台实现标准、被测信号的波形显示等功能。

图1 校验仪结构图
4 合并单元主流数据处理算法分析
由于被试互感器的二次电缆暴露在强电磁干扰环境中,信号中含有大量噪声及谐波成分。因此要求合并单元算法能准确地提取出信号中的基频分量,这就需要分析不同信噪比背景下,合并单元常用的几种数据处理算法的优劣,得出能否克服干扰获得正确信号基频分量的结论。
合并单元常用的数据处理算法有:Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗、4阶矩形卷积窗和4阶三角自卷积窗函数。考虑到三角自卷积窗优良的旁瓣性能,本文重点介绍其实现流程,并就试验数据与其他窗函数对比、给出评价。
4.1基于三角自卷积窗的基波参数分析方法
4.1.1算法流程

图2 算法流程图
(1)对离散信号做截短处理,即进行长度为N的三角自卷积窗运算;(2)对加窗序列做傅氏变换,获得其离散频谱;(3)在得到的频谱中搜索基波附近局部幅值最大谱线k1和次大谱线k2;(4)利用LSM插值多项式求解频率偏移量λ;(5)由λ计算基波频率、幅值和初相角等参数。
4.1.2离散频谱插值算法
以频率单一的信号x(t)为例,经采样频率为fs的模数转换器后,得离散序列如下:

式中,A0、f0、φ0分别为信号的幅值、频率和初相角。
对离散后的信号加长度为N的p阶三角自卷积窗wTri-p(n)(n=0,1,…,N-1)进行截短,然后对截短序列进行傅氏变换,得到离散频谱为:
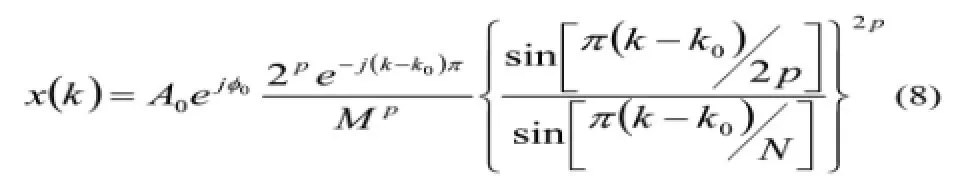
式中,k0=f0N/fs代表频率f0在离散频谱中的位置。在工程应用中,模数转换的采样频率fs为常数值,而电力系统的基波频率f0往往存在波动。所以就算采用锁相环技术,采样频率fs也无法与基波频率f0保持严格的整数倍关系,即k0为非整数,位于离散频谱幅值最大谱线k1和次大谱线k2之间(k1≤k0≤k2=k1+1)。因此非同步采样在所难免,如下图所示。
在频率f0附近采用局部峰值搜索策略找到局部幅值最大和次大的谱线位置,分别为k1和k2。两条谱线幅值分别为y1和y2。定义系数α为:
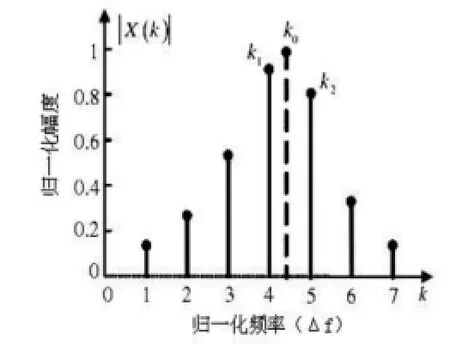
图3 非同步采样情况

定义系数β为:

由y1和y2可以计算出β,再利用频谱插值多项式计算出相应的α。此时,频率f0的计算式为:

幅值为:
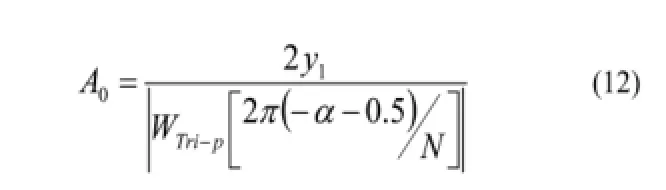
初相角为:

式(13)的arg表示求离散谱线的相角。
4.2噪声影响下的基波参数提取试验
令信号源产生电子式电流互感器的额定电流信号,该信号同时含有基波、2次和3次谐波,使电子式电流互感器输出信号的时域表达式为:

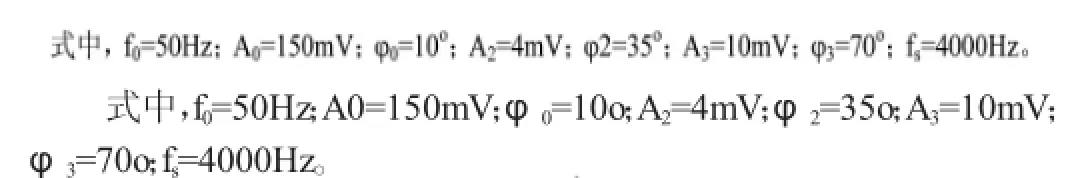

图4 基波频率绝对误差
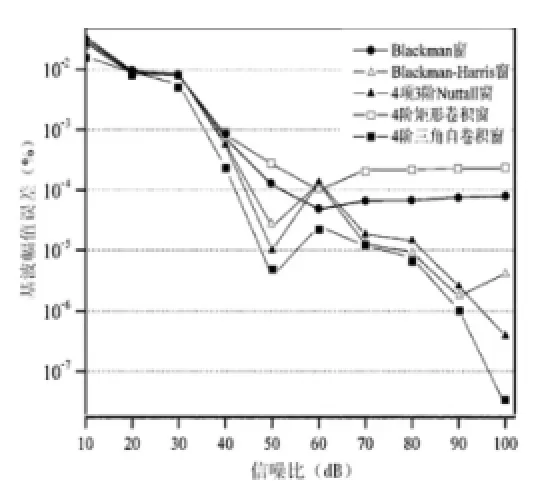
图5 基波幅值误差

图6 基波初相角绝对误差
为分析合并单元常用的算法在噪声的影响下,提取基波参数的准确度,我们将校验仪置于工频、辐射混合电磁场中,使被试信号通道中产生噪声。令信噪比以10dB为步长,在[10,100]dB的范围内变化,对被试信号持续采样。分别采用长度为N=512的Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗、4阶矩形卷积窗和4阶三角自卷积窗处理信号,并采用离散频谱插值校正算法求取信号的基波频率、幅值和初相角。各算法获取的基波参数随噪声强度变化的曲线分别如图4~图6所示。
图4展示了合并单元的几大常用算法在不同信噪比的噪声环境中,提取基波频率的绝对误差分布曲线。4阶矩形卷积窗与Blackman窗所采集的基波频率误差相似,略高于其他三类算法的测量误差;4项3阶Nuttall窗和Blackman-Harris窗在信噪比大于50dB后的测量结果准确度得到明显提高;使用4阶三角自卷积窗测得的基波频率准确度最高,且其优势在信噪比大于20dB后体现得淋漓尽致。
图5给出的是合并单元各常用算法在噪声环境中,提取基波幅值的比差分布曲线。在信噪比小于50dB时,各算法测得的基波幅值比差随信噪比的增大而迅速下降,但在[50,60]dB之间,Blackman-Harris窗、4项3阶Nuttall窗、4阶三角自卷积窗测量值的比差会有小幅上升,在信噪比大于60dB后,4阶矩形卷积窗与Blackman窗测量值的比差趋于常数,其他算法的误差则继续降低。在所有算法中,4阶三角自卷积窗的基波幅值比差最小。
图6给出了合并单元各常用算法在噪声环境中,提取基波初相角的绝对误差分布曲线。当信噪比不大于40dB时,4阶矩形卷积窗与Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗的误差相差不大,但均大于采用4阶三角自卷积窗测得基波初相角的绝对误差。当信噪比大于40dB时,Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗较4阶矩形卷积窗有明显优势,但准确度均低于采用4阶三角自卷积窗的情况。由图6可见,采用4阶三角自卷积窗的基波初相角准确度最高。
综上所述,4阶三角自卷积窗算法利用其优良的旁瓣性能,能够有效克服不同信噪比的噪声对基波参数分析的影响,其准确度高于采用Blackman窗、Blackman-Harris窗、4项3阶Nuttall窗、4阶矩形卷积窗的情况,特别当信噪比大于30dB后,采用4阶三角自卷积窗进行基波参数提取的准确度明显高于其它4种窗函数。
5 结语
本文介绍了电子式电流互感器误差校验仪的组成结构,建立了基于三角自卷积窗的FFT算法,还给出了基于三角自卷积窗的基波参数分析方法,并通过试验验证了合并单元各主流算法在基波参数分析中的有效性及准确性。
试验数据显示,合并单元各主流算法在不同强度的噪声影响下,测得的基波频率绝对误差变化范围为[3.8×10-9Hz,5.9× 10-4Hz];基波幅值比差变化范围为[3.1×10-8%,0.08%];基波初相角误差范围为[2.3×10-5’,3.1’]。符合GB20840.8-2007规定的0.2S级计量用互感器误差限制要求。故对于计量用电子式电流互感器,可以取消出口处的二次转换模块,合并单元的信号处理算法可以消除电磁干扰对数据精确度的影响。
[1]毛安澜,叶国雄,吴士普,等.Rogowski结构电子式电流互感器复合误差的检测方法[J].电测与仪表,2011,48(544):30-35.Mao Anlan,Ye Guoxiong,Wu Shipu,et al.The Method of Rogowski Structure of Electronic Current Transformer Composite Errors Calibration[J].Electrical Measurement&Instrumentation,2011,48(544):30-35(in Chinese).
[2]周文中,赵国生,李海洋.Rogowski线圈测量误差分析及改进措施[J].电力系统保护与控制,2009,37(20):99-103.Zhou Wenzhong,Zhao Guosheng,Li Haiyang.Error analysis and improved method ofRogowski coil[J].Power SystemProtection and Control,2009,37(20):99-103(in Chinese).
[3]江亚群,杨勇,姜燕.电参量微机测量中随机误差的分析及抑制[J].长沙电力学院学报(自然科学版),2002,17(4):34-37.Jiang Yaqun,Yang Yong,Jiang Yan.Methods of Restraning Random Eorrs in Computer-based Electirc Parameter Measurement[J].Journal ofChangSha University ofelectric power(Natural Science),2002,17(4):34-37(in Chinese).
[4]梁仕斌.电流互感器复合误差的测量方法[J].继电器,2005,33 (18):79-83.Liang Shibin.Measuring methods of composite errors on current transformer[J].RELAY,2005,33(18):79-83(in Chinese).
[5]尚秋峰,张静,董建彬.电子式电流互感器校准系统不确定度评定方法[J].电力系统自动化,2008,32(18):63-66.Shang Qiufeng,Zhang Jing,Dong Jianbin.Evaluation of Measurement Uncertainty for the Calibration System of Electronic Current Transformer[J].Automation of Electric Power Systems,2008,32(18):63-66 (in Chinese).
[6]童悦,张勤,叶国雄,等.电子式互感器电磁兼容性能分析[J].高电压技术,2013,39(11):29-35.Tong Yue,Zhang Qin,Ye Guoxiong,et al.Electromagnetic Compatibility Performance Of Electronic Transformer[J].High Voltage Engineering,2013,39(11):29-35(in Chinese).
[7]曹团结,尹项根,张哲等.电子式互感器数据同步的研究[J].电力系统及其自动化学报,2007,19(2):108-113.Tong Yue,Zhang Qin,Ye Guoxiong,et al.Electromagnetic Compatibility Performance Of Electronic Transformer[J].High Voltage Engineering,2013,39(11):29-35(in Chinese).
[8]方婵畅.电子式互感器数字量输出校验系统[D].武汉:华中科技大学,2011.
[9]胡浩亮,李前,卢树峰,等.电子式互感器误差的两种校验方法对比[J].高电压技术,2011,37(12):22-27.Hu Haoliang,Li Qian,Lu Shufeng,et al.Comparision of Two Electronic Transformer Error Measuring Methods[J].High Voltage Engineering,2011,37(12):22-27(in Chinese).
[10]李航康.电子式互感器误差校验的研究与实践[D].北京:华北电力大学,2013.
[11]谭洪恩,胡浩亮,雷民,等.电子式互感器现场校准技术实验分析[J].高电压技术,2010,36(12):90-95.
Tan Hongen,Hu Haoliang,Lei Min,et al.Experimental Analysis of On-site Calibration of Electronic Instrument Transformer[J].High Voltage Engineering,2010,36(12):90-95(in Chinese).
[12]曹津平.电子式互感器信号还原及测试技术的研究[D].北京:华北电力大学,2002.
[13]李振华.电子式互感器性能评价体系关键技术研究[D].武汉:华中科技大学,2014.
[14]赵应兵,周水斌,马朝阳.基于IEC61850-9-2的电子式互感器合并单元的研制[J].电力系统保护与控制,2010,38(6):104-106.Zhao Yingbing,Zhou Shuibin,Ma Zhaoyang.Research and manufacture ofmergingunit based on IEC 61850-9-2[J].Power System Protection and Control,2010,38(6):104-106(in Chinese).
[15]刘彬,叶国雄,郭克勤,等.基于Rogowski线圈的电子式电流互感器复合误差计算方法[J].高电压技术,2011,37(10):91-97.Liu Bin,Ye Guoxiong,Guo Keqin,et al.Calculation Method of Composite Error for Electronic Current Transformers Based on Rogowski Coil[J].High Voltage Engineering,2011,37(10):91-97(in Chinese).
[16]乔洪新,黄少锋,刘勇.基于二次插值理论的电子式互感器数据同步的研究[J].电力系统保护与控制,2009,37(15):48-52.Qiao Hongxin,Huang Shaofeng,Liu Yong.Discussion on data synchronization of electronic current transducer based on quadratic interpolation[J].Power SystemProtection and Control,2009,37(15):48-52 (in Chinese).
[17]全国互感器标准化技术委员会.GB/T 20840.8-2007互感器第8部分:电子式电流互感器[S].北京:中国国家标准化管理委员会,2007.
范巍(1984—),女,工程师,硕士,从事电力系统科技咨询工作。
兰春虎(1986—),男,助理工程师,硕士,从事电力系统保护及自动化设计工作。
王兆峰(1986—),男,高级工程师,硕士,从事电力系统保护及自动化设计工作。
