MMC电容电压开环预估及控制新方法

成佳富，陈洪胜，谢宁,周钦贤，李伟强

(1.广东电网有限责任公司惠州供电局，广东 惠州 516001；2.广东电网有限责任公司电力科学研究院，广东 广州 510080)



MMC电容电压开环预估及控制新方法

成佳富1，陈洪胜1，谢宁2,周钦贤1，李伟强1

(1.广东电网有限责任公司惠州供电局，广东 惠州 516001；2.广东电网有限责任公司电力科学研究院，广东 广州 510080)

对模块化多电平变换器(modular multilevel converter，MMC)的电容电压纹波进行了分析。针对开环调制中电容电压预估方法中含有积分环节，考虑估计所需电压电流信号中的谐波成分和干扰信号，直接积分运算受到影响，且存在积分初值选取和积分饱和等问题，提出两种改进的电容电压预估方法，即基于二阶广义积分的电容电压预估和基于双同步参考坐标系的电容电压预估方法。采用二阶广义积分器对输入的信号进行滤波，且不会对特定频率的信号幅值产生影响，可提高电容电压预估的准确性。在二倍频同步参考坐标系和基频同步参考坐标系上分别对上下桥臂电容电压之和与之差进行估计，避免了电容电压估计中的积分环节，适用于同步参考坐标系控制下的电压估计。最后，在PSCAD/EMTDC 环境中搭建的MMC仿真模型验证了所提方法的正确性和有效性。

模块化多电平变换器；电容电压预估；二阶广义积分；双同步旋转；开环调制

模块化多电平变换器(modular multilevel converter，MMC)具有结构模块化、输出特性好、冗余控制、可以独立地控制有功功率和无功功率等优点[1-4]。近年来，MMC以其优越的性能在柔性直流输电(high voltage direct current，HVDC)、静止同步补偿器、高压电机驱动、可再生能源发电并网和储能系统等中高压大功率场合得到越来越广泛的研究和应用[5-12]。MMC的三相并联连接在直流母线两端，各子模块电容处于悬浮状态，电容电压具有波动性；运行时各桥臂输出的电压不一致会引起三相之间的波动环流，由此增大器件的电流应力，并导致功率损耗增加，同时又会影响子模块电容电压产生，甚至影响系统稳定运行[13-17]。

已有很多文献对MMC环流控制开展了研究，文献[14]提出基于同步旋转坐标系的二次频环流控制方法，考虑环流中多次谐波分量的影响。文献[18]和[19]分别采用基于重复控制和准谐振控制对环流进行抑制。从调制策略上来说，直接调制所得的调制信号不包含电容电压的波动信息，各桥臂输出电压不一致，从而在三相间产生波动环流；采用电容电压实测值的闭环调制可以补偿电容电压波动的影响，但存在稳定性的问题，需要增加额外的控制维持稳定。文献[20]分别增加了上下桥臂能量差和电压差的外环控制来提高变换器的稳定性。文献[21]对MMC各桥臂能量进行估计，并计算出桥臂电容电压的估计值，提出基于桥臂电容电压估计值的开环调制策略。文献[22]建立了开环调制下MMC的内特性动态模型，分析了其稳定性和收敛率。文献[23]对开环调制策略进行了全局稳定性分析，但对电容电压的开环估计含有积分环节，考虑估计所需电压电流信号中的谐波成分和干扰信号，直接积分运算受到影响，且存在积分初值选取和积分饱和等问题。

本文针对开环调制中电容电压预估积分环节存在的问题，提出两种改进的电容电压预估方法：一是基于二阶广义积分的电容电压预估方法(the capacitor voltage estimated based on second order generalized integral，SOGI-CVE)，二阶广义积分器(SOGI)能够对输入的信号进行滤波，但又不会对特定频率的信号幅值产生影响，可以提高电容电压预估的准确性；二是基于双同步参考坐标系的电容电压预估方法(the capacitor voltage estimated based on double synchronous reference frame，DSRF-CVE)，在二倍频同步参考坐标系和基频同步参考坐标系上分别对桥臂电容电压之和与之差进行估计，避免了电容电压估计中的积分环节，适用于同步参考坐标系控制下的电压估计。最后，在PSCAD/EMTDC 环境中搭建MMC仿真模型验证了所提方法的正确性和有效性。

1 MMC数学模型

MMC拓扑结构示意图如图1所示。变换器有3个相单元，每相分为上下两桥臂，每个桥臂都由N个相同的子模块和桥臂电抗串联而成。图1中，R和L分别为MMC桥臂等效损耗电阻和桥臂电抗，C为子模块电容。根据图1所示电路结构，根据基尔霍夫定律建立方程，其中，ugx为网侧交流电压(x=a，b，c，下同)，isx为交流电流，icx为桥臂环流，uux和ulx分别为上、下桥臂输出电压，iux和ilx分别为上、下桥臂输出电流，udc和idc分别为直流侧电压和电流。

SM表示子模块，SM1和SMN分别表示第1个和第N个子模块。图1 三相MMC结构

(1)

(2)

定义变换器交流输出电压usx和桥臂内电势ucx为：

(3)

联立式(1)—(3)可得MMC外特性和内特性方程为：

(4)

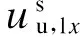
(5)

(6)

其中usx,ref和ucx,ref分别为usx和ucx的指令值。

令上下桥臂能量和与差分别为：

(7)

联立式(2)，(5)—(7)，可得桥臂能量和与差的方程：

(8)

2 电容电压波动估计

相比于直接调制，开环调制下根据电容电压估计值求取调制波，补偿了电容电压波动的影响。三相环流波动分量很小，可以忽略，因此可以认为环流中只含直流分量，用于环流抑制的桥臂内电势指令为零。设变换器交流输出电压指令和交流电流分别为：

(9)

(10)

(11)

(12)

2.1 基于二阶广义积分的电容电压预估方法(SOGI-CVE)

相对于直接积分法，二阶广义积分法可以对输入信号进行滤波，又不影响特定频率信号的幅值，在电网电压同步信号的提取中得到了广泛应用。SOGI的传递函数如下：

(13)

式中：s为传递函数变量符号；k为系统阻尼比。

式(8)给出了桥臂能量和与差的方程，以瞬时值进行估计时需要对方程右侧积分，直接对瞬时值进行积分容易受到信号中谐波和干扰信号的影响，导致估计结果不准确。根据式(12)可知能量和的波动分量为二倍频分量，而能量差的波动分量为基频分量，因此可以分别设计角频率为二倍和一倍电网频率的二阶广义积分器，提高电容电压估计值的准确性和抗干扰能力。

基于二阶广义积分的电容电压预估方法如图2所示。

图2 SOGI-CVE电容电压预估法

2.2 基于双同步参考坐标系的电容电压预估方法(DSRF-CVE)

对式(12)桥臂能量和与差波动分量进行积分得：

(14)

(15)

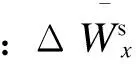
平衡状态下，三相桥臂能量之和的波动分量为二倍频负序波动，而桥臂能量之差的波动分量为基频正序波动。分别将式(14)和式(15)三相静态波动分量转换至二倍频负序和基频正序同步参考坐标系，可得能量静态波动分量在同步参考坐标系上的表达式，即

(16)

(17)

其中，K=-udc/4ω，A=1/2ω，B=2Icx0/ω，旋转变换矩阵

(18)

式中θ分别等于2ωt和ωt。

根据式(16)和式(17)可知，可以先求解桥臂能量和在二倍频负序同步参考坐标系上的静态分量，以及桥臂能量差在基频正序同步参考坐标系上的静态分量，再经旋转变换得到三相桥臂能量和与差的静态分量。

其中θ=2ωt。

其中θ=ωt。

结合式(5)和式(7)可得上下桥臂电容电压波动分量估计值：

(21)

图3 DSRF-CVE电容电压预估法

3 MMC变换器整体控制

基于电容电压预估的MMC控制策略中，输出电流控制与传统的两电平VSC电流控制类似，采用基于dq同步参考坐标系的解耦控制方法。控制框图如图4(a)所示。基于电容电压预估值的开环调制可以有效地抑制环流电流，为维持系统稳定，并有效地控制环流，本文设计了采用准谐振控制器的环流控制方法。准谐振控制器的传递函数

(22)

式中：kr为积分系数；kp为比例系数；ωc为截止频率；ω0为谐振频率。

环流电流PIR控制框图如图4(b)所示。基于电容电压预估的开环调制策略如图4(c)所示。交流电流控制和环流控制得到输出电压指令经计算最终可得上下桥臂输出电压参考值，结合电容电压预估值对输出电压参考值进行归一化处理得到变换器上下桥臂的调制信号。不同于直接调制方式，开环调制采用电压预估值进行归一化处理，得到的调制信号中含有二倍频波动信息，补偿了电容电压波动的影响，因而可以有效地抑制环流电流中的谐波分量。

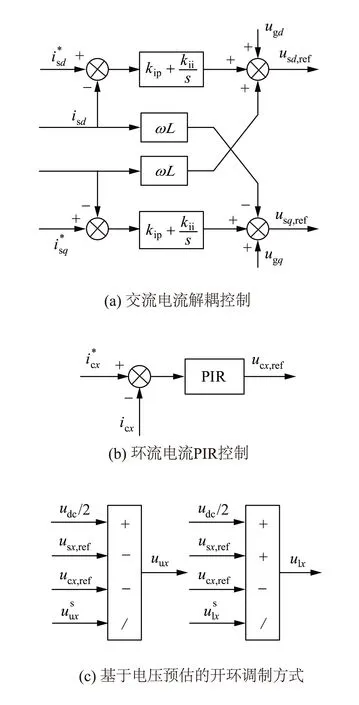
L—电抗值；kip—比例系数；kii—积分系数。图4 MMC变换器控制框图

4 仿真验证

在PSCAD/EMTDC 环境中搭建如图5所示的MMC仿真模型，验证本文所提控制策略的正确性，仿真参数见表1。

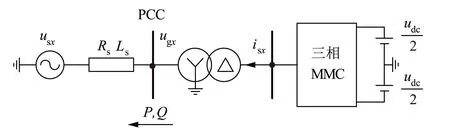
P、Q分别为有功功率和无功功率。图5 MMC仿真模型

为验证本文所提电容电压预估方法的正确性，搭建了采用直接调制方式的MMC控制模型，其中输出电流控制采用解耦控制方法，环流电流控制采用PIR控制器，得到实际电容电压波形及本文所提DSRF-CVE电压预估法、SOGI-CVE预估法及直接延时移相π/2法得到的电压波形，如图6所示。

表1 仿真参数表

项目数值项目数值额定有功功率/MW15交流系统电压/kV35变压器变比35kV/13.8kV直流侧电压/kV25桥臂电感/mH6桥臂子模块数4子模块电容/μF2500

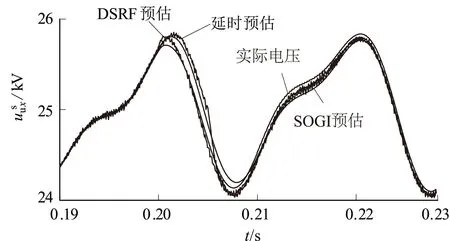
图6 电容电压实际值与预估值

为对比3种电压预估方法的性能，同时消除有功功率跳变对电压控制产生的影响，设定0.2 s时无功功率指令由0 Mvar阶跃至2 Mvar。可知，静态过程中，DSRF-CVE电压预估法和延时移相π/2法得到的电压预估波形中含有大量高频谐波，而SOGI-CVE电压预估法得到的电压预估波形平滑，抑制了谐波对电压预估值的影响。动态过程中，DSRF-CVE的动态响应时间短为0.002 s，而SOGI-CVE和延时移相π/2的动态响应时间约为0.01 s。

根据理论推导及仿真分析可知，采用SOGI-CVE电压预估法可以有效地消除谐波及干扰信号的影响，提高了电容电压预估的准确性，但动态过程中存在较大延时。而采用DSRF-CVE电压预估法无法消除桥臂输出电压信号中的高次谐波的干扰，但动态响应速度快，且该方法避免了电容电压估计中使用的积分环节，不需要考虑积分初值选取和积分饱和等问题，由于其需桥臂输出电压的dq轴信号，适用于同步参考坐标系控制下的电压估计。

采用DSRF-CVE电压预估方法搭建MMC开环调制仿真模型，仿真波形如图7所示。MMC工作在额定工况，1 s时功率由15 MW变化至-15 MW， 无功功率保持为0。图7(a)所示为MMC有功、无功功率变化曲线，图7(b)所示为U相上下桥臂电容电压实际值与预估值波形，图7(c)为变换器输出交流电流波形，三相电流波形正弦，谐波含量低。图8(a)和(b)分别为采用开环调制和直接调制时变换器三相环流波形，可知相比于直接调制，开环调制具有更好的谐波抑制效果及动态响应性能。

图7 采用DSRF-CVE电压预估法仿真波形

图8 环流波形对比

5 结束语

本文针对开环调制中电容电压预估积分环节存在的问题，提出两种改进的电容电压预估方法。基于二阶广义积分的电容电压预估方法(SOGI-CVE)，二阶广义积分器(SOGI)能够对输入的信号进行滤波，可以有效地消除谐波及干扰信号的影响，提高了电容电压预估的准确性；基于双同步参考坐标系的电容电压预估方法(DSRF-CVE)，虽无法消除桥臂输出电压信号中的高次谐波的干扰，但可避免电容电压估计中的积分环节，不需要考虑积分初值选取和积分饱和等问题，适用于同步参考坐标系控制下的电压估计。

[1] DEBNATH S, QIN Q C, BAHRANI B. Operation, Control, and Applications of the Modular Multilevel Converter: A Review[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 37-53.

[2] PEREZ M, BERNET S, ROFRIGUEZ J, et al. Circuit Topologies, Modeling, Control Schemes, and Applications of Modular Multilevel Converters[J]. IEEE Transactions on Power Electronics, 2015, 30(1):4-17.

[3] FAN S F, ZHANG K, XIONG J. An Improved Control System for Modular Multilevel Converters with New Modulation Strategy and Voltage Balancing Control[J]. IEEE Transactions on Power Electronics, 2015, 30(1):358-371.

[4] ZHOU Y B, JIANG D Z, HU P F. A Prototype of Modular Multilevel Converters [J]. IEEE Transactions on Power Electronics, 2014, 29(7):3267-3278.

[5] 周月宾，黎小林，许树楷.基于子模块电压估计的MMC调制与控制[J].南方电网技术，2015，9(9)：23-29.

ZHOU Yuebin, LI Xiaolin, XU Shukai. MMC Scheduling and Control Based on Modular Voltage Estimation[J]. Southern Power System Technology, 2015，9(9)：23-29.

[6] 李文津，汤广福，康勇，等．基于VSC-HVDC的双馈式变速恒频风电机组启动及并网控制[J].中国电机工程学报，2014(12)：1864-1873.

LI Wenjin, TANG Guangfu, KANG Yong, et al.Starting up and Integration Control of Doubly-fed Variable-speed Constant-frequency Wind Power Generator Based on VSC-HVDC[J]. Proceedings of the CSEE,2014(12):1864-1873.

[7] 李岩，罗雨，许树楷，等.柔性直流输电技术：应用、进步与期望[J].南方电网技术，2015，9(1)：7-13.

LI Yan, LUO Yu, XU Shukai, et al. VSC-HVDC Transmission Technology: Application,Advancement and Expectation[J]. Southern Power System Technology, 2015,9(1):7-13.

[8] ANTONOPOULOS A, ANGQUIST L, HARNEFORS L, et al. Optimal Selection of the Average Capacitor Voltage for Variable-speed Drives with Modular Multilevel Converters[J]. IEEE Transactions on Power Electronics, 2015, 30(1):227-234.

[9] 韦延方，卫志农，孙国强，等. 适用于电压源换流器型高压直流输电的模块化多电平换流器最新研究进展[J]. 高电压技术，2012，38(5)：1243-1252.

WEI Yanfang，WEI Zhinong，SUN Guoqiang，et al. New Prospects of Modular Multilevel Converter Applied to Voltage Source Converter High Voltage Direct Current Transmission[J]. High Voltage Engineering，2012，38(5)：1243-1252.

[10] 唐庚，徐政，薛英林. LCC-MMC混合高压直流输电系统[J]. 电工技术学报，2013，28(10)：301-310.

TANG Geng，XU Zheng，XUE Yinglin. A LCC-MMC Hybrid HVDC Transmission System[J]. Transactions of China Electrotechnical Society，2013，28(10)：301-310.

[11] 徐政，薛英林，张哲任. 大容量架空线柔性直流输电关键技术及前景展望[J]. 中国电机工程学报，2014，34(29)：5051-5062. XU Zheng，XUE Yinglin，ZHANG Zheren. VSC-HVDC Technology Suitable for Bulk Power Overhead Line Transmission[J]. Proceedings of the CSEE，2014，34(29)：5051-5062.

[12] 滕松，宋新立，李广凯，等. 模块化多电平换流器型高压直流输电综述[J]. 电网与清洁能源，2012，28(8)：44-50.

TENG Song，SONG Xinli，LI Guangkai，et al. A Survey on HVDC Transmission with Modular Multilevel Converters [J]. Power System and Clean Energy，2012，28(8)：44-50.

[13] QIN Q C, SAEEDIFARD M. Reduced Switching-frequency Voltage-balancing Strategies for Modular Multilevel HVDC Converters[J]. IEEE Transactions on Power Delivery, 2013,28(4):2403-2410.

[14] TU Q R, XU Z, XU L. Reduced Switching-frequency Modulation and Circulating Current Suppression for Modular Multilevel Converters[J]. IEEE Transactions on Power Delivery,2011,26(3):2009-2017.

[15] 管敏渊，徐政．MMC型VCS-HVDC系统电容电压的优化平衡控制[J].中国电机工程学报，2011，31(12)：9-14.

GUAN Minyuan, XU Zheng. Optimized Capacitor Voltage Balancing Control for Modular Multilevel Converter Based VSC-HVDC System[J].Proceedings of the CSEE,2011，31(12)：9-14.

[16] DARUS R, POU J, KONSTANTINOU G. A Modified Voltage Balancing Algorithm for the Modular Multilevel Converter: Evaluation for Staircase and Phase-disposition PWM[J]. IEEE Transactions on Power Electronics, 2014,99(8):1-8.

[17] 赵昕，赵成勇，李广凯，等．采用载波移相技术的模块化多电平换流器电容电压平衡控制[J].中国电机工程学报，2011，31(21)：48-54.

ZHAO Xin, ZHAO Chengyong, LI Guangkai, et al. Submodule Capacitance Voltage Balancing of Modular Multilevel Converter Based on Carrier Phase Shifted SPWM Technique[J].Proceedings of the CSEE,2011,31(21):48-54.

[18] HE L Q, ZHANG K, XIONG J. A Repetitive Control Scheme for Harmonic Suppression of Circulating Current in Modular Multilevel Converters [J]. IEEE Transactions on Power Electronics,2015,30(1): 471-481.

[19] LI S H, WANG X L, YAO Z Q. Circulating Current Suppressing Strategy for MMC-HVDC Based on Non-ideal Proportional Resonant Controllers Under Unbalanced Grid Conditions [J]. IEEE Transactions on Power Electronics, 2015,30(1):387-397.

[20] ANTONIOS A, LENNART A, HANS P N. On Dynamics and Voltage Control of the Modular Multilevel Converter [C]//13th European Conference on Power Electronics and Applications, EPE ’09. Barcelona, Spain:[s.n.],2009.

[21] LENNART A, ANTONIOS A, HANS P N.Open-loop Control of Modular Multilevel Converters Using Estimation of Stored Energy [J]. IEEE Transactions on Industry Application,2011,47(6):2516-2524.

[22] LENNART A,ANTONIOS A, HANS P N.Dynamic Analysis of Modular Multilevel Converters [J]. IEEE Transactions on Industrial Electronics,2013,60(7):2526-2537.

[23] ANTONIOS A, LENNART A, HANS P N.Global Asymptotic Stability of Modular Multilevel Converters [J]. IEEE Transactions on Industrial Electronics,2014,61(2):603-612.

(编辑 查黎)

New Methods for Estimation and Control on MMC Capacitor Voltage Open-loop

CHENG Jiafu1, CHEN Hongsheng1, XIE Ning2, ZHOU Qinxian1, LI Weiqiang1

(1.Huizhou Power Supply Bureau of Guangdong Power Grid Co., Ltd., Huizhou, Guangdong 516001, China; 2. Electric Power Research Institute of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510080, China)

This paper analyzes ripple wave of capacitor voltage of modular multilevel converter (MMC). In allusion to problems such as integration element in capacitor voltage estimate (CVE) in open-loop modulation, consideration of harmonic and interference signals in voltage current signals, direct integral operation being affected, selection for integration initial value and integral saturation, and so on, two kinds of improved estimation methods for capacitor voltage are presented, one is CVE based on the second order generalized integral (SOGI-CVE) and the other is based on double synchronous reference frame (DSRF-CVE). It will not affect signal amplitude of specific frequency by using the second order integrator to filter input signals and can improve veracity of CVE. It can also avoid integration element in CVE by estimating sum or difference of capacitor voltage of the upper and lower bridge arms on the second harmonic frequency synchronous reference frame and fundamental frequency synchronous reference frame, which is suitable for voltage estimation under the control of synchronous reference frame. In PSCAD/EMTDC environment, a MMC simulation model is established to verify validity and effectiveness of proposed methods.

modular multilevel converter (MMC); capacitor voltage estimate; the second order generalized integral ( SOGI); double synchronous rotation; open-loop modulation

2016-06-02

10.3969/j.issn.1007-290X.2016.10.015

TM721

A

1007-290X(2016)10-0085-07

成佳富(1988)，男，湖南永州人。工学硕士，从事继电保护技术、柔性输配电技术和电能质量控制技术研究。

陈洪胜(1978)，男，广东揭阳人。工程师，工学学士，主要从事自动化、多电平变换器控制技术和电能质量控制技术研究。

谢宁(1988)，男，山东菏泽人。工程师，工学博士，主要从事谐波抑制与无功补偿、大型光伏电站并网技术、多电平变换器技术研究。