基于CFD原理的架空输电线路故障概率估算方法

胥志强, 吴杰康

(广东工业大学 自动化学院，广东 广州 510006)



基于CFD原理的架空输电线路故障概率估算方法

胥志强, 吴杰康

(广东工业大学 自动化学院，广东 广州 510006)

针对雷击、风速、覆冰、污闪、鸟类接触、线路舞动和老化等对架空输电线路安全稳定运行的影响，对架空输电线路故障率预测模型进行探讨。首先将架空输电线路的故障率流态化，考虑各种不确定性因素影响，并加权优化相关的影响因子，以求解出其综合健康指数，同时修正输电线路的流态故障概率分布，以此建立受多因素影响的架空输电线路故障率预测模型；再由有限体积法(finite volume method，FVM)对该模型进行网格划分，并对其采用计算流体动力学(computational fluid dynamics，CFD)原理模拟仿真，根据所得结果估算出具有高准确度的预测值。以IEEE 9、IEEE 30、IEEE 57、IEEE 118为实例进行计算和分析，结果表明所研究模型可以有效地提高线路故障率的预测精度，验证了CFD模拟仿真在求解架空输电线路失效率问题时的有效性。

架空输电线路；流态故障率；综合健康指数；有限体积法；计算流体动力学

架空输电线路是电力系统输送电能的主要途径，其运行状态对正常生产生活和电力系统的安全稳定运行有极大影响，但大部分输电线路处于荒郊野外，工作环境较为复杂，其故障率的随机波动性较大，且引起输电线路故障的主要因素有雷击、风速、覆冰、污闪、鸟类接触、线路舞动和老化及国家政策等。为了能够快速准确地判断出输电线路的故障率，积极采取防护和维修措施，以期故障损失最小化，马尔可夫法[1]、状态枚举法[2]和人工智能算法[3]等故障率预测方法已应用到该领域。大量研究发现：输电线路跨越茂密的林区、鸟类活动等对其运行状态会产生极大的干扰[4-5]；不同的气候条件对其故障率的预测结果存在较大的影响，气温变化、雷击现象和线路舞动使线路故障率显著上升[6-8]，大面积覆冰有碍于输电线路正常运行，影响人们的正常生活和生产秩序[9-10]；线路绝缘老化使其电气性能劣化导致失效[11]。然而，传统的架空输电线路故障概率预测模型和方法已日益捉襟见肘：蒙特卡洛法预计故障率时需要足够长的重复周期，其收敛时间受到限制；状态枚举法则需要消耗较多的CPU时间，且当线路元件数量较多又相互影响时易导致预测结果产生很大误差；而人工智能算法亦存在着收敛速度慢和易陷入局部极小点，甚至不能收敛等缺点。此外，当前的架空输电线路故障率随机性强，大量的预测模型和方法所需考虑的内容尚需进一步完善，故需通过建立合理全面的故障率预测模型、改进预测方法，提高线路失效预测的准确率，再以此为基础采取一定的保护和维修措施，从而保证整个电力系统安全可靠运行。

本文针对常规输电线路故障率预测模型及方法的不足，综合考虑雷击、风速、覆冰、污闪、鸟类接触、线路舞动和老化等综合影响因素，以此为基础建立了多因素综合影响的架空输电线路故障率预测模型，由有限体积法(finite volume method，FVM)对其进行网格划分，再通过计算流体动力学(computational fluid dynamics，CFD)非线性数值模拟其运行状态，进而估算出不确定性因素对线路故障的影响。考虑到CFD模拟具有物理概念明晰、理论根据充分、计算速度快和预算结果可靠等特点，可有效解决受复杂因素约束的线路故障率优化计算问题，故选取CFD对所建优化模型进行求解，并针对IEEE 9、IEEE 30、IEEE 57和IEEE 118分别进行仿真分析，来验证该理论的有效性和所建模型的正确性。

1 CFD原理

1.1 基本理论

CFD原理是通过计算机数值计算和图像显示，对包含有流体流动和热传导等相关物理现象的系统所做的分析[12-13]，其基本思想如下：把原来在时间域和空间域上连续的物理量场，用一系列离散点上的变量值的集合来替代，并通过一定的原则和方式建立起反映这些离散点上场变量之间关系的代数方程组，然后求解代数方程组获得场变量的近似解。

CFD原理的架空输电线路故障概率估算方法CFD是在流动基本方程(质量守恒方程、动量守恒方程、能量守恒方程)控制下对流体流动过程进行的数值模拟，由此得到极其复杂流场内各个位置上的基本物理量(如速度、压力、温度、浓度等)的分布，以及这些物理量随时间的变化情况。

任何流的问题都必须满足质量守恒定律：单位时间内流体微元中质量的增加等于同一时间间隔内流入该微元体的净质量。

(1)

引入矢量符号

(2)

则(1)式可改写成

(3)

式(1)至(3)中：ρ为流体密度；t为时间；u为速度矢量；u、v和w是速度矢量u在x、y和z方向上的分量。若流体不可缩放，且其密度ρ为常数，则可得出

(4)

任何流动系统都必须满足动量守恒定律：微元体中流体的动量对时间的变化率等于外界作用在该微元上的各种力之和。由此导出x、y和z三个方向的动量守恒方程：

(5)

式中：p为微元体上的压力密度；τxx、τxy和τxz分别为微元体分子因粘性作用在其表面上产生的粘性应力τ的分量；Fx、Fy和Fz分别为微元体上的体力在x、y和z三个方向上的分力。若体力只有重力，且为轴竖直方向，则Fx=0、Fy=0、Fz=-ρg。

能量守恒定律是包含有热交换的流动系统必须满足的基本定律：微元体中能量的增加率等于进入该微元体的净热流量加上体力和面力对其所做的功。则

(6)

式中：cp是流体比热容；T是流体热力学温度；k为流体的传热系数；ST为粘性耗散项，包括流体的内热源及由于粘性作用流体机械能转换为热能的部分。

1.2 基于CFD原理预测架空输电线路故障率

架空输电线路故障概率的常规预测方法已难于适用日渐庞大的电力系统，其预测结果的可靠度面临巨大的挑战。为了有效克服常规输电线路故障率预测模型及方法的不足，尽可能地提高预测结果的准确度，本文提出了基于CFD原理的输电线路故障率预测模型，通过精细的流场计算准确模拟历史数据不足、地形复杂、气候多变的户外线路故障率流动特征，尽可能地提高预测结果的准确度。

不确定性CFD模拟方法是随机分析方法和传统CFD方法的有机结合。传统随机分析的方法有采样法、微扰动法、敏感性分析、模糊逻辑法等。其中敏感性分析、模糊逻辑法通常敏感性分析不能给出精确的量化的随机响应；而蒙特卡洛(Monte Carlo)方法由于结构简单而应用较为广泛，但其效率较低：在处理低维度问题时，蒙特卡洛方法仍需要大量的样本，对计算资源的消耗较大。微扰动法只适合随机变化很小的情况。大多数CFD模拟所釆用的数学模型都是确定性的，物性参数、几何模型和边界条件等也都是确定性的，并以寻求确定性解为目标，同时κ-ε以及κ-ω模型计算结果也显示了不错的预测精度。

本文在已知整个线路系统的总体故障率的前提条件下，通过参阅有关文献选用κ-ε数学模型，根据预测目标函数和约束条件调整其物性参数、边界条件等。设输电线路故障率的约束因素q有m个，其相应影响程度为θi(i=1,2,…,m)，则输电线路节点x处的修正因子

(7)

预测模型的修正因子向量为P=[ζ1,ζ2,…,ζk]，其中k≤q，其数学表达式为

(8)

若各约束因素的拟合残差

(9)

式中n指不同时刻。则其构成的拟合残差矩阵

(10)

通过求解出κ-ε数学预测模型的最优修正因子向量，其目标函数和约束条件为：

(11)

令R=[1,1,…,1]，则有

(12)

用拉格朗日乘子法求解上式，得：

(13)

则最优修正因子向量

(14)

目标函数的最小值

(15)

首先设定故障率通过每个负荷输入端口均匀输入线路系统，再由每个负载端口均匀输出。假设每一条输电线路均是具有有效断面面积的中空管道，故障率以均匀流态(流体密度ρ0为定值)的形式分布于其中，则长度为x+dx位置处的流态故障率

(16)

式中：ξx为修正因子；vx为线路管内流态故障率的流速；Sx为有效断面面积；dx为x处线路段的微小长度；V0为线路中流体总体积；λ0为线路总故障。

通过修正因子修正由CFD预测线路在节点x处的流态故障率流速，结合输电线路的仿真模型，由流动方程求解出线路各节点处的等效流速vi，再联立相关公式可计算出输电线路任何节点处的故障概率。其中每个约束因素的影响程度可由基于切比雪夫正交基神经网络预测的综合健康指数来逼近。

2 架空输电线路的流态故障概率建模

为了能够有效利用CFD数值模拟工具准确预计输电线路故障率，本文首先将线路的故障率流态化，由此引入两个新概念。

a) 流态故障概率λ：是描述输电线路产生随机性故障的概率值。将输电线路故障率流态化，能够准确反映故障率的随机性特点，提高预测结果的可靠性。

b) 综合健康指数Ω(Ω是一无量纲系数，通常情况下Ω>1)：是描述输电线路受多种复杂影响因素约束条件下发生故障程度的数值。任意电力系统中的输电线路故障率都由多因素综合影响造成的，故不同线路上的故障率分布情况也迥异，需要综合健康指数修正其流态故障率的分布，以期保证预测结果有较高的准确度。

综合健康指数Ω的数学表达式为

(17)

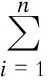
本文通过构造切比雪夫正交基神经网络[14]，快速有效地学习给定样本并逼近目标函数，实现对输入输出关系的最小平方误差逼近，求解出最优权重系数，其模型如图1所示。

以切比雪夫正交多项式函数ki(t)作为隐层神经元的激励函数，对未知函数K(t)进行学习与逼近，可得该网络权值的矩阵向量迭代计算公式为

(18)

式中：X为输入整合矩阵；δ为学习步长，且δ>0；σ为输出向量，σ∈Rm。其中有

则该切比雪夫正交基神经网络的最优权值

(19)

考虑到多种复杂影响因素约束输电线路的故障率分布，其总体影响由综合健康指数进行修正；再采用CFD方法对流态故障率进行数值模拟，可以有效改善预测结果的准确性，其具体建模步骤如图2所示。

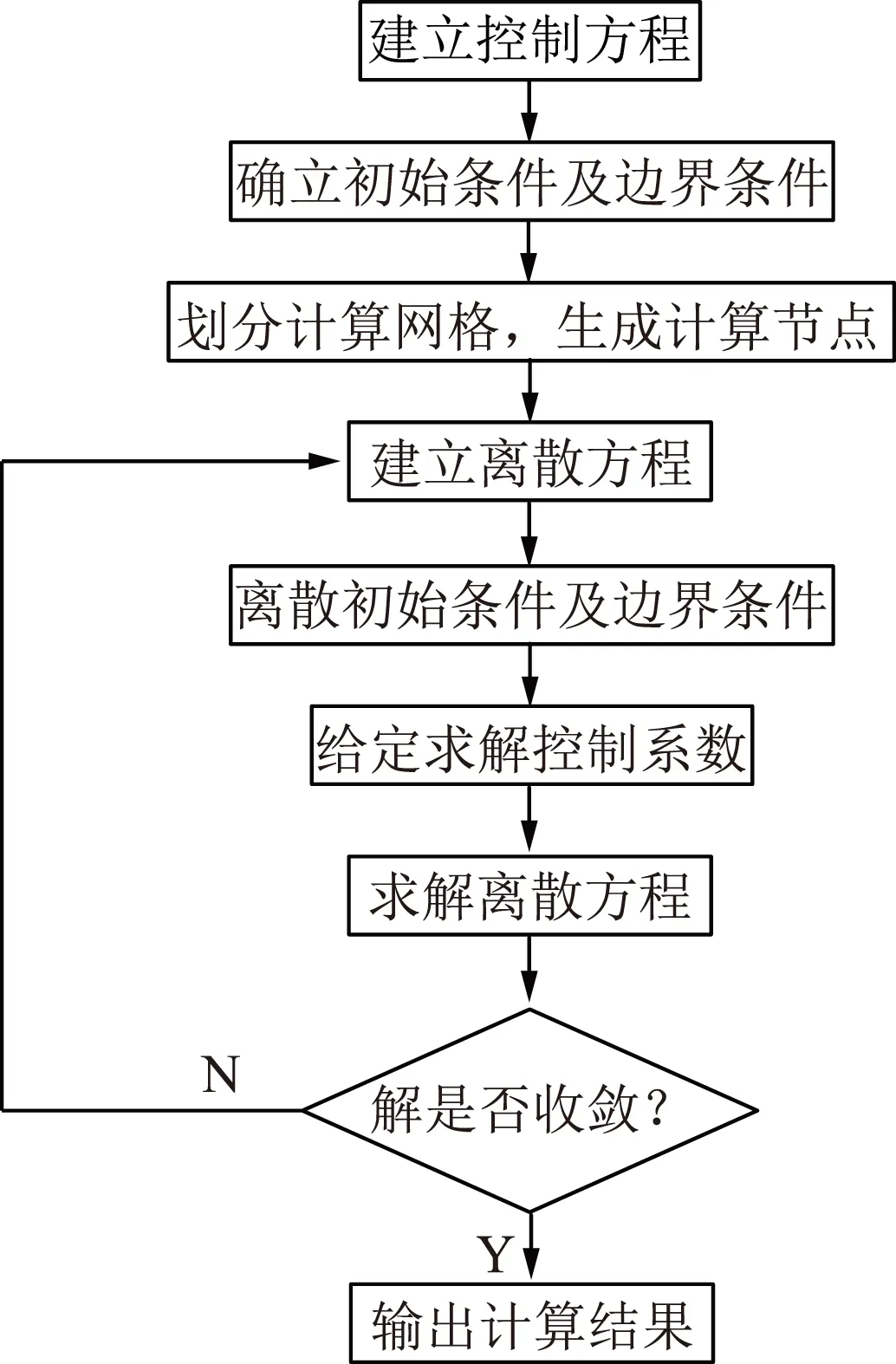
图2 CFD模拟工作流程

在建模过程中划分网格，建立离散方程非常关键，直接影响所建模型预测结果的精确度。利用FLUENT求解控制方程时，一般采用网格生成技术将控制方程在空间区域上进行离散，但由于所处理问题自身的复杂性，常采用FVM对所得到的离散方程组进行求解。

FVM原理是将计算区域划分为一系列控制体积，将待解微分方程对每一个控制体积积分得出离散方程[15]，其基本思路是：将计算区域划分为网格，并使每个网格点周围有一个互不重复的控制体积；将待解微分方程(控制方程)对每一个控制体积积分，从而得出一组离散方程，其关键是在导出离散方程中，需要对界面上的被求函数本身及其导数的分布作出某种形式的假定。

3 架空输电线路的流态故障率估算

本文先将线路故障率流态化，联立式(17)和式(19)，求解获得综合健康指数和最优权重序列，并以此修正线路的流态故障率分布，再通过CFD模拟及分析电力系统t时刻的速度矢量分布图，得出该时刻各节点处的流态故障率计算公式为

(20)

式中：λi,t为t时刻i节点处的失效率；vi,t为t时刻i节点处的流态故障率等效流动体的流速；Si,t为t时刻i节点处的等效断面面积；Ωi,t为t时刻i节点处的综合健康指数；λa,t为t时刻系统的总实际故障率；Va,t为t时刻系统中的总流态故障率等效流动体体积。

各节点处的等效断面面积及半径分别为：

(21)

式中：Si为i节点处的等效断面面积；Ri为i节点处的等效半径；Ai为流体在i节点处的实际流动断面面积；Li为i节点处的实际流动断面湿周。

4 实例仿真

本文基于CFD原理的架空输电线路故障概率预测模型，在已知电力系统总故障率的前提下，针对IEEE 9、IEEE 30、IEEE 57和IEEE 118中各线路故障率的分布分别进行CFD仿真分析，各节点系统的具体原始数据详见表1，于每个系统中随机选取10处线路节点为故障率预测点，以其实际故障率为参考数据，根据所得模拟结果对比分析。

首先，由表1中4个电力系统的架空输电线路原始数据，通过Gambit软件绘制出其模型结构示意图，如图3所示。根据系统论证资料，本文所述系统均采用LGJ-185型钢芯铝绞线，查得LGJ-185的计算直径为19 mm。由于线路截面呈圆形对称结构，故图中只描绘了半个输电线路模型的内部结构。

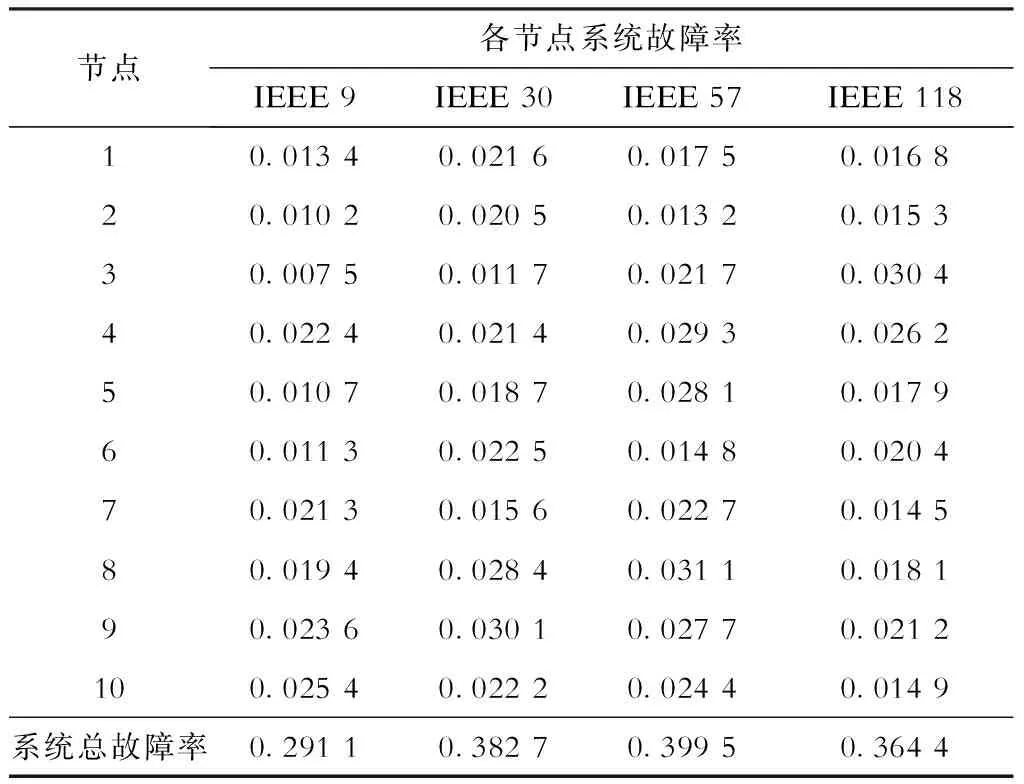
表1 各节点系统的相关故障率原始数据

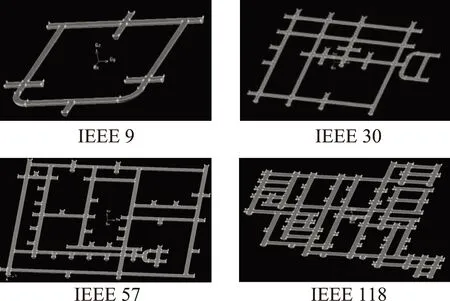
图3 各节点系统模型结构

其次，网格是CFD模型的几何表达式，也是模拟与分析的载体。网格质量的高低对CFD计算精度和计算效率具有重要影响。对于复杂的CFD问题，网格生成极为重要，恰当的网格分布与流态故障率的流动方向吻合性较好，可以有效地降低其数值耗散，故必须给予足够的重视。通过多次调和得到各节点系统的网格形状如图4所示。

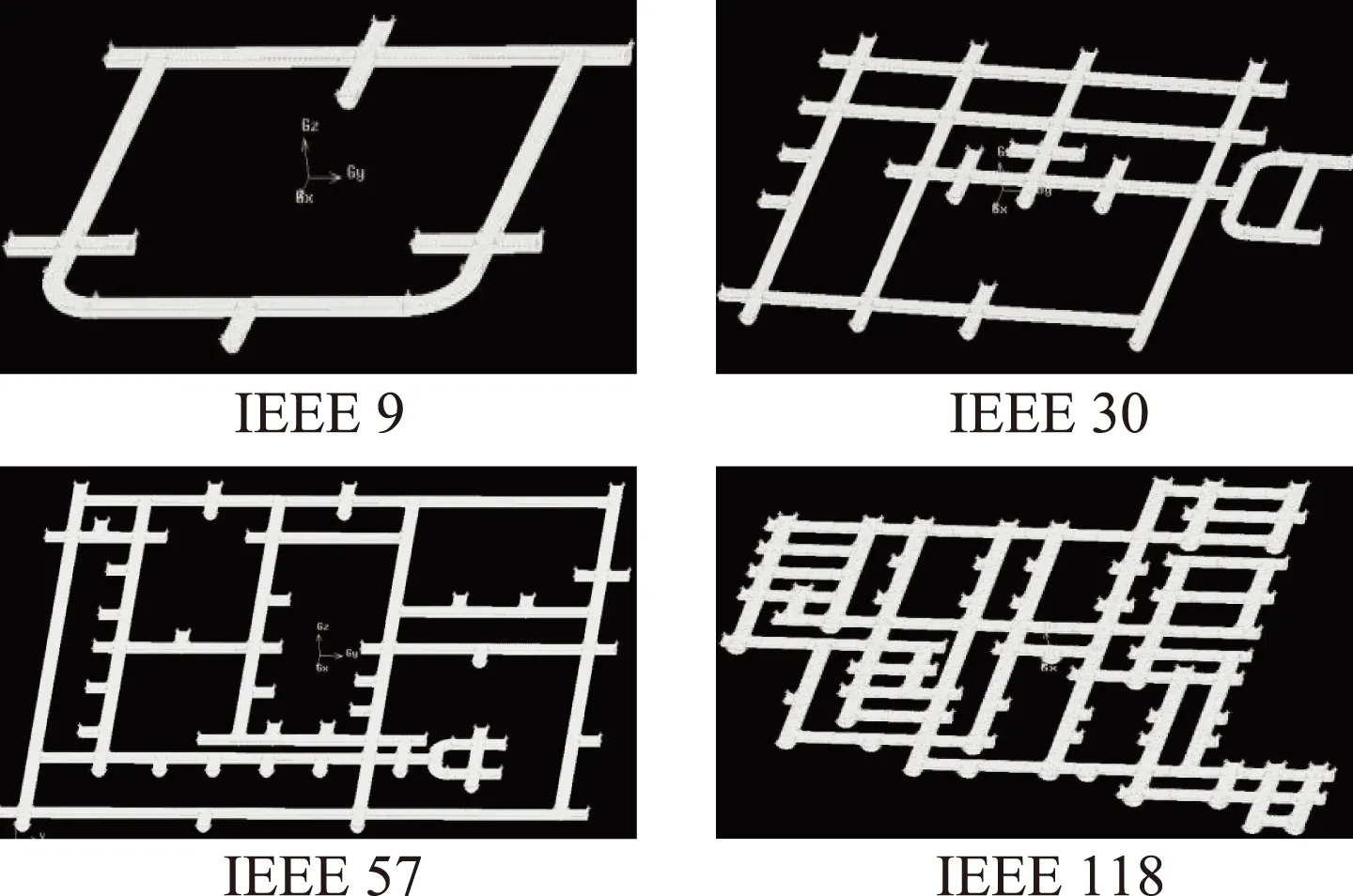
图4 各节点系统网格

再次，对所建模型输入相关的原始数据，为了能够准确模拟出流态故障率的动态非线性分布状况，故设定其迭代次数为500进行迭代分析。同时设定置信区间为[0.999 0，0.999 5]，其中IEEE 9、IEEE 30、IEEE 57、IEEE 118节点系统迭代次数分别为472、386、372、256。经过对各节点系统的残差检测结果分析得出：采用CFD模拟预测结果的可靠度均较高，达到了99.9%以上，有时其准确性甚至超过99.99%，且随着系统的复杂性增强，模拟流态故障率达到置信区间所需迭代次数逐渐减少，模拟时间亦得到了良好改善。

最后，通过FLUENT仿真后处理，各节点系统的速度矢量分布如图5所示。

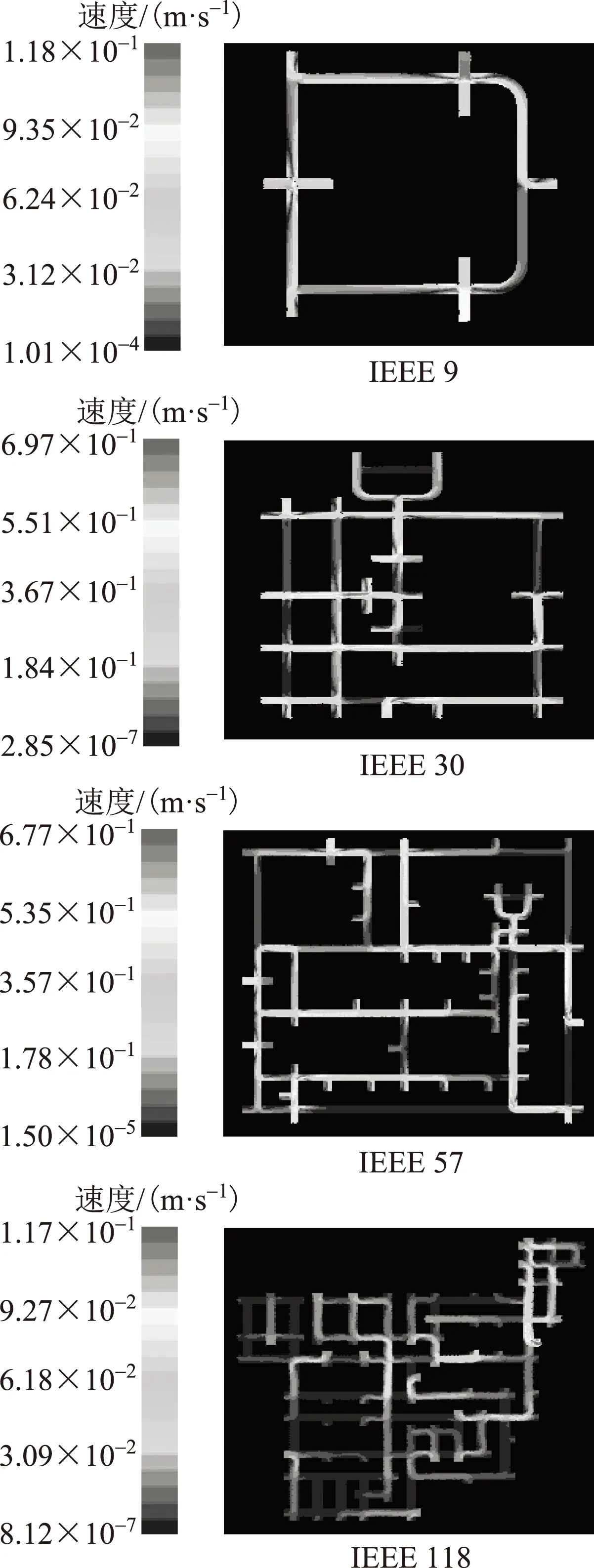
图5 各节点系统的速度矢量分布

通过分析可知：流态故障率在主变压器附近、线路大弧垂摆动波动较大的区域中频发率较高，需加强线路巡视，及时处理线路缺陷，提高供电可靠性；同时，通过分析各节点系统的速度矢量，由此获得各节点处流态故障率的等效流动体的速度值，再结合各节点处的综合健康指数加以修正，由式(20)求解出相应预测点处的流态故障率，预测结果见表3所示。

表3 各节点系统的流态故障率估算值

节点各节点系统故障率/%IEEE9IEEE30IEEE57IEEE11811.312.141.791.6521.072.031.311.5630.761.152.193.0142.212.152.942.6051.081.882.171.7761.142.261.492.0672.151.552.281.4481.962.853.091.7992.383.032.752.10102.552.192.411.51

此外，对IEEE 118节点系统采用组合预测法预测其故障率，以其实际故障率为参照数据，具体预估结果见表4，可知：使用组合预测模型预估架空输电线路故障率时，其预测结果的可靠性较本文所提出的CFD预测模型要低，相对误差也较高，故随着电网规模的逐渐扩大，有些输电线路故障率的常规预测方法亦显现出一定的弊端，降低了预测结果的可信度，影响判断线路发生故障的准确性，从而不能有效地预防及控制该故障。

表4 不同预测模型中的故障率估算值比较 %

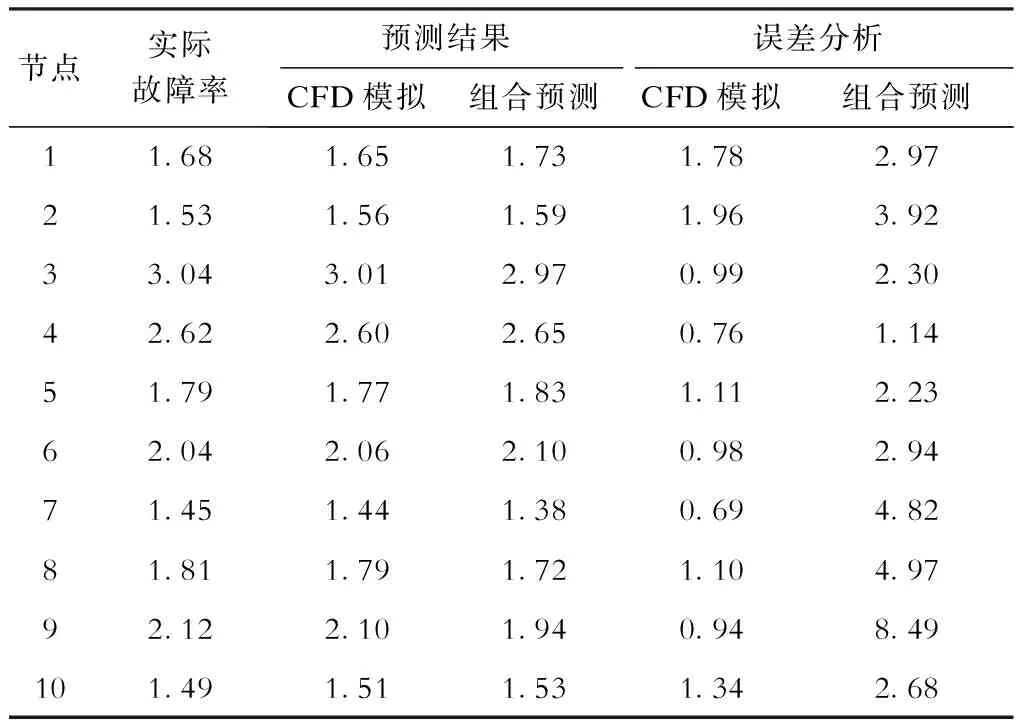
节点实际故障率预测结果CFD模拟组合预测误差分析CFD模拟组合预测11.681.651.731.782.9721.531.561.591.963.9233.043.012.970.992.3042.622.602.650.761.1451.791.771.831.112.2362.042.062.100.982.9471.451.441.380.694.8281.811.791.721.104.9792.122.101.940.948.49101.491.511.531.342.68

5 结论

本文在已知整个电力系统故障率的条件下，采用综合健康指数削弱各影响因素对线路故障率分布的波动作用，基于数值模拟和FLUENT软件相结合的方法模拟架空输电线路流态故障率的流场分布，模拟结果表明：

a) CFD仿真计算速度快，其预测结果可靠度高，方便人们作出准确的故障判断，及时采取有效的预防和维修措施；

b) CFD仿真的应用范围广，适用于估算复杂约束下的电力系统或其输电线路各节点处的故障率，且随着系统的复杂性增强，其预算结果的准确率越高；

c) CFD仿真可作为一种新的、有效的故障率预测工具适应网域范围日渐扩大的电力系统，其预测结果较其他常用方法优异，克服了传统预测模型及方法的多种弊端，可用其来预测架空输电线路中各线路段上发生故障的概率。

[1] 叶练方，王星华，颜少伟，等．基于马尔可夫模型的输电线路可靠性评估[J]. 广东电力，2015，28(1)：76-81. YE Lianfang，WANG Xinghua，YAN Shaowei，et al. Reliability Evaluation on Power Transmission Lines Based on Markov Model[J].Guangdong Eletric Power，2015，28(1)：76-81.[2] 李文沅．电力系统风险评估：模型、方法和应用[M].北京：科学出版社，2006.

[3] BO Z Q，AGGARWAL R K，JHONS A T，et al. A New Approach to Phase Selection Using Fault Generated High Frequency Noise and Neural Networks[J].IEEE Trans. on Power Delivery，1997，12(1)：106-115.

[4] 代晓光，杨振伟，谢平，等．输电线路鸟害防治对策[J]. 广东电力，2011，24(6)：47-49.

DAI Xiaoguang，YANG Zhenwei，XIE Ping，et al. Prevention Strategy for Bird Injury on Transmission Lines[J].Guangdong Eletric Power，2011，24(6)：47-49.

[5] BLACKETT G，SAVORY E，TOY N，et al. An Evaluation of The Environmental Burdens of Present and Alternative Materials Used for Electricity Transmission[J].Building and Environment，2008，43(7)：1326-1338.

[6] 文波，刘贞毅，洪彬倬．天气因素对配电网可靠性影响的探讨[J]. 广东电力，2012，25(9)：72-75.

WEN Bo，LIU Zhenyi，HONG Binzhuo. Discussion on Impact of Distribution Networks[J].Guangdong Eletric Power，2012，25(9)：72-75.

[7] 李瀚儒，张成巍．架空输电线路防雷评估新方法分析[J]. 广东电力，2015，28(5)：109-113.

LI Hanru，ZHANG Chengwei. Analysis on New Method for Evaluation on Lightning Protection of Overhead Power Transmission Lines[J].Guangdong Eletric Power，2015，28(5)：109-113.

[8] 李新民，朱宽军，李军辉．输电线路舞动分析及防治方法研究进展[J]. 高电压技术，2011，37(2)：484-490.

LI Xinmin，ZHU Kuanjun，LI Junhui. Review on Analysis and Prevention Measures of Galloping for Transmission Line[J].High Voltage Engineering，2011，37(2)：484-490.

[9] 周华敏，全玉生，房林杰，等．高压架空输电线路覆冰诊断新方法[J]. 广东电力，2015，28(11)：103-109.

ZHOU Huamin，QUAN Yusheng，FANG Linjie，et al. New Method for Icing Detection of HV Overhead Transmission Lines[J].Guangdong Eletric Power，2015，28(11)：103-109.

[10] 陈金熠，范春菊，胡天强，等．考虑架空输电线路状态的线路覆冰监测系统的研究[J]. 电力系统保护与控制，2012，40(15)：93-98.

CHEN Jinyi，FAN Chunju，HU Tianqiang，et al. Study on Monitoring System of Transmission Line Icing Considering the State of Overhead Transmission Lines[J].Power System Protection and Control，2012，40(15)：93-98.

[11] 孙羽，王秀丽，王建学，等．架空线路冰风荷载风险建模及模糊预测[J]. 中国电机工程学报，2011，31(7)：21-28.

SUN Yu，WANG Xiuli，WANG Jianxue，et al. Wind and Ice Loading Risk Model and Fuzzy Forecast for Overhead Transmission Lines[J].Proceeding of the CSEE，2011，31(7)：21-28.

[12] 刘益智. 不确定性CFD模拟方法及其应用研究[D]. 北京：华北电力大学，2014.

[13] 李莉，刘永前，杨勇平，等．基于CFD流场预计算的短期风速预测方法[J]. 中国电机工程学报，2013，33(7)：27-32. LI Li，LIU Yongqian，YANG Yongping，et al. Short-term Wind Speed Forecasting Based on CFD Pre-calculated Flow Fields[J].Proceeding of the CSEE，2013，33(7)：27-32.[14] 张雨浓，李巍，蔡炳煌，等．切比雪夫正交基神经网络的权值直接确定法[J]. 计算机仿真，2009，26(1)：157-161.

ZHANG Yunong，LI Wei，CAI Binghuang，et al. A Chebyshev Orthogonal Basis Neural Network with Direct Weight Determination[J].Computer Simulation，2009，26(1)：157-161.

[15] PATANKER S. Numerical Heat Transfer and Fluid Flow[M]. Washington Taylor & Francis，1980.

(编辑 王朋)

Assessment Method for Failure Probability of Overhead Transmission Lines Based on Computational Fluid Dynamics

XU Zhiqiang, WU Jiekang

(School of Automation, Guangdong University of Technology, Guangzhou, Guangdong 510006, China)

In allusion to influence on safe and stable operation of overhead transmission lines by lightning, wind speed, icing, flashover, bird touch, line dancing, aging, and so on, this paper discusses failure rate forecasting model for overhead transmission lines. It firstly fluidizes failure rate of overhead transmission lines and considers influence of various uncertain factors, then conducts weighted optimization on related influencing factors so as to solve for comprehensive health index. Meanwhile, it modifies fluid failure probability distribution of transmission lines for establishing a forecasting model for failure rate of overhead transmission lines affected by various factors. Finite volume method (FVM) is used for meshing for this model as well as computational fluid dynamics (CFD) principle is applied for simulation calculation, and predicted values with high accuracy are finally assessed according to results obtained. By taking IEEE 9, IEEE 30, IEEE 57 and IEEE 118 systems for calculation and analysis, it expounds that this model can effectively improve failure rate forecasting precision, and proves feasibility of CFD simulation in solving the problem of failure rate of overhead transmission lines.

overhead transmission line; fluid failure rate; comprehensive heath index; finite volume method (FVM); computational fluid dynamics(CFD)

2016-04-15

2016-08-03

国家自然科学基金(50767001)；广东省自然科学基金(2014A030313509)；中国南方电网有限责任公司科技项目(K-GD2014-194)

10.3969/j.issn.1007-290X.2016.10.019

TM75

A

1007-290X(2016)10-0109-07

胥志强(1990)，男，江西丰城人。在读硕士研究生，主要研究方向为电力系统运行与控制。

吴杰康(1965)，男，广西隆安人。教授，工学博士，主要研究方向为电力系统运行与控制。