±800 kV换流变压器阀侧电容式直流套管电场分析

祝贺,姜宰东

(东北电力大学 建筑工程学院，吉林 吉林132012)



±800 kV换流变压器阀侧电容式直流套管电场分析

祝贺,姜宰东

(东北电力大学 建筑工程学院，吉林 吉林132012)

为研究特高压直流套管的绝缘性能，建立了±800 kV复合电容式套管有限元模型，用ANSOFT分析软件对内采用绝缘环氧树脂绝缘纸和外绝缘采用高温硫化硅橡胶外套制造的复合电容式套管进行二维电场分析，获得特高压直流套管内部精确场强分布和电位分布。该结果表明：套管内部环氧树脂中的屏障强迫了电位分布，使法兰附近的电场分布均匀，却造成法兰顶端等位线发生剧烈变化，径向电位梯度大；法兰部分与高温硫化硅橡胶伞裙的接连处电场强度最大，最大值达3.44 MV/m，在特高压直流运行时最易产生闪络,是必须注意的问题。

直流套管；有限元分析；电场强度；电容芯子；电位分布

高压直流套管是直流输电设备的重要高端设备，其安全可靠性对于直流系统的安全稳定运行有着重要的意义[1-2]。近年来，随着高压直流输电在全国电网中比例的增加，高压直流设备在电力系统中的重要性越来越明显。在高电压作用下,绝缘介质形成很高的场强，常被电击穿[3]，电气设备绝缘性能破坏[4-6]，导致特高压直流工程中采用的特高压直流套管仍然需要国外进口。由此可见，计算绝缘结构中可能出现的最高场强、分析发生绝缘破坏的根本原因，对特高压直流套管的制造与设计具有重要意义[7-9]。

特高压直流套管不但承受直流、交流电以及套管本身芯子内部均压极板外，还要承受极板外侧绝缘层的影响[10-14]。由于电导率随温度变化而变化，特高压直流套管的电场分布更加复杂[15-16]，容易产生绝缘破坏等问题。为了解决特高压直流套管绝缘问题，有必要对套管进行电场分布分析[17]。为此，基于麦克斯韦电磁场理论以及麦克斯韦方程组，建立复合式高压绝缘套管电场的数学分析模型，考虑电导率和介电常数对电场分布的影响，并运用ANSOFT软件对套管内部及电容芯子的电场分布进行详细的数据分析，以此来提高绝缘套管的可靠性及可行性。

1 直流套管电场分析理论基础

1.1 电场分析数学模型

特高压套管为严格的轴对称结构，其模型求解可归结为二维轴对称静电场边值问题，利用麦克斯韦方程组的微分形式来描述准静态场中的电场方程,即

(1)

(2)

(3)

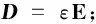
(4)

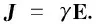
(5)

式中：ε为相对介电常数，F/m；γ为电导率，S/m。当介质电导率γ和相对介电常数ε都是常数时，介质为线性介质。

由式(1)至(5)可以看出，介质存在自由电荷引起的传导电流和位移电流，电场分布由介电常数和电阻率同时决定。

由电磁场基本理论可知，电介质在交流电压激励下，介质中的传导电流很小，与位移电流相比可以忽略不计，所以交流电压激励下介质内部的场强可以认为只与介电常数有关，材料的电阻率对电场分布的影响可以忽略不计。在直流电压作用下，套管场域为电流传导场，介质内部场强分布只与电阻率有关。

静电场域中电位与电场的关系为

(6)

式中φ为整个场域中的电网函数。

由式(1)至(6)得到电准静态场中的电位方程描述为

(7)

传导电流、电介质对场域中电位分布的影响可用于求解任何场源激励下电介质中的线性电场电位分布。

1.2 电场计算的边界条件及电场特点

1.2.1 电场计算的边界条件

电磁场理论中，电场具有三类边界条件[18]，本文采用第一类狄利克莱(Dirichlet)边界条件，即已知边界条件上的电位值为

(8)

第二类边界条件在有限元计算时会自动满足变分条件；第三类为混合边界条件，即第一类边界和第二类边界的线性组合，在高压电器分析中不存在第三类边界条件，所以实际计算时，只需要定义第一类边界条件。

1.2.2 高长径比场域

套管为细长结构，特高压套管长径比更大，对该结构所建立的电场分析区域称之为高长径比场域。

1.2.3 边界等效处理

电场分析的区域为无限空间，用ANSOFT远场边界来近似等效无限远空间，边界等效的处理对精确的电场分析起到关键作用。

2 特高压直流套管电场分析

2.1 特高压套管电场分析仿真模型建立

本文研究的±800kV换流变压器套管用于直流系统中环流变压器阀侧出线及其绝缘，套管内部采用环氧树脂内绝缘的同时充入一定压力的SF6气体，外绝缘采用高温硫化硅橡胶伞裙作为保护。由于套管顶部出线装置结构复杂，设计了均压罩保护，在套管内部SF6气体中设计均压罩避免气体放电，为防止电场局部集中，在环氧树脂中设置铝箔内屏蔽，环氧树脂内屏与导杆相连，末屏连接法兰。具体结构如图1所示。

图1 特高压直流套管2D电场计算模型

±800 kV复合电容式特高压直流套管由环氧树脂内绝缘、高温硫化硅橡胶伞裙外绝缘、内部充入气体、中心导杆以及金属连接构件所组成，所用材料的计算参数见表1。

表1 材料的计算参数

材料名称相对介电常数电导率/(S·m-1)铜20001.75×108环氧树脂3.93.9×10-12硫化硅橡胶4.51×10-12变压器油2.22×10-13SF61.0021×1020

2.2 特高压直流套管网格划分

变压器套管为细长结构，绝缘结构复杂，虽然对模型做了适当简化，但是小尺寸结构部位依然很多，经过大量修改，运用单元尺寸与线段网格控制等多种网格控制手段，并对网格局部细化，得到全部模型网格剖分总个数47 562，最大和最小尺寸相差近15倍，局部网格细节如图2所示。

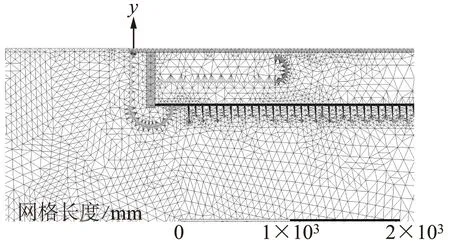
图2 顶部屏蔽罩网格划分

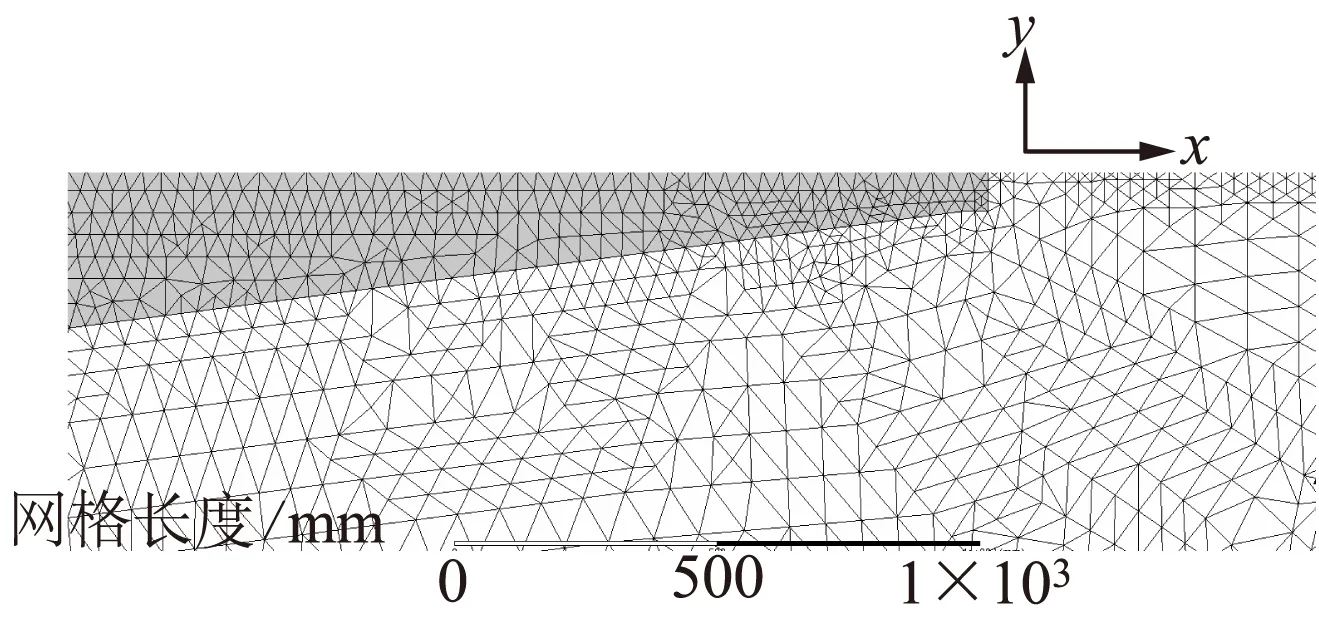
图3 变压器油网格划分

根据GB/T 22674—2008《直流系统用套管》规定，换流变压器套管需要进行直流耐压试验，激励电压值

(9)

式中： Udc为直流耐受试验电压值；N为连接从直流导线中性点与换流变套管整流桥的一系列六脉动桥数；Udc,m为每个阀桥的最高直流电压；Uac,m为安装套管的换流变压器阀绕组的最大交流运行线电压。直流套管的试验电压幅值是与其相连换流变压器试验数值的1.15倍，根据文献《特高压直流电气设备》中的试验电压数值，得到Udc=960kV。

3 直流套管电场分析结果

3.1 电位分布

中心导杆施加的直流耐压试验值为960kV，接地法兰施加电压为0kV,环氧树脂内屏与导杆相连为高电位，末屏与法兰相连为零电位，根据施加的边界条件，计算的电位分布如4图所示。

图4 特高压直流套管电位分布

由图4可知，由于环氧树脂中的屏障强迫了电位分布，法兰附近的电场分布均匀，但是法兰两部顶端等位线发生剧烈变化，径向电位梯度大。变压器油、顶部均压罩、套管内部均压装置和SF6气体保护了套管内部结构，外侧等位线较密集。

由于介质电气特性不同，在介质交界面会造成交界面两侧电场强度不同。由电位分布局部图可以看出，特高压直流套管的绝缘芯子起到了很好的降低电压的作用，从中心导杆到法兰，特高压直流套管电位在0.425 m的距离内从高电位降至零电位，法兰附近的环氧树脂电场强度较大，电场分布不均匀，特高压直流套管顶部电位分布与电容芯子处的电分布如图5、图6所示。

图5 特高压直流套管顶部电位分布

图6 特高压直流套管电容芯子电位分布

由电位分布的细节图5、图6可以观察到，等位线在套管内部的交界面处易发生变化，在直流电场分析中，为两种介质电导率的反比。设特高压直流套管中各层极板为悬浮电位，计算得到特高压直流套管各层极板上的电位如图7所示。

从图7可知，在直流电压作用下，层极板与导杆相连，电位最高为960 kV,最外层极板与法兰相连电位为0 kV，由于内绝缘环氧树脂的电导率低，所以直流电压作用下的大部分电压主要作用在各层级板上。

3.2 电场强度分布

计算特高压直流套管中电场强度后，到了特高压套管接地法兰附近的最大场强分布如图8所示。

从图8可看到，法兰表面电场强度云图层次分明,法兰与套管伞裙的交接处电场强度最大 ,最大场强为3.44 MV/m，并且沿伞群方向逐渐降低，电场分布不均，此处最容易发生绝缘问题。

如图9所示，当法兰与伞裙连接后，表面场强迅速下降，距离法兰1 m处电场强度下降0.46 MV/m。在直流电压作用下，在绝缘介质交界面处容易发生电场强度的畸变，此处是薄弱环节，最易发生闪络，在设计制造时应注意绝缘问题发生。

图9 法兰处电场强度分布曲线

顶部均压罩下端与绝缘外套相接处电场强度如图10所示，套管场强最大值位于顶部均压罩与伞裙相接处，最大值为0.4 MV/m,且沿着伞裙方向场强逐渐减小。

图10 均压罩下端场强分布

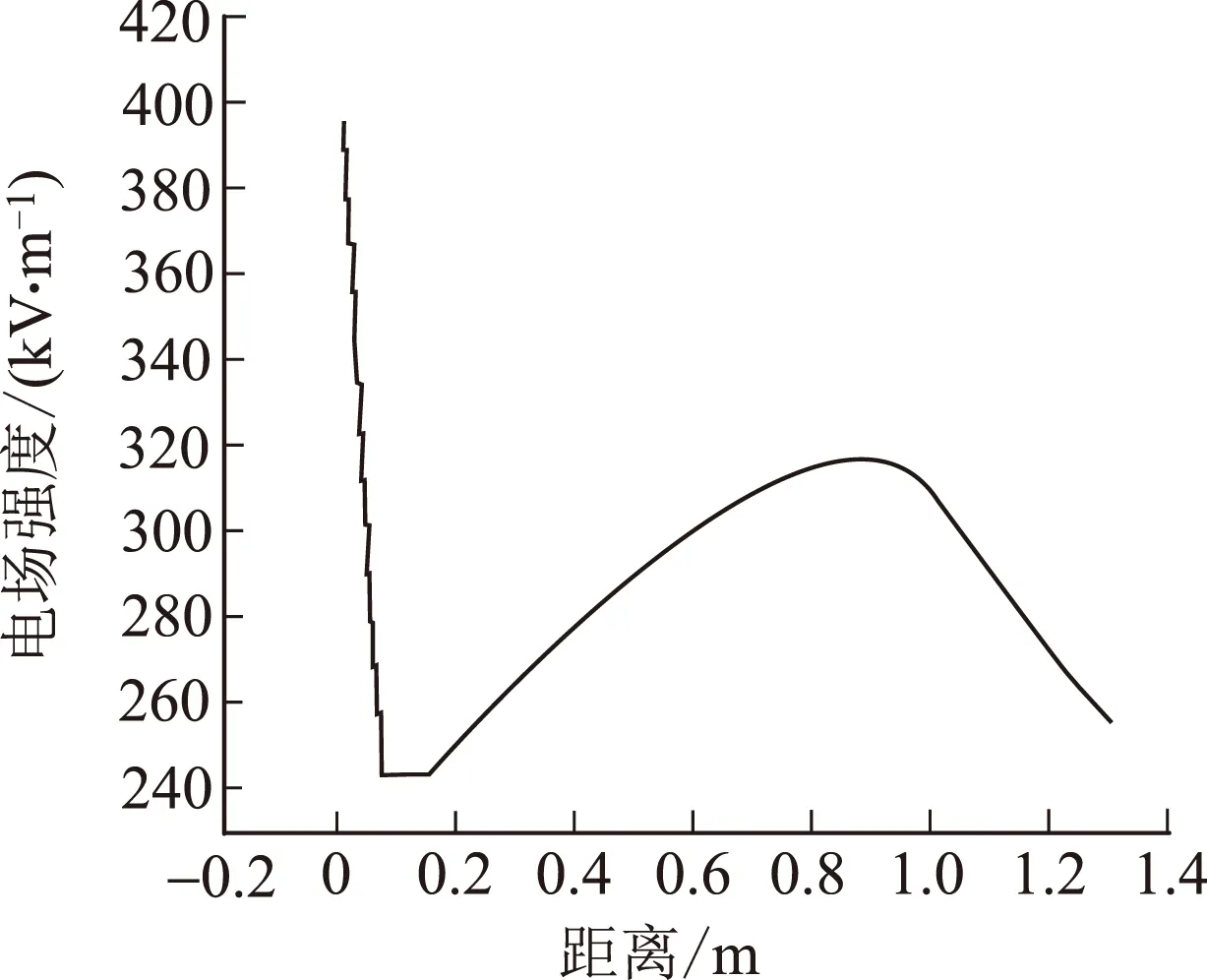
图11 均压罩下端场强分布曲线

从计算结果可知，在高压套管顶部均压罩与绝缘外套相接处电场强度易发生突变，但此处的电场强度值最大值为0.40 MV/m，远小于空气的击穿场强，套管绝缘外套表面场强最大值发生在伞裙与法兰相接处，该处电场值最高可达到3.44 MV/m,是套管表面场强的薄弱点，在此处易发生闪络等绝缘破坏，所以在设计和制造时应注意此类问题的发生。

4 结束语

a) 本文采用±800 kV复合电容式直流套管作为研究对象，内绝缘采用环氧树脂的同时充入SF6气体作为保护，在考虑多种绝缘材料的电导率情况下对特高压直流套管进行电场分析，在直流场中，介质交界面两侧场强与材料电导率为反比关系。

b) 复合电容式特高压直流套管中的法兰部分与高温硫化硅橡胶伞裙的接连处电场强度最大，此处最容易发生闪络，最大场强值可达到 3.44 MV/m， 在设计制造时应注意此类绝缘问题的发生。

c) 特高压直流套管顶部电场分布不均匀，易发生电场突变，特高压套管顶部的均压罩可有效降低出线端最大场强，增大了套管发生绝缘破坏的安全裕度。

d) 复合电容式套管内部环氧树脂中的屏障强迫了电位分布，使电容芯子内部电场分布均匀，但是屏障两端的等位线变化幅度较高，电容芯子径向电位梯度较大。

[1] 董淑建,何平.油纸电容式套管的发展与展望[J].电瓷避雷器, 2005, 207(5):5-11.

DONG Shujian, HE Ping. Development and Prospect of Greaseproof Paper Condenser Bushing [J].Insulators and Surge Arresters, 2005, 207(5):5-11.

[2] 张书琴, 张克选, 高延峰, 等. 交流550 kV高压套管的绝缘设计研究[J].高压电器，2015，51(2):105-115.

ZHANG Shuqin, ZHANG Kexuan, GAO Yanfeng, et al. AC 550 kV High Voltage Insulation Sleeve Study Design [J]. High Voltage Electrical Apparatus, 2015, 51 (2):105-115.

[3] 罗隆福, 李建州, 孙红梅.高压直流穿墙套管非线性电场的求解[J].高电压技术，2002, 28(5): 3-5.

LUO Longfu, LI Jianzhou, SUN Hongmei. HVDC Wall Bushing for Solving Nonlinear Electric Field [J]. High Voltage Engineering, 2002, 28 (5): 3-5.

[4] 江汛,王仲奕.复合高压套管的电场计算与分析[J].高电压技术, 2004, 30(3):17-21.

JIANG Xun, WANG Zhongyi. Calculation of Electric Field and Analysis of Complex High Voltage Bushing [J]. High Voltage Engineering, 2004, 30(3): 17-21.

[5] 周晔, 魏俊梅.1 100 kV硅橡胶套管绝缘结构优化设计[J].电器制造, 2010(10):72-74.

ZHOU Ye, WEI Junmei.1 100 kV Insulation Silicone Rubber Casing Structure Optimization[J].Electrical Manufacturing, 2010(10):72-74.

[6] OKUBO H, NARA T, SAITO H. et al. Discharge Mechanism at HVDC Polarity Reversal in Oil/Pressboard Composite Insulation System[C]//IEEE International Conference on Dielectric Liquids. Trondheim, Norseland: IEEE , 2011:16-25.

[7] 金立军,郭裕,薛义飞, 等.高压绝缘套管电场分析及结构优化[J].高压电器，2015，51(4):7-12.

JIN Lijun, GUO Yu, XUE Yifei, et al. High Voltage Electric Field Analysis and Structure Optimization [J] .High Voltage Electrical Apparatus, 2015, 51 (4): 7-12.

[8] 杜清全, 蔡钢, 黄晓峰, 等.极性反转下特高压换流变阀侧套管电场分析[J].电磁避雷器，2013，253(3)：14-18.

DU Qingquan,CAI Gang, HUANG Xiaofeng, et al. Polarity Reversal Under UHV Converter Side Bushing Electric Field Analysis[J].Electric Porcelain Arrester, 2013, 253 (3): 14-18.

[9] SMITH D J, MCMEEKIN S G, STEWART B G .The Modelling of Electric Field, Capacitance and Dissipation Factor of a High Voltage Bushing over Varying Frequency[C]// 2010 45th International Conference on Universities Power Engineering. [S.l.]:IEEE , 2010:1-6.

[10] 张施令, 彭宗仁, 刘鹏. 特高压干式油气套管内绝缘结构的优化设计[J].西安交通大学学报, 2014, 48(8):116-121.

ZHANG Shiling, PENG Zongren, LIU Peng. Optimization of Oil and Gas Within the UHV Dry Sleeve Insulation Structure Design[J]. Journal of Xi’an Jaotong University, 2014, 48(8):116-121.

[11] PARIS O, LEWINER J. A Finite Element Method for the Determination of Space Charge Distributions in Complex Geometry [J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2000, 7(4):556-560.

[12] 许佐明, 胡伟. 550 kV环氧浸渍干式油-电容套管温度场分析[J].高电压技术，2012，38(11)：3087-3092.

XU Zuoming, HU Wei. 550 kV Epoxy Impregnated Dry Oilcapacitor Bushing Temperature Field Analysis [J]. High Voltage Engineering, 2012, 38 (11): 3087-3092.

[13] MONTANARI G C FABIANI D. Evaluation of DC Insulation Performance Based on Space Charge Measurements and Accelerated Life Tests[J].IEEE Trans. on Dielectrics and Electrical Insulation , 2000 , 7(3):322-328 .

[14] 许学勤, 张重远, 李燕青,等. 接地内屏蔽对SF6套管电场分布影响的研究[J].华北电力大学学报(自然科学版)，2007，34(6)：11-14.

XU Xueqin, ZHANG Zhongyuan, LI Yanqing, et al. A Grounded Shield Casing Electric Field Distribution on SF6Research[J]. Journal of North China Electric Power University (Natural Science Eedition), 2007,34 (6): 11-14.[15] 申积良, 黄福勇, 周卫华, 等.高压变压器油/气套管现场介质损耗试验方法讨论[J].高压电器，2009, 45(4):71-73.

SHEN Jiliang, HUANG Fuyong, ZHOU Weihua, et al. High Voltage Transformer Oil / Gas Field Casing Dielectric Loss Test Methods Discussed [J]. High Voltage Electrical Apparatus, 2009, 45 (4): 71-73.

[16] 刘鹏, 金海云, 石惠承, 等. 特高压直流套管用环氧树脂/皱纹纸复合绝缘体系介电性能的研究[J].高压电器, 2009，45(5): 6-8.

LIU Peng, JIN Haiyun, SHI Huicheng, et al. Epoxy Resin / Crepe Paper Composite Insulation System Dielectric Properties[J]. High Voltage Electrical Apparatus, 2009, 45(5); 6-8.

[17] 张国强，张元录. 高压套管均压球电极形状优化的研究[J].中国电机工程学报,1999,19(11): 37-40.

ZHANG Guoqiang, ZHANG Yuanlu. Research on High Voltage Bushing Equalizing Ball Electrode Shape Optimization [J]. Proceedings of the CSEE, 1999, 19(11): 37-40.

[18] 张施令，彭宗仁，刘鹏, 等. 电热耦合模型应用于高压干式直流套管径向温度和电场分布计算[J]. 中国电机工程学报, 2013, 33(22)：191-200.

ZHANG Shiling, PENG Zongren, LIU Peng, et al. Electric Coupling Model is Applied to High Voltage DC Dry Casing Temperature and Radial Electric Field Distribution Calculation [J]. Proceedings of the CSEE, 2013,33 (22): 191-200.

(编辑 王夏慧)

Electric Field of Capacitive DC Bushing at ±800 kV Converter Transformer Valve Side

ZHU He, JIANG Zaidong

(Institute of Civil Engineering, Northeast Dianli University, Jilin, Jilin 132012, China)

In order to study insulation performance of ultra-high voltage DC bushing, this paper establishes a finite element model for ±800 kV composite capacitor bushing and uses ANSOFT analysis software for 2D electric field analysis on the composite capacitor bushing which uses epoxy resin insulation paper for internal insulation and high-temperature vulcanizing silicone rubber coat for external insulation. It obtains precise electric field strength distribution and potential distribution inside the ultra-high voltage DC bushing. Results indicate the epoxy resin barrier inside the bushing forces potential distribution that not only causes homogeneous distribution of electric field near the flange but also make equipotential lines on the top of flange change greatly and gradient of radial potential large. It also discovers electric field at the joint of flange and high-temperature vulcanizing silicone rubber umbrella skirt is the most intensive and the maximum value is 3.44 MV/m. In addition, it points out to pay attention to one problem of flashover at the moment of ultra-high voltage DC operation.

DC bushing; finite element analysis; electric field strength; capacitor core; potential distribution

2016-06-26

吉林省教育厅“十二五”科学技术研究项目(2015252).吉林市科技创新发展计划项目(201464058)

10.3969/j.issn.1007-290X.2016.10.017

TM85

A

1007-290X(2016)10-0097-05

祝贺(1978)，男，黑龙江讷河人。教授，硕士生导师，工学博士，研究方向为电网运行设备检测及故障修复新技术。

姜宰东(1991)，男，吉林德惠人。在读硕士研究生，研究方向为输电工程特高压绝缘。