基于LMD和阶次跟踪分析的滚动轴承故障诊断*

2016-11-23程军圣

振动、测试与诊断 2016年3期

关键词：阶次内圈外圈

张亢, 程军圣

(1.长沙理工大学能源与动力工程学院长沙,410114)(2.湖南大学汽车车身先进设计制造国家重点实验室长沙,410082)

基于LMD和阶次跟踪分析的滚动轴承故障诊断*

张亢1, 程军圣2

(1.长沙理工大学能源与动力工程学院长沙,410114)(2.湖南大学汽车车身先进设计制造国家重点实验室长沙,410082)

变转速工况下的滚动轴承故障振动信号具有多分量调制以及故障特征频率受到转频调制的特点，从而导致故障特征提取困难。对此，将局部均值分解(local mean decomposition，简称LMD)与阶次跟踪分析相结合，提出了一种变转速工况下的滚动轴承故障诊断方法。首先,采用阶次跟踪采样将时域滚动轴承故障振动信号转换到角域;然后，对角域信号进行LMD分解得到若干个乘积函数(product function，简称PF)分量;最后，对各个PF分量的瞬时幅值进行频谱分析,判断滚动轴承的故障部位和类型。通过对滚动轴承实验故障振动信号的分析，结果表明该方法能有效地应用于变转速工况下的滚动轴承故障诊断。

滚动轴承；故障诊断；解调；局部均值分解；阶次跟踪

引言

滚动轴承作为一种旋转机械部件，其变转速过程的振动信号往往包含了丰富的状态信息，一些在平稳运行时不易体现的故障特征可能会充分地表现出来[1]。因此，对滚动轴承变转速过程的振动信号进行分析对于滚动轴承的故障诊断非常有意义。然而，此时其振动信号往往是非平稳的，并且与轴转速密切相关，表现出随轴转速变化的调频特征，直接进行频谱分析，通常会发生“频率混淆”现象[2]，无法提取出与转速有关的故障信息。阶次跟踪分析是指通过跟踪参考轴的转速来实现等角度增量采样，将时域非平稳信号转换到角域平稳信号的过程，其能够提取振动信号中与转速有关的信息，同时对与转速无关的信号进行抑制[3]。因此，阶次跟踪分析非常适合于处理变转速工况下的滚动轴承振动信号。另一方面，当滚动轴承发生故障时，其振动信号为多分量的调幅-调频信号[4]，在进行解调分析之前还需要将其分解为若干个单分量的调幅-调频信号，在目前的非平稳信号分解方法中，常用的有经验模态分解(empirical mode decomposition，简称EMD)[5]和小波分解。EMD可以对多分量信号进行自适应分解，但其理论上还存在一些问题，如模态混淆[6-7]、过包络、欠包络[8]和端点效应[9-10]等。小波分解的理论和应用都比较成熟，但其最大缺陷就是缺乏自适应性，这表现在分解时采用的是固定的小波基函数和分解尺度[11]。局部均值分解(local mean decomposition，简称LMD)[12]是一种新的非平稳信号分析方法，能够将一个多分量信号自适应地分解为若干个瞬时频率具有物理意义的乘积函数分量之和，其中每一个PF分量由一个包络信号和一个纯调频信号相乘而得到，包络信号就是该PF分量的瞬时幅值，瞬时频率则可由纯调频信号直接求出。因此，整个LMD的分解过程就是一个完整的解调过程，非常适合于处理滚动轴承故障振动信号。笔者将LMD与阶次跟踪分析相结合应用于变转速工况下滚动轴承的故障诊断。对滚动轴承不同部位故障的试验数据进行了分析，结果表明该方法可以有效地应用于变转速工况下滚动轴承的故障诊断。

1 计算阶次跟踪法

阶次跟踪采样是指参照参考轴的转速对信号进行等角度重采样，其能够提取信号中与参考轴转速有关的信息，同时抑制与转速无关的信号，因此适合于分析变转速工况下的滚动轴承振动信号。目前，常用的阶次跟踪采样方法主要有硬件阶次跟踪法[13]、计算阶次跟踪法[14]和时频分析阶次跟踪法[15]等。其中计算阶次跟踪法(computed order tracking，简称COT)通过软件的形式实现等角度重采样，该方法的分析精度高，对被分析的信号没有特别的要求，并且无需特定的硬件，是一种应用广泛的阶次跟踪分析方法。COT法主要包括以下3个步骤。

1) 对振动信号和转速信号，分两路以恒定的采样率同时进行等时间间隔Δt采样，分别设为x(n)和s(n)。其中s(n)并不是直接表现为参考轴的瞬时转速，而是表现为频率随转速变化而变化的正弦电压信号，且s(n)中每一个过零点的时刻都对应着参考轴转过一周的时刻值。

2) 通过转速信号s(n)计算等角度增量Δθ所对应的时间序列tik。先搜索s(n)中满足条件s(n)≤0且s(n+1)≥0的点，并假设对应时刻值tsn和tsn+1之间的波形是线性的。因此，可由下式求得s(n)精确的过零点时刻值tzi，即参考轴每旋转一周所对应的时刻值

(1)

对时间序列tzi求差分即可得到参考轴每旋转一周所需的时间Ti。

根据文献[14]可以假设参考轴在旋转一周的时间内做的是匀变速运动，并假设前两周的角加速度是相等的。根据运动学定律，可以通过方程组(2)估计出前两周的初速度v10和角加速度a1为

(2)

设参考轴每转一周等角采样M个点，即等角度增量Δθ=2π/M。因此，第k个采样点对应参考轴转过的角度为2kπ/M，于是，可以由下式求出前两周中每个等角采样点所对应的时刻值tik、瞬时转速vik以及第3周的初速度v30

(3)

(4)

其中:角标i代表旋转的周数;角标k代表每转内的第k个采样点。

进一步可以由式(5)递推求出第i=3,4,…周的角加速度ai以及初速度vi+1,0

(5)

根据式(6)可以递推计算出第i=3,4,…周内的等角采样时刻tik和瞬时转速vik

(6)

3) 根据等角采样时刻值tik(i=1,2,…)，对振动信号x(n)进行插值(具体插值方法可自行选择)，求出振动信号在等角采样时刻值tik所对应的幅值，从而得到了振动信号的等角度重采样信号x(tik)。x(tik)是角域平稳信号，因此，可以对其进行传统的频谱分析。

上述COT法的基本原理是在旋转轴的每一个旋转周期进行M个点的等角度采样，通过改变点数M可以得到不同周期的转速采样，因此工程上常用的1/4周期转速采样实际为上述COT法的特例，说明了上述COT法相对于1/4周期转速采样更加灵活。但对于时域信号,不论是上述COT法还是1/4周期转速采样法都属于变频采样，变频采样的误差主要来自：a.对转速传感器得到的正弦电压信号过零点时刻值的计算；b.对旋转轴在旋转一周的周期内做匀变速运动的假设；c.对时域振动信号的插值。总的来说，每一个旋转周期的等角采样点数越多，分析误差越小，但对硬件的分析能力(如采样字长、采样频率等)要求也越高，反之亦然。以现在电子计算机的发展水平，以上误差一般较小，完全能满足工程实际的需求。

2 基于LMD和COT的滚动轴承故障诊断方法

2.1 诊断原理

当滚动轴承发生故障时，其振动信号具有多载波多调制的特性，是一种多分量的调幅-调频信号。包络解调是一种有效的提取故障特征的方法，但要进行包络解调分析，需要采用适当的信号分解方法，将信号中的各个分量进行分离，笔者拟采用LMD方法。LMD作为一种新的非平稳、非线性信号分析方法，能够将任意一个复杂信号自适应地分解为若干个PF分量之和，其中每一个PF分量代表了原信号的一种特征成分。与类似的EMD方法相比，LMD具有迭代次数少、端点效应不明显、瞬时频率无负频率等优点[16]，因此，LMD非常适合于对多分量的滚动轴承振动信号进行分解。LMD的具体分解步骤可参考文献[17]。基于LMD的阶次跟踪分析方法应用于变转速工况下的滚动轴承故障诊断，其步骤如下：

1) 采用COT法对滚动轴承振动信号进行等角度重采样，得到角域平稳信号；

2) 对角域平稳信号进行LMD分解，得到一系列PF分量，以及它们的瞬时幅值(即包络信号)；

3) 对包络信号进行频谱分析，得到包络阶次谱，从中分析滚动轴承的工作状态。

2.2 诊断实例

图1 旋转机械故障实验台Fig.1 Rotating machinery fault test rig

图2 故障的滚动轴承Fig.2 The roller bearing with defect

为了验证方法的可行性，在图1所示的旋转机械故障实验台上进行了滚动轴承外圈、内圈局部损伤以及正常3种工况的瞬态实验。实验用的滚动轴承型号为SKF6307，故障是通过激光切割在内圈或外圈上开轴向槽来设置的，槽的结构示意图如图2所示。理论计算的内圈和外圈故障特征阶次分别为xi=4.95和xo=3.04。图3是由振动传感器测得的内圈局部损伤的滚动轴承振动加速度信号s(t)，其中采样频率为8 192 Hz，采样时间为20 s。图4是将转速传感器测得的电压信号，按照第1节方法估计出的参考轴瞬时转速v(t)。从图4可以看出,输入轴经历了一个先加速再减速的过程，而图3中s(t)的幅值做出了相应的变化。不失一般性，截取图3中6～8 s加速过程的信号s1(t)进行分析。图5是直接对s1(t)进行频谱分析的结果，可以看出，由于转速是变化的，频谱图发生了“频率混淆”现象，难以反映系统的真实状态。采用本方法首先对s1(t)进行等角度重采样，设定每转一周等角度采样点数为200，即最大分析阶数为100，得到角域信号s1(θ)如图6所示，其中横坐标已由时间t变为了弧度θ。由于s1(θ)仍然为一个多分量的调幅-调频信号，受到调制与噪声的影响，故障特征信息难以分辨，需进一步处理。

图3 滚动轴承内圈故障振动信号Fig.3 The vibration signal of roller bearing with inner race defect

图4 轴瞬时转速Fig.4 Instantaneous speed of shaft

图5 内圈故障振动信号的频谱Fig.5 The spectrum of vibration signal with inner race defect

图6 阶次重采样后的内圈故障振动信号Fig.6 The vibration signal with inner race defect after order resampling

LMD是一种自适应信号分解方法，能将原信号的各种频率成分从高频到低频自适应地分离出来，然后只保留有意义的频率成分作下一步的分析。根据以上思想，进一步对s1(θ)进行LMD分解，得到了6个PF分量，以及各个PF分量的瞬时幅值(即包络信号)，这实际上就是s1(θ)的一个解调过程。经分析前两个PF分量PF1(θ)和PF2(θ)包含有故障特征信息(图7)，其他PF分量为转频以及噪声成分。因此，进一步对PF1(θ)和PF2(θ)的包络信号a1(θ)和a2(θ)进行频谱分析，结果分别如图8和图9所示。从图8可看出，在阶次为4.95和9.90处有清晰的谱线，分别对应着1,2倍内圈故障特征阶次xi和2xi，并且在xi和2xi处两边有以转频为间隔的调制边频带。图9中在阶次为1和4.95处有清晰的谱线，分别对应着转频阶次xr以及内圈故障特征阶次xi，这符合滚动轴承内圈故障机理，说明滚动轴承内圈发生了局部故障，验证了方法的有效性。

图7 图6所示信号的LMD分解结果Fig.7 The decomposition result of fig.6 shows signal by LMD

图8 图7中PF1(θ)的包络阶次谱Fig.8 The envelope order spectrum of the PF1(θ) in fig.7

图9 图7中PF2(θ)的包络阶次谱Fig.9 The envelope order spectrum of the PF2(θ) in fig.7

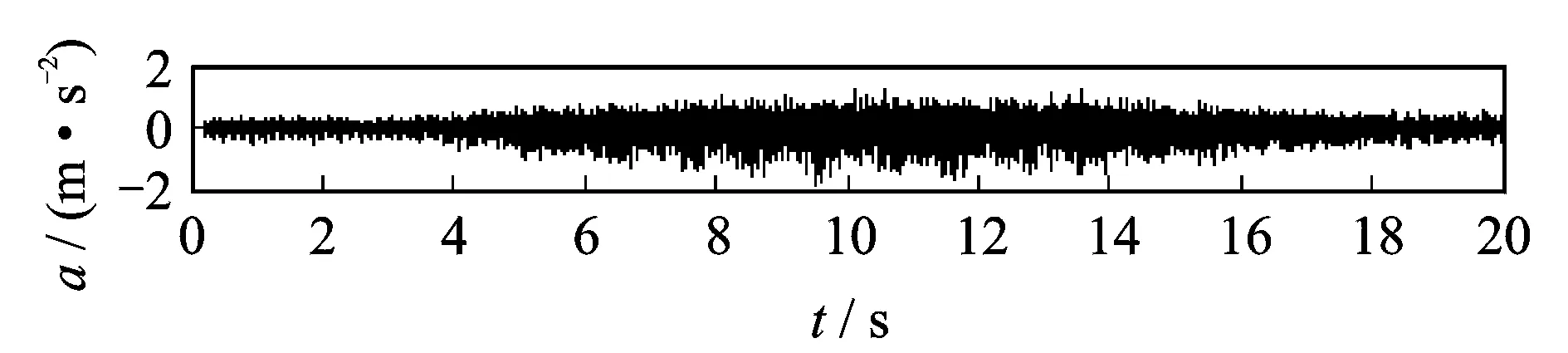
图10 滚动轴承外圈故障振动信号Fig.10 The vibration signal of roller bearing with outer race defect

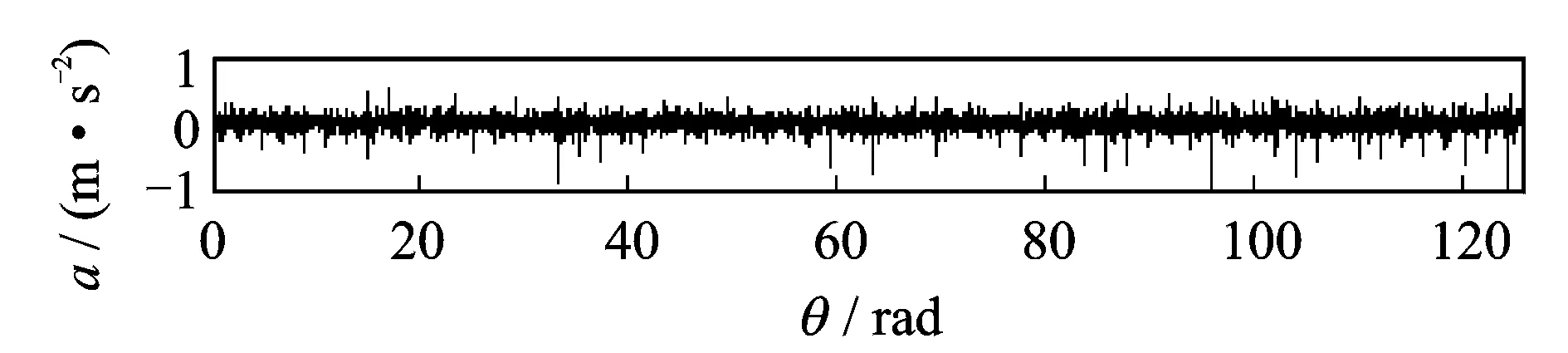
图11 阶次重采样后的外圈故障振动信号Fig.11 The vibration signal with outer race defect after order resampling

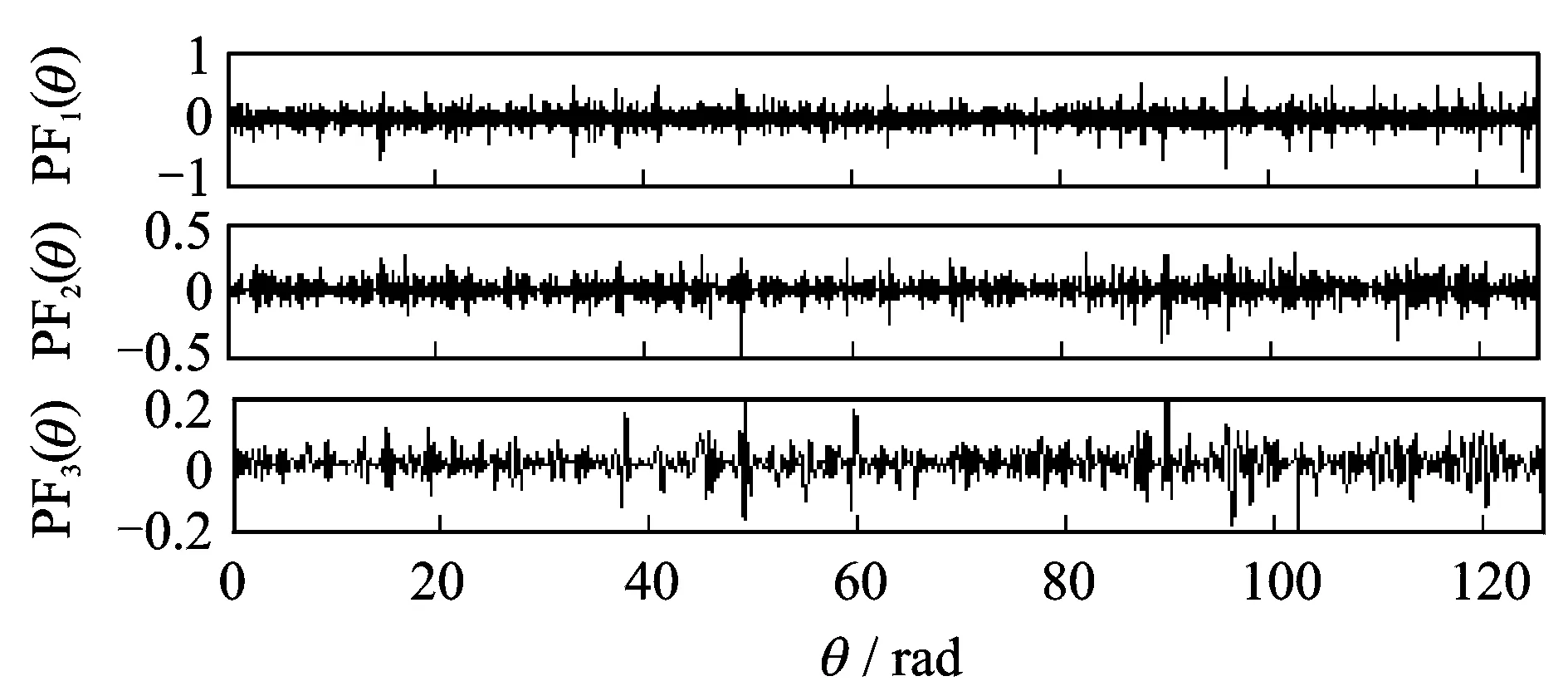
图12 图11所示信号的LMD分解结果Fig.12 The decomposition result of fig.11 shows signal by LMD

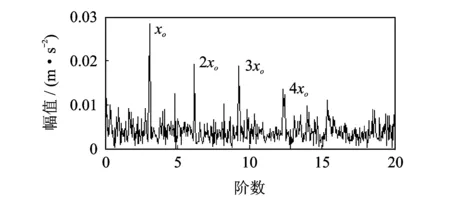
图13 图12中PF1(θ)的包络阶次谱Fig.13 The envelope order spectrum of the PF1(θ) in fig.12

图14 图12中PF2(θ)的包络阶次谱Fig.14 The envelope order spectrum of the PF2(θ) in fig.12

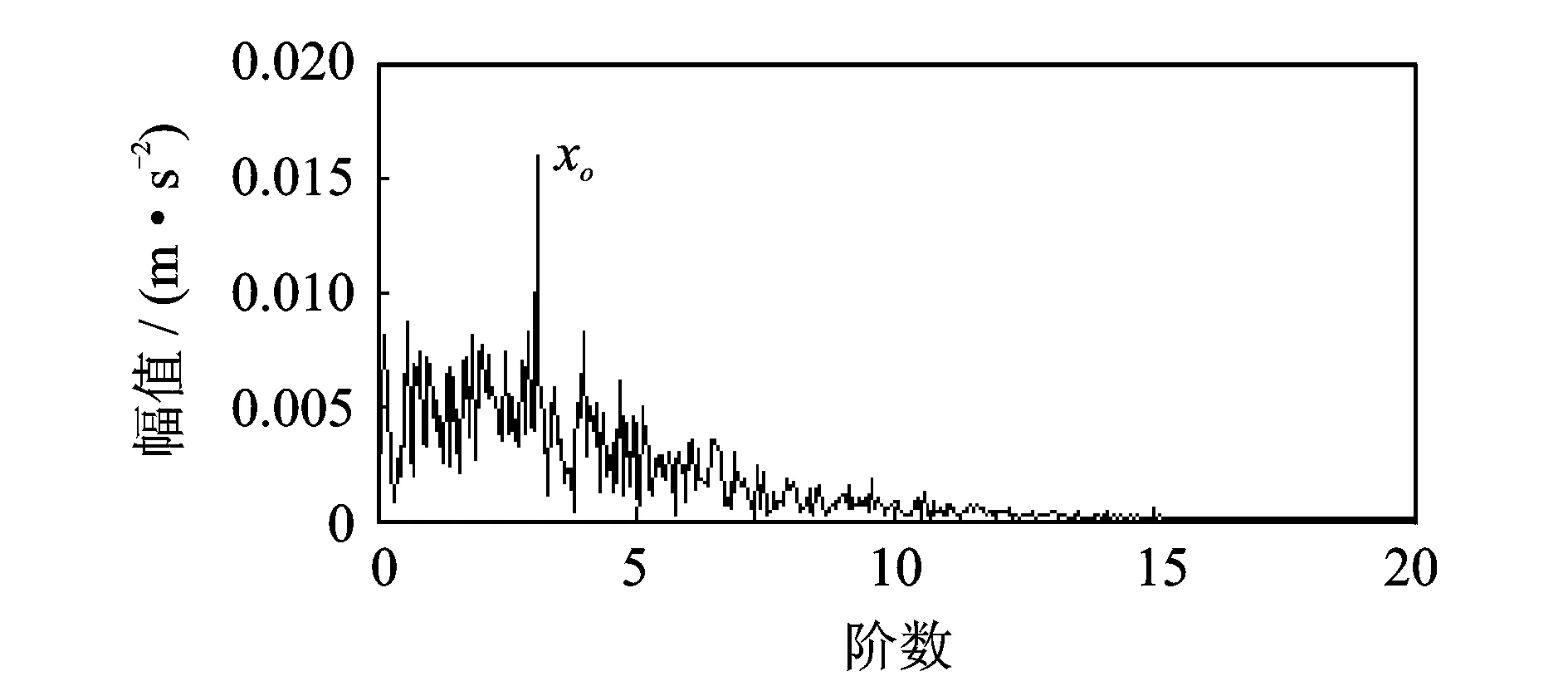
图15 图12中PF3(θ)的包络阶次谱Fig.15 The envelope order spectrum of the PF3(θ) in fig.12

图10是滚动轴承外圈局部损伤的振动加速度信号s(t)，其中采样频率为8 192 Hz，采样时间为20 s。截取5～7 s加速过程的信号s1(t)，同样采用本方法进行分析，其中，每转采样点数设为200，即最大分析阶数为100。等角度重采样后的信号s1(θ)如图11所示。进一步对s1(θ)做LMD分解，得到了7个PF分量，前3个PF分量PF1(θ)～PF3(θ)如图12所示，包含有故障特征信息。分别对其包络信号a1(θ)～a3(θ)进行频谱分析，结果分别如图13～图15所示。可以看出：图13中在外圈故障特征阶次xo=3.04的1,2,3,4倍处有明显的谱线;图14中在外圈故障特征阶次xo的1,2倍处有明显谱线;图15中在外圈故障特征阶次xo处存在明显的谱线，都说明滚动轴承外圈存在局部故障，与实际情况相符。

对于同型号正常轴承信号，采用本方法进行分析。图16是其时域波形s(t)，其中采样频率为8 192 Hz，采样时间为20 s。截取5～7 s加速过程的信号s1(t)进行分析，图17是s1(t)等角度重采样后的信号s1(θ)，其中，每转采样点数为400，即最大分析阶数为200。对s1(θ)进行LMD分解，其中PF1(θ)和PF2(θ)的包络信号a1(θ)和a2(θ)的频谱分别如图18和图19所示，从中找不到滚动轴承故障特征阶次，与实际情况相符，进一步说明了本方法的有效性。

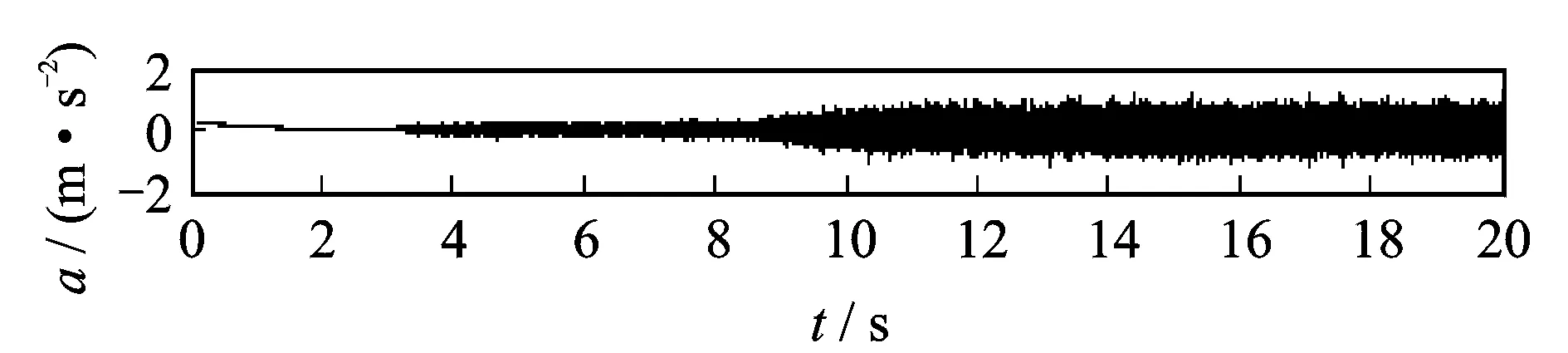
图16 正常轴承的振动信号Fig.16 The vibration signal of normal roller bearing

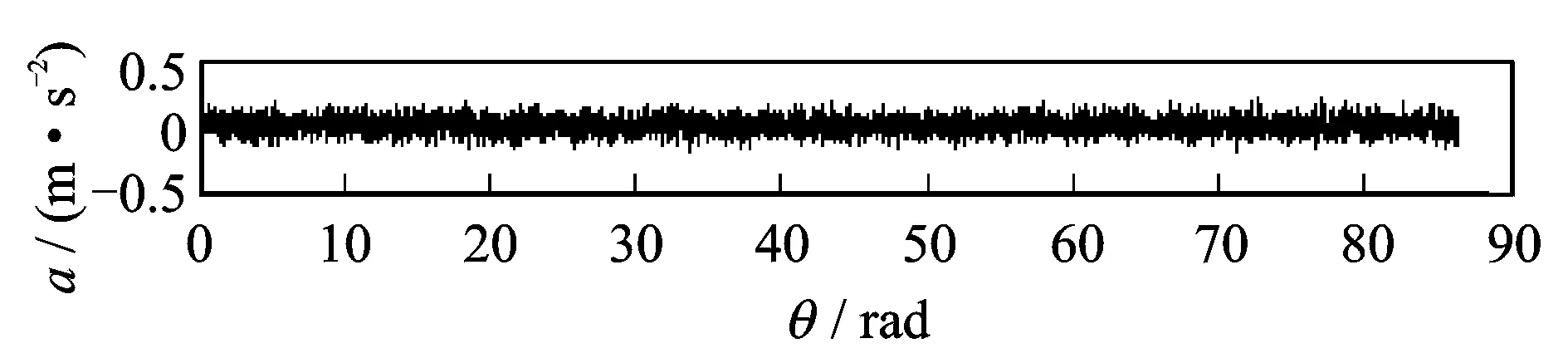
图17 阶次重采样后的正常轴承振动信号Fig.17 The vibration signal of normal roller bearing after order resampling

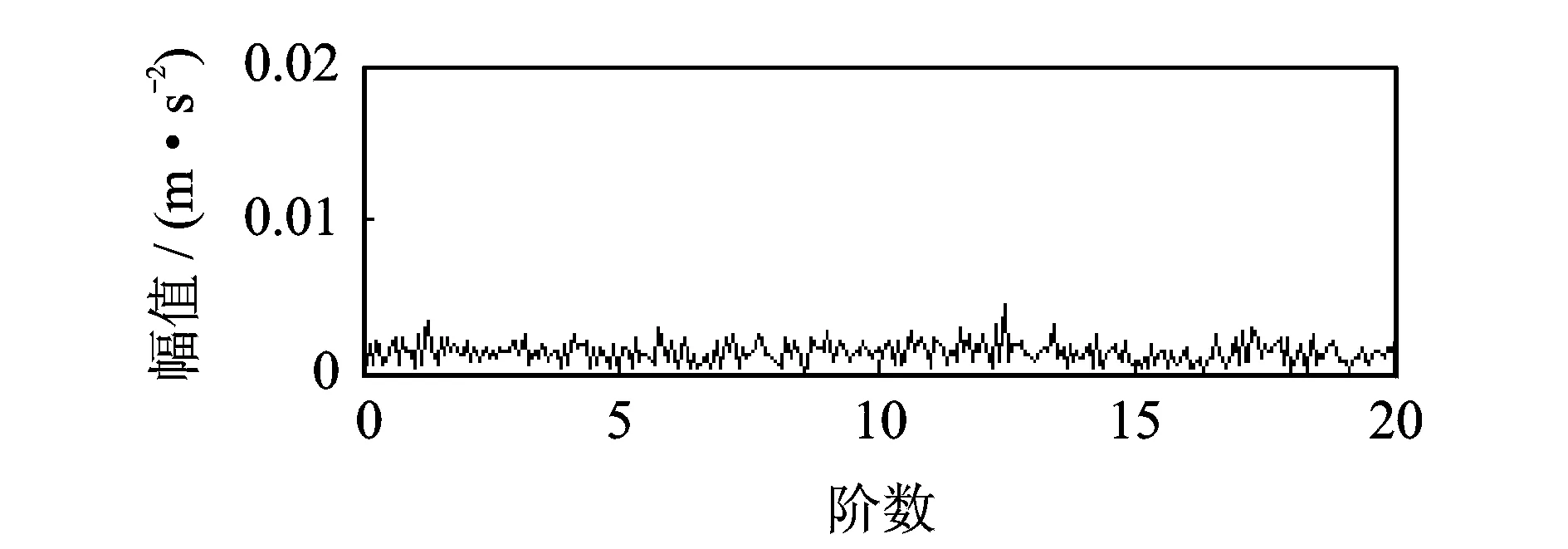
图18 第1个PF分量的包络阶次谱Fig.18 The envelope order spectrum of the first PF component

图19 第2个PF分量的包络阶次谱Fig.19 The envelope order spectrum of the second PF component

本实验中在滚动轴承上开设的是单个的轴向槽，用以验证所提方法的有效性。对于局部(即长度较短)的周向槽造成的故障特征与轴向槽相类似，因此本方法也能有效诊断。对于长度较长的周向槽，已不属于局部故障，本方法的诊断效果需要进一步研究。另外，如果内圈或外圈同时有多个槽时，滚动轴承的故障特征频率和固有频率都会发生改变，但只要通过计算或实验确定了这些频率值，使用本方法也能进行有效诊断。

3 结论

1) 在分析滚动轴承变转速状态下的振动信号时，引入阶次跟踪分析能够解决传统频谱分析方法的“频率混淆”现象，使谱图的谱线清晰可读。

2) 滚动轴承故障振动信号是一种多分量的调幅-调频信号，采用LMD方法能将其自适应地分解为若干个PF分量之和，同时得到各个PF分量的包络信号和瞬时频率，实现了原信号的完整解调。

3) 对含有滚动轴承故障特征的PF分量的包络信号进行频谱分析，能够准确地识别出故障的部位，并能有效地提取出滚动轴承故障振动信号的故障特征。

[1] 李志农, 丁启全, 吴昭同, 等. 旋转机械升降速过程的双谱-FHMM识别方法[J]. 振动工程学报, 2003, 16(2): 171-174.

Li Zhinong, Ding Qiquan, Wu Zhaotong, et al. Study on bispectrum-FHMM recognition method in speed-up and speed-down process of rotating machinery[J]. Journal of Vibration Engineering, 2003, 16(2): 171-174. (in Chinese)

[2] 康海英, 栾军英, 郑海起, 等. 基于阶次跟踪和经验模态分解的滚动轴承包络解调分析[J]. 机械工程学报, 2007, 43(8): 119-122.

Kang Haiying, Luan Junying, Zheng Haiqi, et al. Envelope demodulation analysis of bearing based on order tracking and empirical mode decomposition[J]. Chinese Journal of Mechanical Engineering, 2007, 43(8): 119-122. (in Chinese)

[3] 李辉, 郑海起, 杨绍普. 齿轮箱起动过程阶次倒双谱故障诊断方法[J]. 北京交通大学学报, 2008, 32(4): 1-5.

Li Hui, Zheng Haiqi, Yang Shaopu. Order bi-cepstrum fault diagnosis methods for gearbox during running up[J]. Journal of Beijing Jiaotong University, 2008, 32(4): 1-5. (in Chinese)

[4] 程军圣, 张亢, 杨宇. 局部均值分解方法及其在滚动轴承故障诊断中的应用[J]. 中国机械工程, 2009, 20(22): 2711-2717.

Cheng Junsheng, Zhang Kang, Yang Yu. The local mean decomposition method and its application to roller bearings fault diagnosis[J]. China Mechanical Engineering, 2009, 20(22): 2711-2717. (in Chinese)

[5] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A, 1998, 454: 903-995.

[6] Wu Z H, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society of London Series A, 2004, 460: 1597-1611.

[7] Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[8] Pegram G G S, Peel M C, McMahon T A. Empirical mode decomposition using rational splines: an application to rainfall time series[J]. Proceedings of the Royal Society of London Series A, 2008, 464: 1483-1501.

[9] He Zhi, Shen Yi, Wang Qiang. Boundary extension for Hilbert-Huang transform inspired by gray prediction model[J]. Signal Processing, 2012, 92(3): 685-697.

[10]方琨, 王渝, 马利兵, 等. 基于RO-SBM的Hilbert-Huang变换端点效应抑制方法[J]. 振动、测试与诊断, 2013, 33(2): 319-324.

Fang Kun, Wang Yu, Ma Libing, et al. Improved method for restraining end effect in Hilbert-Huang transform based on RO-SBM and its applications[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 319-324. (in Chinese)

[11]Olhede S, Walden A T. A generalized demodulation approach to time-frequency projections for multicomponent signals[J]. Proceedings of the Royal Society of London Series A, 2005, 461: 2159-2179.

[12]Jonathan S S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.

[13]郭瑜, 秦树人, 梁玉前. 时频分析阶比跟踪技术[J]. 重庆大学学报:自然科学版, 2002, 25(5): 17-21.

Guo Yu, Qin Shuren, Liang Yuqian. Order tracking method based on time-frequency analysis[J]. Journal of Chongqing University: Natural Science Edition, 2002, 25(5): 17-21. (in Chinese)

[14]Fyfe K R, Munck E D S. Analysis of computed order tracking[J]. Mechanical Systems and Signal Processing, 1997, 11(2): 187-205.

[15]郭瑜, 秦树人, 汤宝平, 等. 基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报, 2003, 39(3): 32-36.

Guo Yu, Qin Shuren, Tang Baoping, et al. Order tracking of rotating machinery based on instantaneous frequency estimation[J]. Chinese Journal of Mechanical Engineering, 2003, 39(3): 32-36. (in Chinese)

[16]Wang Yanxue, He Zhengjia, Zi Yanyang. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis[J]. Journal of Vibration and Acoustics, 2010, 132(2): 1-10.

[17]杨斌, 程军圣. 基于LMD和主分量分析的齿轮损伤识别方法[J]. 振动、测试与诊断, 2013, 33(5): 809-813.

Yang Bin, Cheng Junsheng. Fault detection method for gear condition based on LMD method and principle component[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(5): 809-813. (in Chinese)