压电谐波电机驱动系统非线性主共振分析*

李 冲， 许立忠

(燕山大学机械工程学院 秦皇岛，066004)



压电谐波电机驱动系统非线性主共振分析*

李 冲， 许立忠

(燕山大学机械工程学院 秦皇岛，066004)

为了探索压电谐波电机的机械-压电系统的非线性共振特性，设计了一种集压电驱动、谐波传动和活齿传动为一体的机电集成压电谐波电机。在非线性压电和非线性弹性效应的基础上，建立了驱动系统非线性机电耦合动力学方程。利用Linz Ted-Poincaré法推导了驱动系统非线性主共振响应方程，得出了主共振幅频响应曲线，分析了不同非线性效应对主共振响应的影响，最后通过四阶Runge-Kutta数值法验证了解析解的正确性。结果表明：在两种非线性效应中，非线性压电效应对主共振响应的影响是主要的；压电堆主共振出现在偏离固有频率较远处，且随着频率改变响应值出现跳跃现象；数值解与解析解响应曲线吻合较好。

压电电机； 谐波电机； 非线性； 主共振； Linz Ted-Poincaré法

引 言

近年来，以形状记忆合金、电致伸缩、磁致伸缩和压电主导的智能材料发展迅速，其中压电材料成为科研人员关注的热点[1]。适应于各场合的各类微型驱动装置层出不穷：Toyama[2]将安装了球形压电电机的相机用在管状探测机器上；Jeong等[3]研制了一台用在微型设备上的三足式薄状旋转压电电机；赵淳生团队研发的直径为30 mm的压电超声电机用于“嫦娥三号”光谱仪上，协助探测器在月球表面完美着陆[4]。

传统压电电机主要靠摩擦传递运动，且能输出较大转矩，但也存在接触面易于磨损、接触材料造价高等缺点[5-6]。非接触式压电电机虽避免了定转子间的摩擦，但其承载较低受到制约[7]。压电谐波电机弥补了一些不足，德国Oliver Barth设计和制造了一种利用谐波齿轮来工作的谐波型压电电机[8]，该电机能够获得0.75Nm输出转矩。辛洪兵等[9]提出了一种含有位移放大机构的压电谐波电机。Chen等[10]利用20个压电堆研制了一台类似于谐波电机的工作在径向弯曲模态的压电超声电机。李霞等[11]提出了一种新型压电谐波电机，该电机通过波发生器产生周期性运动，使柔轮产生周期性变形，从而实现电机低速转动。以上谐波电机大都采用了传统谐波齿轮传动，因而对柔轮材料的抗疲劳强度、加工等提出了较高要求。

笔者提出了一种不同类型的机电集成压电谐波电机[12]。与传统压电谐波电机相比，该电机集压电驱动、活齿传动和谐波传动于一体，通过活齿啮合取代柔轮来驱动转子，这是活齿系统在压电电机中的创新应用。驱动系统对电机的正常运转起着至关重要的作用，然而由于非线性压电效应和材料非线性弹性效应的存在，使得系统的输出也呈现非线性特性。在电机工作过程中，非线性主共振会使压电堆的输出位移和输出力发生局部变化，进而使波发生器产生的谐波不规范，使得活齿受力的规律打乱，最终影响电机的输出效率和转矩，同时会出现电机间歇性停转或者转速不稳定等问题。笔者通过Linz Ted-Poincaré解析法和四阶Runge-Kutta数值法对非线性主共振进行求解和验证。

1 机电集成压电谐波电机工作原理

机电集成压电谐波电机如图1所示，电机由驱动系统和传动系统构成。其中：驱动系统包括2个压电堆、2个弹性体和摆动体等；传动系统包括波发生器、中心轮、活齿架和30个活齿等。电机利用互为90°方位的两压电堆作驱动源。初始时刻，各零件相互接触；当给两向压电堆接入带正偏置相位差π/2的余弦信号后，压电堆开始轴向伸缩变形，弹性力带动弹性体运动，同时使摆动体朝弹簧方向移动；当压电堆零电压时，摆动体在弹簧作用下复位。同理，在摆动体两方向往复摆动下，波发生器侧面产生连续谐波，谐波力推动活齿运动进而带动活齿架转动。

图1 机电集成压电谐波电机Fig.1 An electromechanical integrated harmonic piezo-motor

2 非线性机电耦合动力学方程

考虑非线性时压电应变方程[13]为

(1)

其中：d33为压电应变常数(m/V)；lp为压电片厚度(mm)；U为驱动信号，U=Up-p[1+cos(ωt)]/2，Up-p为信号峰峰值(V)；ω为驱动频率(rad/s)；d333为非线性压电系数。

根据力和应变的关系式σp=Fp/Ap和广义胡克定律σp=c33S3，可得压电堆末端非线性输出力为

(2)

其中：c33为弹性刚度系数；Ap为压电堆横截面积。

考虑压电材料的非线性弹性效应，引入非量纲小参数ε1，则无激励时压电堆的非线性轴向应力为

(3)

其中：εy为无激励时压电堆轴向应变，且εy=∂v/∂y。

对压电堆施加激励信号时，设小参数ε2=lp/lnp，则压电堆总的内力为

(4)

其中：lnp为压电堆总长度；Fp0，Fp1，Fp2为常系数。

驱动系统动力学模型如图2所示，压电堆截面为5 mm×5 mm的矩形截面，弹性体OD梁和DB梁为6 mm×6 mm的矩形截面，而摆动体为直径为8 mm的圆截面。ε1和ε2都是小参数，令ε=ε1=ε2，对图2(a)中微元dy的受力在y向应用牛顿定律，可得压电堆轴向振动的非线性机电耦合动力学方程为

(5)

其中：ρp为压电堆密度。

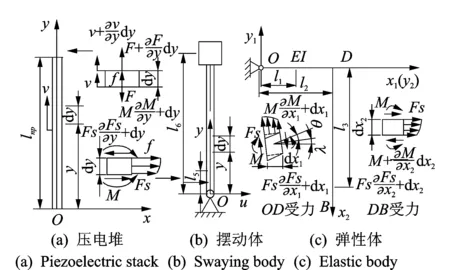
图2 驱动系统动力学模型Fig.2 Dynamics model of driving system

在图2(b,c)中，弹性体OD梁、DB梁及摆动体受到来自压电堆的非线性激振力分别为

(6)

由于OD梁和DB梁的长度与截面高度之比分别为1.83(<5)和5.83(>5)，故OD梁选用Timoshenko梁模型，而DB梁选用Euler-Bernoulli梁模型。同理，摆动体为Euler-Bernoulli梁模型。可得

(7)

其中：ρ为弹性体密度；S1为弹性体截面面积；EI，EIT为弹性体和摆动体抗弯刚度。

将各动态位移v(y,t)=φ(y)qp(t)，y1(x1,t)=φ(x1)qOD(t)，y2(x2,t)=η(x2)qDB(t)，u(y,t)=ψ(y)qs(t)代入式(5)和式(7)，并写成矩阵形式，得驱动系统非线性动力学方程为

(8)

其中：φ(y)，φ(x1)，η(x1)和ψ(y)分别为压电堆、OD梁、DB梁和摆动体的模态函数；Q为广义坐标列阵，Q=[qpqODqDBqs]T；F0，F1和F2分别为零次、一次和二次谐波激振力；B1，B2，B3为方程系数，Bi=[b1ib2ib3ib4i]。

3 非线性主共振响应

利用Linz Ted-Poincaré法对式(8)求解。Linz Ted-Poincare法是一种求解非线性方程的近似解析法，其基本思想认为非线性系统的频率并不等于派生系统的固有频率，而是关于小参数的函数，应将非线性频率写成小参数的幂级数，幂级数的系数根据周期运动规律而定。

假设系统激励频率ω接近固有频率ω0，引入频方差εσ=ω2-ω02，将原系统的解展成ε的幂级数，构成非线性系统的周期解Q(t,ε)

(9)

将频方差和式(9)代入耦合动力学方程(8)，并令ε的同次幂系数相等，导出以下近似方程组

(10)

F0+F1cosωt+F2cos2ωt

(11)

(12)

δ0为初始位移，初始速度为0，一次和二次初始位移和速度均取0。设零次近似方程式(10)的解为

(13)

由初始条件得M0=δ0，将式(13)代入式(1)得

(14)

为避免式(14)中出现久期项，必须令cosωt和sinωt的系数为0，同时代入频方差，可得

(15)

求解上式，可得N0=0，式(15)可化简为

(16)

当F1=0时，式(16)对应的曲线是主共振幅频响应的骨架线，它决定了幅频响应曲线的基本形状。

驱动部分主共振响应一次非线性近似解为

将式(13)和式(17)代入二次近似方程式(12)，令cosωt的系数为0，可得

(18)

二次近似方程解为

(19)

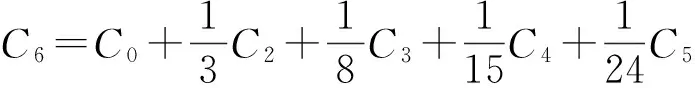
忽略二阶以上高阶项，求出驱动系统主共振非线性近似解为

(20)

因此，驱动系统各构件主共振响应位移为

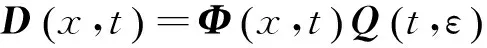
(21)

其中：D(x,t)为各构件响应位移，D(x,t)=[vy1y2u]T；Ф(x,t)为各构件模态函数，具体形式由文献[12]可得，且Ф(x,t)=[φ(y)φ(x1)η(x2)ψ(y)]T。

4 算例求解与分析

4.1 幅频特性分析

当激励信号峰峰值Up-p>0且激励频率ω接近固有频率ω0时，系统在压电激振力下产生共振。驱动系统的线性固有频率在文献[12]中进行了求解，一阶线性主共振频率为213 785 rad/s。取小参数ε=0.2，初始位移激励δ0=6×10-4m，将表1参数代入式(16)，分别选择Up-p=0和Up-p=150 V时的F1值作驱动系统主共振幅频特性曲线，分别用虚线和实线表示，见图3。图中F1=0时的曲线为频响曲线的骨架线，骨架线左侧相当于与外激励同相，右侧相当于与外激励反相。分析图3得出以下结论。

图3 驱动系统幅频响应Fig.3 Amplitude-frequency responses of the driving system

1) 在压电堆幅频响应中，非线性共振不出现在ω=ω0及其附近，而是出现在偏离ω0较远处。当ω恒定时，对应的振幅可以取到3个值，这即是非线性系统中的跳跃现象。幅频响应中的骨架线主导了频响曲线的形状，反映了不同激励下振幅与激励频率的关系，且F1越大时频响曲线偏离骨架线越远。

2) 在OD梁、DB梁和摆动体幅频响应中，骨架线变成了稳定在ω0处的一条直线，骨架线两侧的共振曲线对称分布，这是因为在耦合动力学方程中影响骨架线走势的b23，b33和b43均为0，OD梁、DB梁和摆动体的非线性来自通入激励时产生的非线性压电效应，不受材料非线性弹性效应的影响。由图3可看出，OD梁、DB梁和摆动体激励力依次减弱。

4.2 主共振响应分析

将表1所示的驱动系统参数代入式(21)，求得主共振非线性与线性动态响应如图4所示。其中压电堆存在非线性弹性和非线性压电效应，故按照同时存在两种非线性效应、只存在非线性弹性效应或非线性压电效应、线性4种情况进行对比分析；OD梁、DB梁和摆动体只存在压电非线性效应，故只对存在非线性压电效应和线性时进行对比。由图可知以下几点。

表1 驱动系统参数

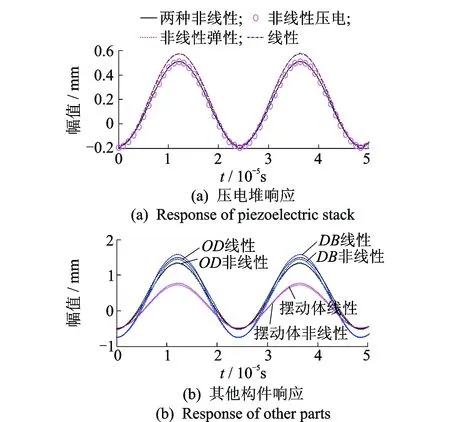
图4 驱动系统主共振位移响应Fig.4 Amplitude-frequency responses of driving system

1) 由于激励信号是带有偏置的余弦信号，故各构件位移响应中曲线的平衡位置偏离零点，在各构件中DB梁的平均振幅最大。

2) 各构件非线性与线性响应曲线基本吻合，振幅存在差异，且都是线性振幅大于非线性振幅，这是因为非线性效应的存在使得激励力效果减弱，类似于软弹簧系统。

3) 在压电堆4种情况比较中，同时存在两种非线性时，与线性振幅差值最大为10.4%；只存在非线性弹性或者非线性压电时，与线性振幅差值分别为2.6%和9.1%。可见非线性压电效应是非线性弹性效应影响力的3.5倍，非线性压电效应对压电堆主共振起主导作用，故在对驱动系统其他构件分析时只考虑压电非线性是合理的。

4)OD梁、DB梁和摆动体的非线性振幅与线性振幅之差分别为9.9%，8.5%和3.2%。在驱动部分各构件中，按照压电堆、OD梁、DB梁及摆动体的顺序，非线性对振幅的影响依次减弱。

5 数值验证

利用Matlab的四阶Runge-Kutta指令对驱动系统动力学方程(8)进行数值求解，图5为通过数值法得到的压电堆主共振跳跃现象，图6为驱动系统各构件对应的相图，图7为驱动系统主共振时域响应数值解与解析解的对比。由图5～图7得出以下规律。

1) 随着激励频率ω的增大，压电堆主共振响应先增大；当ω增大到213 768rad/s时，响应值突然向上跳跃；ω继续增大，响应逐渐减小。数值模拟验证了非线性中的跳跃现象。

2) 驱动系统主共振相图曲线是由一系列椭圆曲线叠加而成，曲线呈闭合状，是外加激励频率与固有频率共同作用形成的周期运动。各构件响应的相图收敛于闭合曲线，可见驱动系统的动力学方程的解是收敛的，振幅是稳定的。

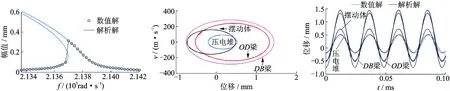
图5 压电堆主共振跳跃现象

Fig.5 The jumping phenomenon of the primary resonance for piezoelectric stack

图6 驱动系统主共振相图

Fig.6 The phase diagram of the primary resonance for driving system

图7 解析解与数值解对比

Fig.7 Comparison of analytical solution and numerical solution

3) 在解析解与数值解对比图中，压电堆数值解比解析解的振幅大3.3%。随着时间的增加，数值解与解析解之间的相位差变大，在0.1ms时相位差达到0.17π。OD梁、DB梁及摆动体数值解与解析解响应曲线吻合较好，误差可忽略。

6 结 论

1) 压电堆非线性共振出现在偏离ω0较远处，而弹性体和摆动体共振仍出现在ω0处。

2) 在两种非线性效应中，非线性压电效应对主共振响应的影响是主要的，在对驱动系统各构件主共振分析时只考虑压电非线性是合理的。

3) 数值模拟验证了非线性跳跃现象的存在，主共振响应解析解与数值解吻合较好，验证了本研究理论推导的正确性。

[1] Liu Xiujuan, Zhou Kechao, Zhang Xiaoyong, et al. Development, modeling and application of piezoelectric fiber composites[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(1): 98-107.

[2] Toyama S. Spherical ultrasonic motor for pipe inspection robot[J]. Applied Mechanics and Materials, 2012, 186: 3-11.

[3] Jeong S, Cheon S, Park J, et al. Design and fabrication of three touch point thin ultrasonic rotary motor[J]. Ferroelectrics, 2014, 459(1): 143-152.

[4] 沈大雷. 南航助“嫦娥”完美登月[N]. 中国教育报, 2013-12-18(8).

[5] 赵淳生. 21世纪超声电机技术展望[J]. 振动、测试与诊断，2000, 20(1): 7-12.

Zhao Chunsheng. Ultrasonic motor techniques in the 21st century[J]. Journal of Vibration, Measurtment & Diagnosis, 2000, 20(1): 7-12. (in Chinese)

[6] 刘传会, 丁庆军, 胡家玲, 等. 聚苯酯改性聚偏氟乙烯基超声电机摩擦材料[J]. 振动、测试与诊断，2013, 33(S2): 49-51.

Liu Chuanhui, Ding Qingjun, Hu Jialing, et al. Research on properties of POB filled PVDF-based friction materials of ultrasonic motor[J]. Journal of Vibration, Measurtment & Diagnosis, 2013, 33(S2): 49-51. (in Chinese)

[7] 季叶, 赵淳生. 一种具有高转速的新型非接触式超声电机[J]. 压电与声光, 2006, 28(5): 527-529.

Ji Ye, Zhao Chunsheng. A new type non-contact ultrasonic motor with higher revolution speed[J]. Piezoelectrics & Acoustooptics, 2006, 28(5): 527-529. (in Chinese)

[8] Barth O. Harmonic piezodrive-miniaturized servo motor[J]. Mechatronics, 2000, 10(4): 545-554.

[9] 辛洪兵, 郑伟智. 压电谐波电机的研究[J]. 压电与声光, 2004, 26(2): 122-125.

Xin Hongbing, Zhang Weizhi. Study on harmonic piezomotor[J]. Piezoelectrics & Acoustooptics, 2004, 26(2): 122-125. (in Chinese)

[10]Chen Weishan, Liu Yingxiang, Yang Xiaohui, et al. Ring-type traveling wave ultrasonic motor using a radial bending mode[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2014, 61(1): 197-202.

[11]李霞, 郭正阳, 张三川, 等. 一种新型压电谐波电动机的研究[J]. 微特电机, 2014, 42(6): 4-7.

Li Xia, Guo Zhengyang, Zhang Sanchuan, et al. Research on a novel piezoelectric harmonic motor[J]. Small & Special Electrical Machines, 2014, 42(6): 4-7. (in Chinese)

[12]Li Chong, Xing Jichun, Xu Lizhong. Coupled vibration of driving sections for an electromechanical integrated harmonic piezodrive system[J]. AIP Advances, 2014, 4(3): 031320.

[13]Tan Ping, Tong Liyong. A one-dimensional model for non-linear behaviour of piezoelectric composite materials[J]. Composite Structures, 2002, 58(4): 551-561.

10.16450/j.cnki.issn.1004-6801.2016.03.027

*国家自然科学基金资助项目(51275441)；河北省研究生创新资助项目(00302-6370001)

2015-05-13；

2015-09-08

TH113.1

李冲，男，1988年6月生，博士生。主要研究方向为新型压电驱动及动力学分析。曾发表《Coupled vibration of driving sections for an electromechanical integrated harmonic piezodrive system》(《AIP Advances》2014，Vol.4，No.3)等论文。

E-mail: lichong1237@126.com