SFD作用下故障转子系统动力学特性及混沌控制*

2016-11-23张俊红

振动、测试与诊断 2016年3期

关键词：油膜阻尼器频谱

王俊，马梁，，张俊红，，鲁鑫

(1.天津大学仁爱学院天津,301636) (2.天津大学内燃机燃烧学国家重点实验室天津，300072)

SFD作用下故障转子系统动力学特性及混沌控制*

王俊1，马梁1，2，张俊红1，2，鲁鑫2

(1.天津大学仁爱学院天津,301636) (2.天津大学内燃机燃烧学国家重点实验室天津，300072)

考虑挤压油膜阻尼器(squeeze film damper，简称SFD)作用，研究碰摩故障及不对中-碰摩耦合故障下系统动力学特性及SFD对系统混沌运动控制。基于Lagrange方程，建立不对中-碰摩耦合故障下SFD-转子-滚动轴承系统动力学模型，采用龙格库塔法对模型求解，并利用分岔图、Poincaré图、频谱图等进行对比分析。研究结果表明：合理油膜间隙下的SFD能有效抑制系统非协调响应以及振动幅值，使故障转子系统的混沌运动控制在稳定周期轨道上;过小的油膜间隙会形成很强的非线性油膜支反力，产生非协调频率成分，使稳定周期系统重返混沌状态；随着油膜间隙减小，SFD对不对中故障产生的典型2X，3X，4X和5X频幅值具有不同影响，其中2X频幅值变化明显，3X和4X频幅值变化微弱，5X频幅值基本不变。

挤压油膜阻尼器；耦合故障；转子-滚动轴承系统；混沌控制

引言

近年来，随着SFD在转子系统中的广泛应用，研究SFD对转子系统动力学特性的影响逐渐成为一个热点问题[1-2]。当转子系统出现故障(如不对中、碰摩等)时，会产生次谐波、高次谐波等非协调分量，形成混沌运动。因此，研究SFD对故障产生混沌运动的控制有着重要的理论和应用价值。

Humes[3]基于Reynolds方程的端轴承假设研究了带有SFD的刚性转子系统的运动规律，提出了流体油膜力的理论模型，并将其应用到转子系统模型中，所得结果与实验结果较为吻合。周海仑等[4]建立了SFD-滚动轴承-转子耦合系统动力学模型，采用数值积分法得到系统的非线性动力学响应，发现在转子系统较大的油膜间隙、较高的转速以及较大的支承刚度下容易进入概周期运动。张家忠等[5-6]考虑挤SFD的作用，建立了滑动轴承支承下的单盘Jeffcott转子系统动力学模型，采用数值积分法研究了SFD对系统减振特性的影响，发现挤压油膜阻尼器能有效改变转子系统的分岔行为，提高转子系统发生失稳时的转速。张韬等[7]研究了有SFD、转静子碰摩和转轴横向裂纹多种非线性因素作用下的转子系统故障的非线性特性。林富生等[8]研究了SFD支承的单盘转子系统碰摩特性。以上关于SFD对故障的研究或是基于SFD-转子-轴承系统模型，或主要集中在混沌道路现象的分析以及SFD的减振特性，并未研究SFD对混沌的控制作用以及SFD对不对中故障特性的影响。

笔者采用数值方法研究了SFD对碰摩单一故障及不对中-碰摩耦合故障转子系统混沌运动的控制作用，并通过频谱图分析了SFD对不对中故障特征频率的影响。

1 系统模型与基本理论

1.1 转子动力学微分方程

图1所示为考虑不对中-碰摩耦合故障的SFD-转子-滚动轴承-花键联轴器耦合系统动力学模型，转子采用深沟球轴承支承。其中：Ms1，Md1，Ms2，Ms3，Ms4，Ms5，Md2和Ms6分别为转子等效集中质量；Mo1和Mo2为滚动轴承外圈处的集中质量；K为弹性轴刚度；Ka为鼠笼弹性支撑刚度；Cz和Cp为转子在轴承、圆盘处阻尼系数；δ为转子与静子的间隙；e1和e2为圆盘偏心距；α1和α2为圆盘偏心角；ks为碰摩刚度[9]。

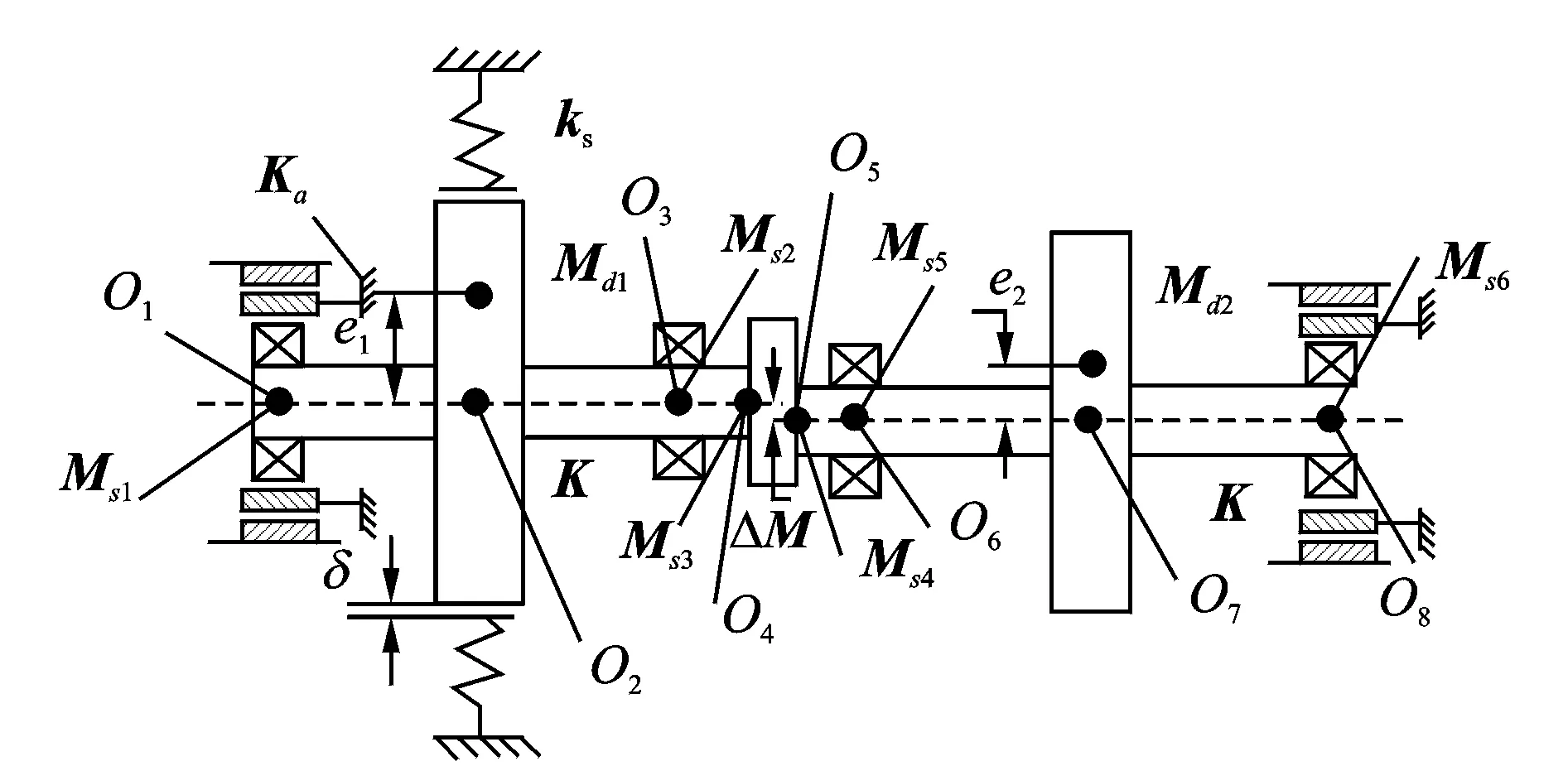
图1 SFD-转子-轴承系统简化模型Fig.1 The simplified model of rotor bearing system

根据Lagrange方程可得系统运动微分方程

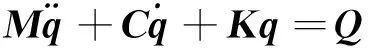
(1)

其中：q=[Xs1Ys1Xd1Yd1Xs2Ys2Xs3Ys3Xs4Ys4Xs5Ys5Xd2Yd2Xs6Ys6Xo1Yo1Xo2Yo2]T；Q=[Fbx1Fby1Px1+FpxPy1+FpyFbx2Fby2FLXFLY-FLX-FLYFbx3Fby3Px2Py2Fbx4Fby4Fsx1-Fbx1Fsy1-Fby1Fsx2-Fbx4Fsy2-Fby4]T；Fbx1，Fby1，Fbx2，Fby2，Fbx3，Fby3，Fbx4和Fby4为轴承支反力；Px1，Py1，Px2和Py2为圆盘偏心力；Fpx，Fpy为碰摩力；FLX，FLY为花键联轴器不对中力；Fsx1，Fsy1，Fsx2和Fsy2为挤压油膜阻尼器的支反力;M，C和K为系统的质量矩阵、阻尼矩阵和刚度矩阵。

引入无量纲变换[9]

其中：ω为转子转动角速度；μ为滚动轴承游动间隙。

式(1)经无量纲变换为

(2)

1.2 碰摩力模型

假定转子已处于碰摩状态，转子与定子的摩擦符合库仑定律[9-12]。

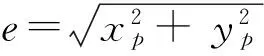
(3)

其中：ks为碰摩刚度；f为摩擦因数。

将碰摩力在x-y坐标系中分解

(4)

1.3 花键联轴器不对中啮合力模型

图2所示为花键联轴器模型，由参考文献[13]可得每个键扭转产生的啮合力为

(5)

(6)

其中：φ为各键变形产生的扭转角位移；T为扭矩；z为花键联轴器键的个数；Li，KLi分别为各键等效啮合距离和刚度；R为键根圆半径[9]。

动态位移产生的啮合力为

(7)

(8)

(9)

其中：φi为各键与X轴正向夹角；e′为联轴器动态径向位移。

综合以上分析，得联轴器不对中产生的啮合力

(10)

联轴器不对中产生的x，y向合力为

(11)

(12)

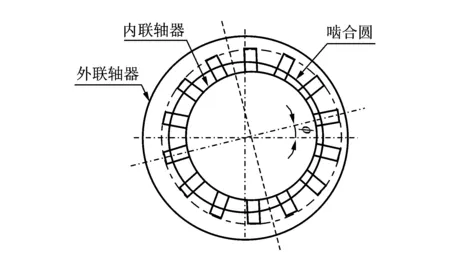
图2 花键联轴器模型Fig.2 Spline coupling model

1.4 SFD油膜力模型

SFD油膜力计算可以根据流体动压润滑理论求得，依据雷诺方程可以导出SFD的油膜压力的分布，SFD的瞬态雷诺方程[14]可以由式(13)求得

(13)

其中：p为为油膜压力分布；Rs为阻尼器半径；μs为滑油黏度；h为油膜厚度；z为轴颈的轴向位移；Ω为轴颈的进动角速度。

采用短轴承理论,并通过Sommerfeld变换可得油膜支承力

(14)

其中：

1.5 滚动轴承力模型

设轴承滚珠在内外滚道间等距排列，滚珠与滚道之间为纯滚动。由于不平衡激励的作用，滚动轴承做强迫振动，振动频率等于转子旋转频率。同时在旋转过程中，滚动轴承刚度会发生周期性变化，产生VC振动[15]，该振动为参数激振。

基于Hertz弹性接触理论，参考文献[16-17]可得滚动轴承作用力为

(15)

1.6 模型计算参数

根据以上模型，建立不对中碰摩耦合故障下SFD-转子-滚动轴承系统动力学方程，设置系统参数初始值，运用龙格库塔法进行求解。系统各部分参数如表1～表5[9]所示。

表1 转子参数

表2 碰摩参数

表3 花键联轴器参数

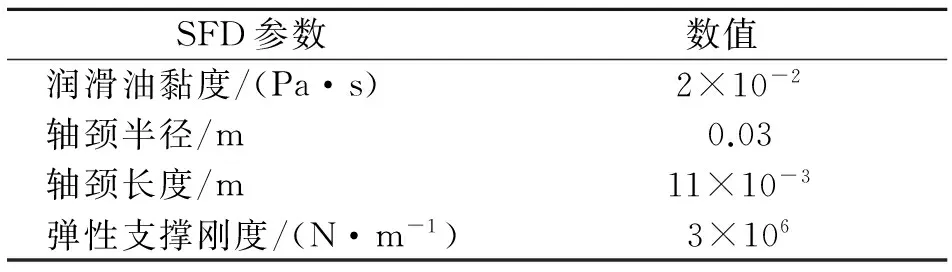
表4 SFD参数

表5 滚动轴承参数

2 结果分析

2.1 SFD-转子-滚动轴承系统的动力学特性分析

采用数值积分法求解SFD作用下系统的动力学响应，其中弹性支承的刚度Ka=3×106N/m，其余参数见表1～表5。分析图3和表6可知，SFD能有效减小转子系统共振时的幅值。当挤压油膜阻尼器的间隙大于等于5×10-5m时，随着油膜间隙的逐渐减小，系统共振幅值逐渐减小；当间隙等于5×10-5m时，共振幅值减小了约55.64%；当油膜间隙等于4×10-5m时，其共振幅值突然变大，减振效果呈现相反趋势。

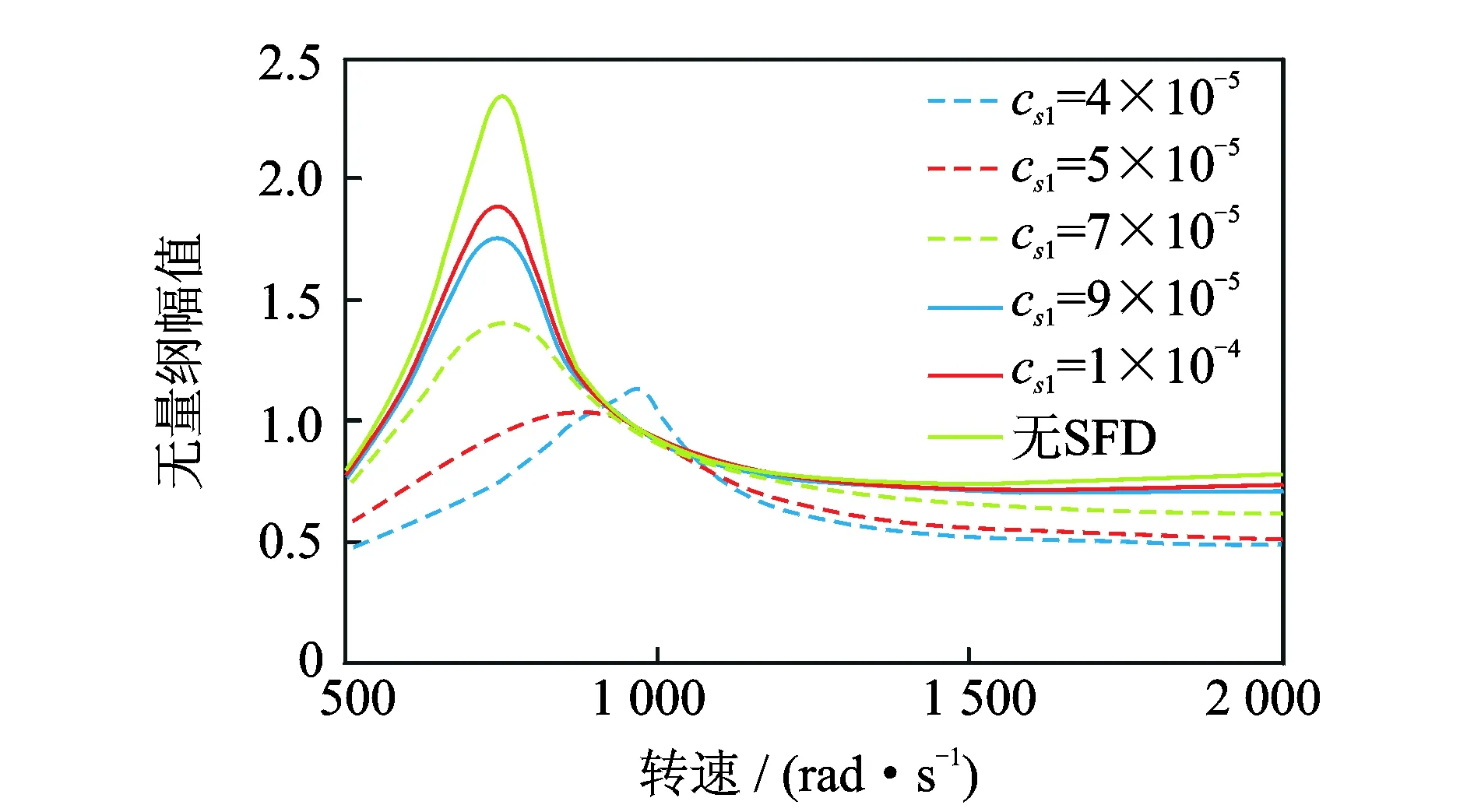
图3 不同油膜间隙下系统响应幅频特性Fig.3 Amplitude frequency characteristic of system response under different oil film gap

Tab.6 Amplitude frequency characteristic of system response under different oil film gap

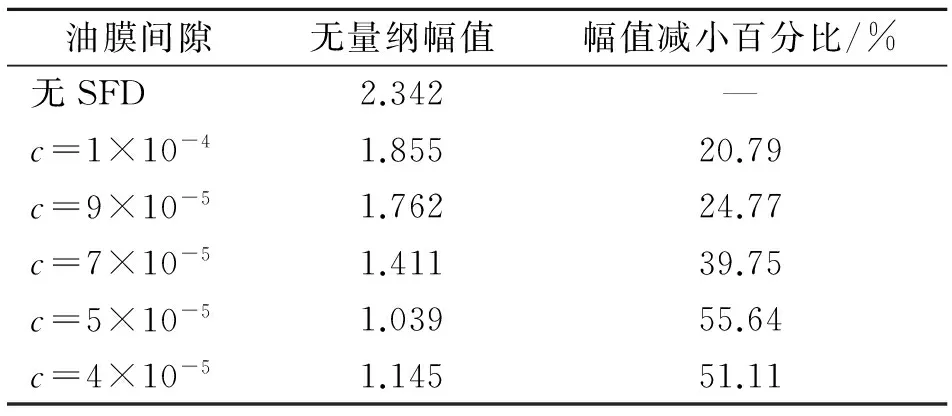
油膜间隙无量纲幅值幅值减小百分比/%无SFD2.342—c=1×10-41.85520.79c=9×10-51.76224.77c=7×10-51.41139.75c=5×10-51.03955.64c=4×10-51.14551.11

图4所示共振转速为970 rad/s时，不考虑挤压油膜阻尼器的影响和考虑挤压油膜阻尼器不同油膜间隙下系统响应频谱图。由图可知，无SFD时，频谱图中存在单一的一倍频成分，考虑SFD的影响时，频谱图中出现了很多非协调频率成分，且一倍频的幅值大于不考虑SFD时系统响应的一倍频幅值。

由以上分析可知，当SFD油膜间隙在一定范围内时，其具有明显的减振效果，且随着间隙的减小，其减振效果也越好。但过小的油膜间隙会使SFD产生很强的非线性油膜支反力，形成很多非协调频率成分，使系统振动幅值增大，容易引发系统发生故障。所以在设计挤压油膜阻尼器时，合适的油膜间隙至关重要。

2.2 碰摩故障下SFD-转子-滚动轴承系统的动力学特性分析

图5(a)所示为不考虑SFD时，碰摩故障转子-

滚动轴承系统响应随转速变化的分岔图。其中油膜间隙c=1×10-4m，其余参数见表1～表5。由图可知，在转速小于等于2 690 rad/s时，系统表现为单周期运动，并在转速为1 810 rad/s附近出现跳跃；在转速ω∈(2 690, 3 000) rad/s时，系统响应出现单周期与混沌交替的现象，即表现为阵发性混沌。图5(b)所示为考虑SFD时，碰摩故障转子-滚动轴承系统响应随转速变化的分岔图。对比图5(a)可知， SFD能有效抑制碰摩故障产生的非协调响应频率成分，使原系统混沌运动变为周期和拟周期运动。

基于以上碰摩故障下转子随转速变化分岔图的对比分析，取转速ω=2 850 rad/s，进一步研究碰摩故障下SFD对系统混沌的控制作用。图6所示为碰摩故障下转子随油膜间隙变化分岔图。由图可知，系统在油膜间隙等于9.6×10-5m时发生分岔。当c≤9.6×10-5m时，系统表现为单周期运动；当c>9.6×10-5m时，系统表现为三倍周期运动。图7所示为不考虑SFD和考虑SFD时不同油膜间隙下系统响应的Poincaré图和频谱图。由图7(a)可知，不考虑SFD时系统响应的Poincaré表现为成片无规则的散状点，频谱图表现为不规则的、波动的、连续的谱线，系统处于混沌运动状态。考虑SFD，取油膜间隙c=1×10-4m，由图7(b)可知，系统响应的Poincaré表现为孤立的三点，频谱图出现1/3倍频，系统处于三倍周期运动状态。在混沌吸引子内，有无数的不稳定周期轨与混沌运动同时存在，有序运动和无序运动相互结合，相互转换。由于挤压油膜阻尼器的作用，有效地抑制了碰摩故障引起的系统非协调响应，改变了转子系统动力学方程解的拓扑结构，使其向周期解发展，将由碰摩故障引起的混沌系统稳定在3倍周期轨道上。减小油膜间隙，取c=3×10-5m，由图7(c)可知，系统响应Poincaré表现为孤立一点，频谱图表现为单一基频成分，系统做单周期运动。由于SFD的减振作用，使系统振动幅值减小，避免了系统碰摩故障发生，从而使系统运动稳定在周期1轨道上。

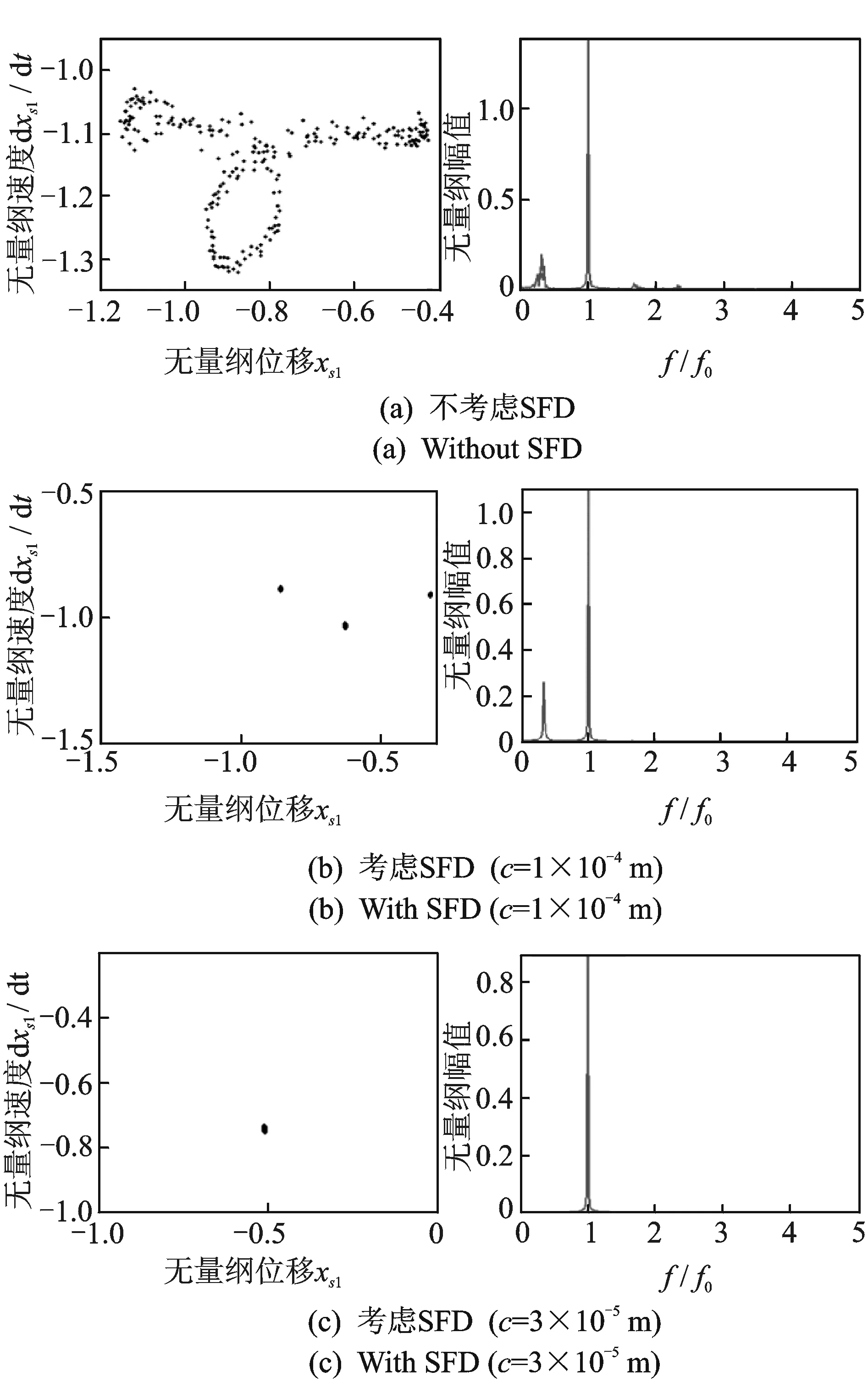
图7 碰摩故障下系统响应Poincaré图和频谱图Fig.7 Poincaré diagram and spectrum diagram of system response under the rub impact fault

2.3 不对中碰摩耦合故障SFD-转子-滚动轴承系统动力学特性分析

图8(a)所示为不考虑SFD时，不对中-碰摩耦合故障转子-滚动轴承系统响应随转速变化分岔图。其中油膜间隙c=1×10-4m，其余参数见表1～表5。由图可知，在转速小于等于1 820 rad/s时，系统表现为单周期运动；随着转速的继续升高，当ω∈(1 820,2 370) rad/s时，系统由单周期变为混沌运动，同时系统响应的最大幅值在分岔点处出现瞬时较强的跳跃；当转速大于2 370 rad/s时，系统倒分岔为两倍周期运动。图8(b)所示为考虑SFD时，不对中-碰摩耦合故障转子-滚动轴承系统响应随转速变化的分岔图。对比图8(a)可知，由于SFD的作用，使原系统发生跳跃时转速向后推移致1 900 rad/s，系统更加稳定。同时SFD有效抑制耦合故障产生的非协调响应，使原系统混沌运动变为倍周期运动，减小了系统混沌运动区间。

图8 不对中-碰摩耦合故障下转子随转速变化分岔图Fig.8 Bifurcation diagram of rotor with rotating speed under misalignment-rubbing impact coupling faults

基于以上不对中-碰摩耦合故障下转子随转速变化分岔图对比分析，取转速ω=2 200 rad/s，进一步研究不对中-碰摩耦合故障下SFD对系统混沌的控制作用。图9所示为不对中-碰摩耦合故障下转子随油膜间隙变化分岔图。由图可知，当油膜间隙c≤4.6×10-5m时，系统表现为混沌运动；当c∈(4.6×10-5, 8.1×10-5] m时，系统表现为三倍周期运动；当c>8.1×10-5m时，系统再次进入混沌运动。图10所示为不考虑SFD和考虑SFD时不同油膜间隙下系统响应的Poincaré图和频谱图。由图10(a)可知，不考虑SFD时系统响应的Poincaré表现为两片无规则的密集点，频谱图表现为不规则的、波动的、连续的谱线，系统处于混沌运动状态。考虑SFD，油膜间隙为8×10-5m，由图10(b)可知，系统响应Poincaré表现为孤立三点，频谱图出现1/3，2/3倍频，系统处于三倍周期运动。在混沌吸引子内，有无数的不稳定周期轨与混沌运动同时存在，通过挤压油膜阻尼器的作用，有效地抑制了不对中-碰摩耦合故障引起的系统非协调响应，改变了转子系统动力学方程解的拓扑结构，使其向周期解发展，将由不对中-碰摩耦合故障引起的混沌运动稳定在3倍周期轨道上。减小油膜间隙，取c=3×10-5m，由图10(c)可知，系统响应Poincaré表现为一片无规则的散状点，频谱图表现为不规则的、波动的、连续的谱线，系统处于混沌运动状态。由于在过小的油膜间隙下系统产生了很强的非线性，改变了转子系统动力学方程解的拓扑结构，使其向不稳定状态发展，重返混沌状态。

图9 不对中-碰摩故障下转子随油膜间隙变化分岔图Fig.9 Bifurcation diagram of rotor with oil film gap under misalignment-rubbing impact coupling faults

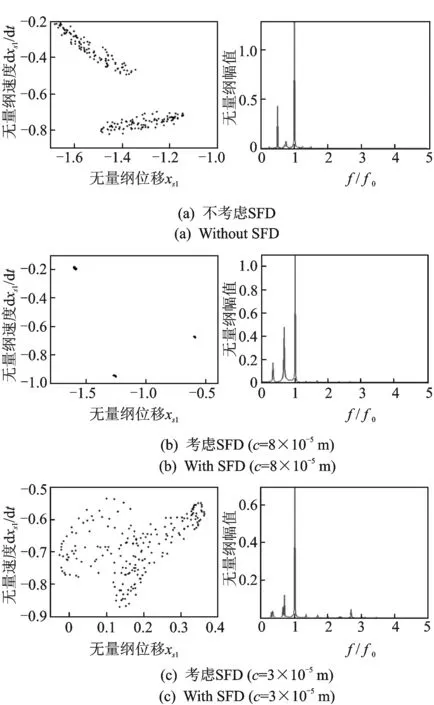
图10 不对中-碰摩耦合故障下系统响应的Poincaré图和频谱图Fig.10 Poincaré diagram and spectrum diagram of system response under misalignment-rubbing impact coupling faults

图11所示为在转速ω=1 000 rad/s时，不对中-碰摩耦合故障下，SFD对其中不对中故障引起的特征频率变化图。由图可知，在油膜间隙c≥6×10-5m时，不对中主要表现为2X频成分。3X，4X，5X频成分依次减弱。随着油膜间隙逐渐减小，2X频幅值不断减小，且变化明显，在油膜间隙小于4×10-5m时，其幅值小于4X频幅值。此外3X频幅值随着油膜间隙的逐渐减小其幅值呈现微弱的增加；4X频幅值先增大后减小，且变化不明显；而5X频幅值基本保持不变。桑潇潇等[18]利用试验研究了SFD对不对中故障的影响，所得试验结果与本研究仿真结果相吻合。

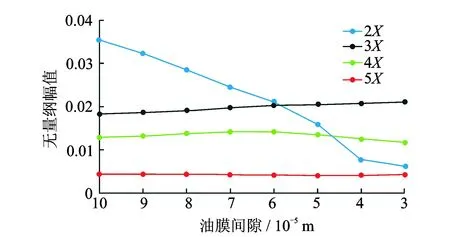
图11 油膜间隙变化对不对中特征频率的影响Fig.11 Effect of oil film gap on characteristic frequency of misalignment

3 结论

1) 对于碰摩故障转子系统，SFD能有效抑制碰摩故障产生的非协调频率，改变转子系统动力学方程解的拓扑结构，使其向周期解发展，将由碰摩故障引起的混沌系统稳定在3倍周期轨道上。减小油膜间隙，由于SFD的减振作用，使系统振动幅值减小，避免了系统碰摩故障的发生，从而使系统的运动稳定在周期1轨道上。

2) 对于不对中碰摩耦合故障转子系统，SFD有效抑制了不对中碰摩耦合故障引起的非协调响应，改变了转子系统动力学方程解的拓扑结构，使其向周期解发展，将由不对中碰摩耦合故障引起的混沌系统稳定在3倍周期轨道上。减小油膜间隙，则SFD在过小的油膜间隙下产生很强的非线性，改变了转子系统动力学方程解的拓扑结构，使其向不稳定状态发展，重返混沌状态。

3) 对于不对中-碰摩耦合故障转子系统中典型不对中特征频率，随着油膜间隙的减小，SFD对不对中故障产生的2X，3X，4X和5X频幅值具有不同的影响。其中：2X频幅值不断减小，且变化明显；3X频幅值表现出微弱的增加；4X频幅值先增大后减小，变化不明显；5X频基本保持不变。所得结果与文献[18]试验结果保持一致。

[1] 黄文虎，夏松波，刘瑞岩，等.设备故障诊断原理、技术及应用[M].北京:科学出版社, 1997：77-104.

[2] Olove B. Non-linear behavior of a flexible shaft partly supported by SFD[J]. Wear, 1997,206:255-260.

[3] Humes B. The non-linear performance of squeeze film bearings[D]. Brighton of United Kingdom: University of Sussex, 1997.

[4] 周海仑,罗贵火,陈果，等.挤压油膜阻尼器-滚动轴承-转子耦合系统的非线性响应分析[J]. 机械科学与技术, 2013, 32(4): 499-505.

Zhou Hailun, Luo Guihuo, Chen Guo, et al. Nonlinear dynamic analysis of a rotor supported on the ball bearings with squeeze film dampers[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(4): 499-505. (in Chinese)

[5] 张家忠,郑铁生,许庆余.在滑动轴承转子系统中挤压油膜阻尼器的减振特性分析[J].西安交通大学学报,1997,31(4):12-17.

Zhang Jiazhong, Zheng Tiesheng, Xu Qingyu. Theoretical study on dynamical characteristics of the rotor-fluid bearing system with squeeze film damper[J]. Journal of Xi′an Jiaotong University, 1997,31(4):12-17. (in Chinese)

[6] 张家忠,许庆余,郑铁生.阻尼器-滑动轴承-转子系统的非谐调运动及突跳特性分析[J].航空动力学报,1998,13(2):165-169.

Zhang Jiazhong, Xu Qingyu, Zheng Tiesheng. Nonsynchronous motion and jump phenomenon of rotor-fluid film bearing system with squeeze film damper[J]. Journal of Aerospace Power, 1998,13(2):165-169. (in Chinese)

[7] 张韬,孟光.有挤压油膜阻尼器支承的多故障转子系统的非线性响应特性研究[J].机械科学与技术,2004,23(1):11-14.

Zhang Tao, Meng Guang. Nonlinear characteristics of the responses of an SFD supported rotor with many malfunctions[J]. Mechanical Science and Technology, 2004,23(1):11-14. (in Chinese)

[8] 林富生,张韬,孟光.挤压油膜阻尼器-碰摩转子系统的非线性特性研究[J].振动与冲击,2004,23(1):12-17.

Lin Fusheng, Zhang Tao, Meng Guang. Nonlinear characteristics of the rub-impact response of a rotor system supported on squeeze film dampers[J]. Journal of Vibration and Shock, 2004,23(1):12-17. (in Chinese)

[9] 曹树谦，王俊，韩研研，等.耦合故障转子系统的降维及动力学特性[J].天津大学学报，2015,48(4):318-327.

Cao Shuqian, Wang Jun, Han Yanyan, et al. Dimension reductions and dynamic characteristics of rotor system with coupling faults[J]. Journal of Tianjin University,2015,48(4):318-327. (in Chinese)

[10]李朝峰,李小彭,马辉,等.非线性连续转子轴承系统碰摩故障动力学行为研究[J].振动工程学报,2009,22(4):395-399.

Li Chaofeng, Li Xiaopeng, Ma Hui, et al. The nonlinear dynamic behavior of a rotor-bearing system with rub-impact by a continuous model[J]. Journal of Vibration Engineering, 2009,22(4):395-399. (in Chinese)

[11]袁惠群,王正浩,闻邦椿.弹性机匣双盘碰摩转子系统的稳定性[J].振动与冲击,2010,29(8):52-54.

Yuan Huiqun, Wang Zhenghao, Wen Bangchun. Analysis on stability of dual-discs rub-impact rotor with consideration of casing elasticity[J]. Journal of Vibration and Shock, 2010,29(8):52-54. (in Chinese)

[12]张娅,王维民,杨佳丽,等.不同轴承支撑下碰摩转子系统的动力学特性[J].振动、测试与诊断,2014,34(6):1115-1119.

Zhang Ya, Wang Weimin, Yang Jiali, et al. Nonlinear dynamic behavior of rub-impact rotor system supported by different types of bearings[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(6):1115-1119. (in Chinese)

[13]赵广,刘占生,叶建槐,等.转子-不对中花键联轴器系统动力学特性研究[J].振动与冲击,2009,28(3):78-82.

Zhao Guang, Liu Zhansheng, Ye Jianhuai, et al. Dynamic behavior of a rotor-misaligned spline coupling system[J]. Journal of Vibration and Shock, 2009,28(3):78-82. (in Chinese)

[14]闻邦椿,顾家柳,夏松波，等.高等转子动力学[M].北京：机械工业出版社,2000:124-134.

[15]Harsha S P. Nonlinear dynamic response of a balanced rotor supported by rolling element bearings due to radial internal clearance effect[J]. Mechanism and Machine Theory, 2006,41(6):688-706.

[16]Chen Guo. A new rotor-ball bearing-stator coupling dynamics model for whole aero-engine vibration[J]. Journal of Vibration and Acoustics, 2009,131(6):1980-1998.

[17]成枚,孟光.含Alford力的非线性转子-滚动轴承系统动力分析[J]. 中国机械工程, 2011,22(23):2806-2812.

Cheng Mei, Meng Guang. Dynamic analysis of a rotor-ball bearing nonlinear system with Alford force[J]. China Mechanical Engineering, 2011,22(23):2806-2812. (in Chinese)

[18]桑潇潇，廖明夫，李为.故障转子挤压油膜阻尼器减振特性试验[J].振动、测试与诊断,2015,35(5):978-981.

Sang Xiaoxiao, Liao Mingfu, Li Wei. Experimental study on the damping performance of squeeze film damper in rotor with faults[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(5):978-981. (in Chinese)