直动式溢流阀的分岔分析与实验*

2016-11-23周志鸿耿晓光

振动、测试与诊断 2016年3期

关键词：阀座油液液压

马威，马飞，周志鸿，耿晓光

(北京科技大学机械工程学院北京, 100083)

直动式溢流阀的分岔分析与实验*

马威，马飞，周志鸿，耿晓光

(北京科技大学机械工程学院北京, 100083)

为了改善广泛应用的直动式溢流阀的颤振行为，考虑油液压缩性、管道弹性和阀芯碰撞阀座时的能量损失，建立了溢流阀无量纲形式的数学模型。以4种不同的弹簧预压缩量，作出了相位和向量场分布图，得到了系统的稳定平衡状态。应用非光滑动态系统理论和计算软件MATLAB，画出了单参数和双参数分岔图，发现系统存在Hopf分岔、极限环鞍结点分岔、广义Hopf分岔和尖点分岔等分岔现象。搭建了测试平台，得到了阀芯位移分岔图和频谱瀑布图，对数学模型进行了实验验证。结果表明，小流量时为混沌或周期碰撞震荡，增大流量可改善阀芯颤振行为，为周期非碰撞震荡或稳定平衡状态。此研究工作为直动式溢流阀的失稳机理和颤振行为提供了理论依据。

溢流阀； Hopf分岔；极限环鞍结点分岔；广义Hopf分岔；尖点分岔

引言

直动式溢流阀是液压系统中不可或缺的压力控制元件，用来防止系统压力过载，然而因为复杂的流固耦合作用，溢流阀往往会趋于失稳并发生自激振荡的现象。溢流阀稳定性理论分析研究取得了大量成果。张怀亮等[1]建立了溢流阀的Simulink仿真模型，分析了基础振动及结构参数对溢流阀动态特性的影响规律，发现调定压力波动幅值随基础振动的振幅增大而线性增大。刘银水等[2]针对海水液压介质的特点，设计了一种直动式水压溢流阀，在仿真分析的基础上, 得到阀的主要结构参数即介质、运动质量、阻尼以及管路容积对阀动态响应特性的影响。吴珊等[3]采用现代控制方法获得了溢流阀的状态方程，并结合工程控制理论获得传递函数模型，采用Routh稳定性判据对阀的稳定性做出了判定，并进行了相对稳定性分析，通过仿真分析获得了该阀的动态特性曲线以及上升时间等动态特性参数，同时对阀在脉动流量输入条件下的动态性能进行了仿真。张天霄等[4]应用振动理论对液压冲击情况下的液压溢流阀进行了振动分析，建立了溢流阀的振动模型，研究了溢流阀的固有频率和瞬态响应问题，并进行了仿真验证。Eyres[5]建立了具有线性弹簧和非线性阻尼的溢流阀的闭环回路系统，用非光滑数值延拓法来跟踪稳定和不稳定解，发现阀芯与阀座的碰撞导致擦边分岔，另外，用数值仿真提出了不变环面的擦边现象。Izuchi[6]发现溢流阀的动态失稳由阀芯运动和入口管内压力波交互作用产生，延长入口管长度可减小阀芯的震荡运动，通过数值仿真预测了入口管长度和出口区面积对溢流阀稳定性的影响。Li[7]建立了三维可压缩湍流模型，用于获取流量和温度场，通过有限体积法来解流动和传热控制方程，结果表明，随着阀门开度的增大，油液作用于阀芯上的轴向力先是减小然后增大。

得益于计算流体动力学(computational fluid dynamics，简称CFD)的发展，一些研究成果采用了先进的CFD解算器。陈青等[8]应用软件Fluent,对三级同心溢流阀模型的多种工况进行了仿真计算和可视化研究，给出了锥阀阀腔内的速度场、压力场分布图。Srikanth等[9]对回路紧急切断阀进行了移动网格化的二维流量分析。在溢流阀稳定性相关的实验研究工作中，杨忠炯等[10]建立了溢流阀在强振动环境下的动力学仿真模型，结果表明，当系统稳定时，系统会衰减振动至稳定，但当干扰幅值超过临界值时，系统会进入极限环的吸引域，产生周期性振动，通过增加阀口直径、弹簧刚度和减小阀芯半锥角，可增强溢流阀的抗干扰能力。

针对以上溢流阀颤振相关的实验研究工作的不足，笔者首先分析了液压回路中溢流阀的结构特点，考虑油液压缩性、管道弹性和阀芯碰撞阀座时的能量损失，建立了溢流阀的无量纲动力学数学模型；然后，分别设定4种开启压力，得到不同初值在时间序列上的阀芯运动轨迹，应用非光滑动态系统理论，画出单参数和双参数分岔图，理论分析Hopf分岔、极限环鞍结点分岔、广义Hopf分岔和尖点分岔等分岔现象；最后，通过动态测试，对数学模型的正确性和分岔分析的可行性进行了验证。

1 数学模型

图1描述了系统结构[11]。液压油由动力部分提供，包括齿轮泵和附加安全阀用于保护系统，动力部分提供给系统流量Qpump。然而，由于液压油的压缩性和管道的弹性，进入溢流阀的流量和从泵流出的并不同。为了模拟压缩效应，增加了一个假设的腔室，其体积等于系统中的油液体积，这个腔室代表着系统的刚度。

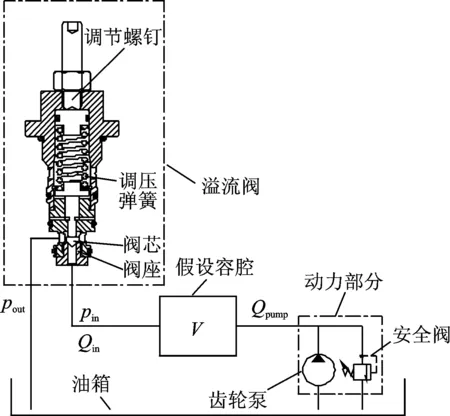
图1 液压系统结构图Fig.1 Schematic diagram of hydraulic system

腔室的质量守恒公式如下

(1)

其中：ρ为液压油密度(一般来说，液压油的密度随温度的升高而略有减小，为了简化建模过程，文中假设其为常量)；V为系统油液总体积；Qpump为泵出口流量；Qin为进入溢流阀的流量[12]。

(2)

(3)

其中：pvalve为溢流阀两侧的压差；pin为溢流阀入口压力；pout为溢流阀出口背压。

假设阀芯部分开启，阀芯和阀座之间的通流面积由图2中的垂直距离h得到

其中：通流直径d和阀座孔径D由图2定义；α为半锥角。

通过h=xsinα替代，最终得到

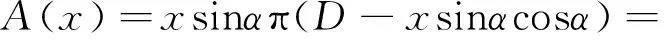
(4)

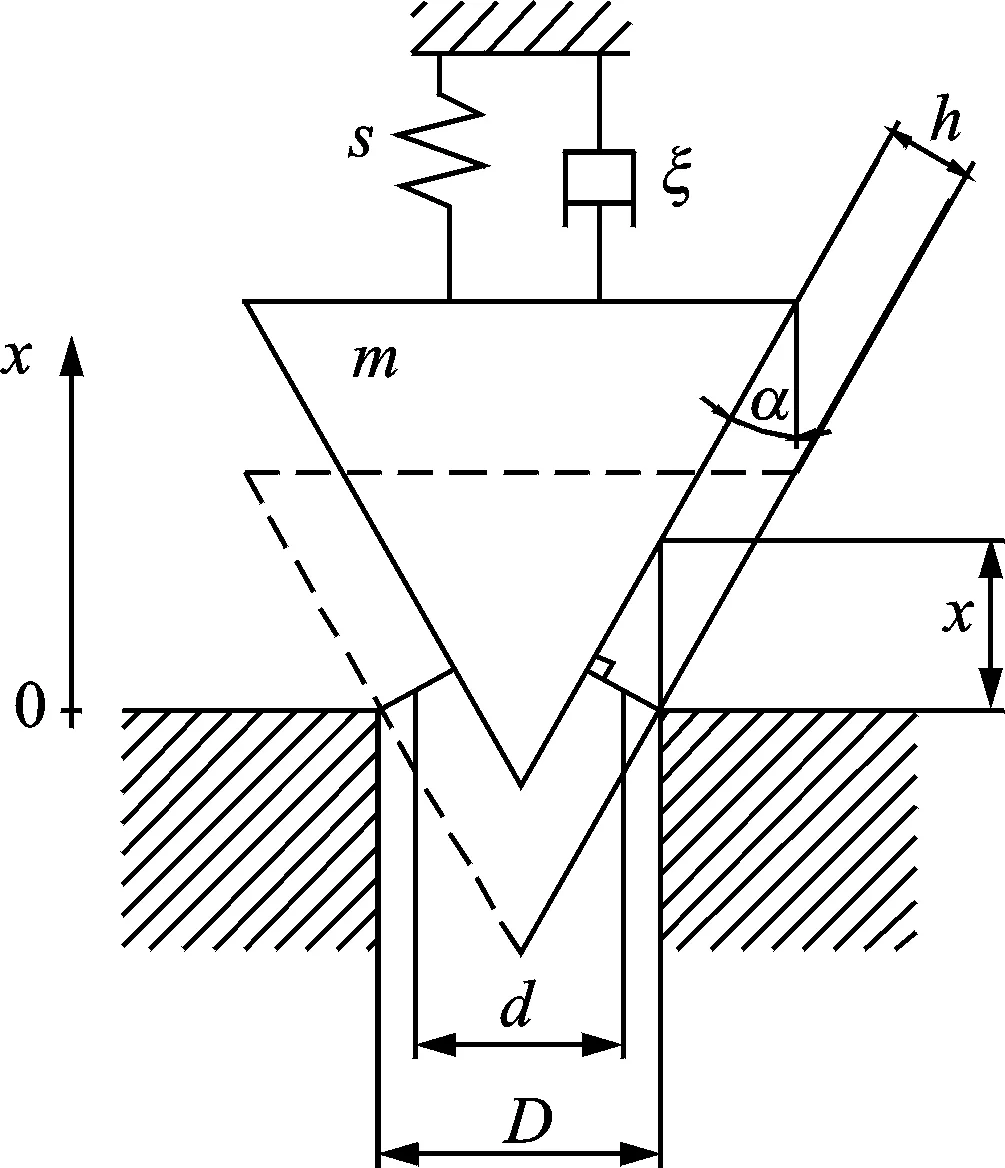
图2 阀结构Fig.2 Geometry of the valve

根据图2中的阀结构，并假设油液是正压的，也就是它的密度只取决于压力，式的左侧可写成

阀芯的动力学用牛顿第二定律描述，结合碰撞恢复系数r用来描述碰撞之后的能量损失。系统行为用常微分方程表示如下

(5)

(6)

其中：x和v分别为阀芯的位移和速度；ξ为阻尼系数；s为弹簧刚度；m为移动部分质量；x0为弹簧预压缩量；A为系统压力作用于阀芯底部的面积；pvalve为溢流阀两侧的压差；E为考虑油液压缩性和油管弹性之后的系统等效弹性模量；Qpump为泵出口压力；V为系统全部油液体积；Cd为阀入口处的流量系数；A(x)为阀芯部分开启时的有效通流面积；ρ为液压油密度。

式(4)中表达的A(x)非常复杂，将它线性化并写成A(x) =c1x，其中c1=sinαπD为线性系数，描述了通流面积和阀芯位移之间的线性关系。因为实验中阀芯位移极小，可以认为线性化非常精确地描述了实际情况。

式(6)表示一次碰撞，v-为碰撞前的速度，v+为碰撞后的速度，r为碰撞恢复系数。

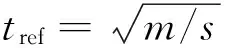
式(4)可写成无量纲形式

(7)

(8)

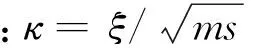
表1为实验室测得的溢流阀物理参数，用于计算无量纲参数，当开启压力popening= 1 MPa，得到κ= 1.23，β= 17.57，δ= 22.67。

表1 溢流阀物理参数

2 分岔分析

无量纲流量q是最容易改变的参数。首先，利用MATLAB软件画出以q作为自由参数的单参数分岔图；其次,溢流阀的预设压力也容易改变，无量纲预压缩参数δ决定着阀的开启压力，因此通过同时改变q和δ得到双参数分岔图，揭示溢流阀的震荡特性。

2.1 相位和向量场分布图

改变无量纲预压缩参数δ的值，即调节溢流阀的设定值，可得到不同初值在时间序列上的阀芯运动轨迹，如图3所示。

图3 δ分别为40，30，20和10时，时间序列上的阀芯运动轨迹Fig.3 Trajectories of valve poppet time history for δ = 40, 30, 20, 10

取不同的初值，不考虑瞬态的影响，在时间足够长的情况下，由图4(a)可知，当δ= 40时，阀芯将最终稳定在y1= 8.606，或者周期震荡；由图4(b)可知，当δ= 30时，阀芯将以两个振幅做周期震荡；由图4(c)可知，当δ= 20时，阀芯将最终稳定在y1= 10.81；由图4(d)可知，当δ= 10时，阀芯将最终稳定在y1= 12.616。

图4 相位和向量场分布图 Fig.4 Phase and vector field diagrams

2.2 Hopf分岔

为了画出分岔图，以q作为自由参数，对于每一个q值以一系列不同的初始条件运行仿真，记录下瞬变消失后的点。选择平面y2= 0作为三维相空间的二维Poincare截面。

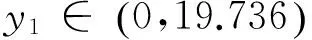
图5 δ = 22.67时单参数分岔图Fig.5 Bifurcation diagram for δ = 22.67

下面理论验证Hopf分岔点。当q= 26时，考察系统(7)的平衡点

(9)

线性化系统得雅克比矩阵为

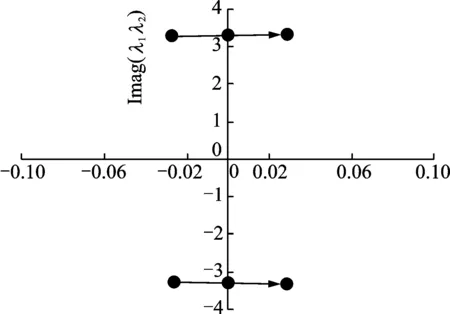
图6 复平面内特征值λ1，λ2的运动轨迹Fig.6 The trajectories of eigenvalues λ1 and λ2 on complex plane

2.3 极限环鞍结点分岔

图7 δ = 40时的单参数分岔图Fig.7 Bifurcation diagram for δ = 40

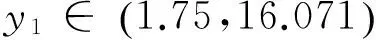
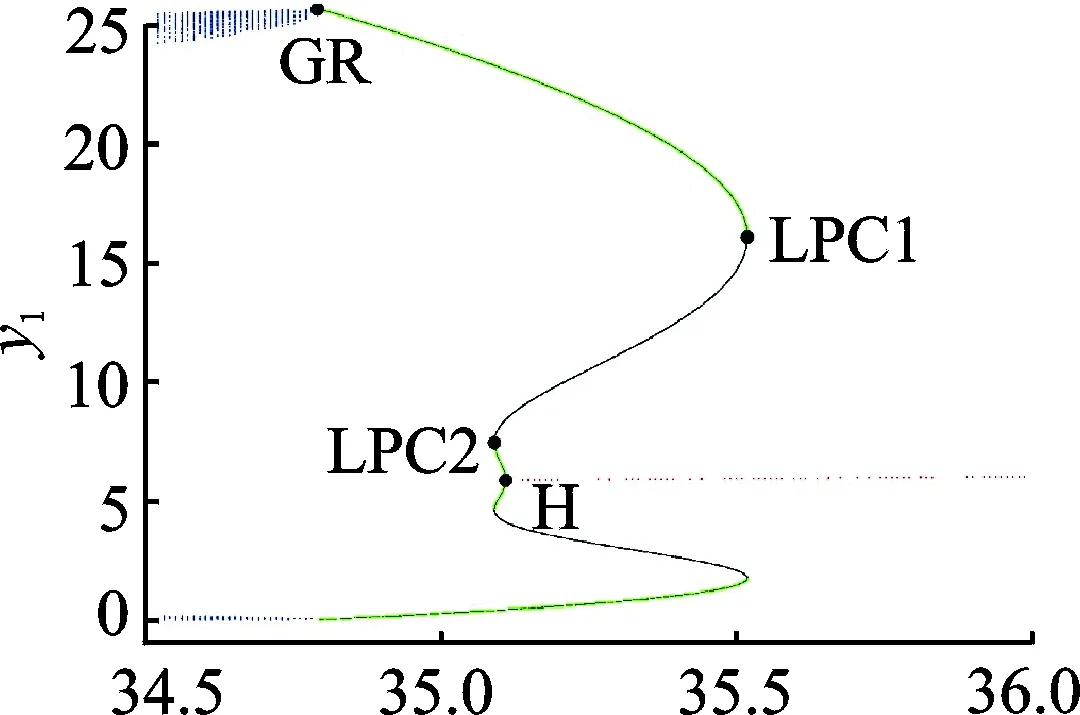
图8 δ = 30时的单参数分岔图Fig.8 Bifurcation diagram for δ = 30

2.4 广义Hopf分岔

图9所示为双参数分岔图，H表示Hopf分岔曲线，LPC1和LPC2表示极限环鞍结点分岔曲线，CPC表示尖点分岔，GH表示广义Hopf分岔。LPC1与H相交于GH点，坐标为(q，δ) = (28.493,25.262)；LPC1与LPC2相切于CPC点，坐标为(q，δ) = (25.065，22.831)。

图9 双参数分岔图Fig.9 Two-parameter bifurcation diagram

图10所示为广义Hopf分岔(GH)示意图，LPC1与H分岔曲线将参数平面分为4个区域，按逆时针方向排列分别为(1),(2),(3),(4)。区域(1)有1个稳定平衡点、1个稳定极限环和1个不稳定极限环；区域(2)有1个不稳定平衡点；区域(3)和(4)有1个稳定平衡点。

图10 广义Hopf分岔(GH)示意图Fig.10 Qualitative diagram for generalized Hopf bifurcation(GH)

2.5 尖点分岔

如图11所示的尖点分岔(CPC)示意图，LPC1与LPC2分岔曲线以“楔形”将参数平面分为两个部分。在区域(1)，“楔形”内有3个平衡点，2个稳定，1个不稳定；在区域(2)，“楔形”外有1个稳定平衡点。

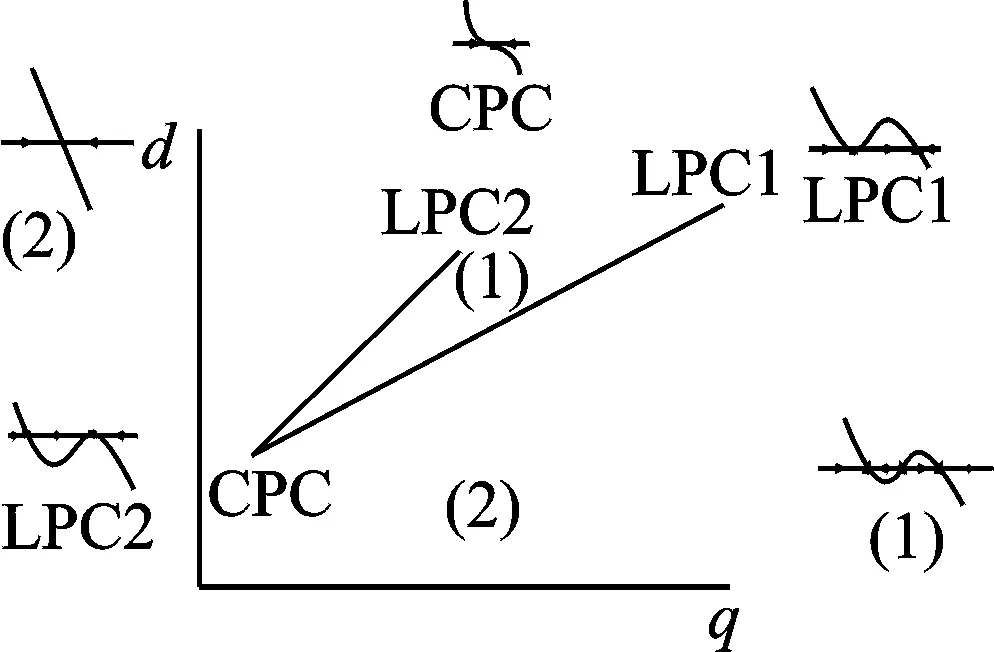
图11 尖点分岔(CPC)示意图Fig.11 Qualitative diagram for cusp bifurcation of cycles (CPC)

3 动态测试

为了验证动力学模型的正确性，搭建测试平台如图12所示。动力部分由电机1和泵2提供，安全阀3用来防止系统过载，压力传感器5、流量传感器6和阀芯位移传感器8输出信号进入数据采集仪9，由计算机10显示和存储。动态测试在预设压力popening= 1 MPa(弹簧预压缩量x0= 5 mm)下进行。从低流量开始，通过比例调速阀4逐步增大到最大流量(约120 L/min)，记录30组泵出口流量Qpump情况下的溢流阀入口压力pin和阀芯位移x。

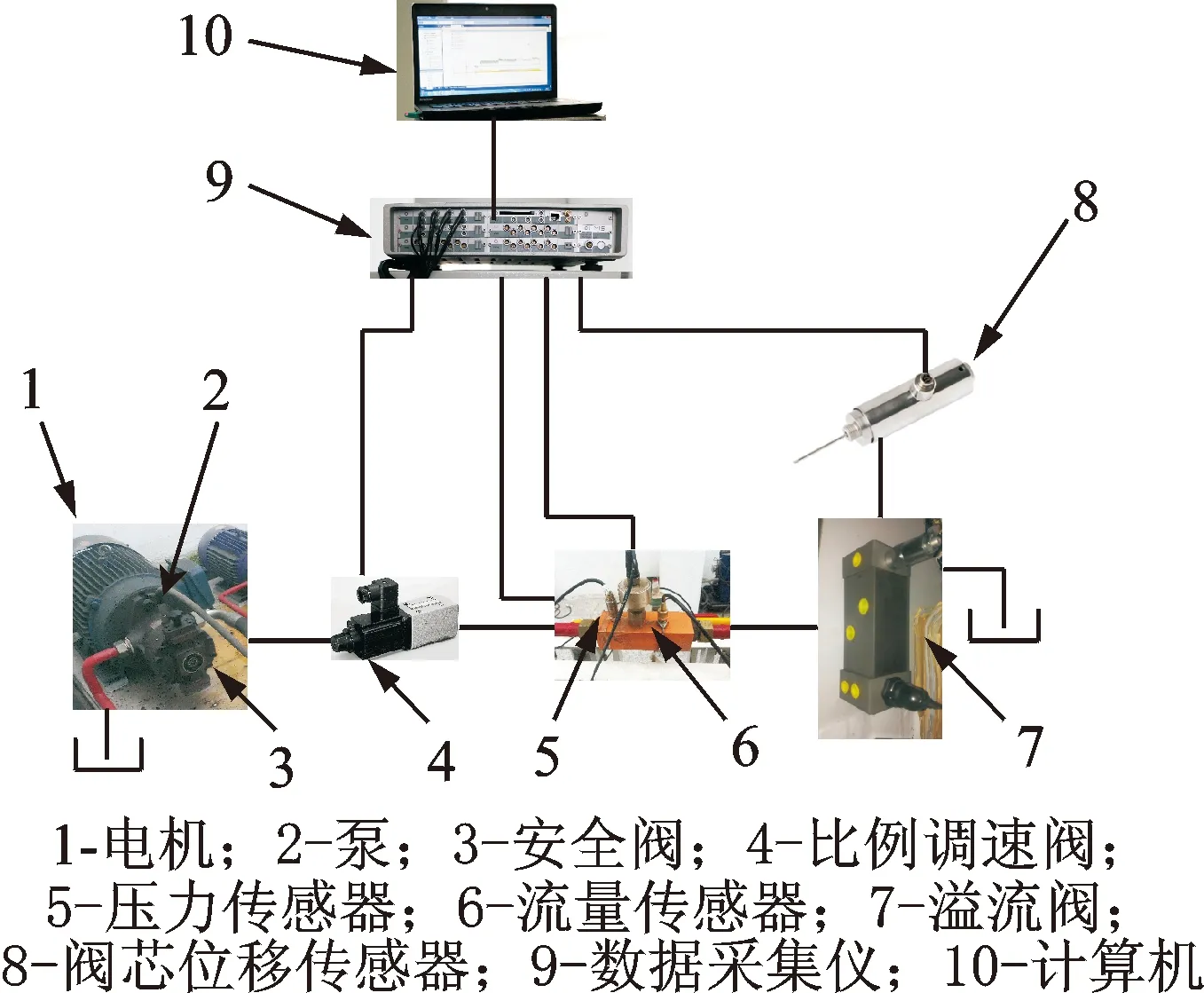
图12 测试平台Fig.12 Test platform

图13 缓慢改变流量的测试分岔图Fig.13 Measured bifurcation diagram of the system while slowly varying the flow rate

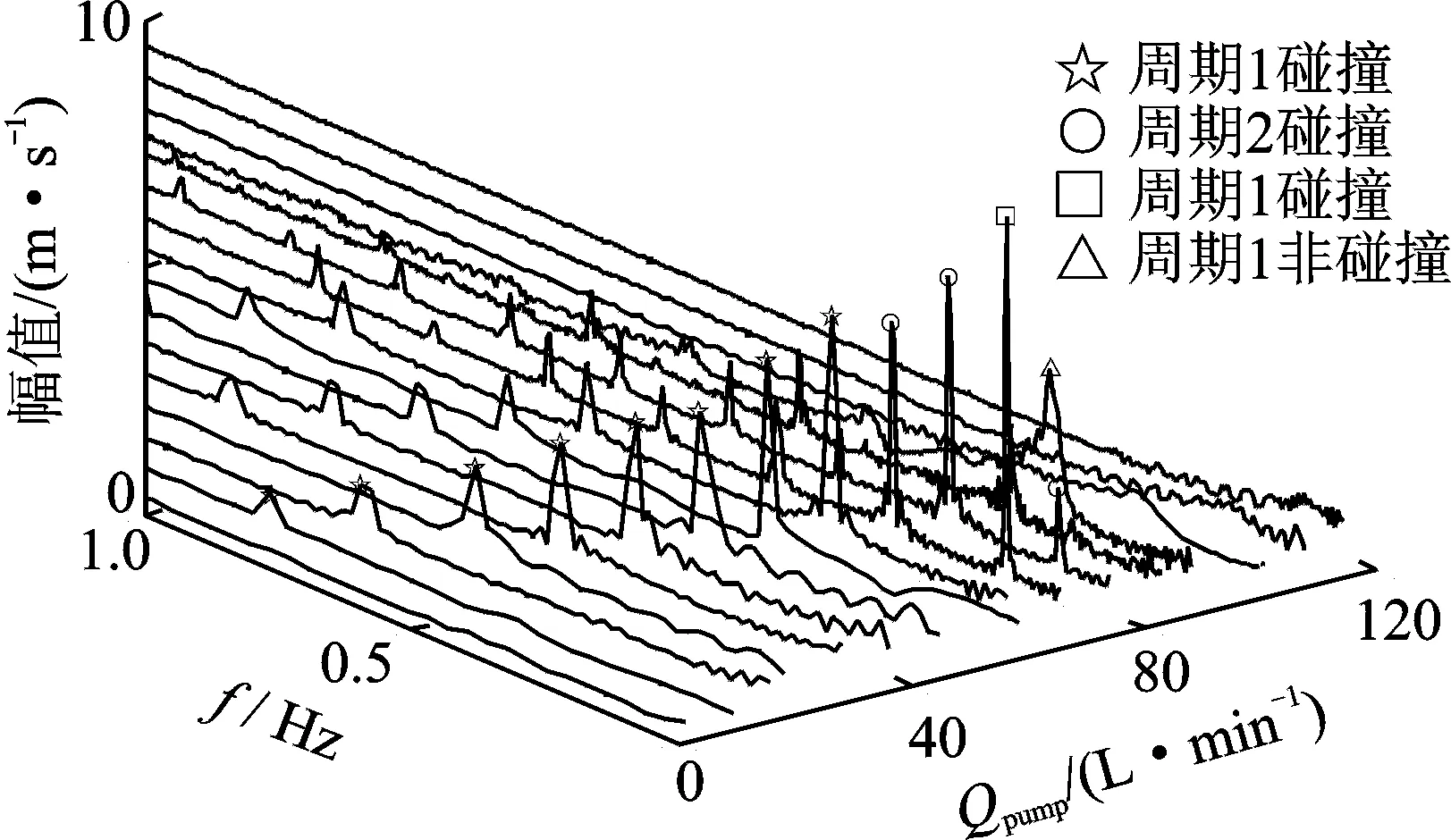
图14 频谱瀑布图Fig.14 Waterfall diagram for the spectra

图13为缓慢改变泵出口流量Qpump的测试分岔图。图14为溢流阀阀芯振动幅值随泵出口流量Qpump变化的频谱瀑布图。图15(a)～(d)为4个典型的阀芯时间序列上的位移和频谱图。

从图13和图14可以看出，流量极小时，阀芯是不稳定的，呈现出混沌碰撞震荡的运动形式，典型轨迹如图15(a)所示(Qpump=8 L/min)；增大流量，振荡幅值和周期逐渐增大，典型轨迹如图15(b)所示(Qpump=40 L/min)，基频fm=0.585 4 Hz；流量达到95 L/min，即擦边分岔，阀芯离开阀座，非碰撞周期振荡开始，典型轨迹如图15(c)所示(Qpump=100 L/min)，基频fm=0.396 2 Hz；增大流量，振荡幅值开始减小，在临界值102 L/min之后，阀芯处于稳态平衡，典型轨迹如图15(d)所示(Qpump=108 L/min)。

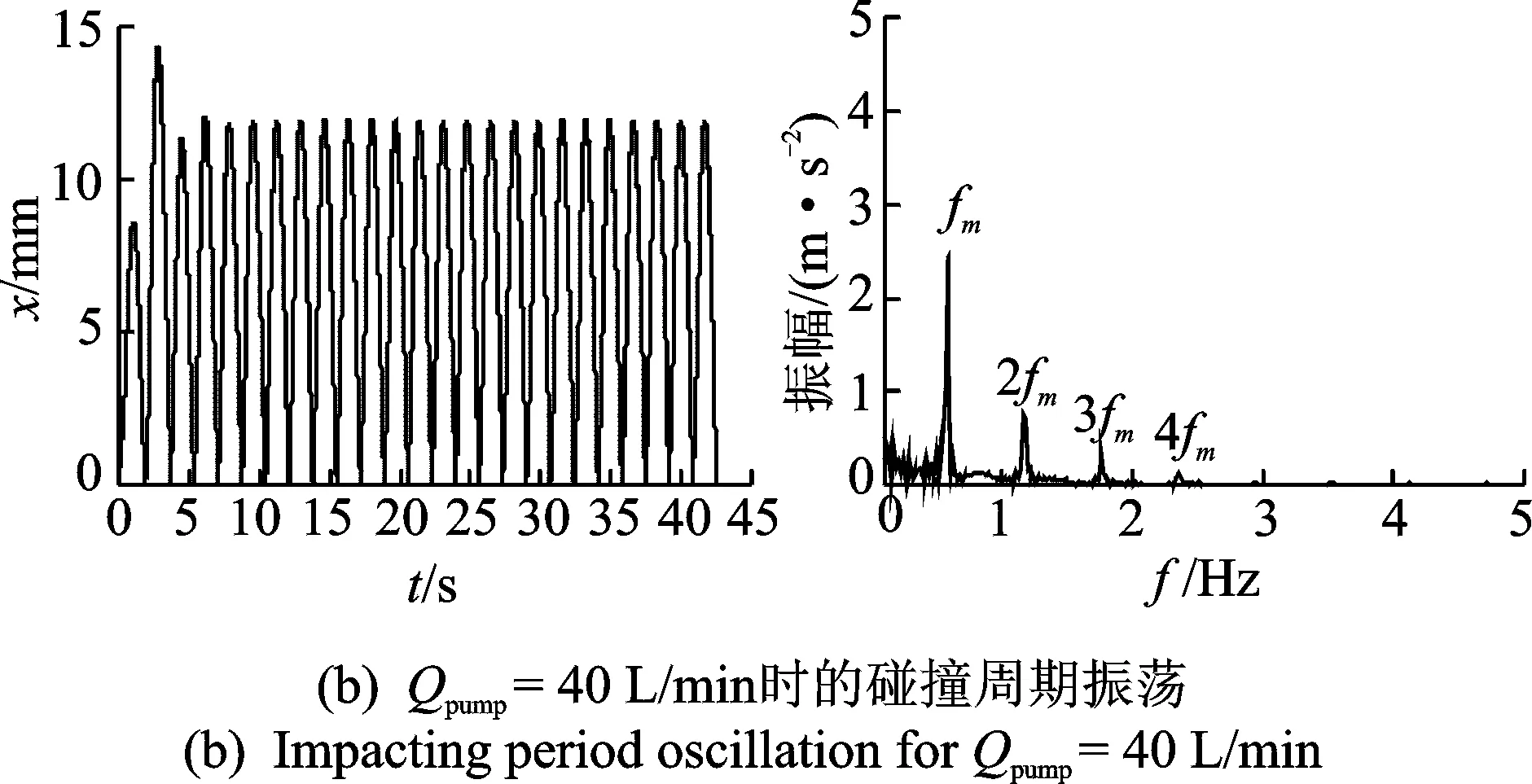
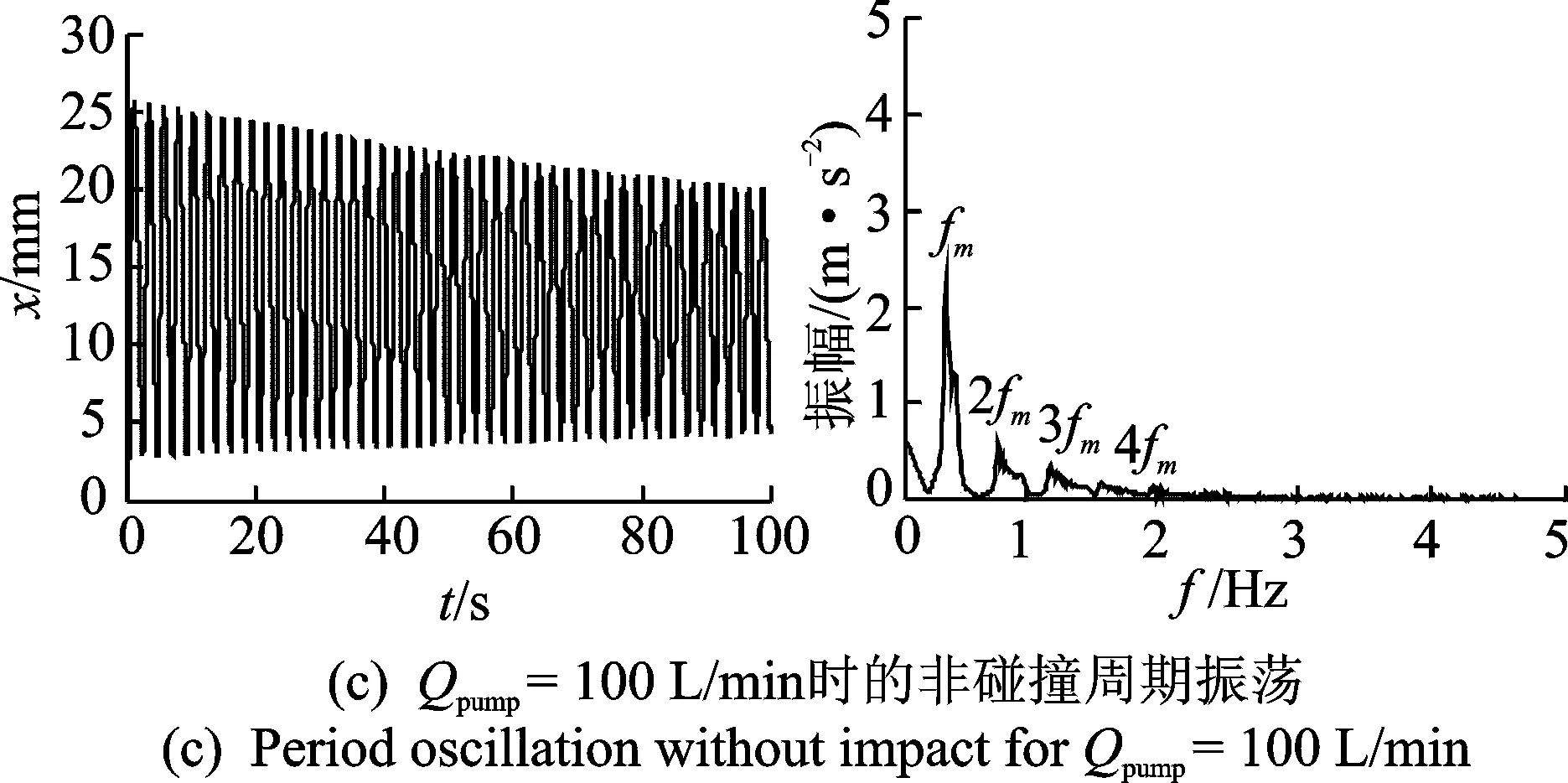
图15 阀芯时间序列上的位移和频谱图Fig.15 Displacement time histories and spectrum diagram

4 结束语

1) 建立了溢流阀的数学模型，以不同的预压缩参数δ作出系统相位和向量场分布图，通过以q作为自由参数作出单参数分岔图，发现了Hopf分岔，并进行了理论验证。

2) 当δ= 40和30时，出现了极限环鞍结点分岔现象。同时改变q和δ得到了双参数分岔图，分析了广义Hopf分岔和尖点分岔对参数平面区域的划分。

3) 实验证明，小流量时阀芯是不稳定的，呈现出混沌的运动形式。增大流量到20 L/min，系统进入周期性碰撞运动；直到95 L/min，当阀芯离开阀座，擦边分岔之后，非碰撞周期振荡开始；102 L/min之后，Hopf分岔出现，阀芯变得稳定。

[1] 张怀亮，章国亮，齐征宇．基础振动下直动式溢流阀的动态特性[J]．中南大学学报:自然科学版，2014，45(12)：4181-4186．

Zhang Huailiang, Zhang Guoliang, Qi Zhengyu. Dynamic characteristics of direct operated relief valve on fundamental vibration[J]. Journal of Central South University:Science and Technology,2014，45(12):4181-4186. (in Chinese)

[2] 刘银水，毛旭耀，吴德发，等．直动式海水液压溢流阀的设计与仿真[J]．华中科技大学学报:自然科学版，2010，38(9)：125-128．

Liu Yinshui, Mao Xuyao, Wu Defa,et al. Design and simulation of a seawater hydraulic relief valve[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2010, 38(9): 125-128. (in Chinese)

[3] 吴珊，毛旭耀，吴德发．直动式海水液压溢流阀的稳定性能分析[J]．华中科技大学学报:自然科学版，2010，38(10)：89-92．

Wu Shan, Mao Xuyao, Wu Defa. Stability analysis of a direct-acting seawater hydraulic relief valve[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2010, 38(10): 89-92. (in Chinese)

[4] 张天霄，刘昕晖，张农. 液压溢流阀的振动分析[J]. 吉林大学学报：工学版，2014，44(1)：91-94.

Zhang Tianxiao, Liu Xinhui, Zhang Nong. Vibration analysis of hydraulic relief valve[J]. Journal of Jilin University: Engineering and Technology Edition, 2014, 44(1): 91-94.(in Chinese)

[5] Eyres R. Grazing bifurcations and chaos in the dynamics of a hydraulic damper with relief valves[J]. SIAM Journal on Applied Dynamical Systems, 2005, 4(4): 1076-1106.

[6] Izuchi H. Stability analysis of safety valve[C]∥10th Topical Conference on Gas Utilization. San Antonio, Texas:American Institute of Chemical Engineers,2010.

[7] Li Defu, Xia Xinlin, Dai Guilong, et al. Numerical Simulation on Fluid Dynamic Behavior of High-pressure Safety Valves[C]∥Power and Energy Engineering Conference (APPEEC), 2010 Asia-Pacific.Chengdu: IEEE, 2010.

[8] 陈青，许惠，权龙．三级同心液压溢流阀噪声特性的CFD分析[J]．振动、测试与诊断，2009，29(1)：71-74．

Chen Qing, Xu Hui, Quan Long. CFD simulation of noise characteristic of coaxial hydraulic relief valve with three stages[J]. Journal of Vibration, Measurement & Diagnosis, 2009, 29(1): 71-74. (in Chinese)

[9] Srikanth C, Bhasker C, Flow analysis in valve with moving grids through CFD techniques[J]. Advances in Engineering Software, 2009, 40(3): 193-201.

[10]杨忠炯，李洪宾，周立强，等．强冲击下先导式溢流阀先导阀芯自激振动仿真[J]．华中科技大学学报:自然科学版，2015，43(4)：58-63.

Yang Zhongjiong, Li Hongbin, Zhou Liqiang, et al. Simulation of self-excited vibration behavior of pilot valve core on pilot-operated pressure relief valve with strong vibration[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2015,43(4):58-63.(in Chinese)

[11]Licskó G, Champneys A, Hös C. Nonlinear analysis of a single stage pressure relief valve[J]. International Journal of Applied Mathematics, 2009, 39(4): 12-25.

[12]Hussain S, Hussain A, Ahmad Z. Discharge characteristics of orifice spillway under oblique approach flow[J]. Flow Measurement and Instrumentation, 2014. 39(10): 9-18.

[13]Li Yan. Hopf bifurcations in general systems of Brusselator type[J]. Nonlinear Analysis: Real World Applications, 2016, 28: 32-47.