直升机振动检测通用算法的研究与实现*

2016-11-23龙海军孙灿飞莫固良

振动、测试与诊断 2016年3期

关键词：傅里叶旋翼时域

龙海军 , 孙灿飞, 莫固良

(1.中航工业故障诊断与健康管理航空科技重点实验室上海, 201601)(2.中航工业上海航空测控技术研究所上海, 201601)

直升机振动检测通用算法的研究与实现*

龙海军1,2, 孙灿飞1,2, 莫固良1,2

(1.中航工业故障诊断与健康管理航空科技重点实验室上海, 201601)(2.中航工业上海航空测控技术研究所上海, 201601)

针对国内现有振动检测设备在直升机振动噪声测量领域的可靠性影响到维护效率及急待提高国内直升机振动检测设备性能问题，首先，对多种直升机振动噪声进行了研究与分析；其次，针对直升机噪声的复杂性详细阐述了信号的预处理方法；最后，提出了适合直升机振动噪声自适应整周期采样时域同步平均-短时傅里叶变换方法。现场验证比较结果表明，整周期采样时域同步平均-短时傅里叶变换测量方法在直升机振动测量中优于其他振动算法，自适应调整能力强，信号的优劣程度对测量结果影响小，分析更加准确，实时性得到了改善。此方法同样适用于其他转子振动测量领域。

振动测量；整周期采样；时域同步平均；短时傅里叶变换

引言

直升机具有灵活方便的使用特点，在军事及民用中发挥着越来越重要的作用，但是直升机较高的噪声却一直制约着直升机大规模使用，噪声大不仅会造成机械结构的疲劳度，缩短飞机的使用寿命，而且使得空勤人员的执行效率降低和仪表设备失效等，严重时危及到机组人员的生命安全。直升机振动噪声主要来源于主旋翼和尾桨噪声，因此，噪声测量的准确度成为直升机维护的重要纽带，关系到维护人员的维修效率。当代直升机的振动水平已降到0.1g左右，尤其美国对新型直升机提出的振动水平要求更加严格(相当于0.05g的水平)，这对直升机振动检测[1-3]设备提出了更高的检测要求。国内现有直升机振动检测设备测量准确度有待改善，尤其是小信号的测量精度问题更加突出，主流产品还是国外的振动检测设备。

近年来国外直升机振动检测设备主要有美国霍尼韦尔和ACES，国内的直升机振动检测设备研发投入比较少，功能、性能与国外产品相比还有不少差距，主要体现在研发人员对直升机振动信号的整体理解与算法[4-5]的研究方面。究其原因：a.由于直升机上不同的振源、不同的频率及不规则的作用使得振动分析非常复杂，国内对直升机的振动理论探讨较少；b.直升机由于其动力源和结构上的特点，使机体始终处于主旋翼和尾桨为主的强干扰源下作强迫振动。其振动特点是：随机信号上叠加其他几个强正弦信号，正弦信号的幅值又带有随机性；干扰频率成分较复杂且主干扰源的频率较低；机体刚体姿态频率很低。这些特点决定现有的国内振动检测设备直接用频域傅里叶变换或时域的处理方法难以达到理想的测量效果。

为了解决国内现有直升机振动检测设备算法的缺陷，通过对多种直升机主旋翼、尾桨振动噪声的分析和多种测量方法的研究类比，提出了整周期采样时域同步平均-短时傅里叶变换[6-8]测量算法。经现场验证表明，此算法自适应调整能力强，信号的优劣程度对测量结果影响小，分析更加准确，可靠性、实时性得到了改善。

1 振动噪声特征与测量方法

直升机由于其动力源和结构的特点，使机体始终处于主旋翼和尾桨为主的强干扰源下作强迫振动。旋翼和尾桨噪声是现代直升机最主要的噪声来源。

旋翼噪声是直升机飞行时的主要噪声。研究表明,当直升机飞行时，它的谱呈线谱特征，主要取决于旋翼的工作状态，与飞行方向关系不大，旋翼围绕其顶轴匀速运动，周期性地拍打空气，引起空气有规则的脉动，所产生的噪声频率为f=nzm/60，其中:n为旋翼转速;z为旋翼叶片数。直升机具有稳定的基频，在飞行情况下还要产生一个多普勒频移Δf，其计算公式为Δf=Fbvcosφ/c，其中：Fb为基频；v为直升机水平飞行速度；c为声在空气中的传播速度；φ为直升机飞行速度方向与直升机到测点连线之间的夹角。经过对各种直升机的计算分析发现，f<2 Hz，多普勒频移甚低，不会改变直升机噪声的周期性和低频特性。尾桨噪声则体现在直升机起飞、爬升、大速度前飞及悬停等飞行状态，可以分为旋转噪声、宽带噪声和高速脉冲噪声。尾桨噪声是直升机重要噪声源，因为尾桨的转速较高，它的通过频率落在人的听力敏感区，引起人耳极度不适。

直升机噪声信号既有周期、慢时变成分，又有桨叶涡流的相互作用及较大的桨尖速度效应所产生的极强的非平稳信号。更严格地讲，直升机噪声信号是一个复杂的非线性过程，存在着大量的瞬态成分，具有非平稳特性。振动噪声有如下共同点：a.随机信号上叠加某几个强正弦信号，正弦信号的幅值又带有随机性；b.干扰频率成分较复杂，且主干扰的频率较低；c.机体刚体姿态频率很低。这些特点的振动给测试和处理带来了较多的困难。首先,传感器的低频性能难以得到保证，标定传感器的振动台在低频时的线性度比较差；其次，随机信号和正弦信号还存在着转换的问题，而对应频率幅值的随机性又对数据处理提出特殊要求。常用的信号分析算法如傅里叶变换在数据采样率的选取、采样时长的确定、可靠性、实时性的提高等难以达到最优化，而且当飞机状态恶劣时，算法的可靠性更不能得到保证；时域法则在有噪声干扰时，如何来正确辨别是其难点；小波分析法[9]由于分辨率存在一定的极限，在直升机振动复杂时难以达到良好的效果。笔者通过引入跟踪飞机状态及机型相关反馈状态，解决了数据采样率的选取、采样时长的确定、实时性、可靠性等问题。

2 信号提取与辨别

在工程实践中，对于直升机旋转轴承之类的振动测量，由于信号复杂，采用转速与振动信号同步跟踪来保证信号特征值的正确提取。图1为直升机主旋翼、尾桨传感器的安装图，图2为理想情况时转速与振动传感器的输出。

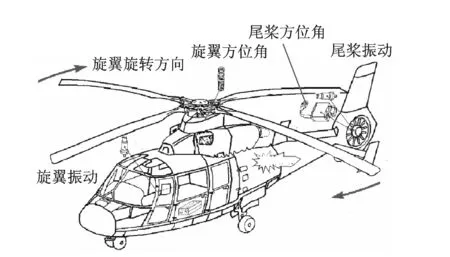
图1 直升机的传感器安装Fig.1 The installation of helicopter sensor

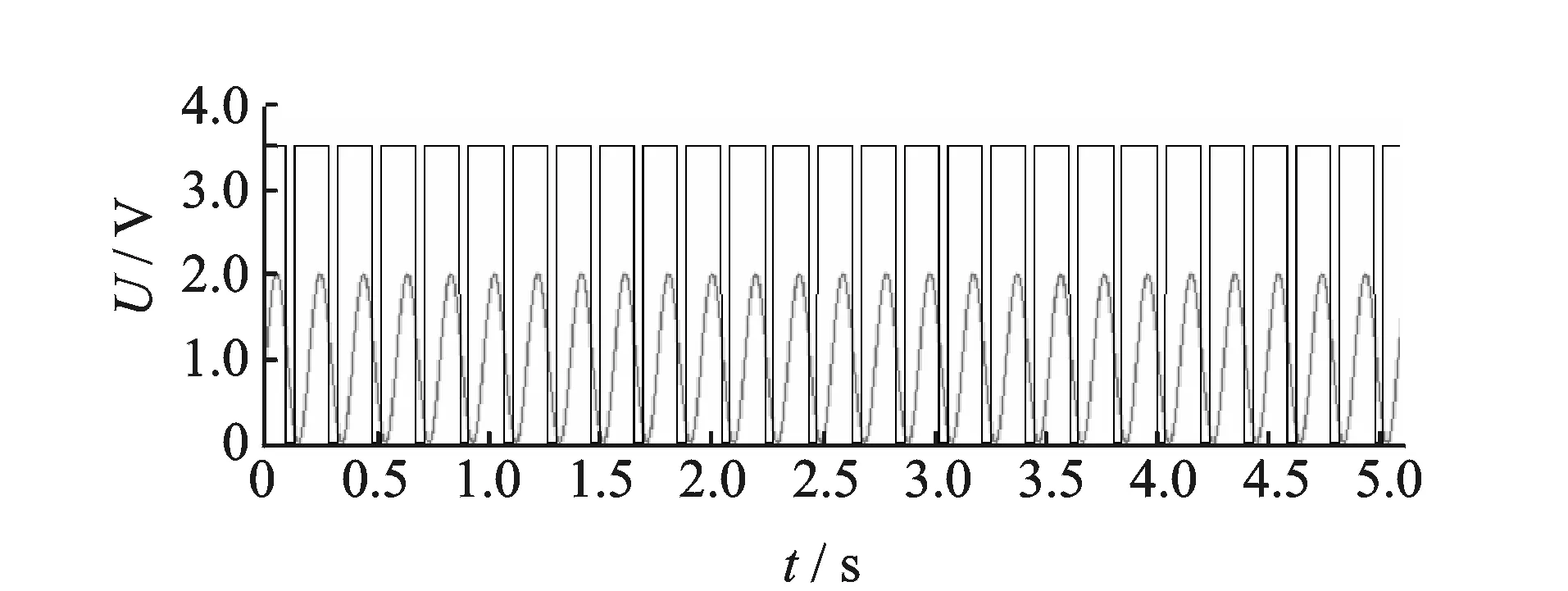
图2 转速与振动传感器的理想波形Fig.2 The ideal waveform of the speed and the vibration sensor

当旋翼与尾桨旋转时转速传感器产生方波，同时振动传感器经信调电路后输出正弦信号。主旋翼、尾桨每旋转一周，转速传感器产生一个占空比不同的方波，同时振动传感器产生相对应的正弦波，如图2所示。当转速增加时，可以看到振动信号的频率也随之增大。通过转速与振动信号相关联，就可以确定直升机振动特征值。

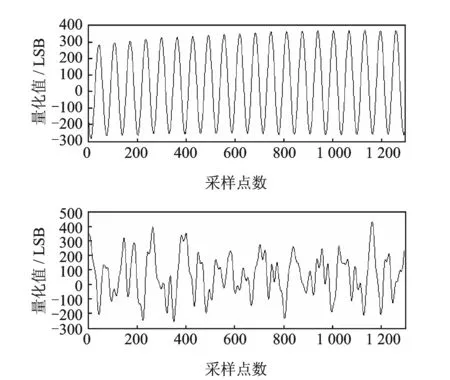
图3 直I、直II的振动信号Fig.3 The vibration signal of the helicopter with I and II

由于直升机振动信号的频率复杂，实际波形与理想波形相差悬殊，图3为两种机型的实测振动信号。其中：LSB为最低有效位。由图3上图可知，振动信号波形比较理想，但信号中夹带更低的频率分量，可以清晰地估计出待测信号的幅值和相位；下图中除了低频分量外还带有比待测信号频率高的分量，很难辨别出待测信号，需通过算法处理得出其成分。

3 时域同步平均-短时傅里叶变换

针对直升机型号不同、同型号的振动恶劣程度不一致，结合多种机型实测数据进行分析，采用图4所示的硬件方案及图5所示的软件算法。

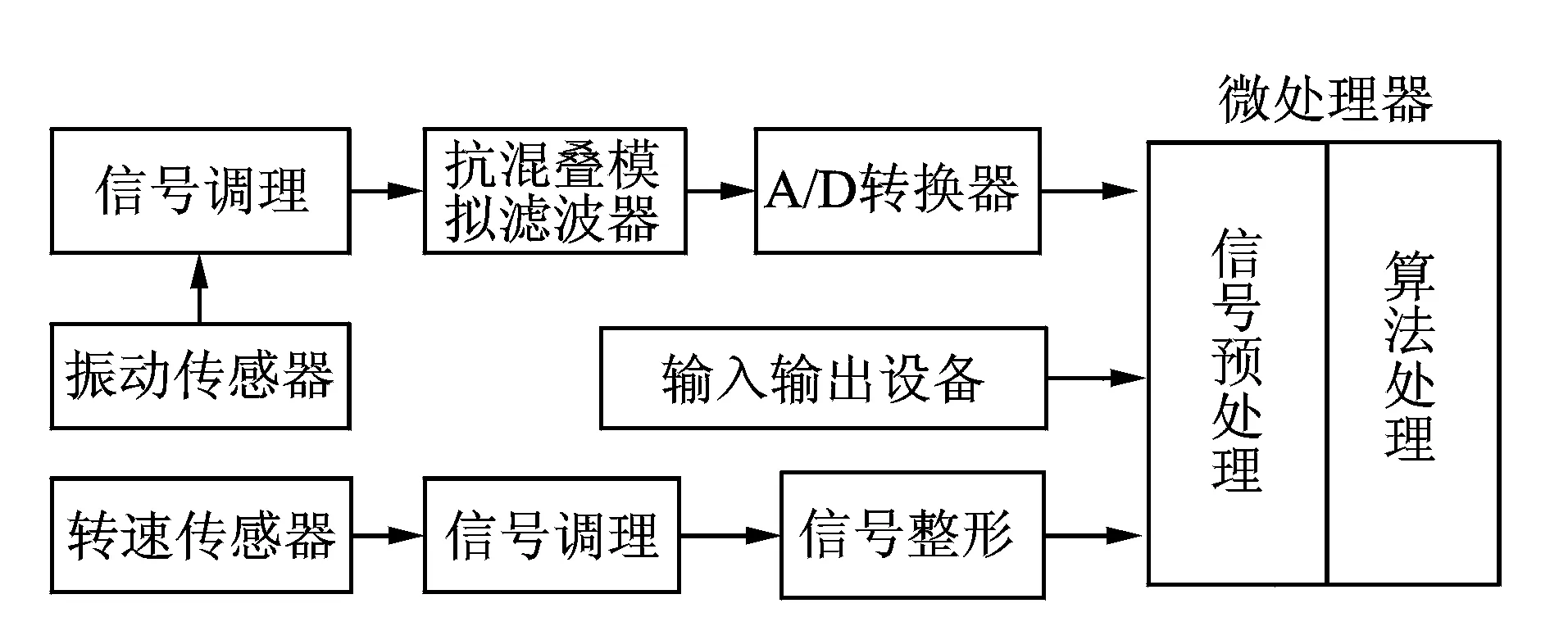
图4 硬件流程图Fig.4 The flowchart of hardware

图5 算法流程图Fig.5 The flowchart of algorithm

3.1 硬件流程

暗电流随电子辐照注量的变化关系，如图2所示。可以看出，静态辐照条件下暗电流退化比不加电辐照时退化更严重。暗电流的退化主要是由于电子辐照产生的电离损伤导致浅槽隔离(STI)界面复合电流、掩埋型光电二极管(PPD)表面缺陷复合电流、光电二极管与转移栅(TG)交叠区复合电流等三部分暗电流的增大造成的。由于10 MeV电子辐照还产生了位移损伤，因此暗电流的增大有一部分是由于体缺陷导致耗尽区载流子产生率增大所致。此外，γ射线辐照偏置效应不明显[11]，因此认为位移损伤效应表现出一定的偏置效应。

由于直升机主旋翼频率低，国内振动传感器许多参数达不到技术指标，为了满足前端信号采集要求，采用国外PCB公司的振动传感器。转速传感器则根据机型采用磁电或光电转速传感器。针对直升机振动信号经常处于振动小的状态，在信号调理时采用程控增益放大电路来满足动态测量范围要求，抗混叠滤波器设计需满足采样定理。使关系式满足 fmax≤fs/2,fmax为待测信号的最大频率，fs为信号的采样率。A/D转换器采用自带采样保持器的16位A/D转换芯片以满足测量精度要求。在转速调理电路中，针对传感器(磁电或光电转速)采用通用信调电路对磁电或光电信号进行放大，然后对波形进行整形以满足微处理器的要求。微处理器则是对振动和转速信号进行预处理、算法运算及输入输出设备响应。

3.2 算法流程

3.2.1 整周期过采样

振动信号进行傅里叶变换分析时，尽量使分析谱线落在信号的频率上以避免栅栏效应。假设振动信号为x(t)，频率为f0，采样频率为fs，采样点数为N，时间长度为T，频率采样间隔为Δf，根据傅里叶变换原理知T与Δf有如下关系

(1)

为了使分析信号落在f0处，f0与Δf须满足

(2)

其中：Z为正整数。

假设振动信号为x(t)的周期为T0，则由式(1)与式(2)得时间长度T与T0存在如下关系

(3)

采样点数为N的时间长度T与振动信号为x(t)的周期T0成正整数倍时，才能使分析谱线落在信号的频率处以获得准确频谱。因此，以待测信号的频率f为参考，采样频率动态实时跟踪信号频率，fs=n*f,n为整数，即无论频率如何变化可确保采集样点为信号周期的固定倍数，避免了频谱泄漏。如图6所示，T为信号频率，N为每个周期内的倍频脉冲数。采样过程中采用了过采样技术[10]，降低了A/D的量化噪声及抗混叠滤波器设计指标。

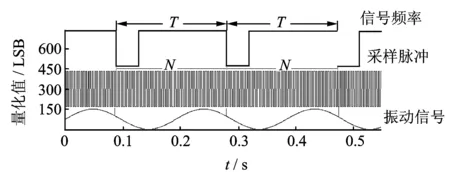
图6 整周期信号采样Fig.6 The signal sampling with whole cycle

3.2.2 信号预处理

由于振动信号优劣程度跟直升机型号、同型号维护状态存在极大关系，为了达到最优测量，在信号预处理算法中，采样一段时间振动数据进行预处理，在时域中以待测信号的转速为参考点进行多周期同步平均，根据同步平均后的数据来判断振动信号的优良程度，进而对后续的处理算法分配合理的数据采集时间和算法处理时间。多周期同步平均的转速振动信号如图7左图所示，上方为转速信号，下方为振动信号；采用每4个转速周期对振动信号进行同步平均，最终信号趋于比较理想同步平均信号，如图7右图所示。由于直升机振动分析只有在待测信号频率偏差可接受时分析的结果才有意义，因此在信号预处理中同时监测转速的稳定程度，以确定是否丢弃无效的数据进行重新采样。

时域中进行预处理算法时，假设有信号如图8所示，上方为待测信号频率，下方为混有其他干扰的待测信号。Pk为信号正峰值点，-Pk为待测信号的负峰值点，如果没有干扰信号，则4T周期内Pk总数为4，-Pk总数为4。由于干扰信号，图中Pk与-Pk远大于4。判定时域中周期信号的稳定度的必要条件是：a.NPk=N-Pk=4，N为峰值个数；b.APk/A-Pk≈1，APk为正峰值，A-Pk为负峰值。

判别时域中周期信号的稳定性，可采用4周期(实际需要)m次叠加同步平均，如图7所示。当m值增大时，信号的轮廓逐渐显现，干扰信号的峰值减小，结果如图9所示。利用峰值判定方法可容易找到信号稳定时所需的判别条件NPk=N-Pk=4，APk/A-Pk≈1，从而完成了信号的预处理。

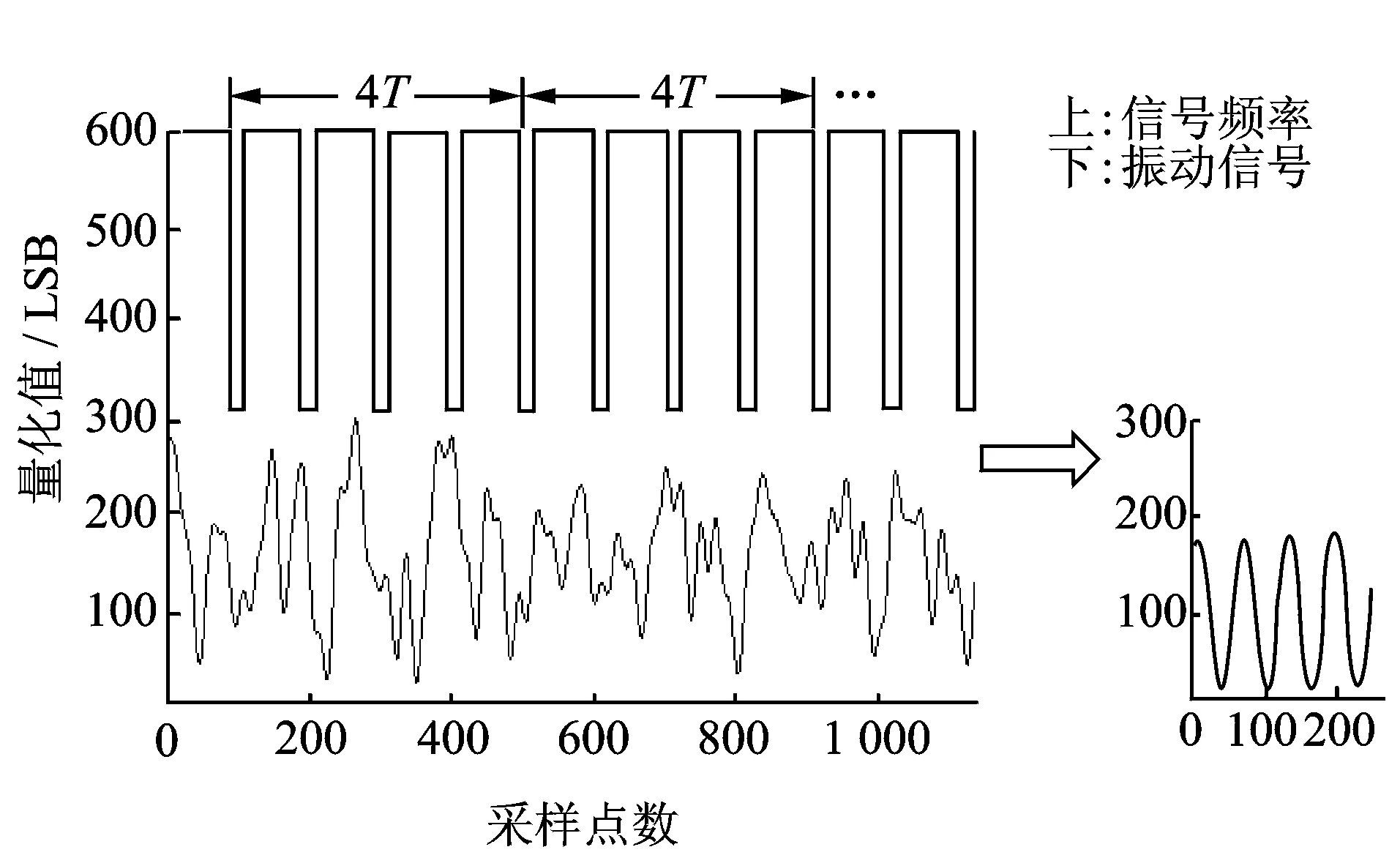
图7 振动信号预处理Fig.7 The signal preprocessing of vibration

图8 频率与振动信号Fig.8 The signal and frequency of vibration

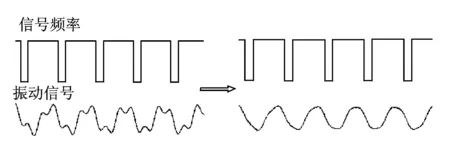
图9 预处理后的信号Fig.9 The signal preprocessed

3.2.3 短时傅里叶变换

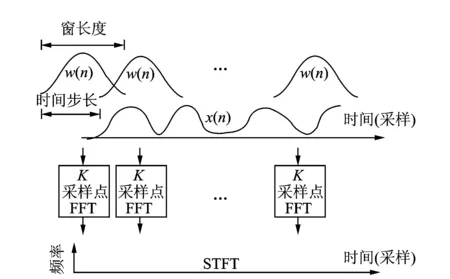
图10 短时傅里叶变换的示意图Fig.10 The schematic of STFT

K=2[ log2A],其中：A为频率区间；[]为取最近整数的运算。对于一维信号，使用快速傅里叶变换(fast Fourier transform,简称FFT)算法计算输入序列的离散傅里叶变换(discrete Fourier transform,简称DFT)。一维DFT定义如下

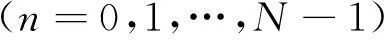
其中：x为输入序列；N为x中元素的数量；Y为变换的结果。

W(n)窗的长度可影响STFT的时间精度和频率精度。较窄的窗的持续时间较短,带宽较大，可得到更好的时间精度，但频率精度不理想。较宽的窗的持续时间较长,带宽较窄，可得到更好的频率精度，但时间精度不理想。

利用上述方法，以每4个周期对振动信号进STFT，然后将各次STFT测量结果的各个参数进行去粗大误差及求平均值，得出所需频率的幅值和相位，再对幅值和相位进行校正得出最终结果，从而确定了直升机的振动状态。

3.3 试验数据

采用傅里叶变换与文中设计方法在外场进行测试，表1与表2为直I机型的振动测量结果，该机振动信号比较理想；表3与表4为直II机型的振动测量结果，该机振动信号比较恶劣。其中：IPS表示每秒英寸数。测试结果表明，整周期采样时域同步平均短时傅里叶变换提高了振动测量系统的精度、稳定性、可靠性和实时性。

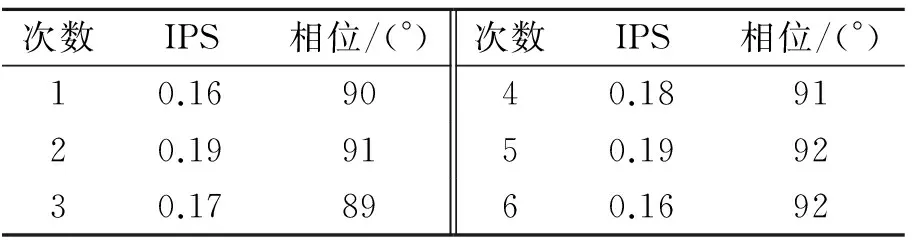
表1 直Ⅰ傅里叶变换

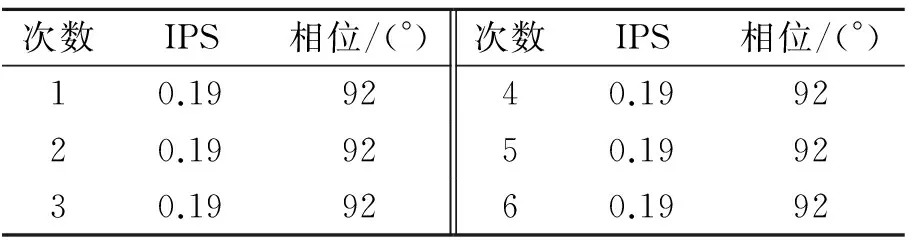
表2 直Ⅰ时域同步平均短时傅里叶变换Tab.2 Synchronous averaging-short Fourier for the helicopter I

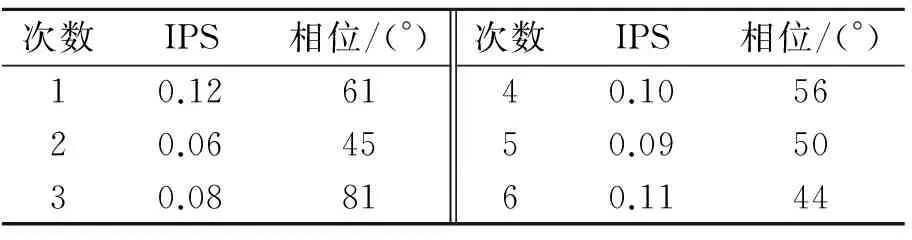
表3 直Ⅱ傅里叶变换

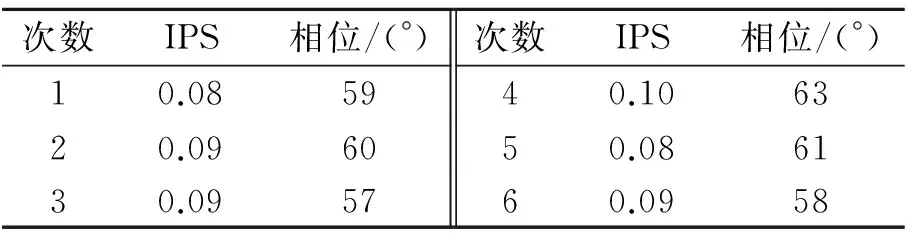
表4 直Ⅱ时域同步平均短时傅里叶变换

4 结论

1) 在对不同型号直升机主旋翼、尾桨振动测量时，该法实时性强，测量时间的长短自适应信号的恶劣程度，解决了采用固定时间傅里叶变换的时间过长问题，提高了嵌入式设备的运行效率。

2) 表1与表2是针对状况良好的直I型机，用不同的方法进行了6次振动幅值与相位的测量比较，验证结果一致。表3与表4是针对状况比较恶劣的直II型机所进行的振动幅值与相位的测量比较，表明整周期采样时域同步平均短时傅里叶变换数据更加集中，尤其在噪声复杂时测量精度、稳定性与可靠性方面都得到了极大的改善，提高了维修效率。

3) 实现了直升机多机型测量的兼容性，解决了测量设备因机型不同须进行软硬件升级等问题。该算法不仅适用于直升机的振动测量，也可用于其他转子振动信号分析。

[1] Randall R B,Antoni J. Rolling element bearing diagnostics-a tutorial[J].Mechanical Systems and Signal Processing,2011,25(2):485-520.

[2] Carden E P，Fanning P. Vibration based condition monitoring: a review[J]. Structural Health Monitoring，2004，3(4)：355-377.

[3] Rubini R，Meneghetti U.Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearings[J]. Mechanical Systems and Signal Processing，2001，15(2)：287-302.

[4] 王大伦，王志新，王康．数字信号处理——理论与实践[M]．北京：清华大学出版社，2010：45-71．

[5] 周晓峰，杨世锡，甘春标．一种旋转机械振动信号的盲源分离消噪方法[J]．振动、测试与诊断，2012，32(5)：714-717.

Zhou Xiaofeng, Yang Shixi， Gan Chunbiao. Denoising vibration signal of frotating machinery[J]. Journal of Vibration ,Measurement & Diagnosis, 2012，32(5): 714-717.(in Chinese).

[6] 杨世锡，梁文军，于保华.振动信号多通道同步整周期数据采集卡的设计[[J]. 振动、测试与诊断，2013，33(1): 23-28.

Yang Shixi, Liang Wenjun,Yu Baohua. Design of vibration signal′s multi-channel integer period synchronous acquistion card[J]. Journal of Vibration ,Measurement & Diagnosis, 2013，33(1): 23-28.(in Chinese)

[7] Rapuano S，Harris F J. An introduction to FFT and time domain windows[J]. Instrumentation & Measurement Magazine，IEEE，2007，10(6)：32-44.

[8] Oliver W，Roland S. Panel contribution analysis-an alternative windows method[J]. Society of Automotive Engineers,2005(1)：2275-2280.

[9] 姜洪开，王仲生，何正嘉.基于自适应提升小波包的故障微弱信号特征早期识别[J].西北工业大学学报，2008，26(1)：99-100.

Jiang Hongkai，Wang Zhongsheng，He Zhengjia. Early identification of weak-signal fault features under very unfavorable environment using adaptive lifting scheme pachet[J]. Joural of Northwestern Polytechnical University, 2008，26(1)：99-100. (in Chinese)

[10]胡劲松，杨世锡，转子振动信号同步整周期重采样的研究[J]．动力工程，2008，28(3)：488-492．

Hu Jinsong，Yang Shixi. Study on method of vibration signal's full period synchronous re-sampling for rotor[J]. Journal of Power Engineering，2008，28(3)：488-492.(in Chinese)