Hilbert-Huang变换中的模态混叠问题*

2016-11-23段玉波刘继承

振动、测试与诊断 2016年3期

关键词：端点极值分量

曹莹，段玉波，刘继承

(东北石油大学电气信息工程学院大庆，163318)

Hilbert-Huang变换中的模态混叠问题*

曹莹，段玉波，刘继承

(东北石油大学电气信息工程学院大庆，163318)

希尔伯特-黄变换(Hilbert-Huang transform，简称HHT)存在的模态混叠现象严重影响了实际应用效果。在分析研究HHT原理及模态混叠产生机理的基础上，提出了基于形态滤波预处理与端点延拓相结合的方法抑制模态混叠现象。与集合经验模态分解(ensemble empirical mode decomposition，简称EEMD)方法比较，所提出的方法能够更快速、准确地分解出表征信号的本征模态函数(intrinsic mode function，简称IMF)分量。将该方法应用于滚动轴承的实测信号分析，结果表明，该方法在实际应用中同样具有很好的模态混叠抑制效果。

经验模态分解；模态混叠；形态滤波；端点延拓

引言

旋转机械振动故障诊断主要是通过对机械设备的振动信号进行一系列处理，进而提取出能够表征机械故障的特征信息，最终实现机械故障的诊断。在工程实际中，旋转机械的振动信号大多为非线性、非平稳的随机信号，而传统的Fourier变换无法满足对此类信号的分析需求。1998年，Huang等人提出了HHT这种新型的时频分析方法，该方法具有分析非平稳、非线性信号及自适应性的特点，在机械故障诊断领域得到了广泛应用[1-3]。

随着HHT的不断推广和应用，也逐渐暴露了在实际应用中的问题。笔者主要针对HHT中的模态混叠问题进行研究，通过对HHT原理及模态混叠现象产生机理的分析，针对性地提出了基于形态滤波预处理与端点延拓相结合的模态混叠抑制方法，并仿真验证其可行性。通过对比分析其与集合经验模态分解方法在抑制模态混叠现象的效果差异，表明所提方法能够更快速、准确地分解出代表信号特征信息的IMF,并在对滚动轴承的实测振动信号分析中同样得到了良好的模态混叠抑制效果。

1 HHT及模态混叠产生机理

1.1 HHT基本原理

HHT主要包括经验模态分解(empirical mode

decomposition，简称EMD)和Hilbert变换(Hilbert transform，简称HT)两部分内容。其中:EMD分解是将原始信号分解成若干个IMF分量;HT是对EMD分解所得的各项IMF分量进行Hilbert变换，得到相应的Hilbert时频谱和边际谱以进行相应的分析[1-2]。

对于任一给定信号，HHT过程如下。

1) EMD分解。首先，确定信号所有的局部极值点；其次，用三次样条插值函数构造上、下包络线，并计算其均值曲线；最后，求取信号与该均值曲线的差，判断其是否满足IMF定义，并根据筛选停止条件反复判断和筛选，直到最后剩余部分为一个单调信号，则分解完毕。

2) HT。EMD分解结束后，对各个IMF分量进行Hilbert变换即可得到解析信号(不含残余趋势项)的Hilbert时频谱及边际谱。

1.2 模态混叠产生机理

模态混叠现象最早是由Huang等通过对含有间断信号的EMD分解时发现的，该现象的产生与EMD分解中求包络均值的筛分过程有关。由于间断信号等一系列不连贯信号的存在导致局部极值点分布异常，为了保证信号包络线的柔性和光滑性，包络将会产生失真而出现模态混叠现象。模态混叠的出现不仅会导致严重错假的时频分布，也使IMF失去了物理意义，严重影响了EMD分解的准确性。后续研究表明，除间断信号外，脉冲干扰和噪声等信号也可引起模态混叠现象[3]。

模态混叠具体有以下两种表现形式：a.单个IMF中包含不同尺度或频率的多个信号；b.同一尺度或频率的信号被分解到多个不同的IMF中。

假设原信号是由频率为50Hz的正弦信号和10dB的白噪声信号叠加而成，则仿真得到图1所示的原始信号(混有噪声的正弦信号时域波形)，图2为对该信号进行EMD分解后得到的IMF分量。

图1 原始信号Fig.1 Original signal

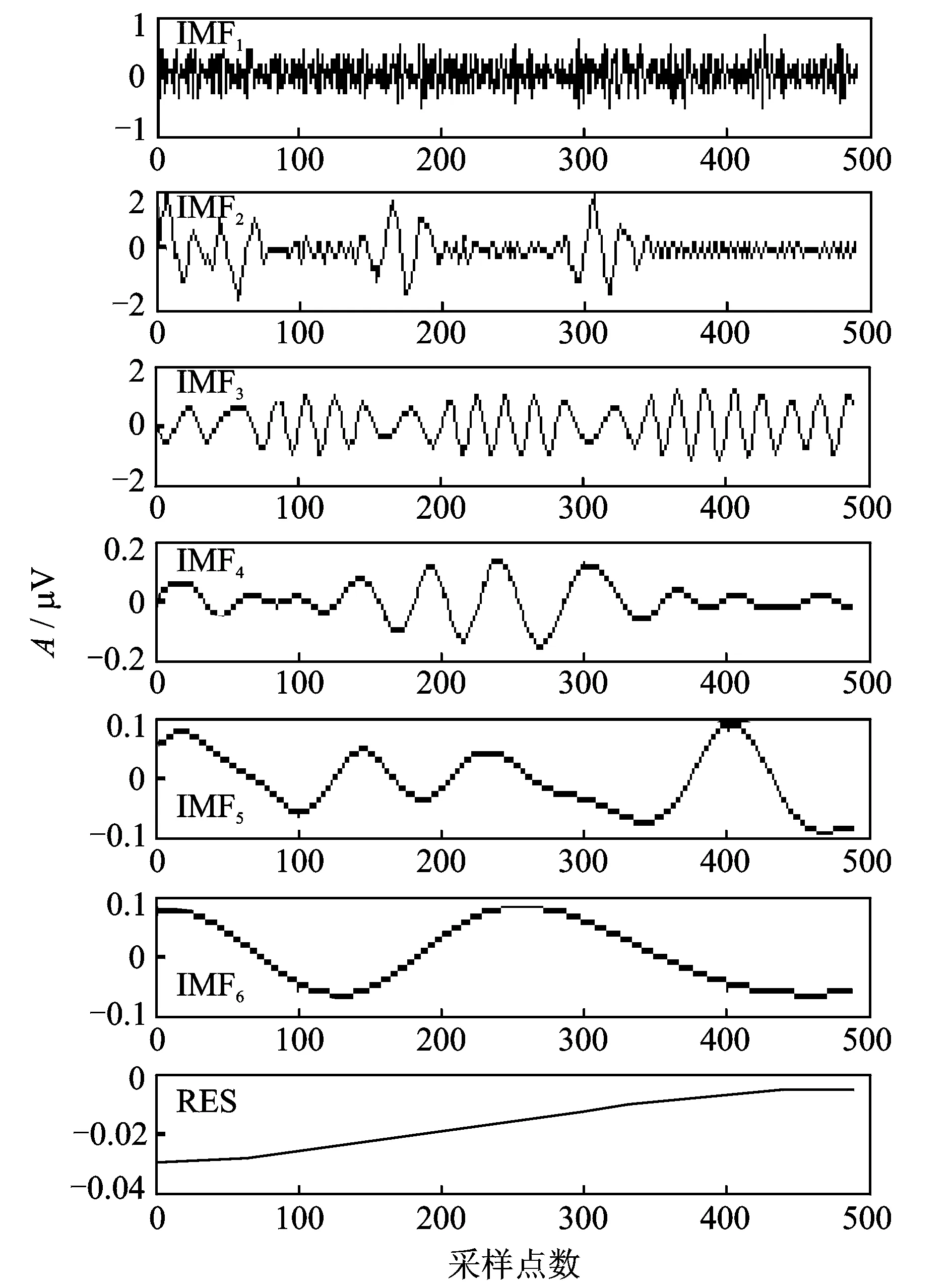
图2 EMD分解后的IMF分量Fig.2 IMF components after EMD

通过对比图2中IMF2,IMF3分量的波形可知，在IMF2中出现了频率较小、幅值较大的IMF3分量中的信号。由此说明，IMF2已经发生了明显的模态混叠现象。

2 模态混叠抑制方法

目前，对于抑制由间断信号和噪声干扰引起的模态混叠现象的方法很多，如中断检测、基于独立分量分析、EEMD以及通过小波变换对信号进行预处理等[4-6]。其中，EEMD主要利用白噪声频谱的均匀分布特性，通过对原始信号多次加入不同的白噪声后进行EMD分解，将多次分解结果进行平均而得到最终的IMF分量，是一种简便易行的分解方法[7-9]。对于旋转机械的振动信号而言，产生模态混叠的主要原因即为环境噪声对极值点的干扰，若采取合理的方法对信号进行降噪处理，将会有效地抑制模态混叠现象。笔者研究了一种组合形态滤波预处理与特征尺度匹配延拓相结合的模态混叠抑制方法，从降噪和波形延拓两方面来改善信号的极值点分布情况，以实现抑制模态混叠的效果。

2.1 形态滤波降噪

与传统的降噪处理方法相比，数学形态学具有计算简单、实用性好及时延较小等优点。它主要包含腐蚀、膨胀、开运算和闭运算共4种基本运算[10-12]。

腐蚀和膨胀是最基本的运算。假设输入序列f(n)为Df=(0,1,…,N-1)上的离散函数，序列结构元素g(n)为Dg=(0,1,…,M-1)上的离散函数，且N≥M，则具体的计算方法如式(1)、式(2)所示

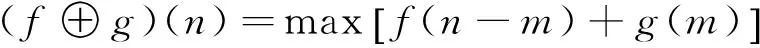
(1)

(2)

其中：m∈0,1,…,M-1。

开运算、闭运算是由膨胀和腐蚀两种运算组合后得到的具有滤波性质的运算方法，具体计算方法如式(3)、式(4)所示

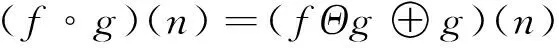
(3)

(4)

基于上述4种运算，笔者通过开、闭运算级联和组合平均构造出一种三角形组合形态滤波器，这是一种平均组合形式的滤波器，能够有效抑制信号中的各种噪声成分。此滤波器输出信号y(n)的表达式为

(5)

开-闭Foc、闭-开Fco的组合运算如下

(6)

2.2 端点延拓

目前，针对数据延拓的方法有很多，如镜像延拓、波形特征匹配延拓、支持向量回归机和神经网络延拓等。在具体应用时，对端点处的数据不能盲目延拓，需要根据信号的特点，选择合适的延拓方法以保证延拓后的波形要符合原始信号在端点处的变化趋势[13-14]。

笔者采用的是一种基于特征尺度匹配的延拓方法，在信号内在规律性较强的情况下，通过采用信号内部和边缘处变化趋势最为相似的子波来对端点处数据进行延拓；在信号内在规律性较弱的情况下，只需考虑边缘处的局部信息，根据边缘局部极值点的特征，在信号边缘两侧各添加一对极大值点和极小值点，对延拓的极值点序列进行包络拟合，估计出均值曲线，即得到完整的延拓波形。下面以信号右边界点数据Sr的延拓为例，说明其具体延拓步骤。

1) 设Mr，Nr为Sr前的第1个极大值点和极小值点，则以Sr-Mr-Nr为边界特征波形，在全部数据中找到与其构成的三角形最接近的波形Sri-Mri-Nri(i=1,2,…)。

2) 计算波形Sri-Mri-Nri与边界特征波形的匹配误差Eri。此时，Eri存在以下两种情况：a.若Eri在误差允许范围内，则取Eri最小的波形为匹配波形，从Sri的后一点数据开始，向后延拓波形数据，使延拓数据符合信号的自然走向；b.若Eri不满足允许范围，即表明信号波形的内在规律不明显，难以找到与端点处变化趋势最为相似的子波，此时，需要根据端点局部极值点的特征进行延拓，即在信号右端添加一对极大值点、极小值点。其中，极值点的幅值根据与端点Sr临近的3(或4)个极大、极小值点的平均幅值确定，对应的添加位置根据与端点Sr最靠近的极大或是极小值点与临近3(或4)个极值点的平均时间间隔确定。添加好极值点后，对新的极值点序列进行包络拟合，进而估计出相应的均值曲线。

该方法在具体实现过程中，仅需一次延拓即可完成，同时能够使延拓后的数据与原始信号特征保持良好的一致性，很好地反映出信号的实际特征。

在HHT过程中，完成对原信号的端点延拓后，需进行正常的EMD分解，对得到的IMF分量做Hilbert变换，然后按原始信号的长度及位置截取有效数据进行相应的结果分析。

2.3 仿真验证

为了验证本方法的可行性，对1.2节中的原信号进行了仿真验证。同时，为了对比说明本方法与传统EEMD的优劣，将两种方法仿真得到的IMF分量进行了对比，具体如图3、图4所示。

图3 EEMD分解后的IMF分量Fig.3 IMF components after EEMD

图4 本方法处理后的IMF分量Fig.4 IMF components after processing

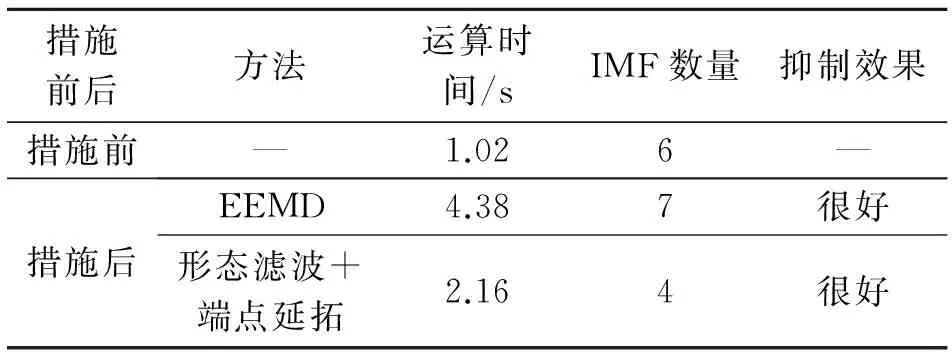
在对比图2～图4的同时，为了进一步分析两种方法在抑制模态混叠方面的优劣，笔者从运算时间、IMF分量个数及抑制效果上进行了差异对比，见表1。

表1 模态混叠抑制效果差异对比

Tab．1 The differences contrast in the effects of mode-mixing restrain

措施前后方法运算时间/sIMF数量抑制效果措施前—1.026—措施后EEMD4.387很好形态滤波+端点延拓2.164很好

通过图2～图4，并结合表1数据的分析可知，经过两种方法处理后，原IMF2分量中的模态混叠现象均得到了很好的抑制。但由于EEMD涉及多次迭代运算，实时性较差，相较而言，本研究方法大大缩减了运算时间，在时效性方面更具优势。此外，根据IMF分量个数的对比可知，EEMD在分解过程中会产生许多无意义的IMF虚假分量，而经本方法处理后的IMF分量个数明显减少，为后续对IMF虚假分量的识别和剔除提供了便利，是较EEMD而言的另一优势所在。

3 实测信号分析

为了进一步验证笔者提出的方法的实操性，在仿真基础上，对型号为HRB-N205EM的滚动轴承进行了实测信号分析。实验原始信号为滚动轴承的振动加速度信号，电机转速为1 450 r/min，采样频率为5 kHz，采样点数为5 000点。

实验测得原始信号的时域波形如图5所示，图6为未采取模态混叠抑制方法所得到的IMF分量，图7为采用笔者提出的模态混叠抑制方法得到的各IMF分量。

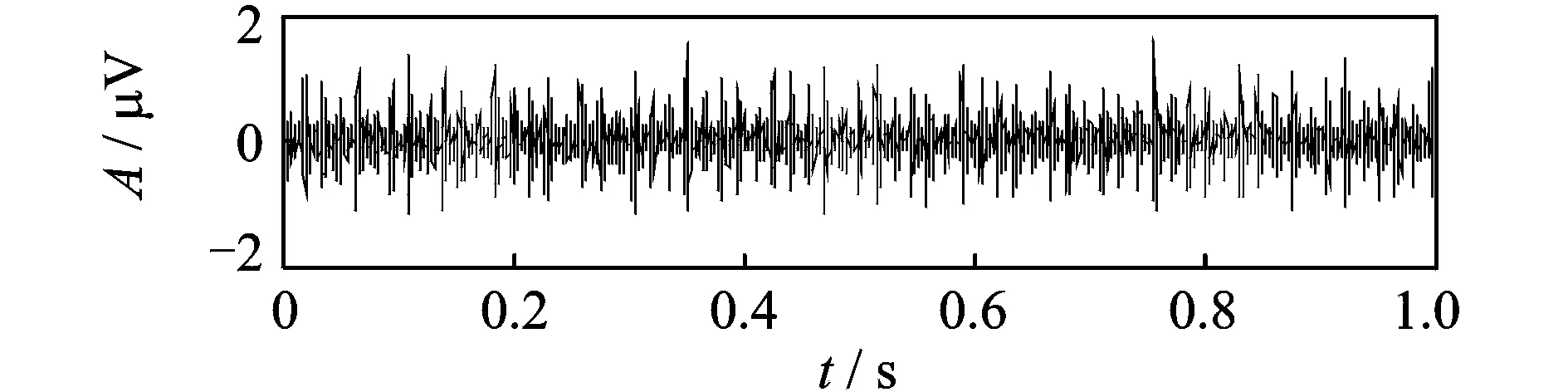
图5 原始实测信号Fig.5 Time domain waveform of the original signal

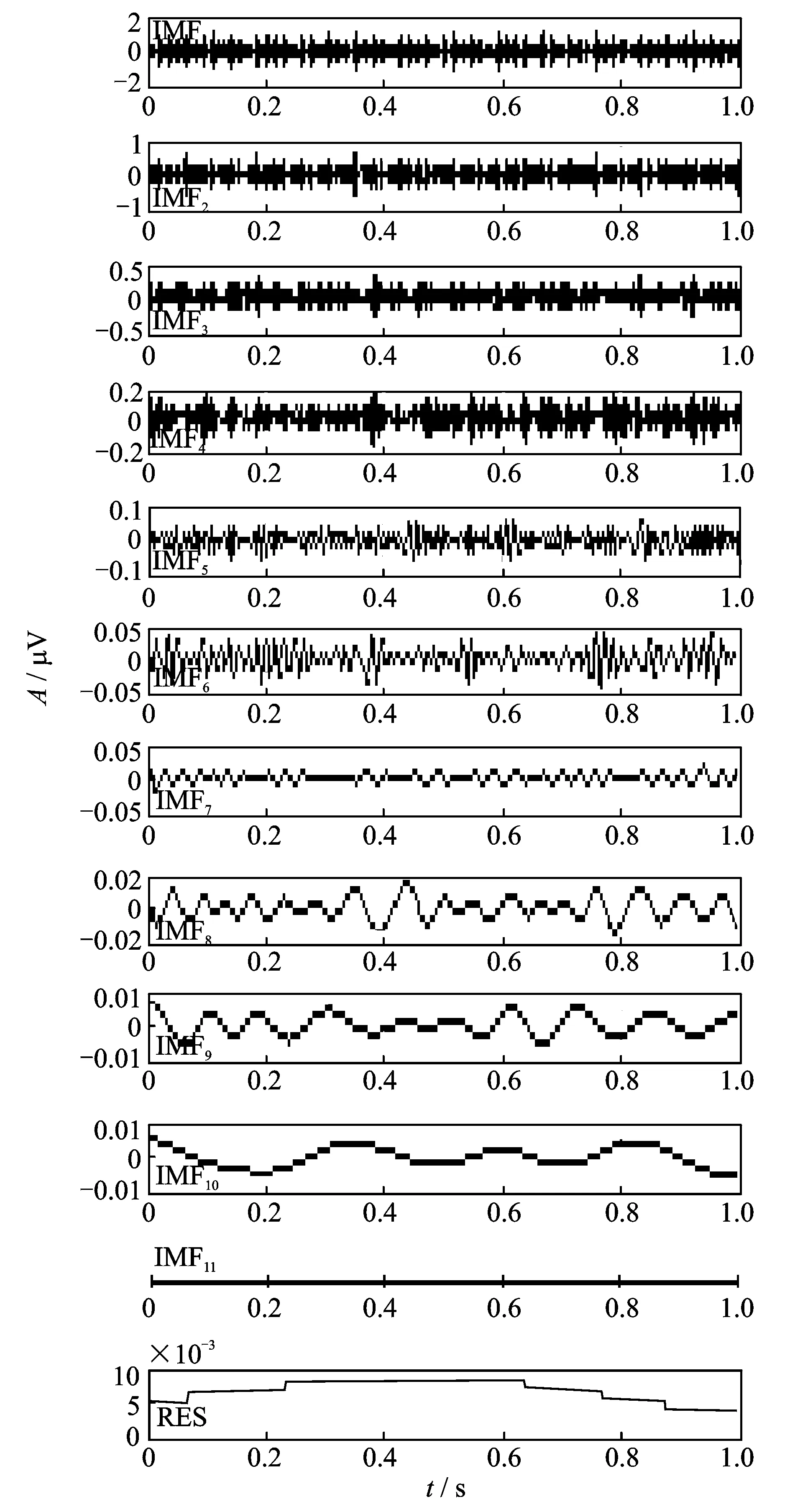
图6 未经处理得到的IMF分量Fig．6 IMF components before processing

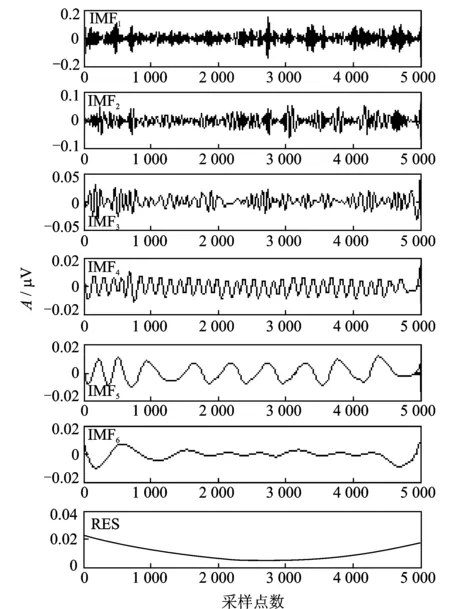
图7 经本方法处理后得到的IMF分量Fig.7 IMF components after processing

根据图6、图7的对比可知，笔者提出的方法在抑制模态混叠现象及减少无意义IMF分量上均有很好的效果。同时，在仿真结果的基础上，综合本次实测信号的分析结果可知，对于滚动轴承故障诊断而言，应优先考虑采用组合形态滤波方法与特征尺度匹配端点延拓方法来抑制模态混叠现象，既可以实现模态混叠现象的抑制，同时为后续的Hilbert变换及相应的故障特征提取打下良好的基础，以实现对故障类型准确、高效的判断。

4 结束语

目前，HHT方法被广泛用于旋转机械故障的分析和诊断。该方法虽然对非平稳、非线性信号的处理具有很大的优势，但仍存在端点效应、模态混叠等问题。笔者通过对HHT原理及模态混叠现象产生机理的分析研究，有针对性地提出了基于形态滤波预处理与端点延拓相结合的模态混叠抑制方法。在仿真验证该方法可行性的同时，从时间、IMF数量等方面对比分析了该方法与传统EEMD的优劣。分析表明所提出的方法能够在抑制模态混叠的同时，更快速、准确地分解出代表信号特征的IMF分量。同时，通过对滚动轴承实测信号的应用分析，进一步验证了该方法在抑制模态混叠实际应用中的良好效果。

笔者给出的方法在进行端点延拓时，需要根据实际情况对匹配误差Eri的限值Lm进行调整。若对信号的规律性要求较低，可将限值设置较大；反之，需要将限值调小。但Lm不可以设置过大，否则延拓后的信号可能会与信号实际趋势相差太远；同样，Lm也不可设置太小，否则会使对信号的规律性要求过于苛刻，导致不能找到合适的匹配波形。

[1] 雷亚国．基于改进Hilbert-Huang变换的机械故障诊断[J]．机械工程学报，2011，47(5)：71-77．

Lei Yaguo．Machinery fault diagnosis based on improved hilbert-huang transform[J]．Journal of Mechanical Engineering，2011，47(5)：71-77． (in Chinese)

[2] 徐晓刚，徐冠雷，王孝通，等．经验模式分解(EMD)及其应用[J]．电子学报，2009，37(3)：581-585．

Xu Xiaogang，Xu Guanlei，Wang Xiaotong，et al．Empirical mode decomposition and its application[J]．Acta Electronica Sinica，2009，37(3)：581-585．(in Chinese)

[3] 胡爱军，孙敬敬，向玲．经验模态分解中的模态混叠问题[J]．振动、测试与诊断，2011，31(4)：429-434．

Hu Aijun，Sun Jingjing，Xiang Ling．Mode mixing in empirical mode decomposition [J]．Journal of Vibration，Measurement & Diagnosis，2011，31(4)：429-434．(in Chinese)

[4] Antonio H C，Stephan H．Adaptive time-frequency analysis based on autoregressive modeling[J]．Signal Processing，2011，91(4)：740-749．

[5] 王晶，陈果，郝腾飞．滚动轴承早期故障的多源多方法融合诊断技术[J]．振动、测试与诊断，2013，33(5)：868-874．

Wang Jing，Chen Guo，Hao Tengfei．Multiple sources and multiple methods about integration of diagnostic techniques based on ball bearing of vibration [J]．Journal of Vibration，Measurement & Diagnosis，2013，33(5)：868-874．(in Chinese)

[6] 汤宝平，董绍江，马靖华．基于独立分量分析的EMD模态混叠消除方法研究[J]．仪器仪表学报，2012，33(7)：1477-1482．

Tang Baoping，Dong Shaojiang，Ma Jinghua．Study on the method for eliminating mode mixing of empirical mode decomposition based on independent component analysis[J]．Chinese Journal of Scientific Instrument，2012，33(7)：1477-1482．(in Chinese)

[7] Zhang Jian，Yan Ruqiang，Gao R X,et al．Performance enhancement of ensemble empirical mode decomposition[J]．Mechanical Systems and Signal Processing，2010，24(7)：2104-2123．

[8] 胡爱军，马万里，唐贵基．基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]．中国电机工程学报，2012，32(11)：106-111．

Hu Aijun，Ma Wanli，Tang Guiji．Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion [J]．Proceeding of the CSEE，2012，32(11)：106-111．(in Chinese)

[9] 陈仁祥，汤宝平，杨黎霞，等．自适应参数优化EEMD机械故障特征提取方法[J]．振动、测试与诊断，2014，34(6)：1065-1071．

Chen Renxiang，Tang Baoping，Yang Lixia，et al．An EEMD-feature extraction method of mechanical fault based on adaptive parameter optimum [J]．Journal of Vibration，Measurement & Diagnosis，2014，34(6)：1065-1071．(in Chinese)

[10]杜必强，唐贵基，石俊杰．旋转机械振动信号形态滤波器的设计与分析[J]．振动与冲击，2009，28(9)：79-81．

Du Biqiang，Tang Guiji，Shi Junjie．Design and analysis of morphological filter for vibration signals of a rotating machinery[J]．Journal of Vibration and Shock，2009，28(9)：79-81．(in Chinese)

[11]宋平岗，周军，陈建亨．形态滤波优化算法用于滚动轴承故障诊断[J]．振动、测试与诊断，2013，33(5)：756-762．

Song Pinggang，Zhou Jun，Chen Jianheng．Fault diagno-

sis method of rolling bearings based on optimized morphological filter algorithm [J]．Journal of Vibration，Measurement & Diagnosis，2013，33(5)：756-762．(in Chinese)

[12]胡振邦，张东升，章云，等．数学形态学滤波器在转子失衡识别中的应用[J]．振动、测试与诊断，2014，34(6)：1038-1044．

Hu Zhenbang，Zhang Dongsheng，Zhang Yun，et al．Research of rotor unbalance recognition based on mathematical morphology filter[J]．Journal of Vibration，Measurement & Diagnosis，2014，34(6)：1038-1044．(in Chinese)

[13]Wu Qin，Sherman D R．Boundary extension and stop criteria for empirical mode decomposition[J]．Advances in Adaptive Data Analysis，2010，2(2)：157-169．

[14]时培明，蒋金水，刘彬，等．基于边界特征尺度匹配延拓的EMD改进方法及应用[J]．中国机械工程，2014，25(12)：1616-1623．

Shi Peiming，Jiang Jinshui，Liu Bin，et al．Improved method of EMD and its applications based on boundary characteristic scale matching extension method [J]．China Mechanical Engineering，2014，25(12)：1616-1623．(in Chinese)