状态热图在AGC伺服缸早期振动辨识中的应用*

2016-11-23陈宏志芦永明王丽娜张云贵于立业

振动、测试与诊断 2016年3期

关键词：热图概率分布值域

刘鸿，陈宏志，芦永明，王丽娜，张云贵，于立业

(中国钢研冶金自动化研究设计院混合流程工业自动化系统及装备技术国家重点实验室北京，100071)

状态热图在AGC伺服缸早期振动辨识中的应用*

刘鸿，陈宏志，芦永明，王丽娜，张云贵，于立业

(中国钢研冶金自动化研究设计院混合流程工业自动化系统及装备技术国家重点实验室北京，100071)

通过对轧制自动厚度控制系统(automated gauge control,简称AGC)伺服缸分别模拟3个阶段的保载和振动加载下所收集到的声发射信号，依托前期研究，探索基于状态热图的AGC伺服缸早期振动的辨识方法。通过在迁安沪久660 mm轧机的AGC伺服缸上模拟保载和早期振动状态，采集声发射信号，对所采集信号的累计概率分布进行分析，选取可表征伺服缸加载状态变化的声发射特征。基于对所选特征进行组合并施加一定的值域约束和逻辑运算条件，构建了AGC伺服缸保载和早期振动的声发射热图。对状态热图的分析结果显示，AGC伺服缸在同等加载状态下的振动和保载状态可较好地通过此类状态热图予以呈现，为AGC伺服缸的早期振动状态提供一种快速、便捷的可视化辨识方案。

AGC伺服缸；声发射；状态热图；振动辨识

1 问题的引出

作为生产高品质钢材工艺过程的最后一道工序，不断增长的工业制造需求对轧制装备的设备性能、可靠性和精度提出了更为苛刻的要求[1]。AGC伺服系统以其响应快速、控制精准、过载保护可靠、维护工作量少以及可在重载和复杂力学环境下实现持续位置控制的特点，在轧机辊缝控制上得到了广泛的应用[2]。伺服液压缸作为AGC系统的执行部件直接与支承辊接触，其性能直接决定了轧制过程的控制精度和产品质量。由于钢铁企业的生产线多为7×24 h不间断连续工作模式，故障和失效时有发生。宝钢的统计数据显示，在轧制类机械装备故障、失效的发生率方面，伺服液压缸达到33.36%[3],如图1所示。然而，对轧机液压系统故障和失效的状态监测与故障诊断方面，现场仍是通过监测整个液压系统的运行状况，再结合经验对系统各部件逐个排查的方式进行，已难以满足目前工业应用的需求。

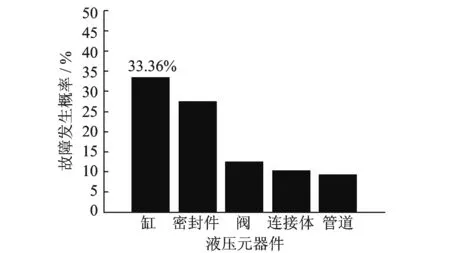
图1 宝钢轧制设备故障发生概率Fig.1 Probability distributions of the faults for the rolling hydraulic components

振动是AGC伺服缸最常见的功能异常之一，导致伺服缸发生振动的原因主要是缸内进入空气或空穴、机械系统异常引起振动、压力和流量脉动大、元件异常或破坏等，这些将引起AGC系统对辊缝控制精度的下降，干扰对轧制产品质量的精确控制[3]。然而，伺服缸是否发生振动需要在伺服缸的振动达到较为显著的状态时才可通过监测AGC系统的输入输出进行判别[4]。基于对谐振噪声更好的鲁棒性以及故障在萌生状态的精准辨识能力，声发射(acoustic emission,简称AE)在复杂机械结构的故障萌生、发展过程的识别以及健康监测中有了较广泛的应用[5-6]。状态热图在笔者前期的研究中，从医学和钢铁冶金领域的应用证实了其可通过较小的计算量为复杂结构的状态辨识提供一种可视化的解决方案[7-8]。本研究的目的是为AGC伺服缸在故障发生前的早期振动提供一种可视化的监测方案，同时考虑以AE为检测媒介，以状态热图为状态表征的方法。利用液压实验平台，对AGC伺服液压缸进行保载和早期振动模拟实验，采集并记录产生的AE信号，通过对信号特征的累计概率分布分析，选取具备统计显著性的6个特征，并基于这6个特征，构建伺服缸在保载和早期振动状态下的AE状态热图模型[9-11]，实现对AGC伺服缸早期振动的可视化监测。

2 AE数据采集实验方案

2.1 测试对象和测试平台

本研究以迁安沪久660 mm轧机的压下厚度控制液压伺服缸为测试对象，活塞直径为550 mm，内径为600 mm，外径为850 mm；缸体材质为碳钢；活塞密封圈材质为聚四氟乙烯；最大工作压力为25 MPa。伺服缸的状态模拟和AE数据采集在45 MN液压伺服缸实验平台上进行，该平台可完成对伺服缸保载、频率响应、启动压力及振动等关键静、动态性能指标的测试和模拟。

2.2 AGC伺服缸数据采集实验方案

数据采集实验的设置如图2所示，数据采集系统由5个压电传感器(型号为PAC-R15i，频率响应为100 kHz～400 kHz，内置固定增益40 dB的前置放大器)、磁性夹具、PAC SH-II型全天候声发射监测系统以及PC机构成。

为保证对测试过程中产生的AE信号进行全方位采集，传感器S2,S3,S4和S5通过磁性夹具固定在缸体表面，与伺服缸活塞等高的位置(离地25 mm)，4个传感器相对于伺服缸横截面圆心呈90°夹角，传感器S1通过磁性夹具固定在距离进油口最近的位置。5个传感器采集到的AE信号通过PAC SH-II全天候声发射监测系统进行信号预处理，SH-II系统通过USB口与PC机相连，完成AE信号的储存和显示。鉴于AGC伺服缸的工作机理，一方面可将其视为重载设备，另一方面可将其视为压力容器。依据ASTM650/650M-12和ASTM E1930/1930M-12标准对压力容器和重载设备的AE检测建议，设定如下AE检测参数：每个AE撞击的总长度为2 ms，采样频率为1 MHz，信号采集门限值为40 dB，峰值定义时间(peak definition time,简称PDT)为200 μs，撞击定义时间(hit definition time,简称HDT)为800 μs。PDT，HDT以及撞击锁定时间(hit lockout time,简称HLT)的具体定义和AE信号的详细采集方案见文献[12]。

工况模拟方面，实验分别采集AGC伺服缸在保载和早期振动状态(发生振动，但未引起失效)下的AE信号。为使实验过程尽可能接近轧制现场工况，且不损坏受测试伺服缸的性能，保载状态下的AE信号通过对伺服缸通入液压油，使伺服缸分别加载至5 MPa(L1)，10 MPa(L2)和15 MPa(L3)，并分别保持300 s的方式采集。为保证在实验过程中不影响受测试样品的性能，伺服缸早期振动状态的AE信号通过对伺服缸分别加载至5 MPa(V1)，10 MPa(V2)和15 MPa(V3)，并对活塞施加20 Hz振荡信号，分别保持300 s的方式进行模拟和采集。

图2 数据采集实验示意图Fig.2 Demonstration of AE data acquisition experiment from the cylinder under examination

3 声发射信号的定量分析

完成信号采集实验后，首先对6种状态下产生的AE信号数量进行分析。笔者选取了从传感器S3中获取的AE信号进行定量分析，在前期进行的研究中已证实从传感器通道S3中所获得的AE信号可较好地反映油缸的加载变化情况[8]。

在本研究中的6种状态下，伺服缸产生的AE信号数量的柱图如3所示，图中横坐标为受测试对象的加载状态，纵坐标为每秒产生的AE撞击数的平均值。保载方面，当伺服缸处于状态L1时，产生的AE信号数量在所有测试状态中最少，每秒AE信号数量随着加载压力的增大而增大。保载状态的AE信号数量的最大值出现在15 MPa时，此状态下产生的平均AE信号撞击数每秒达到10.4个。

早期振动状态下产生的AE信号在数量上同样呈现随压力增长而增加的趋势。与保载状态不同的是，当伺服缸加载至V1状态时，产生了约5倍于L1的AE撞击数。随着加载的不断增大，AE信号数量相对于5 MPa时有一定的增加，且高于同等压力下伺服缸处于保载状态时所产生的AE信号。保载和早期振动状态下的AE信号数量的最大值出现在V3状态，在此状态下，300s振动产生的平均AE撞击数每秒达到12.24个，略高于伺服缸在L3状态下每秒产生的AE撞击数。

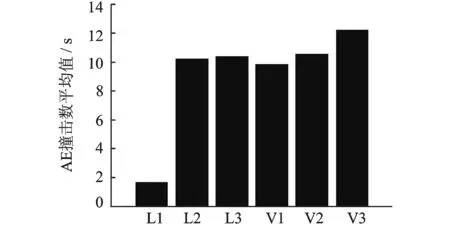
图3 伺服缸在6种工况下每秒产生的平均AE信号数量Fig.3 Average number of hits per second for the cylinder under 6 experimental conditions

4 AE信号的统计分析与特征选取

通过对每一个AE撞击提取时、频域特征，并进行累计概率分布分析[13]。根据概率分布曲线重叠度尽可能小，并且特征值域随加载状态的变化体现差异化分布的这个规则，笔者选取了峰值(每个AE撞击的峰幅值(peak amplitude,简称Amp)、脉冲计数(每个AE撞击越过门槛值的脉冲数，简称Counts)、峰值计数(信号脉冲从第1次越过门槛值到峰值出现之间，越过检测门槛的信号脉冲数(counts to peak ，简称CTP))、持续时间(每个AE撞击第1次越过门槛值和最后1次越过门槛值的时间间隔，简称Dur)、上升时间(信号脉冲首次越过门槛值到峰值出现的时间(rise-time,简称RIST))和平均幅值(每个AE撞击在信号持续时间内的信号平均幅值(average signal level over duration,简称ASLOD))6个具有统计显著性的AE特征，用于进一步实现对伺服缸的状态监测。

6个信号特征的累计概率分布如图4所示，从图中可以看出，伺服缸在同等加载情况下，超过95%的信号的Amp值域分布出现重叠，但是在累计概率分布图的尾部，可以观察到约1%的信号特征分布曲线出现分离的情况。CTP的累计概率分布在所选6个特征中呈现最大程度的显著性，虽然约90%的信号特征遵循相似的分布轨迹，但是无论在保载还是早期振动状态下，各状态CTP分布曲线的最大值呈现随压力增大而增大的现象。由RIST的分布曲线可见，有超过50%的累计概率分布曲线出现不重合。伺服缸6种加载状态所产生AE信号的Dur分布曲线的两个端点值具有很高的相似度，都在0～2 000 μs之间变化，但6种状态的累计概率分布曲线在0～1 500 μs这个值域范围内出现了一定程度的分离。在ASLOD的分布图中可观测到相似的现象，约75%的ASLOD值分布在20～40 dB之间，且分布曲线呈现出分离的现象。AE信号脉冲数的累计概率分布随着加载的增大，最大值呈现增大的趋势。此外，从各状态下所采集的AE信号的累计概率分布曲线看，约有25%的曲线呈现出不重合的分布。

综上，伺服缸在各状态下产生的AE信号在特征分布上呈现相似度高、但小部分特征分布随着伺服缸加载状态的变化而出现差异的特点，这与受测试对象的实际状态匹配，即伺服缸虽然出现了早期振动的现象，但振动仍处于容错范围内。

5 AGC伺服缸的声发射热图

依据上面的分析，虽然所选取的6个信号特征的累计概率分布在一定程度上呈现出差异化分布，但所选取特征的累计概率分布仍呈现了很高的相似度，直接使用单一特征仍然难以实现对所测试6个状态的辨识和监测，直接分析所获取的全部特征或全波形，也会产生较大的计算开销[9]。为此，笔者引入了状态热图模型[9-11]，最早在生物医学工程领域应用于基于声发射的人体膝关节老化趋势的可视化。冶金工业领域的应用中，状态热图模型也已证明可用于表征AE信号与AGC伺服缸加载变化间的关联[8]。状态热图的基本构建思路是通过对受测试对象在受加载状态下产生的AE信号，选取具备关联性的特征，并加入一定的逻辑运算条件，以满足条件的AE信号数量来表征热图中每个像素的亮度，在二维空间内构建可视化热图。状态热图的数学表达式如下

(1)

其中：N为根据特征值域约束返回的AE信号数量；V1,V2,…，Vi分别为所选取的伺服缸AE特征；Fψj为所选特征值域约束的集合。

从累计概率分布分析的结果可见，伺服缸AE信号随着加载压力和工作状态的变化，Amp，Counts，

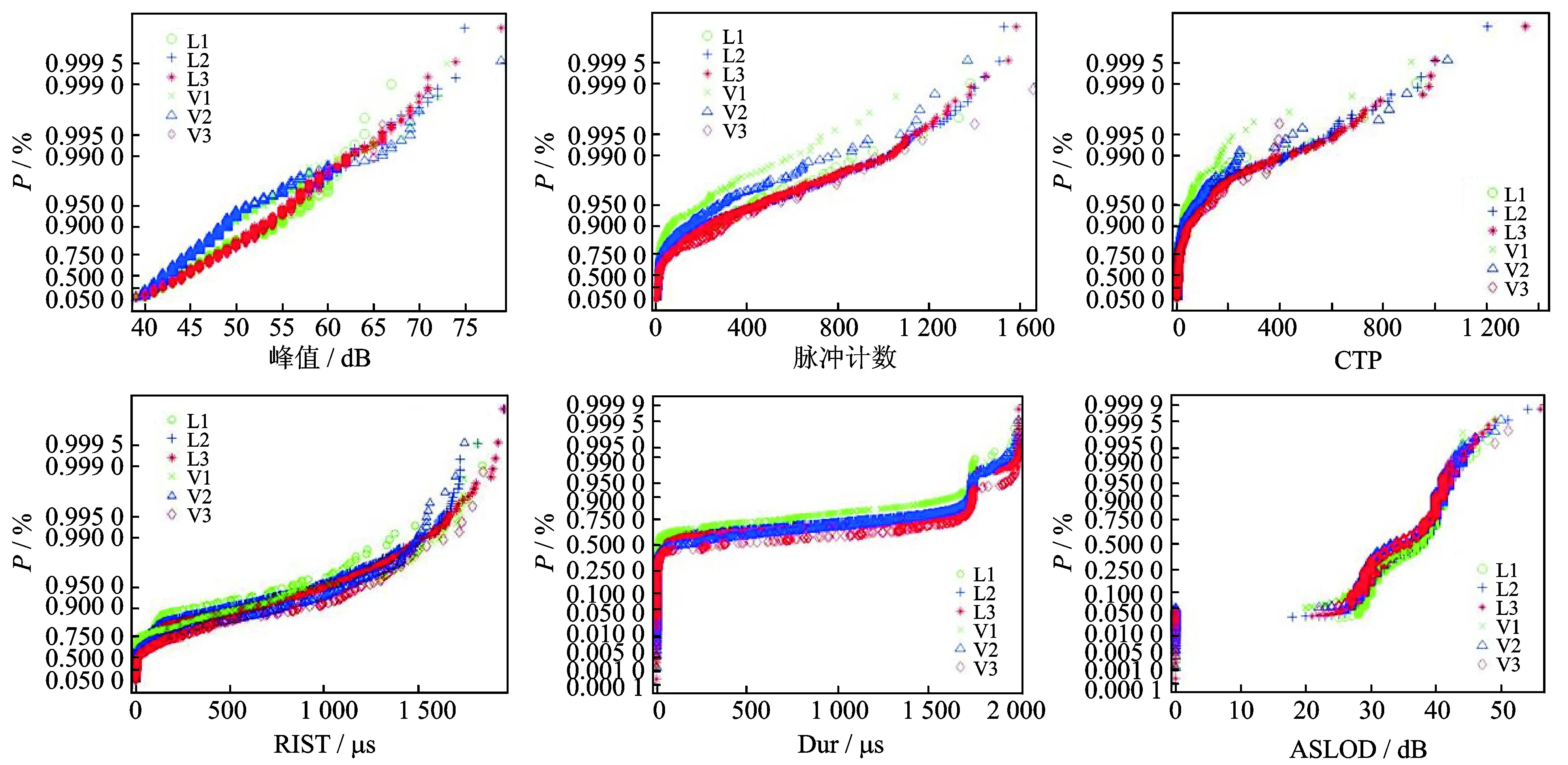
图4 信号特征的累计概率分布Fig.4 Cumulative probability distribution of the selected features

CTP，Dur，RIST，ASLOD 6个特征呈现一定的差异化分布。为此，笔者通过对这6个特征增加值域限定条件的方式构建状态热图。鉴于一个二维平面内最多可容纳4类的特征组合，且从数据可视的角度，每一类组合最多可包含两种特征维度，为此，在每个子热图中，图像的每个像素按照式(2)所示的规则进行定义

(2)

其中：Fψj(V1)和Fψj(V2)表示在ψj象限(子热图区间)中所包括的特征。

各个子热图中，每个图像的像素值(特定值域约束下返回的AE撞击数)可通过式(3)进行定义

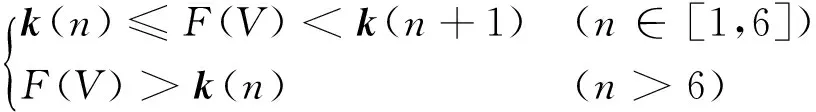
(3)

其中：k(n)为包含AE特征值域的向量。

为了能更清晰地通过可视化的方式展示AGC伺服缸AE信号与其状态变化间的关系，与文献[5, 9-11]的研究成果类似，将所选特征的4种不同组合方式考虑成在一个二维平面内，分布在4个象限内的4幅子热图的拼接，如图5所示。图像中每个像素点的像素值(撞击热度)表示满足两个特定特征值域约束的AE信号撞击数，各特征的值域以原点为中心，向四象限的方向增加。

图5 AE热图构成示意图Fig.5 Configuration of the AE hits density model

6 基于状态热图的伺服缸状态辨识

图6为本研究中所测试6种状态下的AGC伺服缸的AE信号热图，6个AE信号特征在图中的分布如5 MPa保载的热图所示。所选的6个特征的值域分别定义如下：峰值kAmp=[40 50 60 70 75 80 85]T；峰值计数kCTP=[1 250 500 750 1 000 1 250 1 500]T；上升沿时间kRIST=[0 300 600 900 1 200 1 500 1 800]T；持续时间kDur=[0 300 600 900 1 200 1 500 1 800]T；平均幅值kASLOD=[0 10 20 30 40 50 60]T；脉冲计数kCounts=[1 250 500 750 1 000 1 250 1 500]T。

图6中伺服缸的3个保载状态(L1～L3)和早期振动状态(V1～V3)的AE热图分别排列在图的左右两列，状态热图的显著差异如图中的标记所示。从总体上分析，保载和振动状态下所产生的AE热图从图像热度以及非零像素的类型上，都具有较高的相似度(即AE信号类型和数量都具有较高的相似度)，这与被测试伺服缸的实际状态相符，即该伺服缸虽然由于加载及工作状况的变化产生了AE信号，但是伺服缸并未发生故障。结合现场工况，伺服缸的工作原理是向其通入液压油，并加载至指定的保载状态，以保证可提供持续的辊缝控制[1]，而伺服缸的振动将直接影响到辊缝的控制精度。作为AE状态热图在AGC伺服缸早期振动监测上的探索性研究，笔者首先考虑基于状态热图实现同加载状态下保载和振动的可视化辨识。

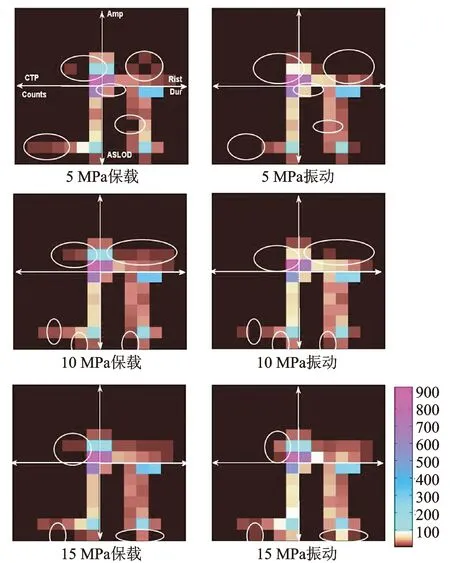
图6 保载和早期振动状态下的伺服缸状态热图模型Fig.6 Hits density images of the cylinder under 6 loading conditions

比较伺服缸在 5 MPa状态下的保载和振动的状态热图可见，伺服缸只在未发生振动时，产生了峰值在50～60 dB，CTP值在500～750范围内的AE信号。分析热图的第二象限可见，状态L1产生了峰值为50～60 dB，Rist值在600～900、峰值在50～60 dB，Rist值在1 200～1 500以及峰值在70～80 dB，Rist值在900～1 200的AE信号。

比较伺服缸在10 MPa状态下的AE热图，在热图的上半部分，总体上L2产生信号的数量要显著多于V2。在由Amp和Rist构成的子区域内可见，伺服缸在L2状态下产生了峰值在50～60 dB，CTP分别在250～500以及500～750的AE信号。更为显著的差异出现在由Amp和Rist构成的状态热图子区间，在50～60 dB的峰值带可见，L2状态所产生的AE信号沿着Rist的增长方向增加。此外，部分的细微差异可在热图的下半部分观测到，在由Counts和ASLOD构成的热图子区间里，Counts值在750～1 000且ASLOD值在50～60 dB的AE信号，以及Counts值在250～500，ASLOD值大于60 dB的AE信号只在L2状态下产生；而Dur值在600～900 μs且ASLOD大于60dB的AE信号只在V2状态下产生。

类似的，比较伺服缸状态L3及V3，如图6中最底部两幅热图及图中的标记所示，在图像的第一、三、四象限可见细微的不同，L3状态下产生Amp在50～60 dB，CTP在750～1 000的AE信号，而此类信号并未在V3状态下出现；具有最大ASLOD值且Counts值在750～1 000的AE信号仅在V3状态下出现；具备ASLOD最大值且600～900 μs和1 200～1 500 μs的AE信号仅出现在V3状态。

综上，分析伺服缸在同等加载状态下产生的AE状态热图可见，信号峰值在50～60 dB，且峰值计数在250～750的AE信号，以及峰值在50～60 dB，且上升沿时间在600～1 500 μs的AE信号可作为辨识伺服缸在5 MPa和10 MPa加载状态下的早期振动。ASLOD值在40～60 dB，且Counts值和Dur值分别在750～1 000和600～1 500 μs的AE信号可作为辨识伺服缸在10 MPa和15 MPa加载状态下的早期振动。

7 结论

1) 讨论了AE状态热图模型在AGC伺服液压缸早期振动辨识中的探索性应用，为AGC伺服缸的早期振动监测提供了一种可视化的方案。通过对伺服缸在5 MPa～15 MPa加载下，常规的保载以及伺服缸的早期振动状态下获取的AE信号进行累计概率分布分析可见，虽然峰值、脉冲计数、峰值计数、平均幅值、持续时间和上升沿时间在累计概率分布上呈现分布相似度高，但是特征的累计概率分布在局部呈现出了统计显著性。这与受测试伺服缸的实际状态相符，即伺服缸虽然出现了早期振动的现象，但振动仍处于容错范围内。

2) 通过分析与伺服缸状态变化具有一定显著性相关的6个特征(Amp，CTP，Counts，Dur，Rist，ASLOD)构建的伺服缸保载和早期振动的状态热图可见，在同等加载状态下，保载和早期振动状态的热图虽然呈现很高的相似度，但在热图的某些特定区域内仍可观测到差异。特别是在50～60 dB峰值带，具备不同Rist值的AE信号，以及在高平均幅值带，具备不同Counts和Dur值的AE信号。状态热图上显示出的这些细微的差异证实了依托AE信号，使用此类模型可视化辨识AGC伺服缸早期振动的可能性。

[1] Gajdzik B, Sitko J. An analysis of the causes of complaints about steel sheets in metallurgical product quality management systems [J]. Metalurgija, 2013, 53(1): 135-138.

[2] Liu Hong. Application of predicted extrapolation control strategy in hot strip rolling mills gauge system [C]∥World Automation Congress (WAC). Mexico: IEEE, 2012:1-4.

[3] 叶维明，徐致让，邓克. 冶金设备液压系统的故障及诊断 [J]. 中国高新技术企业，2008，24：124-129.

Ye Weiming, Xu Zhirang, Deng Ke. The fault and diagnosis for hydraulic system of metallurgical machinery[J]. China High Technology Enterprises, 2008, 24: 124-129. (in Chinese)

[4] 邓克，席素奕. 冶金设备液压系统的常见故障及诊断技术[J]. 机械工程师，2006，8：123-124.

Deng Ke, Xi Suyi. Diagnosis techniques for common faults of metallurgical hydraulic systems [J]. Mechanical Engineer, 2006,8: 123-124. (in Chinese)

[5] Chen Hongzhi. Discovery of acoustic emission based biomarker for quantitative assessment of knee joint ageing and degeneration[D]. Preston: University of Central Lancashire, 2011.

[6] 操礼林，李爱群，邓扬,等. 声发射和小波包分析在损伤状态监测中的应用 [J]. 振动、测试与诊断，2012，32(4)：591-595.

Cao Lilin, Li Aiqun, Deng Yang, et al. Degeration monitoring based on acounstic emission and wavelet packets[J]. Journal of Vibration, Measurement and Diagnosis, 2012, 32(4): 591-595. (in Chinese)

[7] 陈宏志，芦永明，王丽娜,等.较小样本动态声发射信号多元统计分析技术[J]. 振动、测试与诊断，2013，33(2)：199-203.

Chen Hongzhi, Lu Yongming, Wang Lina, et al. Analysis of dynamic acoustic emission signals using multivariate statistical technique for smaller dataset [J]. Journal of Vibration, Measurement and Diagnosis, 2013, 33(2): 199-203. (in Chinese)

[8] Chen Hongzhi, Wu Chao, Sun Yanguang, et al. State identification of automatic gauge control hydraulic cylinder using acoustic emission[C]∥Proceedings of 2013 Chinese Intelligent Automation Conference. Yangzhou: Springer, 2013: 585-594.

[9] Shark L K, Chen Hongzhi, Goodacre J. Knee acoustic emission: a potential biomarker for quantitative assessment of joint ageing and degeneration[J]. Medical Engineering & Physics,2011, 33(5): 534-545.

[10]Shark L K, Chen Hongzhi, Goodacre J. Discovering differences in acoustic emission between healthy and osteoarthritic knees using a four-phase model of sit-stand-sit movements[J]. The Open Medical Informatics Journal,2010, 4: 116-125.

[11]Mascaro B, Prior J, Shark L W, et al. Exploratory study of a non-invasive method based on acoustic emission for assessing the dynamic integrity of knee joints[J]. Medical Engineering & Physics,2009, 31(8): 1013-1022.

[12]Physical Acoustics Corporation. PCI-2 based AE system user′s manual[R]. NJ:Physical Acoustic Corporation, 2007.

[13]Jessica U.Seeing through statistics[R]. United States of America: Thomson Brooks/Cooe, 2005.