车削加工颤振稳定性可靠度蒙特卡罗法仿真*

黄贤振, 许乙川, 张义民, 谭学飞

(东北大学机械工程与自动化学院 沈阳,110819)



车削加工颤振稳定性可靠度蒙特卡罗法仿真*

黄贤振, 许乙川, 张义民, 谭学飞

(东北大学机械工程与自动化学院 沈阳,110819)

在工程实际中，车削系统刚度、阻尼及切削力等参数的随机性严重影响车削加工的稳定性。针对此问题，提出了一种车削加工再生型颤振稳定性可靠度计算方法。考虑随机因素的影响，采用蒙特卡罗数值模拟方法，研究车削加工再生型颤振稳定性的统计分布规律。建立车削加工再生型颤振动力学模型, 采用拉氏变换获取机床车削的极限切削宽度及所对应的主轴转速。根据数控车床切削系统动力学参数的分布信息抽取样本，代入再生型颤振模型进行计算，获取极限切削宽度的样本，并统计其概率特性，以实际切宽是否小于极限切宽为判别条件提出一种基于蒙特卡罗模拟的车削加工再生型颤振稳定性可靠度预测方法。

再生型颤振； 数控车床； 可靠性； 稳定性

引 言

在数控切削加工过程中，切削振动严重影响工件的加工质量和生产效率。研究表明，切削振动往往是由系统内部的“再生反馈”所引起的，这类振动被称为自激振动(即颤振)[1]。根据反馈量和反馈方式的不同，切削颤振大体可以分为再生型切削颤振、振型耦合型切削颤振和负摩擦型切削颤振。其中，再生型切削颤振是金属切削加工过程中最主要的颤振形式，也是对加工影响最显著的因素[2]。文献[3]建立了切削颤振动力学分析模型, 研究了切削颤振的相位特性。文献[4]着重研究了轴向切削力与陀螺效应对颤振稳定性的影响，并开展了动态切削实验验证了理论模型的正确性。文献[5]分别在频域和时域范围内提出了铣削加工颤振稳定性分析模型，并通过实验验证了所提出模型的正确性。文献[6]研究了一种应用连续小波特征和多类球支持向量机进行铣削系统颤振预报的方法。文献[7]通过对阻尼器的刚度、阻尼参数进行优化抑制车削颤振。文献[8]研究了数控机床子系统振动耦合对加工稳定性的影响。文献[9]建立了重型铣削机床的稳定性分析模型，并以此模型为基础开展了工艺规划与刀具选择过程优化研究。

上述研究中，通常将切削参数信息视为确定、无误差的，而在实际工程问题中，确定性因素极少，大部分都是随机因素。这些不确定因素是工程实际中所固有的，对金属切削过程有着不可忽视的影响。传统切削颤振稳定性分析模型忽略了不确定因素的影响，势必会造成一定的分析误差。因此，按照确定性方法制定出来的切削加工方案，在工程应用中很可能会出现性能偏差，往往难以实现预期的效果。笔者综合考虑随机因素对金属切削颤振的影响，采用蒙特卡罗数值模拟方法，提出一种金属切削过程中颤振稳定性可靠度计算方法。

1 车削加工再生型颤振稳定性分析

车削加工再生型颤振是由于前一次车削加工所形成的振纹与后一次车削振动位移之间的相位差导致刀具切削厚度的不同而引起的颤振[10]。常用再生型车削颤振系统动力学模型如图1所示。

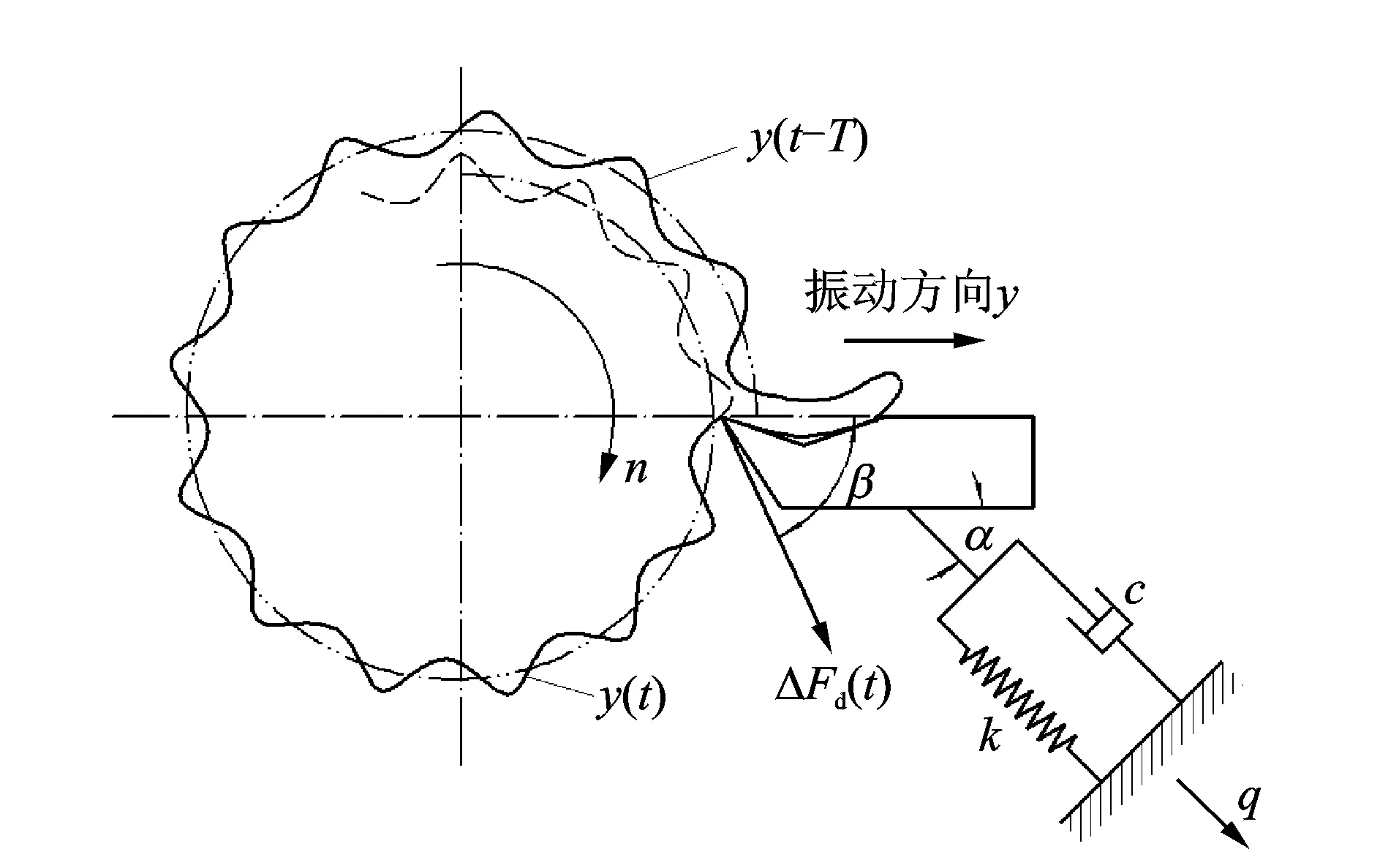
图1 再生型车削颤振系统动力学模型Fig.1 Dynamic model of regenerative turning chatter system

根据图1所示动力学分析模型，再生型车削颤振微分方程[1-3]为

(1)

其中：m为车床振动系统的等效质量；c为等效阻尼；k为等效刚度；β为动态切削力ΔFd(t)与刀具振动方向的夹角；α为主振方向q(t)与刀具振动方向的夹角。

由切削厚度变化引起的动态切削力ΔFd(t)为

(2)

其中：b为切削宽度；kc为单位切削宽度上的切削刚度系数；y(t)=q(t)cosα为刀具振动位移；0<μ<1为前后两(转)次切削的重叠系数。

将式(2)代入到式(1)中，进一步整理可得再生型车削颤振微分方程为

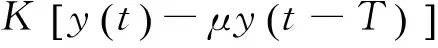
(3)

设车削振动的动态响应为

(4)

将式(4)代入式(3)中，经过整理可得

(5)

对式(5)进行拉氏变换得车削颤振系统的特征方程

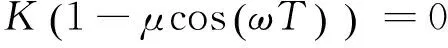
(6)

车削振动系统的稳定性状况取决于特征方程根s=σ+iω的性质，若s的实部σ>0，系统处于失稳状态；若σ<0，系统处于稳定状态；若σ=0，系统处于临界状态。令σ=0，将s= iω代入式(6)得

（二）合理、动听、巧妙、生动的教学专业用语是渗透情感教育的成功所在。教师在教学中，应该在熟悉教材的教材行，认真备课，才用生动、形象的语言为学生打开情感的大门，教师首先要能够进入角色，扮演在教学中具有正能量的教育工作者的光辉形象，让学生在不知不觉的学习思想品德知识的同时，进入情感教育的状态，并以此在完成学业。用能够激发学生情感的语言，把课本中无声的文字体现在有声有情的语言，以此来影响学生。

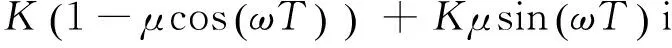
(7)

要想式(7)成立，等式左右两边的实部与实部应分别相等，则有

(8)

令λ=ω/ωn，式(8)可以进一步转换为

(9)

通过求解式(9)，可得机床车削的极限切削宽度为

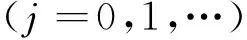
(10)

所对应的主轴转速为

(11)

将机床车削系统相关动力学参数k,ζ,ωn,μ,u,kc代入式(10)和式(11)，即可求得j=0,1,…时所对应的主轴转速n值和极限切削宽度blim值。

切削重叠系数越大，越容易产生颤振。将μ=1代人式(9)，经过整理可得极限切削宽度最小值的计算公式

(12)

2 颤振稳定性可靠度计算

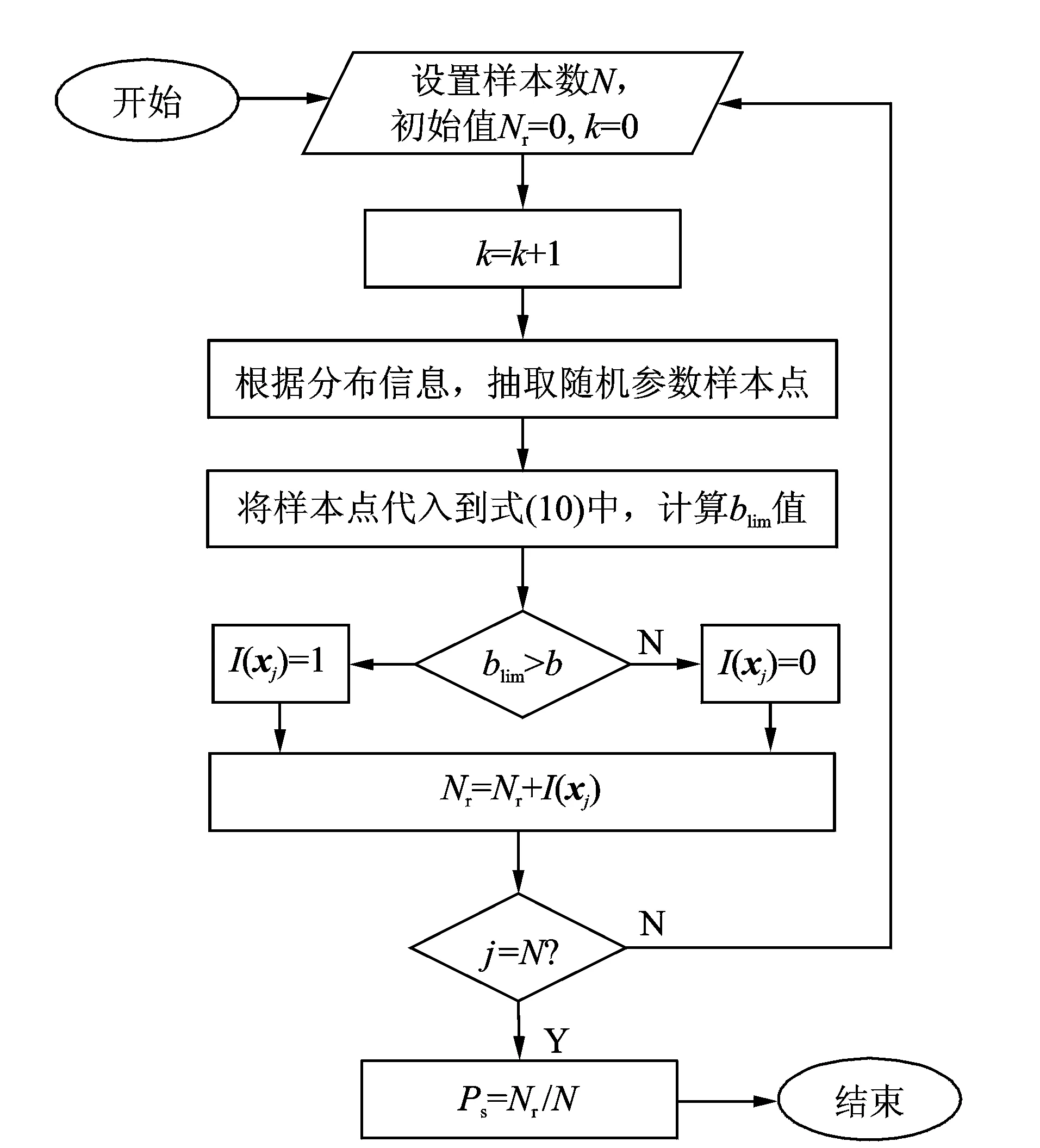
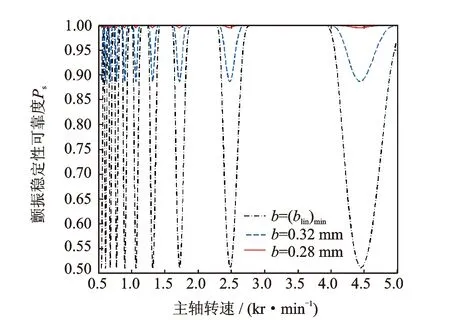
机械可靠性是指机械产品在规定时间内规定条件下完成规定功能的能力,采用概率的方式度量这种能力即为可靠度。目前，机械可靠性分析方法主要有矩方法和蒙特卡罗模拟法两类。与矩方法相比，蒙特卡罗模拟法具有通用性强、计算精度高等优点。但是蒙特卡罗方法以大量模拟计算为基础，不适合复杂数值模型(如有限元)的可靠度。由于数控极限切削宽度为显式表达式，故笔者采用蒙特卡罗模拟方法进行颤振稳定可靠度计算。数控车床颤振稳定性可靠度为实际切削宽度小于极限切宽(即b

Ps=∫…∫b < blim (x)fX(x1,x2,…,xn)dx1dx2…dxn

(13)

其中：x1,x2, …,xn为随机设计变量(如动力学参数k,ζ,ωn,μ,u,kc等)；n为随机设计变量的个数；fX(x1,x2, …,xn) 为随机设计变量联合概率密度函数。

若随机设计变量相互独立，则有

(14)

其中:fXi(xi)(i=1, 2, …,n)为随机变量xi的概率密度函数。

蒙特卡罗法求解切削颤振稳定性可靠度的基本思路为：由基本随机变量的联合概率密度函数fX(x)产生N组随机样本xj(j=1, 2, …,N)，将N个随机样本代入机床车削的极限切削宽度函数表达式，统计大于实际切削宽度b的样本点数Nr，用频率Nr/N近似代替可靠度Ps，即

(15)

其计算流程如图2所示，具体步骤如下：

1) 确定蒙特卡罗模拟的次数N；

2) 根据设计参数的分布信息，抽取N组样本；

3) 将样本代人车削加工再生型颤振稳定性分析模型，计算极限切削宽度blim；

4) 计算切削稳定性可靠度。

图2 颤振稳定性可靠度计算流程图Fig.2 Flow chart for calculating chatter stability reliability

3 数值算例

某数控车床颤振系统的等效刚度k=3 100 N/mm，等效阻尼c=0.6(N·s)/mm，等效质量m= 0.01 (N·s2)/mm，主振方向与刀具振动方向的夹角α=60°，动态切削力与刀具振动方向的夹角β=45°，单位切削宽度上的切削刚度系数kc=2 018 N/mm2，前后两转(次)切削的重叠系数μ=1。估算数控车床车削的颤振稳定性可靠度。

具体步骤如下：将数控车床切削系统动力学参数k,c,m,α,β,kc和μ分别代入式(10)、式(11)和式(12)，可得数控车床颤振稳定性瓣图(图3)以及极限切削宽度最小值(blim)min=0.36 mm。

图3 数控车床切削稳定性叶瓣图Fig.3 Stable lobe graph of CNC lathing

随机参数的方差的取值应通过测试或者实验数据的统计分析获得，有关金属材料的机械性能参数的标准差，可以根据变差系数c来确定，一般取c=0.05[11]。随机变量如果受到大量的独立因素的影响(无主导因素)，则一般服从正态分布[11-12]。

图4 数控车床切削颤振稳定性可靠度Fig.4 Chatter stability reliability of CNC lathing

按照图2所示步骤，采用105次蒙特卡罗抽样模拟数控车床切削过程，获取极限切削宽度blim的样本。图4为实际切削宽度分别为b=(blim)min,b=0.32 mm,b=0.28mm三种情况下，数控车床切削颤振稳定性可靠度。计算结果表明：切削宽度b=(blim)min时，颤振稳定性状况较差，发生失稳的可能性较大，可靠度的最小值为0.512；切削宽度b=0.32 mm时，颤振稳定性得到了显著的改善，发生失稳的可能性不大，可靠度的最小值为0.886；切削宽度b=0.28 mm时，颤振稳定性状况很好，发生失稳的可能性很小，可靠度的最小值为0.995。

4 结束语

笔者基于蒙特卡罗模拟，提出了一种车削加工再生型颤振稳定性可靠度计算方法。与传统切削力预测方法相比较，所述方法考虑数控车床颤振系统的刚度、阻尼、质量以及单位切削宽度上的切削刚度系数等随机参数对切削稳定性的影响，更加符合工程实际状况。采用所述方法可以迅速获取金属车削过程中不同主轴转速时切削稳定性的可靠度，对提高工件的加工精度，保证刀具的使用寿命，提高生产效率等具有参考价值。

[1] 于骏一，吴博达. 机械加工振动的诊断、识别与控制[M]. 北京：清华大学出版社, 1994:9-50.

[2] 刘强，李忠群. 数控铣削加工过程仿真与优化:建模、算法与工程应用[M]. 北京：航空工业出版社，2010:57-93.

[3] 付连字, 于骏一，鲍明. 切削颤振的相位特性研究[J]. 振动工程学报, 2000, 13(4): 510-515.

Fu Lianyu, Yu Junyi, Bao Ming. Study on the phase characteristics of cutting chatter[J].Journal of Vibration Engineering,2000,13(4): 510-515.(in Chinese)

[4] 吴石, 渠达, 刘献礼，等. 轴向铣削力与陀螺效应对颤振稳定域的影响[J]. 振动、测试与诊断, 2013, 33(6): 931-936.

Wu Shi, Qu Da, Liu Xianli, et al. Influence of axial milling force and gyroscopic effect on milling chatter stability[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(6): 931-936.(in Chinese)

[5] 黄强, 张根保, 张新玉, 等. 对再生型切削颤振模型的试验分析[J]. 振动工程学报, 2009, 21(6): 547-552.(in Chinese)

Huang Qiang, Zhang Genbao, Zhang Xinyu, et al. Experimental analysis on regenerative chatter model[J]. Journal of Vibration Engineering, 2009, 21(6): 547-552.(in Chinese)

[6] 吴石, 刘献礼, 王艳鑫. 基于连续小波和多类球支持向量机的颤振预报[J]. 振动、测试与诊断, 2012, 32(1): 46-50.

Wu Shi, Liu Xianli, Wang Yanxin. Chatter prediction based on continuous wavelet features and multi-class spherical support vector machine[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(1): 46-50.(in Chinese)

[7] 杨毅青, 刘强, 王民, 等. 面向车削颤振抑制的多重阻尼器优化设计[J]. 振动工程学报, 2010, 23(4): 468-474.

Yang Yiqing, Liu Qiang, Wang Min, et al. Optimization of multiple tuned mass dampers for chatter suppression in turning[J]. Journal of Vibration Engineering, 2010, 23(4): 468-474.(in Chinese)

[8] Altintas Y, Stepan G, Merdol D, et al. Chatter stability of milling in frequency and discrete time domain[J]. CIRP Journal of Manufacturing Science and Technology, 2008, 1(1): 35-44.

[9] Albertelli P, Cau N, Bianchi G, et al. The effects of dynamic interaction between machine tool subsystems on cutting process stability[J]. International Journal of Advanced Manufacturing Technology, 2012, 58(9-12): 923-932.

[10]Iglesias A, Munoa J, Ciurana J. Optimisation of face milling operations with structural chatter using a stability model based process planning methodology[J]. International Journal of Advanced Manufacturing Technology, 2014, 70(1-4): 559-571.

[11]Zhang Yimin, He Xiangdong, Liu Qiaoling, et al. Robust reliability design of banjo flange with arbitrary distribution parameters[J]. Journal of Pressure Vessel Technology-Transactions of the Asme, 2005, 127(4): 408-413.

[12]O′Connor P D T, Kleyner A. Practical reliability engineering[M]. 5th ed.Chichester: Weily, 2012:19-47.

10.16450/j.cnki.issn.1004-6801.2016.03.012

*国家自然科学基金资助项目(51575094，51135003)；教育部新世纪优秀人才支持计划资助(NCET-13-0103)；中央高校基本科研业务费资助项目(N140304003)

2014-05-22；

2014-09-12

TH112.1

黄贤振，男，1982年6月生，副教授。主要研究方向为机械动态可靠性。曾发表《Reliability-sensitivity analysis using dimension reduction methods and saddlepoint approximations(《International Journal for Numerical Methods in Engineering》2013,Vol.93,No.8)等论文。

E-mail:xzhhuang@mail.neu.edu.cn