采煤机摇臂齿轮传动系统振源定位分析方法*

2016-11-23毛清华张旭辉马宏伟樊红卫

振动、测试与诊断 2016年3期

关键词：摇臂传动系统采煤机

毛清华，张旭辉，马宏伟，邢望，樊红卫

(西安科技大学机械工程学院西安，710054)

采煤机摇臂齿轮传动系统振源定位分析方法*

毛清华，张旭辉，马宏伟，邢望，樊红卫

(西安科技大学机械工程学院西安，710054)

为了研究采煤机摇臂传动齿轮的振动分析方法并进行实机振源定位验证，首先，采用小波分析对采煤机摇臂振动信号进行降噪处理和频谱分析，依据特征频率下的振幅结果确定故障齿轮的啮合频率；然后，通过Morlet小波包络解调分析获取边频带信号频谱特征，依据边频带特征频率下的振幅结果确定故障齿轮的转动频率；最后，对频谱分析和Morlet小波包络解调分析的结果进行综合分析，锁定故障齿轮的准确位置。对一台国产采煤机摇臂齿轮传动系统进行了振动测试与信号分析，结果表明，基于小波分析、频谱分析和Morlet小波包络解调分析相结合的振动分析方法可以实现对采煤机摇臂故障齿轮的准确定位，为强噪声环境下复杂齿轮传动系统的故障快速定位和现场定点维修提供了方法支持。

采煤机；振动测试；小波分析；频谱分析； Morlet小波包络解调

引言

采煤机是煤矿采煤工作面的核心设备之一，其运行状态和振动水平直接影响煤矿生产的经济性和安全性[1-2]。摇臂是采煤机切割煤层的关键动力部件，具有传动链长、齿轮类型多及环境噪声强的特点，给采煤机摇臂的现场故障诊断准确性带来了极大挑战。振动检测方法是机械传动系统故障诊断的良好方法，其主要是通过振动信号的时域和频域特征提取来实现[3-5]。鉴于现代机电设备故障的多元性和耦合特征，在实际故障定位研究中，通常采用多方法联合诊断的思路。文献[6]运用时域波形、峭度指标、细化谱和倒频谱判断机械故障的具体部位，对旋转机械的故障诊断和定位具有较高的准确率。文献[7]运用小波包与倒频谱分析对风电机组齿轮箱的齿轮裂纹故障进行了诊断，实现了故障的准确定位。文献[8]运用经验模式分解和全息谱相结合的方法实现了对转子不平衡的准确诊断。鉴于采煤机摇臂齿轮副多、传动链长且采煤机环境噪声大的特点，对采煤机摇臂传动系统振动特征频率进行理论计算和振动信号分析发现，其振动信号中具有多个齿轮振动特征频率相同、包含大量噪声、振动特征频率出现多次谐波以及特征频率周边具有多个边频带等特点。小波分析是一种良好的信号降噪方法，能有效滤除振动信号中的强噪声，从而有效提取故障信号[9-12]。振动信号的边频带包含着齿轮传动诸多故障信息，目前常用边频带频谱分析方法主要有希尔伯特变换解调分析和Morlet小波包络解调分析两种。Morlet小波包络解调分析相比希尔伯特变换解调分析，可以减少包络检波分析中人为设定滤波中心频率和带宽的影响[13-14]。

为了提高信噪比并准确定位振源，笔者采用小波变换去除采煤机摇臂振动信号中的噪声，运用频谱分析与Morlet小波包络解调分析相结合的方法获得齿轮的故障振动特征频率和转动频率，在此基础上实现采煤机摇臂传动系统振源的准确定位。

1 采煤机摇臂振源定位分析方法

采煤机摇臂齿轮传动系统振动信号分析方法如图1所示。首先，应用小波降噪方法对采集到的振动信号进行降噪处理，对比故障与正常状态下采煤机摇臂振动信号时域均方根值，进行故障预判，当振动信号时域均方根值超过正常振动信号一定范围时进行故障定位。故障定位分以下两个步骤进行：

1) 对降噪后的振动信号进行频谱分析，与正常状态下的频谱分析结果对比，得出故障齿轮振动特征频率，鉴于采煤机传动系统存在多个齿轮振动特征频率相同的情况，这里频谱分析只能初步确定故障可能部位；

2) Morlet小波包络解调分析可以对振动特征频率相同的齿轮族，根据各不同齿轮的转动频率来确定发生故障的准确部位，因此，根据频谱分析与Morlet小波包络解调分析即可完成故障部位的最终确定。

图1 采煤机摇臂故障定位分析流程图Fig.1 Flow chart of shearer ranging arm fault location analysis

2 Morlet小波包络解调分析方法

Morlet小波是一种复数小波，其实部为零相移滤波器和虚部为90°相移滤波器，故运用Morlet小波进行复数小波变换后的小波系数的实部和虚部相位差90°。根据包络检波解调原理可知，当两个信号幅值相同并且相位相差90°时，可通过解调提取幅值分量，且其具有全频带范围内带通滤波器功能。因此，可通过Morlet小波包络解调分析方法获得小波系数中的包络分量。

根据小波变换原理，Morlet小波包络解调的计算过程如下

Wf(a,b)=f(t)*ψa,b(t)=f(t)*ψa,r(t)+

f(t)*jψa，i(t)

(1)

其中：f(t)为实际信号；ψa,b(t)为复Morlet小波函数；ψa,r(t)为复Morlet小波函数实部；ψa，i(t)为复Morlet小波函数虚部。

根据Morlet小波的实部和虚部展开，得出Wf(a,b)的实部与虚部表达式为

(2)

(3)

根据式(2)和式(3)可得小波系数包络分量计算式

(4)

式(4)中Wf(a,b)的实部和虚部可以在时域中根据式(2)和式(3)的卷积计算得出。为了提高计算速度，将其转换到频域用快速傅里叶变换(fast Fourier transformation,简称FFT)，计算公式为

(5)

(6)

根据式(5)和式(6)可得出ψ(t)的傅里叶变换式为

(7)

对式(1)进行傅里叶变换可得

(8)

对式(8)进行傅里叶反变换可得

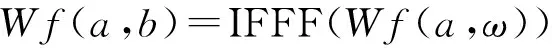
(9)

式(8)和式(9)为其在频域内进行复数小波变换的计算公式。将得到的Wf(a,b)的实部Re[Wf(a,b)]和虚部Im[Wf(a,b)]代入式(4)中，即得小波系数中的包络分量。

3 测试方案和振动特征频率计算

3.1 采煤机摇臂齿轮传动系统振动测试方案

采煤机摇臂如图2所示，振动传感器布置在图中按数字编号给出，振动传感器选用DH186E-IEPE压电加速度传感器，其灵敏度为9.97 mV/(m·s-2)，信号采集选用DH5901手持式振动测试仪。图2中，径向和轴向加速度传感器分别安装在测点1～测点6。

1-电机轴轴向；2-惰轮轴轴向；3-传动二轴轴向；4-电机轴径向；5-惰轮轴径向；6-传动二轴径向图2 振动传感器布置图Fig.2 Vibration sensor layout

3.2 采煤机摇臂齿轮传动系统振动特征频率计算

采煤机左右摇臂为对称结构，摇臂传动系统结构如图3所示，电机转速为1.5 kr/min。根据图3，通过理论计算得出摇臂齿轮转动频率及传动齿轮啮合频率,如表1所示。

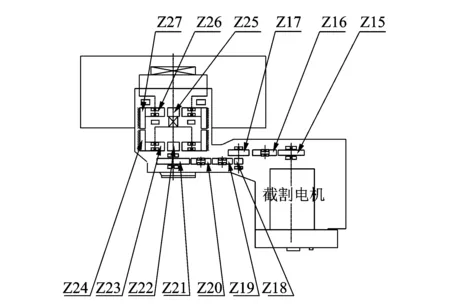
图3 采煤机摇臂齿轮传动系统图Fig.3 Shearer ranging arm gear system

齿轮代号转动频率/Hz啮合频率/Hz齿轮代号转动频率/Hz啮合频率/HzZ1525.00700.0Z2211.81189.0Z1617.95700.0Z237.88189.0Z1717.50700.0Z2400Z1817.50472.5Z252.3642.5Z1914.32472.5Z261.8542.5Z2014.32472.5Z2700Z2111.81472.5

由表1可知，该采煤机摇臂齿轮传动系统中存在多个齿轮具有相同啮合频率的现象。因此，需要通过Morlet小波包络解调分析得出故障齿轮转动频率来实现故障齿轮的准确定位。

4 采煤机摇臂齿轮传动系统振源定位分析

试验时，对某型号采煤机摇臂处于正常状态和故障状态的振动信号进行了采集。测试时，故障摇臂的振动噪声很大，通过对摇臂故障状态的各位置传感器时域信号分析发现，惰轮轴处轴向振动信号的幅值最大，故对惰轮轴的轴向振动信号进行分析。

4.1 时域分析

时域分析主要通过同一位置摇臂实际振动测试信号与摇臂正常状态振动信号的峰值或均方根值对比分析来对故障预判。考虑到实际工作中振动信号峰值特征存在随机因素，笔者采用均方根值作为故障预判指标。根据对该机型摇臂惰轮轴处多次正常状态振动信号均方根值的计算分析发现，正常状态均方根最大不超过17.1 m/s2。

运用小波降噪方法对所采集的振动信号进行降噪，摇臂传动系统正常和故障状态降噪处理后的时域波形如图4所示。根据图4可知，摇臂正常状态下振动信号的幅值最大值和均方根值分别为126.1和12.2 m/s2，故障状态下振动信号幅值的最大值和均方根值分别为718.9和202.9 m/s2，其时域波形均方根值远大于正常状态均方根值的最大值17.1 m/s2。

图4 正常与故障摇臂惰轮轴处振动信号时域波形图Fig.4 Idler shaft vibration signal time-domain waveform of normal and fault ranging arm

因此，通过时域分析，初步预判摇臂齿轮传动系统发生了故障。

4.2 频谱分析

为了对摇臂齿轮传动系统故障部位进行定位，对采煤机正常与故障时的摇臂惰轮轴处时域信号进行FFT分析，得到正常与故障摇臂齿轮传动系统的振动信号频谱分析结果，如图5所示。

图5 正常与故障摇臂惰轮轴处振动信号频谱图Fig.5 Idler shaft vibration signal spectrogram of normal and fault ranging arm

由图5可知，正常摇臂在945 Hz(472.5 Hz的二倍频)处幅值为0.978 m/s2，在1 400 Hz(700 Hz的二倍频)处幅值为0.598 1 m/s2；故障摇臂在945 Hz(472.5 Hz的二倍频)处幅值为28.61 m/s2，在1 418 Hz(700 Hz的二倍频)处幅值为16.24 m/s2。据此数据和表1中理论值对比，摇臂故障部位初定为Z15,Z16,Z17,Z18,Z19,Z20和Z21。

4.3 Morlet小波包络解调分析

图6 正常与故障摇臂惰轮轴处振动信号解调谱Fig.6 Idler shaft vibration signal demodulation spectrogram of normal and fault ranging arm

为了进一步准确定位故障齿轮，需获得齿轮的转动频率。运用Morlet小波包络解调分析对正常和故障摇臂惰轮轴处的振动信号进行解调谱分析，得出正常与故障摇臂振动信号解调，如图6所示。由图可知，在转频17.58和34.96 Hz(17.58 Hz的二倍频)处，正常与故障摇臂惰轮轴处振动幅值分别为0.013 17和0.160 2 m/s2;0.022 73和0.177 9 m/s2，转动频率为17.5 Hz处幅值提高了约12倍，即故障齿轮发生在转动频率为17.5 Hz的齿轮上。由表1可知，转动频率为17.5 Hz的齿轮为Z17和Z18，因此，判定故障发生在齿轮Z17和Z18处。

综合频谱分析和Morlet小波包络解调分析结果，确定摇臂故障齿轮为Z17和Z18。据此，将Z17和Z18齿轮更换，更换后经过测试，摇臂传动系统的振动和噪声大大降低，摇臂恢复正常工作。试验结果表明，基于小波分析、频谱分析与Morlet小波包络解调分析相结合的振动分析方法实现了对采煤机摇臂齿轮故障的准确定位。

5 结束语

针对采煤机摇臂齿轮传动系统的结构和振动特点，提出了一种小波分析、频谱分析与Morlet小波包络解调分析相结合的振源定位分析方法。运用该方法对某采煤机摇臂传动系统的振源部位进行了定位试验。试验结果表明，小波分析、频谱分析与Morlet小波包络解调分析相结合的振动分析方法可以实现对采煤机摇臂传动系统故障部位的准确定位，对采煤机摇臂等长传动链复杂齿轮传动系统的现场故障诊断提供了一种新的有效手段。

[1] 胡俊，张世洪，汪崇建.采煤机故障诊断技术现状及其发展趋势[J].煤矿机械,2008,29(9):8-10.

Hu Jun, Zhang Shihong, Wang Chongjian. Diagnosis of shearer faults and development trend[J]. Coal Mine Machine, 2008,29(9):8-10. (in Chinese)

[2] 钱沛云，陈曦晖，胡晓，等.基于振动信号分析的采煤机摇臂轴承故障诊断研究[J].煤炭科学技术,2014,42(12):89-92.

Qian Peiyue, Chen Xihui, Hu Xiao, et al. Study on bearing fault diagnosis of ranging boom in coal shearer based on vibration signal analysis[J]. Coal Science and Technology, 2014,42(12):89-92. (in Chinese)

[3] 李舜酩,郭海东，李殿荣.振动信号处理方法综述[J].仪器仪表学报,2013,34(8):1907-1915.

Li Shunming, Guo Haidong, Li Dianrong. Review of vibration signal processing methods[J]. Chinese Journal of Scientific Instrument, 2013,34(8):1907-1915. (in Chinese)

[4] 李辉，郑海起，唐力伟．基于倒双谱分析的轴承故障诊断研究[J]．振动、测试与诊断，2010，30(4) :353-356.

Li Hui, Zheng Haiqi, Tang Liwei. Application of bi-cepstrum technique to bearing fault detection[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(4):353-356. (in Chinese)

[5] 张西宁，郭金良，吴吉利.分数阶域滤波在启停车过程转频振动分量提取中的应用[J].西安交通大学学报,2013,47(11):92-96.

Zhang Xining, Guo Jinliang, Wu Jili. Extracting fundamental frequency during rotating machine start-up or shut-down via fractional domain filtering[J]. Journal of Xi′an Jiaotong University, 2013,47(11):92-96. (in Chinese)

[6] 陈珊珊.时域分析技术在机械设备故障诊断中的应用[J].机械传动，2007,31(3):79-85.

Chen Shanshan. Time domain analysis technology used in diagnosis of machinery equipment fault[J]. Journal of Mechanical Transmission, 2007,31(3):79-85. (in Chinese)

[7] 罗毅，甄立敬.基于小波包与倒频谱分析的风电机组齿轮箱齿轮裂纹诊断方法[J].振动与冲击,2015,34(3):210-214.

Luo Yi， Zhen Lijing. Diagnosis method of turbine gearbox gearcrack based on wavelet packet and cepstrum analysis[J]. Journal of Vibration and Shock, 2015,34(3):210-214. (in Chinese)

[8] 刘然，许宝杰.基于EMD和全息谱的设备故障诊断方法研究[J]. 机械科学与技术，2011,30(11):1922-1926.

Liu Ran, Xu Baojie. The study of the equipment failure diagnosis method based on EMD and holospectrum[J]. Mechanical Science and Technology for Aerospace Engineering, 2011,30(11):1922-1926. (in Chinese)

[9] Ales B, Joze F. Determining cracks in gears using adaptive wavelet transform approach[J]. Engineering Failure Analysis, 2010,17:664-671.

[10]赵志宏，杨绍普，刘永强．多小波系数特征提取方法在故障诊断中的应用[J]．振动、测试与诊断，2015,35(2):276-280．

Zhao Zhihong, Yang Shaopu, Liu Yongqiang. Application of feature extraction method in fault diagnosis based on multi-wavelet coefficients[J]. Journal of Vibration, Measurement & Diagnosis，2015,35(2):276-280. (in Chinese)

[11]马伦，康建设，孟妍，等.基于Morlet 小波变换的滚动轴承早期故障特征提取研究[J]. 仪器仪表学报, 2013,34(4):920-926.

Ma Lun, Kang Jianshe,Meng Yan, et al. Research on feature extraction of rolling bearing incipient fault based on Morlet wavelet transform[J]. Chinese Journal of Scientific Instrument,2013,34(4):920-926. (in Chinese)

[12]蒋永华，汤宝平，董绍江.自适应 Morlet小波降噪方法及在轴承故障特征提取中的应用[J].仪器仪表学报,2010,31(12) :2712-2717.

Jiang Yonghua， Tang Baoping， Dong Shaojiang． Denoising method based on adaptive Morlet wavelet and its application in rolling bearing fault feature extraction[J]. Chinese Journal of Scientific Instrument, 2010,31(12):2712-2717. (in Chinese)

[13]张家凡,易启伟,李季.复解析小波变换与振动信号包络解调分析[J].振动与冲击,2010,29(9):93-96.

Zhang Jiafan, Yi Qiwei, Li Ji. Complex analytic wavelet transform and vibration signals envelope-demodulation analysis[J]. Journal of Vibration and Shock, 2010,29(9):93-96. (in Chinese)

[14]梁霖,徐光华.基于自适应复平移Morlet小波的轴承包络解调分析方法[J]. 机械工程学报,2006,42(10):151-155.

Liang Lin, Xu Guanghua. Optimal envelope demodulation method based on adaptive complex shifted morlet wavelet in beafjng diagnosis[J]. Chinese Journal of Mechanical Engineering, 2006,42(10):151-155. (in Chinese)