考虑导弹自动驾驶仪动态特性的H∞导引律

孟克子，周荻

（哈尔滨工业大学航天学院，黑龙江哈尔滨150001）

考虑导弹自动驾驶仪动态特性的H∞导引律

孟克子，周荻

（哈尔滨工业大学航天学院，黑龙江哈尔滨150001）

为拦截机动目标并克服导弹自动驾驶仪动态特性对制导性能的不利影响，提出一种考虑自动驾驶仪动态特性的H∞鲁棒导引律。将综合制导与自动驾驶仪2阶动态特性的3阶线性时变状态方程表示为多面体线性参变系统，应用线性矩阵不等式（LMI）方法设计了具有参数依赖增益的线性状态反馈形式的新型H∞鲁棒导引律，参数依赖增益中的系数是通过求解以LMI为约束的凸优化问题得到的。仿真结果表明：尽管不需要目标加速度的任何信息，新型H∞导引律依然具有较强的鲁棒性，且具有较高的制导精度。

控制科学与技术；导引律；线性矩阵不等式；自动驾驶仪动态特性；H∞控制；鲁棒性

0 引言

由于导弹自动驾驶仪并非理想的环节，导弹产生的过载与由导引律产生的过载指令之间总是会存在延迟的。因此，为了改善制导性能，在设计导引律的过程中应考虑导弹自动驾驶仪的动态特性。尽管实际的自动驾驶仪具有高阶动态［1］，在设计导引律的过程中通常对其进行一定程度的近似［2-10］。其中，1阶环节是对导弹自动驾驶仪最简单的描述。文献［2-4］均将自动驾驶仪描述为1阶惯性环节，文献［2］基于反步法设计了一种三维非线性导引律，文献［3］采用非奇异终端滑模方法设计了一种有限时间收敛导引律，文献［4］基于模糊自适应逼近策略和动态面滑模控制思想，提出了一种新型的拦截导引律。文献［5］将自动驾驶仪建模为含有单零点的1阶动态环节，基于线性二次型追逐逃逸对策提出了最优的拦截导弹制导策略。为了更好地反应自动驾驶仪的暂态响应特性，文献［6］将2阶振荡环节作为自动驾驶仪的参考模型，推导了综合制导与控制的4阶状态方程，设计了一种自适应非线性导引律。文献［7］将观测器应用于文献［6］中设计的自适应非线性导引律中，以估计无法直接测量的反馈量，如高阶的视线角速率导数等。文献［8-10］同样将自动驾驶仪视为2阶振荡环节，分别设计了动态面导引律、自适应动态面导引律和有限时间收敛滑模导引律。事实上，上述考虑自动驾驶仪2阶动态特性的导引律需要估计由目标加速度引起扰动的上界信息。

H∞控制的优势在于其无需外界扰动信息的情况下依然对扰动具有鲁棒性。因此，将H∞控制应用于导引律的设计可以避免估计由目标加速度引起的扰动信息。文献［11-12］通过解析求解Hamliton-Jacobi偏微分不等式（HJPDI）的方法，分别设计了用于平面拦截和空间拦截的非线性H∞导引律。考虑到寻求HJPDI的解并非易事，文献［13］应用类Lyapunov方法设计了具有L2增益性能的鲁棒导引律，它本质上也是一种H∞导引律。文献［14］利用Lyapunov方法推导了三维非线性H∞鲁棒导引律。文献［15］采用可调非线性H∞控制方法设计了一种考虑饱和约束的三维导弹导引律。上述H∞导引律在设计过程中均将导弹自动驾驶仪视为理想环节，并且它们所采用的方法不适于考虑自动驾驶仪的动态特性，尤其是2阶动态特性。

综上，本文拟设计一种考虑导弹自动驾驶仪2阶动态特性的H∞导引律，既可以对导弹自动驾驶仪进行补偿，又可以保证在无需目标加速度信息的情况下依然对目标机动具有鲁棒性。本文推导了综合制导与自动驾驶仪2阶动态特性的3阶状态方程，进而将该状态方程表示为多面体线性参变（LPV）系统［16-17］，结合基于线性矩阵不等式（LMI）的线性H∞控制理论，设计了考虑导弹自动驾驶仪2阶动态特性的H∞鲁棒导引律。本文所采用的方法也不必求解复杂的HJPDI.综合多面体LPV系统表达以及基于LMI的H∞控制方法还未被用于导弹制导问题中。因此，本文可以为导弹导引律的设计提供一种新的思路和方法。

1 考虑自动驾驶仪动态特性的H∞制导问题

平面内目标-导弹相对运动几何关系如图1所示。其中，vT和vM分别表示目标和导弹的速度，φT和φM分别表示目标和导弹的速度方向角，R表示目标-导弹之间的相对距离，q表示导弹-目标视线角。

图1 平面内目标-导弹相对运动几何关系Fig.1 Target-missile engagement geometry in plane

根据图1得到目标-导弹的相对运动方程为

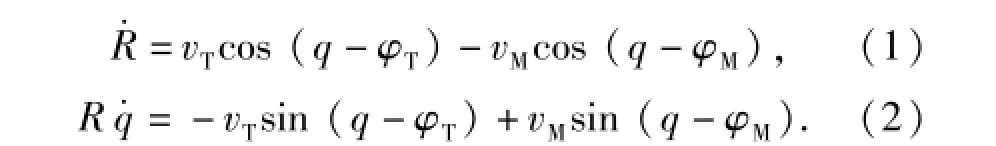
在（1）式和（2）式中，令vR=R·和vq=Rq·.求vR和vq相对时间的1阶导数，可得

式中:aTR和aMR分别表示目标加速度和导弹加速度在视线方向上的分量；aT和aM分别表示目标加速度和导弹加速度在视线法向上的分量。

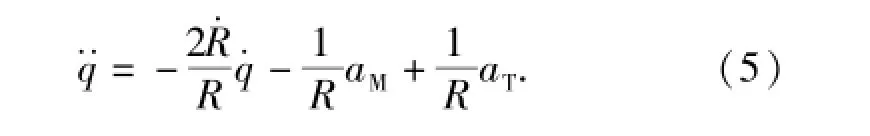
在末制导过程中，通常aMR≡0.设计导引律的关键是保证目标-导弹接近速度vR＜0的条件下确定aM使得视线角速率q·收敛至0或0附近的微小邻域，从而实现准平行接近［8，13］。

将导弹自动驾驶仪动态特性描述为（6）式的2阶振荡环节［6］:

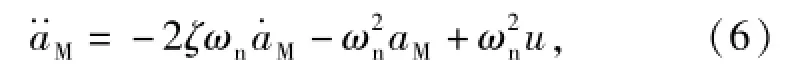
式中:ζ和ωn分别表示近似2阶自动驾驶仪的阻尼比和自振频率；u为对应于aM的制导指令。

下面推导综合制导与自动驾驶仪2阶动态的一体化模型。定义

结合（5）式和（7）式，可得

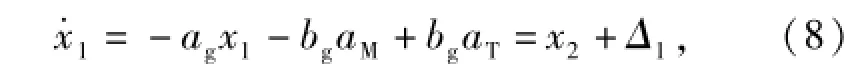
式中:

x2相对时间的1阶导数为

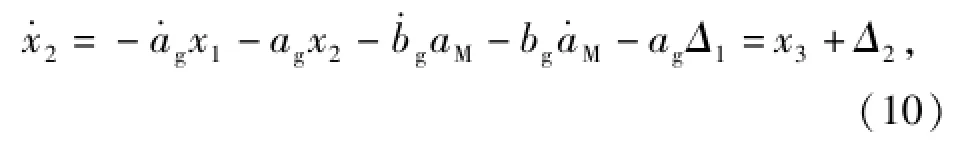
式中:

结合（6）式和（11）式，可以得到x3相对时间的1阶导数为

根据（9）式和（11）式，将aM和a·M表示为关于x1、x2和x3的形式，即

将（13）式和（14）式代入（12）式中，可得

式中:

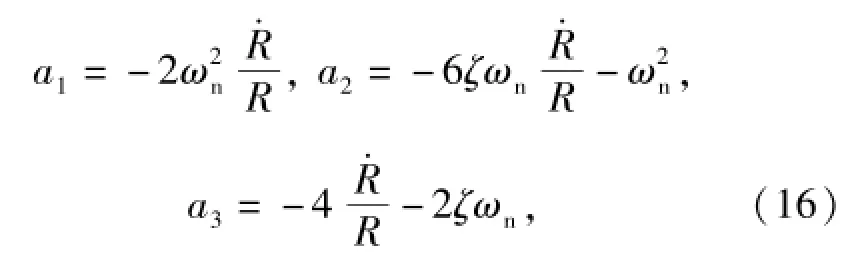
结合（8）式、（10）式、（15）式、（16）式和（17）式得到综合制导与自动驾驶仪2阶动态的一体化模型为

记制导过程结束时刻为tf.令α=1/R，假设1/R（0）=αmin≤α≤αmax=1/σ，其中R（0）表示初始的目标-导弹相对距离，σ为常数，是一个足够小的实数，σ＞0.选取时变参数矢量χ=［χ1χ2］T，其中χ1=（αmax-α）/（αmax-αmin），χ2=（α-αmin）/（αmaxαmin）。显然，对于任意t∈［0，tf］，χ属于集合

将线性时变制导系统控制方程（18）式转化为多面体LPV系统:

式中:

假设扰动信号w满足

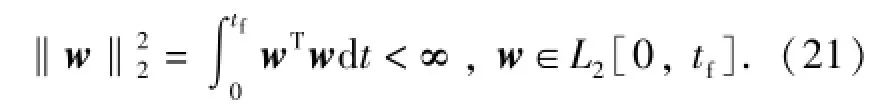
进一步需要指定控制输出信号z.为了保证视线角速率q·尽可能的小。选取控制输出信号

式中:C=［100］；ρ是权衡制导性能和制导指令的权重因数，ρ＞0.H∞导引律设计问题可以归结为确定制导指令u，使得:1）所得的闭环制导系统内稳定，亦即当w=0时，x→0，t→∞；2）当初始条件x（0）=0时，对于任意w∈L2［0，tf］，从扰动w到控制输出z的L2增益小于γ，γ为扰动弱化水平，γ＞0，即

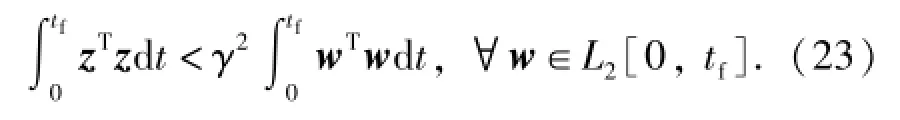
2 考虑自动驾驶仪动态特性的H∞导引律

假设制导指令为线性状态反馈的形式，即

式中:K（χ）∈ℝ1×3表示参数依赖制导增益矩阵。这样，H∞导引律设计的关键在于增益矩阵K（χ）的求解。结合（20）式和（24）式，闭环制导系统可表示为

定理1 对于闭环制导系统（25）式和控制输出信号（22）式，考虑参数依赖Lyapunov函数V（x）= xTP（χ）x，P（χ）=PT（χ）＞0，若不等式

成立，则闭环制导系统（25）式具有H∞性能，即:1）内稳定；2）满足不等式（23）式。

证明 在时间区间［0，tf］上对不等式（26）式两边进行积分，可得

注意到V（x（tf））≥0，由不等式（27）式可以得到

（28）式中，令x（0）=0并结合假设（21）式可得不等式（23）式成立。当w=0时，由不等式（26）式可得这样，闭环制导系统（25）式的内稳定性也得到保证。

下面推导使不等式（26）式成立的参数依赖LMI条件。结合（22）式、（24）式和（25）式，不等式（26）式可表示为

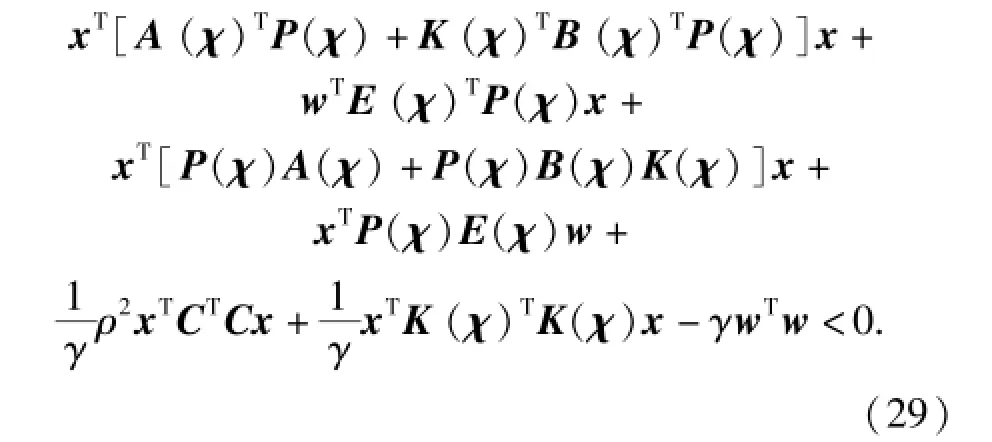
不等式（29）式可以进一步表示为

I表示适当维数的单位矩阵。

显然，如果Φ（χ）＜0成立，则不等式（30）式成立。注意到矩阵不等式Φ（χ）＜0关于矩阵变量P（χ）和K（χ）是非凸的。为将其转化为参数依赖的LMI，对Φ（χ）＜0的两边左乘、右乘矩阵diag｛P（χ）-1，I｝，得

式中:W（χ）=P-1（χ）；Z（χ）=K（χ）W（χ）；V2（χ）= W（χ）AT（χ）+A（χ）W（χ）+ZT（χ）BT（χ）+ B（χ）Z（χ）.

进一步，根据矩阵Schur补性质［16］，将参数依赖矩阵不等式（31）式转化为

至此，考虑导弹自动驾驶仪2阶动态特性的H∞导引律设计问题转化为以参数依赖LMI为约束条件的特征值问题（EVP），即

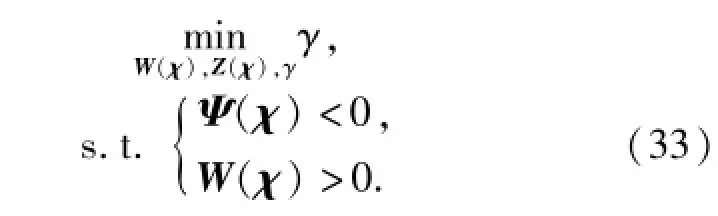
那么，参数依赖制导增益为

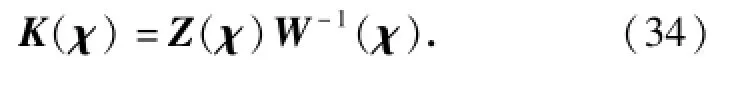
遗憾的是，直接求解EVP（33）式十分困难，因为其中的LMI约束条件是参数依赖的。有效的处理方法是将参数依赖LMI转化为有限个LMI条件。为此，假设参数依赖矩阵变量W（χ）和Z（χ）可以表示为其顶点矩阵的凸组合［17］形式，即式中:Wi、Zi分别表示W（χ）、Z（χ）的顶点矩阵。

对于参数依赖LMI（32）式，根据（35）式中参数依赖矩阵变量W（χ）和Z（χ）的表达，Ψ（χ）可表示为

如果存在矩阵Γij∈ℝ8×8满足

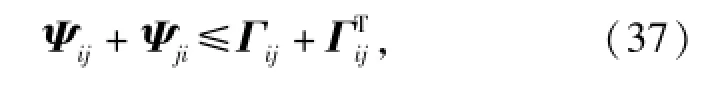
则有

式中:η=［χ1Iχ2I］T.考虑到，可知η≠0.根据（38）式，如果

则有Ψ（χ）＜0.因此，（35）式以及LMI（37）式和（39）式是保证参数依赖LMI（32）式可行的一个充分条件。基于此，EVP（33）式转化为（34）式中的参数依赖制导增益也转化为

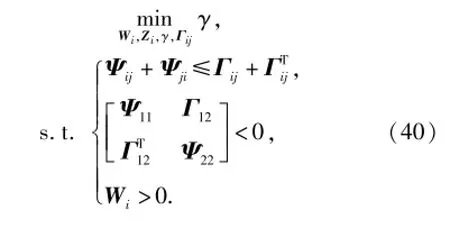
由于导弹的脱靶量（tf时刻的R）很难达到0，因此选择一个足够小的实数σ，满足1/R（0）≤α= 1/R≤1/σ是可以接受的。

实际中目标加速度aT（扰动信号w1）的幅值一定是有限的。尽管扰动信号w2=aT/R和w3=aT/ R2的幅值是随着R的减小而增大的，但二者的幅值在制导过程中依然是有限的［6-7］，另外，制导时间tf也是有限的。因此，（21）式中关于扰动信号w的假设是成立的。

对于制导指令（24）式，K（χ）由（41）式计算得到，其中的系数矩阵Zi、Wi（i=1，2）是在制导开始时通过求解EVP（40）式计算得到的（在操作系统为Windows 7、CPU为3.10 GHz/Intel Core i5的计算机上基于Matlab解算Zi、Wi的时间约为1.8 s，基于C语言的解算时间约为15 ms，在高性能处理器上解算耗时将会更短）。求解EVP（40）式过程中，因为EVP（40）式中的约束条件仅与制导初始条件有关，所以Zi、Wi在整个制导过程中保持不变。参数χ和变量x（见（7）式、（9）式和（11）式）中所含的信息R和q·可以由弹上的主动导引头实时测量得到（对于被动导引头，R可由外部辅助设备测量），aM可以由弹上的加速度计实时测量获得，加加速度可以由aM的测量值基于如（42）式的滤波器实时估计得到。其中，表示的估计值，T表示滤波器时间常数。由此，新型H∞导引律产生的制导指令的更新实时性是可以保证的。

本文H∞导引律的一个特点是会使导弹在初期阶段产生较大的控制过载，目的是让视线角速率快速收敛至0附近的微小邻域。为了约束导弹在制导初期阶段的过载，可以在此阶段加入过载限幅环节。

3 仿真结果

仿真中制导系统采样周期为10 ms.导弹的最大允许过载为30 g.导弹自动驾驶仪动态参数为ζ=0.65，ωn=15 rad/s.滤波器（42）式的时间常数取T=0.01 s.考虑迎头攻击和尾追攻击两种情形验证提出的新型H∞导引律（NH∞G）的有效性，同时，引入自适应滑模导引（ASMG）律［18］:u=进行对比分析。仿真停止的条件是目标-导弹接近速度变号。考虑战斗部作用距离，在仿真停止时刻，将程序中算出的目标-导弹相对位置矢量从惯性系投影到相对速度坐标系，然后将垂直于相对速度矢量的相对距离作为脱靶量。

3.1 迎头攻击情形

导弹的速度vM=1 500 m/s，导弹的初始弹道倾角φM0=25°，弹道偏角ψvM0=0°，导弹的初始位置坐标为xM0=50 km，yM0=10 km，zM0=0 km；目标的速度vT=1 500 m/s，目标的初始弹道倾角为φT0= -2.5°，弹道偏角ψvT0=180°，目标的初始位置坐标为xT0=80 km，yT0=18 km，zT0=0 km.初始的视线角速率为q·（0）=0.112°/s.在NH∞G导引律中，取σ=0.004，ρ=2.在YALMIP［19］软件解析器下采用SeDuMi［20］求解器解算EVP（40）式，得（41）式所示的参数依赖制导增益中的系数矩阵为

以下分别针对目标正弦机动（aT=10cos（πt/3）g）和目标阶跃机动（aT=10 g，t≥5 s）进行仿真:

1）目标正弦机动。此种情况下，在制导初期阶段（t≤3 s），对NH∞G施加10 g的过载限幅。迎头攻击正弦机动目标的仿真结果如图2所示，包括:视线角速率、过载和飞行轨迹，此种情况下目标的过载处于不断变化之中。由于本文提出的NH∞G对导弹自动驾驶仪动态特性进行了补偿，在NH∞G导引下，导弹过载能够迅速响应目标过载的变化，并能够较好地跟踪目标过载的变化过程；而ASMG对目标过载变化过程的跟踪效果相对较差（见图2（b））。因此，NH∞G下的视线角速率在整个制导过程较ASMG下的视线角速率变化更为平稳（见图2（a））。由于两种导引律下导弹的飞行轨迹相似，图2（c））中仅给出了NH∞G下导弹的飞行轨迹。最终，NH∞G和ASMG具有相同的制导时间，NH∞G的脱靶量小于ASMG的脱靶量（见表1）。

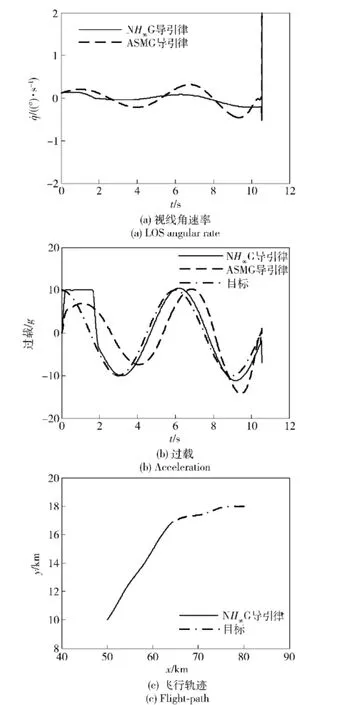
图2 迎头攻击正弦机动目标的仿真结果Fig.2 Simulation results for head-on attack against a sinusoidal maneuvering target

表1 迎头攻击情形下的脱靶量Tab.1 Miss distance for head-on attack scenario

2）目标阶跃机动。此种情况下，在制导初期阶段（t≤3 s），对NH∞G施加5 g的过载限制。迎头攻击阶跃机动目标的仿真结果如图3所示，包括:视线角速率、过载和飞行轨迹。从图3中可以看出，本文提出的NH∞G相比于ASMG能使导弹在初始阶段产生较大的过载响应，使得视线角速度能快速收敛至0，当视线角速率达到稳定以后，导弹过载收敛至目标过载。当t=5 s时，目标突然执行一个向上的常值机动，NH∞G导引下导弹的过载快速响应，跟踪目标过载的变化。视线角速率相较于原来的稳态发生了微小的偏移，但偏移的幅度小于ASMG导引下视线角速率的偏移幅度，并且NH∞G下的视线角速率在最后一刻才彻底发散。最终，NH∞G的脱靶量小于ASMG的脱靶量（见表1），制导时间都为10.56 s.

3.2 尾追攻击情形

导弹的速度vM=1 600 m/s，导弹的初始弹道倾角φM0=5.1°，弹道偏角ψvM0=0°，导弹的初始位置坐标为xM0=50 km，yM0=12 km，zM0=0 km；目标的速度vT=1 000 m/s，目标的初始弹道倾角为φT0= 0°，弹道偏角ψvT0=0°，目标的初始位置坐标为xT0= 60 km，yT0=16 km，zT0=0 km.初始的视线角速率为在NH∞G中，取σ=0.02，ρ=2.求解得W1、W2、Z1和Z2分别为

以下分别针对目标正弦机动（aT=10cos（πt/4）g）和目标阶跃机动（当t＜5 s时，aT=10 g；当t≥5 s时，aT=-10 g）进行仿真。

1）目标正弦机动。此种情况下，在制导初期阶段（t≤3 s），对施加10 g的过载限制。尾追攻击正弦机动目标的仿真结果如图4所示，包括:视线角速率、过载、飞行轨迹。与迎头攻击情形下的仿真结果类似，在NH∞G导引下，导弹过载跟踪目标过载变化过程的效果更好，视线角速率的变化更为平稳。最终，NH∞G的脱靶量仍然小于ASMG的脱靶量（见表2），且NH∞G的制导时间略小于ASMG的制导时间。

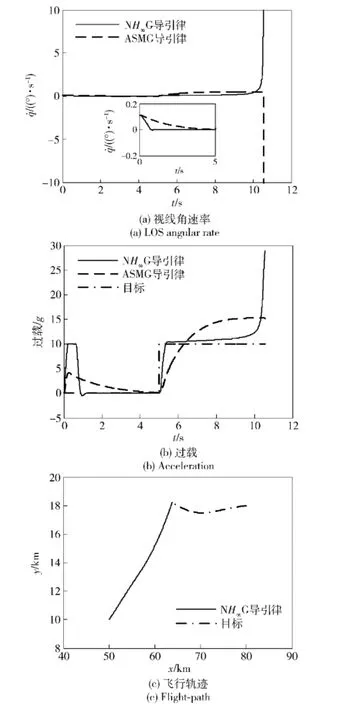
图3 迎头攻击阶跃机动目标的仿真结果Fig.3 Simulation results for head-on attack against a step maneuvering target

表2 尾追攻击情形下的脱靶量Tab.2 Miss distance for tail-on attack scenario

2）目标阶跃机动。此种情况下，在制导初期阶段（t≤3 s），对NH∞G施加14 g的过载限制。尾追攻击阶跃机动目标的仿真结果如图5所示，包括:视线角速率、过载、飞行轨迹。与迎头攻击情形下的仿真结果类似，在NH∞G导引下，导弹过载跟踪目标过载的效果更好，视线角速率更加接近于0.最终，NH∞G的脱靶量仍然小于ASMG的脱靶量（见表2），而从表2中也可以看出NH∞G的制导时间也小于ASMG的制导时间，这一点也体现在图5（a）和图5（b）中。

图4 尾追攻击正弦机动目标的仿真结果Fig.4 Simulation results for tail-on attack against a sinusoidal maneuvering target

最后，考虑一种随机情况。以迎头攻击情形下目标做正弦机动的情况为例，导引头测量的视线角速率包含标准差为0.001 rad/s的白噪声。分别对NH∞G和ASMG两种导引律进行100次蒙特卡洛仿真。其中，NH∞G引起的脱靶量小于0.13 m的概率是100%.而ASMG引起的脱靶量小于0.13 m的概率是35%，小于0.32 m的概率是100%.

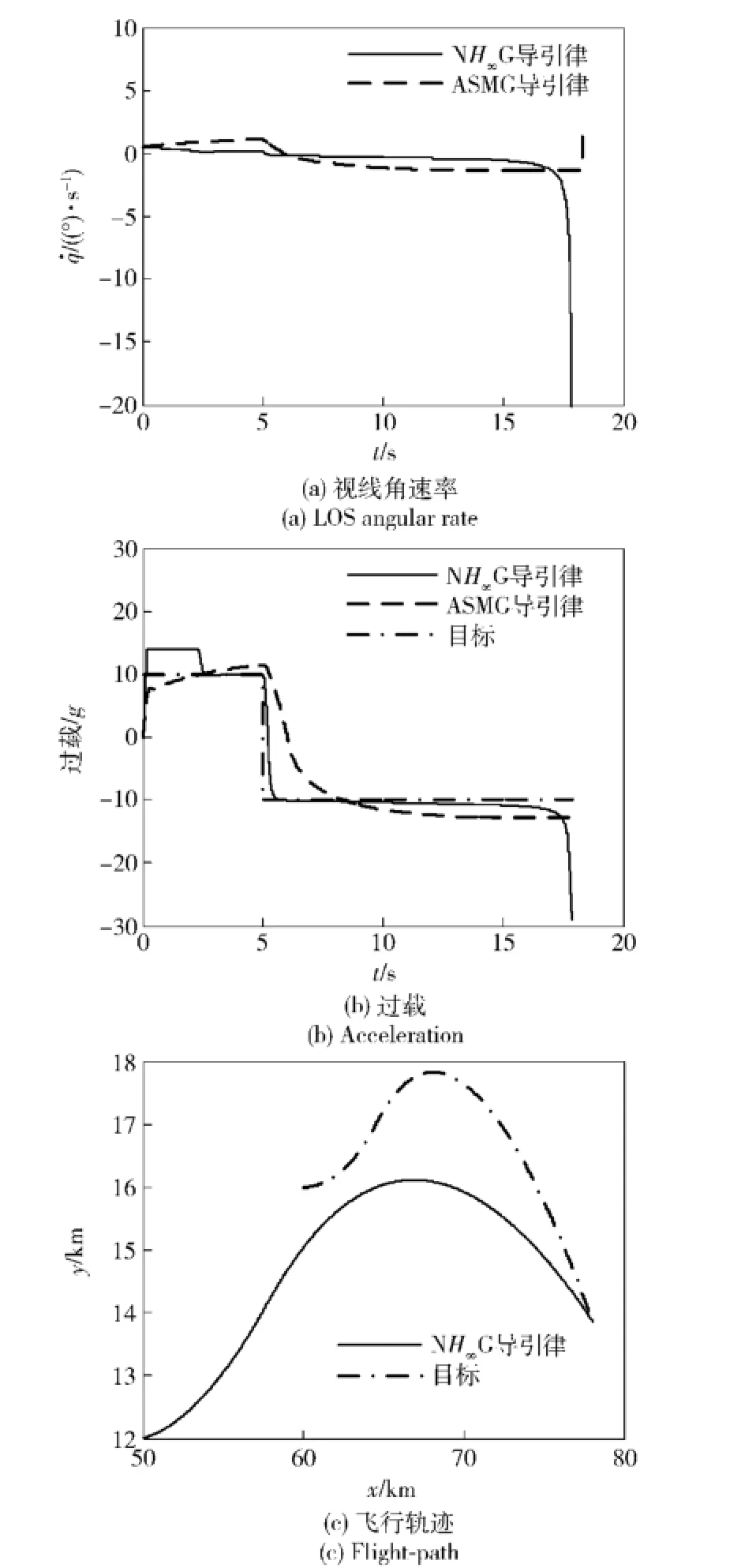
图5 尾追攻击阶跃机动目标的仿真结果Fig.5 Simulation results for tail-on attack against a step maneuvering target

4 结论

本文将基于LMI的多面体LPV系统H∞控制方法应用于考虑导弹自动驾驶仪2阶动态特性的鲁棒导引律设计，得到增益调度线性状态反馈形式的制导指令。本文中提出的导引律不仅形式简单，同时其所需要的制导信息可以通过测量或估计得到，易于实际应用，针对迎头攻击和尾追攻击两种情形对提出的H∞导引律进行了仿真验证，结果表明:在无需目标加速度的任何信息情况下，依然具有较强的鲁棒性，且具有较高的制导精度。

（References）

［1］ Rusnak I，Meirt L.Modern guidance law for high-order autopilot［J］. Journal of Guidance，Control，and Dynamics，1990，14（5）:1056-1058.

［2］ 孙胜，周荻.考虑导弹自动驾驶仪动态特性的三维非线性导引律［J］.宇航学报，2009，30（3）:1052-1056. SUN Sheng，ZHOU Di.Three-dimensional nonlinear guidance law with consideration of autopilot dynamics［J］.Journal of Astronautics，2009，30（3）:1052-1056.（in Chinese）

［3］ Sun S，Zhou D，Hou W T.A guidance law with finite time convergence accounting for autopilot lag［J］.Aerospace Science and Technology，2013，25（1）:132-137.

［4］ 商巍，唐胜景，郭杰，等.考虑自动驾驶仪动态特性的自适应模糊动态面滑模制导律设计［J］.兵工学报，2015，36（4）: 660-667. SHANG Wei，TANG Sheng-jing，GUO Jie，et al.Design of adaptive fuzzy dynamic surface sliding-mode guidance law considering autopilot lag［J］.Acta Armamentarii，2015，36（4）:660-667.（in Chinese）

［5］ Chen R H，Speyer J L，Lianos D.Optimal intercept missile guidance strategies with autopilot Lag［J］.Journal of Guidance，Control，and Dynamics，2010，33（4）:1264-1272.

［6］ Chwa D Y，Choi J Y.Adaptive nonlinear guidance law considering control loop dynamics［J］.IEEE Transactions on Aerospace and Electronic Systems，2003，39（4）:1134-1143.

［7］ Chwa D Y，Choi J Y，Anavatti S G.Observer-based adaptive guidance law considering target uncertainties and control loop dynamics［J］.IEEE Transactions on Aerospace and Electronic Systems，2006，14（1）:112-123.

［8］ 曲萍萍，周荻.考虑导弹自动驾驶仪二阶动态特性的三维导引律［J］.航空学报，2011，32（11）:2096-2105. QU Ping-ping，ZHOU Di.Three-dimensional guidance law accounting for second-order dynamics of missile autopilot［J］.Acta Aeronautica et Astronautica Sinica，2011，32（11）:2096-2105.（in Chinese）

［9］ Xu B，Zhou D.Three dimensional adaptive dynamic surface guidance law accounting for autopilot lag［C］∥2014 American Control Conference.Portland，OR:IEEE，2014:578-583.

［10］ Qu P P，Shao C T，Zhou Di.Finite time convergence guidance law accounting for missile autopilot［J］.Journal of Dynamic Systems，Measurement，and Control，2015，137（5）:051014-1.

［11］ Yang C D，Chen H Y.Nonlinear H∞robust guidance law for homing missiles［J］.Journal of Guidance，Control，and Dynamics，1998，21（6）:882-890.

［12］ Yang C D，Chen H Y.Three-dimensional nonlinear H∞guidance law［J］.International Journal of Robust and Nonlinear Control，2001，11（2）:109-129.

［13］ Zhou D，Mu C D，Shen T L.Robust guidance law with L2gain performance［J］.Transactions of the Japan Society for Aeronautical and Space Sciences，2001，44（144）:82-88.

［14］ 郭建国，周军.基于H∞控制的非线性末制导律设计［J］.航空学报，2009，30（12）:2423-2427. GUO Jian-guo，ZHOU Jun.Design of H∞control based nonlinear terminal guidance law［J］.Acta Aeronautica et Astronautica Sinica，2009，30（12）:2423-2427.（in Chinese）

［15］ Shieh C S.Design of three-dimensional missile guidance law via tunable nonlinear H∞control with saturation constraint［J］.IET Control Theory and Applications，2007，1（3）:756-763.

［16］ Boyd S，Ghaoui L E，Feron E，et al.Linear matrix inequalities in system and control theory［M］.Philadelphia，PA:Society for Industrial and Applied Mathematics，1994:7-18.

［17］ 高会军.基于参数依赖Lyapunov函数的不确定动态系统的分析与综合［D］.哈尔滨:哈尔滨工业大学，2005. GAO Hui-jun.Analysis and synthesis of uncertain dynamic systems based on parameter-dependent Lyapunov function［D］.Harbin:Harbin Institute of Technology，2005.（in Chinese）

［18］ Zhou D，Mu C D，Xu W L.Adaptive sliding-mode guidance of a homing missile［J］.Journal of Guidance，Control，and Dynamics，1999，22（4）:589-594.

［19］ Löfberg J.YALMIP:a toolbox for modeling and optimization in Matlab［C］∥2004 IEEE International Symposium on Computer Aided Control Systems Design.Taipei，Taiwan:IEEE，2004.

［20］ Sturm J F.Using SeDuMi 1.02，A Matlab toolbox for optimization over symmetric cones［J］.Optimization Methods and Software，1999，11（1/2/3/4）:625-653.

H∞Guidance Law Accounting for Dynamics of Missile Autopilot

MENG Ke-zi，ZHOU Di
（School of Astronautics，Harbin Institute of Technology，Harbin 150001，Heilongjiang，China）

In order to intercept the maneuvering targets and overcome the adverse effect of the missile autopilot's dynamics on the guidance performance，this paper aims to propose a H∞robust guidance law with the dynamics of the autopilot considered.The third-order linear time-varying state equation for the integrated guidance and second-order dynamics of autopilot is expressed as a polytopic LPV system.A novel H∞robust guidance law，in the form of linear state-feedback with parameter-dependent gain，is designed using LMI method.The coefficients in the parameter-dependent gain are obtained by solving a convex optimization problem with LMI constraints.Simulation results indicate that，even if the target's acceleration is not known，the H∞guidance law can still achieve strong robustness and obtain high guidance precision.

control science and technology；guidance law；linear matrix inequality；autopilot dynamics；H∞control；robustness

V448.133

A

1000-1093（2016）07-1194-09

10.3969/j.issn.1000-1093.2016.07.006

2015-06-23

国家自然科学基金项目（61174203）

孟克子（1988—），男，博士研究生。E-mail:ljymkz@126.com；

周荻（1969—），男，教授，博士生导师。E-mail:zhoud@hit.edu.cn