基于新息自适应滤波的惯性测量单元误差在线标定方法研究

王洁，熊智，邢丽，戴怡洁，华冰，刘建业

（南京航空航天大学导航研究中心，江苏南京211106）

基于新息自适应滤波的惯性测量单元误差在线标定方法研究

王洁，熊智，邢丽，戴怡洁，华冰，刘建业

（南京航空航天大学导航研究中心，江苏南京211106）

考虑到空天飞行器飞行环境和运动特性下导航传感器误差的噪声统计特性不可能完全精确已知，若使用常规卡尔曼滤波进行在线标定，将会导致滤波精度下降甚至发散。设计一种基于新息自适应滤波方法的惯性测量单元（IMU）误差在线标定方案和算法，克服常规卡尔曼滤波需预先知道噪声统计特性的不足，设计包含IMU安装误差、刻度因子误差和随机常值误差在内的27维高阶状态变量的误差标定模型，分析提出可同时对系统噪声和量测噪声协方差矩阵进行动态调整的新息自适应滤波在线标定算法。仿真验证实验表明，相较于采用常规卡尔曼滤波以及Salychev O自适应滤波算法进行在线标定，所设计的新息自适应滤波在线标定方法能更有效实现对IMU误差的动态标定及补偿，进一步提高了惯性导航系统精度。实物验证实验表明，该方法可有效标定IMU误差残差，提高导航精度，为工程应用带来较大便利。

控制科学与技术；惯性导航系统；惯性测量单元误差；在线标定；自适应滤波

0 引言

空天飞行器的大空域、高机动、多模态飞行特点对导航系统的精度和可靠性提出了极高要求［1］。捷联惯性导航系统作为空天飞行器的核心导航系统，其精度极大地影响着空天飞行器的导航性能。惯性测量单元（IMU）的器件误差模型通常在地面实验室离线标定，但在空天飞行器的高动态飞行过程中，由于高频振动以及不同工作模态间的切换等将引起IMU安装误差及刻度因子误差参数发生变化；此外，随机常值误差亦会随着空天飞行器的长航时飞行而相对于地面离线标定值产生较大差异。考虑到对导航系统重新进行离线标定繁琐的工作量和巨大的时间成本投入，因此非常有必要研究惯性导航系统IMU误差在线标定与补偿技术，这对提高空天飞行器导航系统的精度意义重大［2-4］。

目前，实现IMU误差在线标定的一种有效方法是采用常规的线性扩展卡尔曼滤波技术［5-6］。但是，在采用常规线性扩展卡尔曼滤波技术时，需要预先知道被研究对象的噪声统计特性。在大多数实际情况下，尤其是考虑到空天飞行器复杂多变的飞行环境和运动特性的影响，导航传感器的噪声统计特性不可能完全已知，应用常规线性扩展卡尔曼滤波可能会降低标定精度，甚至造成滤波发散而无法进行误差的有效标定。为了解决这一问题，可以考虑将可动态调整噪声统计特性的自适应滤波运用到IMU误差的在线标定中。目前常用的自适应滤波算法Sage-Husa自适应滤波、Salychev O自适应滤波等，均存在不能同时估计系统噪声和量测噪声协方差阵的问题，不能适用于大多数实际情况［7-13］。因此，本文提出一种可同时动态调整系统噪声和量测噪声协方差阵的新息自适应滤波算法，在建立IMU误差模型、在线标定滤波模型与标定补偿模型的基础上，采用该算法进行IMU误差的在线自适应标定，实现了噪声模型参数不准确情况下IMU误差的动态实时标定与补偿，能有效提高空天飞行器导航系统精度。

图1 在线标定方案总体框图Fig.1 Block diagram of online calibration scheme

1 IMU误差在线标定总体方案设计

基于系统新息进行噪声协方差阵调整的自适应滤波算法，能有效解决噪声模型参数不准确的应用问题，提高空天飞行环境下IMU误差的在线标定精度。为此，本节设计了基于新息自适应滤波的IMU误差在线标定的总体实现方案，如图1所示。

为实现对IMU误差的在线标定，需要建立包含安装误差、刻度因子误差和随机常值误差在内的IMU误差模型，随后通过捷联惯性导航动态误差传播方程建立在线标定滤波模型，利用卫星导航接收机和星敏感器提供位置、速度及姿态外测信息；在对系统新息估计的基础上，分别对系统噪声协方差阵和量测噪声协方差阵进行动态调整与修正，进而估计导航系统状态变量及均方误差，得到IMU安装误差、刻度因子误差以及随机常值误差的在线标定值；利用在线标定值对IMU误差进行补偿，从而提高空天飞行器惯性导航系统精度。

2 在线标定模型

2.1 IMU测量误差模型

在空天飞行器的高动态飞行过程中，由于高频振动以及不同工作模态间的切换等将引起IMU安装误差及刻度因子误差参数发生变化；随机常值误差亦会随着空天飞行器的长航时飞行而相对于地面离线标定值产生较大差异。为了对空天飞行环境下的IMU误差进行有效标定及补偿，建立IMU误差模型为

假设在陀螺和加速度计的安装过程中，任意时刻的安装轴都相互垂直，则陀螺和加速度计的安装

2.2 在线标定滤波模型

选取“东北天”地理坐标系为导航坐标系，载体坐标系为“右前上”。组合导航系统的状态向量选取为惯性导航、陀螺和加速度计的误差状态量，共计27个，包括:3个捷联惯性导航数学平台误差角φE、φN、φU，3个速度误差δvE、δvN、δvU（vE、vN、vU分别为东向、北向、天向速度），3个位置误差δL、δλ、δh（L为纬度、λ为经度、h为高度），3个陀螺随机常值误差参数εbx、εby、εbz，3个加速度计随机常值误差参数，3个加速度计安装误差参数δAx、δAy、δAz，3个加速度计刻度因子误差参数δKax、δKay、δKaz，3个陀螺安装误差参数δGx、δGy、δGz，3个陀螺刻度因子误差参数δKgx、δKgy、δKgz.组合导航系统状态方程为

式中:F为系统矩阵；G为系统噪声系数矩阵；状态矢量X为

式中:φ为平台误差角，δv为速度误差，δp为位置误差。

系统噪声矢量W为

利用卫星导航接收机和星敏感器提供精确的位置、速度及姿态外测信息，采用“位置+速度+姿态”的量测方案，则系统量测方程为

式中:Zp、Zv、Zφ分别为位置、速度及姿态量测矢量，为外测的飞行器位置、速度及姿态信息与惯性导航解算输出的位置、速度及姿态信息之间的差值；Hp、Hv、Hφ为位置、速度及姿态量测系数矩阵，对应的量测噪声矢量为Vp、Vv、Vφ；RM为参考椭球子午圈上各点的曲率半径；RN为卯西圈上各点的曲率半径；Hα为捷联惯性导航数学平台误差角到飞行器姿态误差角（δγ为横滚角误差，δθ为俯仰角误差，δψ为航向角误差）的转换矩阵。

2.3 标定补偿模型

在得到IMU安装误差、刻度因子误差及随机常值误差的标定结果后，暂存标定值，利用标定值对IMU安装误差、刻度因子误差及随机常值误差进行补偿校正，校正在获得IMU原始数据后完成，误差补偿校正算法为

式中:I为单位阵。

3 基于新息自适应滤波的在线标定算法

将2.2节建立的在线标定滤波模型的系统状态方程和量测方程进行离散化处理［14］:

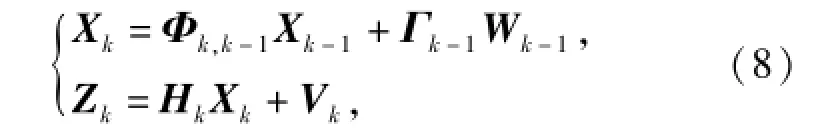
式中:Xk为tk时刻系统状态变量；Xk-1为tk-1时刻系统状态变量；Φk，k-1为tk-1～tk时刻系统的一步状态转移矩阵；Γk-1为tk-1～tk时刻系统噪声系数矩阵；Wk-1为tk-1时刻系统噪声矩阵；Zk为tk时刻的位置、速度及姿态观测量矩阵；Hk为tk时刻量测矩阵；Vk为tk时刻量测噪声矩阵。

从（8）式可以看出，在实现IMU误差在线标定时，需要预先获得系统噪声和量测噪声的统计特性，如果噪声统计特性无法准确获得，将直接影响滤波器性能，进而导致IMU误差标定精度降低，甚至无法进行有效标定。

Salychev O自适应滤波是一种基于新息的自适应滤波算法，其基本原理是在量测噪声协方差阵R设为常阵的基础上，只对系统噪声协方差阵Q进行实时估计和调整的自适应滤波算法。如果系统量测噪声协方差阵R模型参数不准确，必然将影响滤波算法的性能。为此，本文在Salychev O自适应滤波算法的基础上，设计了一种可动态调整系统噪声和量测噪声协方差阵的新息自适应滤波算法，利用该算法进行在线标定，可提高惯性导航系统误差实时估计的准确性与适应性。

3.1 系统噪声协方差阵的自适应估计和调整

滤波新息序列定义为

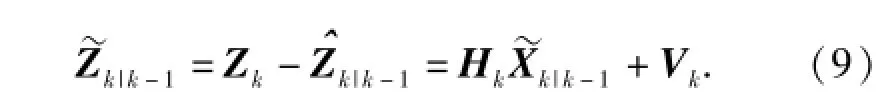
因此，新息序列协方差矩阵可表示为

为了得到新息序列协方差矩阵Ck的具体表达形式，假定为高斯随机过程，依据最大似然估计准则，可以得到的概率密度函数［15］为

似然函数为

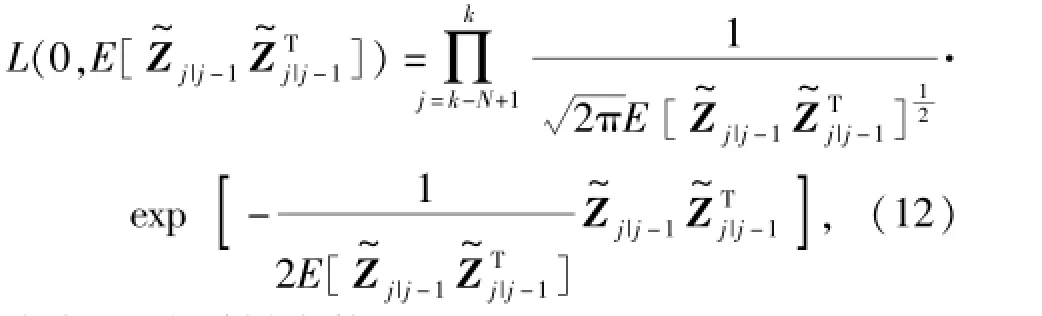
式中:N为采样次数。

（12）式可变换为

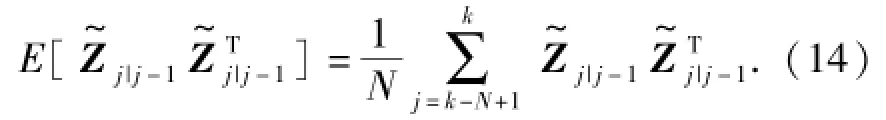
为简化计算，假定N=1.因此新息协方差矩阵可表示成

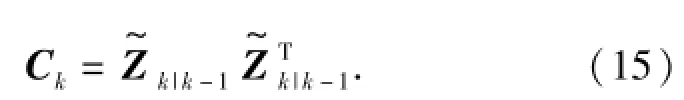
系统噪声协方差阵Qk-1的实时估计为

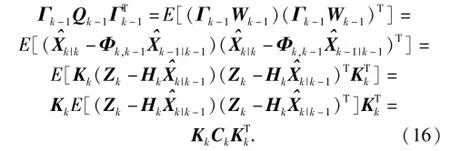
考虑到滤波增益Kk的稳定性和未知性，此处令Kk≈Kk-1.因此，系统噪声协方差阵Qk-1可近似估计为

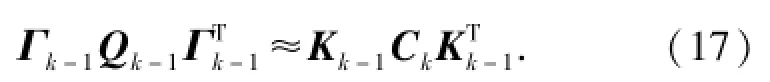
3.2 量测噪声协方差阵的自适应估计和调整

新息序列协方差矩阵可改写成

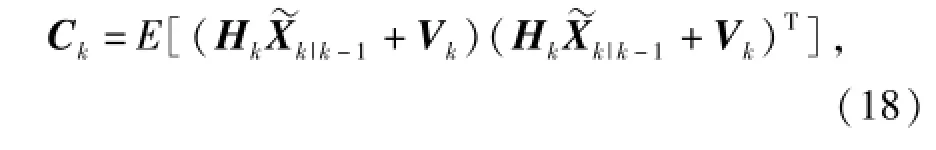
将Rk移至左边，可得量测噪声协方差阵的估计公式为

3.3 基于新息自适应滤波的在线标定算法流程

本文提出的基于新息自适应滤波的在线标定算法可对系统噪声和量测噪声协方差阵进行实时估计与调整，解决了噪声模型参数不准确情况下常规卡尔曼滤波无法进行误差参数精确估计的问题，有效提高了IMU误差的标定精度。该算法流程如图2所示。

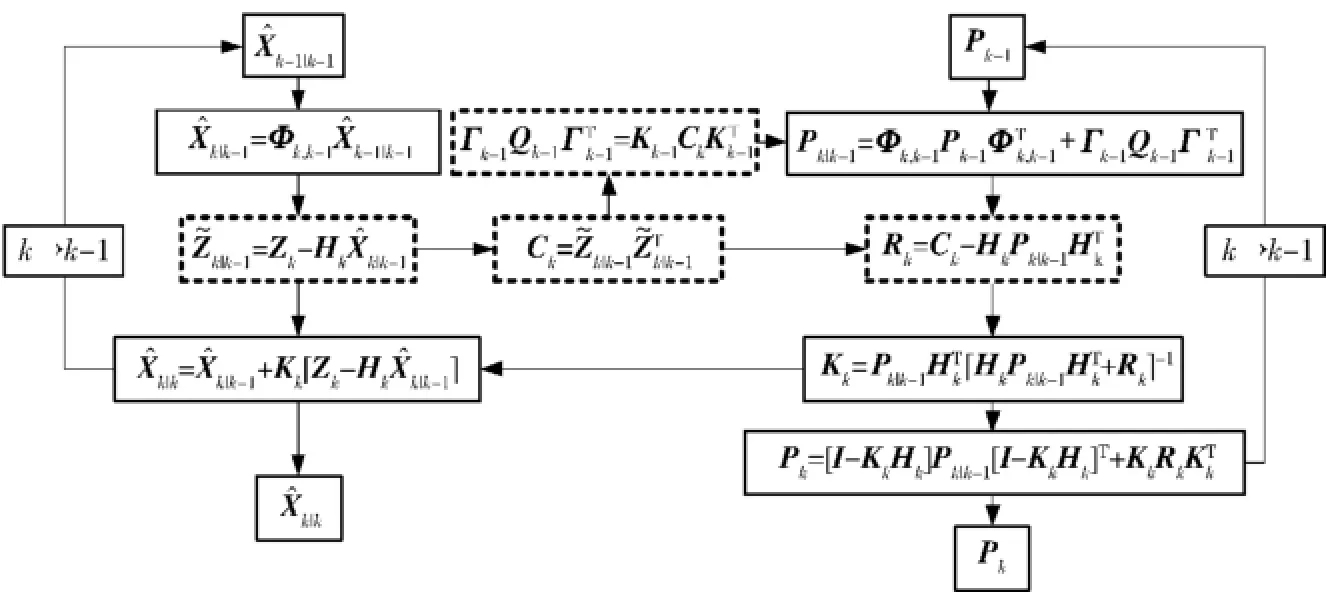
图2 基于新息自适应滤波的在线标定算法流程图Fig.2 Flow chart of online calibration algorithm based on innovation-based adaptive filtering

4 仿真验证

4.1 仿真参数设置

为了验证本文所提出的基于新息自适应滤波的IMU误差在线标定方法的有效性，对比噪声模型参数不准确时，该算法与常规卡尔曼滤波、Salychev O自适应滤波进行在线标定与补偿的仿真结果。仿真中所设定的IMU误差参数如表1所示。

表1 IMU误差参数设置Tab.1 Setting values of IMU error parameters

表2 噪声参数设置Tab.2 Setting values of noise parameters

表3 在线标定与补偿航迹Tab.3 Trace of online calibration and compensation

仿真中系统噪声Q与量测噪声R参数设置如表2所示，其中设置初始参数Q0=diag（0.012，0.012，0.012，10-4g，10-4g，10-4g），R0=diag（0.52，0.52，1.02，0.012，0.012，0.012，（0.001×π/180）2，（0.001×π/180）2，（0.001×π/180）2）。

飞行器初始飞行速度马赫数为1，初始位置为120°E，60°N，高度15.5 km.惯性导航系统解算周期为0.01 s，滤波周期为1 s.在线标定与补偿航迹如表3所示。

4.2 标定仿真结果分析

根据所设计的航迹对IMU误差进行在线标定，两组噪声参数设置情况下的标定曲线分别如图3和图4所示，标定统计结果如表4所示。图3和图4中，点划线代表表1中的误差设定值（简称设定值），实线代表采用本文提出的新息自适应滤波进行标定的误差值（简称新息），虚线代表采用常规卡尔曼滤波进行标定的误差值（简称卡尔曼滤波），点线代表采用Salychev O自适应滤波进行标定的误差值（简称Salychev O）。

图3 第1组标定曲线Fig.3 Calibration curves of Group 1

由图3和图4的仿真曲线和表4的统计结果可以看出，在第1组噪声参数设置情况下，采用本文提出的新息自适应滤波进行误差标定时，其标定精度普遍优于Salychev O自适应滤波及常规卡尔曼滤波。在第2组噪声参数设置情况下，由于噪声误差的进一步增大，在采用Salychev O自适应滤波以及常规卡尔曼滤波进行误差标定时，加速度计安装误差的x轴与z轴不可标，其余误差的标定精度普遍降低；而当采用本文提出的新息自适应滤波进行误差标定时，可实时估计与调整系统噪声与量测噪声协方差的大小，不受噪声模型参数变化的影响。因此在不同的噪声参数设置情况下，采用本文提出的新息自适应滤波进行误差在线标定的标定结果相同。

图4 第2组标定曲线Fig.4 Calibration curves of Group 2

综上可知，在传感器噪声统计特性无法精确已知的情况下，采用本文提出的新息自适应滤波进行误差在线标定，标定精度普遍优于Salychev O自适应滤波以及常规卡尔曼滤波，且噪声误差越大，该算法的优越性越明显。

利用第2组在线标定值对IMU误差进行补偿校正，得到补偿后的惯性导航系统导航误差对比曲线如图5所示，导航误差统计结果如表5所示。图5中，实线代表采用本文提出的新息自适应滤波进行IMU误差补偿修正后的导航误差（简称新息），虚线代表采用常规卡尔曼滤波进行IMU误差补偿修正后的导航误差（简称卡尔曼滤波），点线代表采用Salychev O自适应滤波进行IMU误差补偿修正后的导航误差（简称Salycher O）。

表4 IMU误差标定统计结果Tab.4 Calibrated results of IMU errors

表5 补偿后的惯性导航误差统计结果Tab.5 Compensated navigation errors of SINS

由图5的仿真曲线和表5的统计结果可以看出，采用本文提出的新息自适应滤波算法进行IMU误差的在线标定与实时补偿后，导航姿态误差、速度误差和位置误差普遍较采用常规卡尔曼滤波和Salychev O自适应滤波时有所减小，克服了惯性导航系统在空天领域应用时，传感器噪声统计特性无法精确获取的问题，有效提高了惯性导航系统精度。

5 实物验证

5.1 验证方案设计

以加拿大NovAtel公司的SPAN-CPT光纤/全球定位系统（GPS）组合导航系统作为实验对象（见图6），利用二轴电动转台（见图7）进行静态多位置陀螺和加速度计随机常值误差的离线标定。利用离线标定的结果对IMU误差进行修正，然后将离线标定中未标出的误差通过本文提出的基于新息自适应滤波的在线标定方法进行进一步标定，即在线标定随机常值误差残差。对比离线标定与在线标定两种方法下的标定结果与修正补偿后的导航解算结果，验证本文所提出的在线标定方法确实可以提高导航精度。

5.2 验证结果

通过转台离线标定方法标定出陀螺三轴随机常值误差分别为6.568 377 3°/h、-6.862 176 8°/h和8.709 975 0°/h，加速度计三轴随机常值误差分别为-0.035 088 131 m/s2、0.039 127 719 m/s2和0.018 921 793 m/s2.

由于离线标定仅仅标定了陀螺和加速度计的随机常值误差，因此只对陀螺和加速度计随机常值误差残差的在线标定结果进行了统计。从上述标定结果曲线可以看出，本文所提出的在线标定方法对陀螺和加速度计随机常值误差残差进行了有效标定。

图5 补偿后的惯性导航误差曲线Fig.5 Compensated error curves of SINS

图6 光纤/GPS组合导航系统Fig.6 Fiber/GPS integrated navigation system

图7 二轴转台Fig.7 Two-axis turntable

将陀螺和加速度计随机常值误差残差的在线标定结果进行统计，标出的陀螺三轴随机常值误差残差分别为-0.477 6°/h、-3.308°/h、0.205 4°/h，加速度计三轴随机常值误差残差分别为-0.002 0 m/s2、-0.030 4 m/s2、-0.002 5 m/s2.

图8 IMU随机常值误差残差标定结果Fig.8 Calibrated results of IMU random constant residual errors

图9 补偿后的导航结果曲线Fig.9 Compensated navigation result curves

对比离线标定与在线标定残差补偿修正后的导航姿态、速度、位置解算结果。再将SPAN-CPT光纤/GPS组合导航系统输出的导航姿态、速度、位置结果作为参考，对3种导航结果进行对比，得到图9所示的对比曲线。图9中点划线代表组合系统输出的姿态、速度、位置，实线代表将在线标定所得IMU残差补偿后的姿态、速度、位置解算结果，虚线代表将离线标定所得IMU误差补偿后的姿态、速度、位置解算结果。

从上述对比中，可以清晰地看出将在线标定得到的IMU随机常值误差残差补偿后，解算得到的姿态、速度、位置精度在离线标定的基础上得到了进一步的提升，更接近实际系统输出的参考值，证明该在线标定方法在标定陀螺和加速度计随机常值误差上非常有效。

6 结论

本文提出了一种基于新息自适应滤波的惯性IMU误差在线标定方法。设计了包含IMU安装误差、刻度因子误差和随机常值误差参数在内的IMU测量误差模型，建立了包含27维状态变量的高阶在线标定滤波模型，提出了可动态调整噪声协方差阵的新息自适应滤波算法，基于该算法进行IMU误差的在线标定。通过仿真验证与实物验证，证明了相较于采用常规卡尔曼滤波以及Salychev O自适应滤波算法进行在线标定，所设计的新息自适应滤波在线标定方法能更有效实现对IMU误差的动态标定及补偿，进一步提高了惯性导航系统精度。

本文所研究提出的方法，能够在空天飞行器高动态、长航时飞行过程中实现对惯性IMU误差的动态实时标定及补偿，克服了常规卡尔曼滤波进行在线标定时噪声模型参数不准确的问题，有效提高了惯性导航系统精度。

（References）

［1］ Paez C A.The development of the X-37 re-entry vehicle［C］∥40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Fort Lauderdale，Florida:AIAA，2004:11-14.

［2］ Grewal M S，Henderson V D，Miyasako R S.Application of Kalman filtering to the calibration and alignment of inertial navigation systems［J］.IEEE Transactions on Automatic Control，1991，36（1）:3-13.

［3］ Zhang L D，Lian J X，Wu M P，et al.Research on auto compensation technique of strap-down inertial navigation systems［C］∥International Asia Conference on Informatics in Control，Automation and Robotics.Bangkok，Thailand:IEEE，2009:350-353.

［4］ 彭惠，熊智，王融，等.IMU安装及标度因数误差动态参数辨识方法［J］.中国空间科学技术，2014（1）:42-49. PENG Hui，XIONG Zhi，WANG Rong，et al.The dynamic parameter identification research on the installation errors and the scale factor errors of the IMU［J］.Chinese Space Science and Technology，2014（1）:42-49.（in Chinese）

［5］ 张小跃，张春熹，宋凝芳.基于组合导航技术的光纤捷联系统在线标定［J］.航空学报，2008，29（6）:1656-1659. ZHANG Xiao-yue，ZHANG Chun-xi，SONG Ning-fang.Online calibration of FOG strapdown system based on integrated navigation technology［J］.Acta Aeronautica et Astronautica Sinica，2008，29（6）:1656-1659.（in Chinese）

［6］ Xiong Z，Peng H，Liu J Y，et al.Online calibration research on the lever arm effect for the hypersonic vehicle［C］∥2014 IEEE/ ION Position，Location and Navigation Symposium.Monterey，CA:IEEE，2014:1213-1218.

［7］ Fang J C，Yang S.Study on innovation adaptive EKF for in-flight alignment of airborne POS［J］.IEEE Transactions on Instrumentation and Measurement，2011，60（4）:1378-1388.

［8］ 苏宛新，黄春梅，刘培伟，等.自适应Kalman滤波在SINS初始对准中的应用［J］.中国惯性技术学报，2010，18（1）:44-47. SUN Wan-xin，HUANG Chun-mei，LIU Pei-wei，et al.Application of adaptive Kalman filter technique in initial alignment of inertial navigation system［J］.Journal of Chinese Inertial Technology，2010，18（1）:44-47.（in Chinese）

［9］ Sun F，Zhang H Q.Application of a new adaptive Kalman filitering algorithm in initial alignment of INS［C］∥2011 IEEE International Conference on Mechatronics and Automation.Beijing: IEEE，2011:2312-2316.

［10］ 华冰，刘建业，熊智.联邦自适应滤波在SINS/北斗/星敏感器组合导航系统中的应用［J］.东南大学学报:自然科学版，2005，34（增刊1）:190-194. HUA Bing，LIU Jian-ye，XIONG Zhi.Federal adaptive filtering algorithm research in SINS/Beidou/STAR integrated navigation system［J］.Journal of Southeast University:Natural Science Edition，2005，34（S1）:190-194.（in Chinese）

［11］ Fakharian A，Gustafsson T，Mehrfam M.Adaptive Kalman filtering based navigation:An IMU/GPS integration approach［C］∥2011 IEEE International Conference on Networking，Sensing and Control.Delft，Netherlands:IEEE，2011:181-185.

［12］ Tedaldi D，Pretto A，Menegatti E.A robust and easy to implement method for IMU calibration without external equipment［C］∥2014 IEEE International Conference on Robotics and Automation.Hong Kong，China:IEEE，2014:3042-3049.

［13］ Vijaykumar V R，Vanathi P T，Kanagasapabathy P.Modified adaptive filtering algorithm for noise cancellation in speech signals［J］.Elektronika Ir Elektrotechnika，2015，74（2）:17-20.

［14］ 刘建业，曾庆化，赵伟，等.导航系统理论与应用［M］.西安:西北工业大学出版社，2009. LIU Jian-ye，ZENG Qing-hua，ZHAO Wei，et al.Navigation system theory and application［M］.Xi'an:Northwestern Polytechnical University Press，2009.（in Chinese）

［15］ Salychev O S.Inertial systems in navigation and geophysics［M］. Moscow:Bauman MSTU Press，1998:631-632.

Online Calibration of IMU errors of Inertial Navigation System Based on Innovation-based Adaptive Filtering

WANG Jie，XIONG Zhi，XING Li，DAI Yi-jie，HUA Bing，LIU Jian-ye
（Navigation Research Center，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，Jiangsu，China）

Considering the flight environment and motion characteristics of aerospace vehicle，the noise statistical characteristics of the navigation sensors'errors can't be completely known，which may seriously degrade the filtering precision or even cause filtering divergence if the conventional Kalman Filter is used.An online calibration method for IMU errors of SINS based on the innovation-based adaptive filtering is proposed，which can overcome the weakness of that the conventional Kalman filter should know the statistical characteristics of the system noise and measurement noise in advance.An error calibration model of 27-D high-order state variables is established，including the installation error，scale factor error and random constant error of IMU，and an online calibration algorithm based on the innovation-based adaptive filtering is proposed，which can adjust the covariance matrices of system noise and measurement noise dynamically.Simulation shows that the proposed method performs higher calibration accuracy and better navigation performance compared to the conventional Kalman filter and Salychev O adaptive filte-ring algorithm.It is proved by the field test that this method could calibrate the IMU residual errors effectively，improve the navigation accuracy and bring a great convenience for engineering application.

control science and technology；inertial navigation system；inertial measurement unit error；online calibration；adaptive filtering

V249.3

A

1000-1093（2016）07-1203-11

10.3969/j.issn.1000-1093.2016.07.007

2015-12-03

国家自然科学基金项目（61533008、61533009、61374115）；国家留学基金委资助项目（2012年）；江苏省六大人才高峰资助项目（2013-JY-013）；江苏省高校优势学科建设工程项目（2014年）；中央高校基本科研业务费专项资金项目（NP2015406、NJ20150012、NP20152212、NS2014031）；南京航空航天大学研究生创新基地（实验室）开放基金项目（kfjj20150315）

王洁（1990—），女，硕士研究生。E-mail:wangjie813@nuaa.edu.cn；

熊智（1976—），男，研究员，博士生导师。E-mail:xznrc@nuaa.edu.cn