扭曲尾翼弹箭气动外形多目标优化

陈亮，刘荣忠，郭锐，赵博博，刘磊，杨永亮

（南京理工大学机械工程学院，江苏南京210094）

扭曲尾翼弹箭气动外形多目标优化

陈亮，刘荣忠，郭锐，赵博博，刘磊，杨永亮

（南京理工大学机械工程学院，江苏南京210094）

为了提升掠飞末敏弹战术技术性能，将扭曲尾翼结构应用于弹箭气动布局，并在风洞实验基础上，结合计算流体力学、正交实验、逐步回归分析以及多目标遗传算法，对扭曲尾翼弹箭开展了以增旋、减阻为目标的气动外形多目标优化设计，最终给出了尾翼外形的Pareto优化方案。结果表明：采用扭曲尾翼结构有利于改善弹箭气动性能；所建立的气动参数代理模型，能对弹箭阻力系数和平衡转速进行准确预测，并得到了尾翼几何参数对其影响规律；基于多目标遗传算法最终得到的Pareto优化方案，达到了良好的增旋、减阻效果。该研究方法对扭曲尾翼弹箭气动优化设计具有参考意义。

兵器科学与技术；扭曲尾翼；数值模拟；逐步回归分析；遗传算法；多目标优化

0 引言

掠飞末敏弹以母弹弹体作为稳态扫描平台，利用小射角下弹道平直特性，一边飞行，一边探测目标，具有灵活性强、扫描范围大、不易被反制等优势，这已逐渐成为末敏弹技术研究热点。美国XM943 120 mm炮射掠飞式末敏弹已经完成演示验证［1-2］。为了提高掠飞末敏弹战术技术性能，一方面需要尽可能提高弹箭在飞行过程中的平衡转速，以实现在高速条件下对地面目标的密集扫描，另一方面要求尽可能减小弹箭的阻力系数，以增大射程，扩大打击区域。因此，通过合理的尾翼气动优化设计，使弹箭达到增旋、减阻的效果具有重要意义。

扭曲尾翼是借鉴适用于高转速条件的螺旋桨桨叶结构，提出的弹箭导旋尾翼。目前对该尾翼结构应用于小型弹箭的研究还鲜见报道。文献［3］利用数值方法研究了尾翼扭曲率对弹箭气动特性的影响，但是没有开展相关的实验研究，文献［4］结合叶素理论与四自由度弹道方程，分析了扭曲尾翼弹箭滚转特性，但是尚未对结构参数进行优化；文献［5-6］采用正交实验法，对S-S型和S-C型两种尾翼结构的双翼无伞末敏弹开展了尾翼气动外形优化设计，得到了满足最大阻力系数和最大极阻尼力矩系数的末敏弹尾翼结构；文献［7-8］基于人工神经网络方法建立了优化指标的代理计算模型，并采用多目标遗传算法对飞行器翼型进行了气动外形多目标优化设计，得到了飞行器翼型的Pareto优化方案。而通过优化扭曲尾翼结构参数，以实现弹箭增旋、减阻，提升弹箭的战术技术性能的研究还未见报道。

本文在风洞实验基础上，提出了基于正交仿真实验、逐步回归分析［9］和多目标遗传算法的扭曲尾翼弹箭气动外形多目标优化方法，并分析了尾翼几何参数对阻力系数和平衡转速的影响规律，获得了兼顾减小阻力系数和提高平衡转速的尾翼结构优化方案。

1 风洞实验与数值仿真方法

扭曲尾翼是在平板尾翼基础上，对翼面加以扭曲，使翼面斜置角沿翼展方向逐渐增大的尾翼结构。其尾翼扭曲特性可用扭曲率和平均斜置角表征［3-4］。本文以十字形布局扭曲尾翼弹箭为研究对象，对扭曲率k、平均斜置角θ、翼片面积S以及根梢比λ 4个尾翼几何参数进行优化设计，弹箭基本几何参数如下:直径D为125 mm，尾杆直径为0.48D，翼展为2.8D，翼片厚度为0.024D.

1.1 风洞实验方案

为了研究尾翼扭曲对弹箭气动特性的影响规律，并为优化设计提供参考数据，对扭曲尾翼和平板尾翼两种模型弹箭进行了风洞实验研究。实验模型采用了分块化设计，通过更换尾杆组件可获得不同尾翼结构模型，实验缩比模型零件图如图1所示。

图1 风洞实验零件图Fig.1 Test model parts

实验在某HG-4风洞进行，该风洞为下吹暂冲式闭口高速风洞，实验段尺寸为0.3 m×0.3 m，实验段长度为0.6 m，可用马赫数Ma范围为0.5～4.5.模型通过风洞迎角机构进行支撑和攻角变化，采用6分量应变天平测量模型沿3个坐标轴方向的力和力矩，实验模型安装图如图2所示。实验马赫数Ma为2，攻角α变化范围为-4°～8°，风洞实验方案如表1所示。

图2 风洞实验模型安装图Fig.2 Wind tunnel test setup

表1 风洞实验方案Tab.1 Wind tunnel test schemes

1.2 数值仿真方法

计算流体力学（CFD）是模拟弹箭绕流特性的有效方法，结合风洞实验数据，可以进一步求解分析扭曲尾翼弹箭在高速滚转状态下的气动特性。

仿真采用滑移网格技术模拟弹箭滚转运动，在数值离散时，将流场区域划分为内部绕流区和远场静止区，通过赋予绕流区流场特定转速，实现弹体滚转，两区域在交界面利用插值方法传递数据。仿真过程中，通过求解模型在不同转速下的滚转力矩系数（此处滚转力矩系数特指在当前转速下弹轴方向剩余的力矩系数），插值得出在滚转力矩系数为0时的转速即平衡转速。采用六面体结构网格划分流场，并采用O型网格对附面层进行加密，上游及径向远场长度为24D，下游远场长度为40D，流场网格如图3所示，流场求解采用三维雷诺平均Navier-Stokes方程，湍流模型采用具有较高精度的标准k-ε模型。远场来流采用压力远场条件，壁面采用无滑移边界条件，并取弹箭横截面积为参考面积。

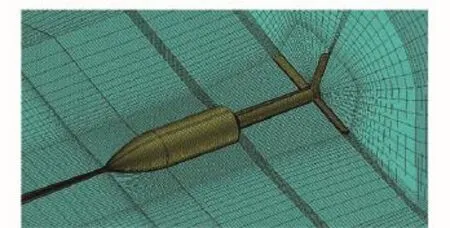
图3 流场网格Fig.3 Grid of flow field

1.3 实验结果与仿真结果对比

为了验证本文CFD方法模拟扭曲尾翼弹箭气动特性的可行性，并分析尾翼扭曲对弹箭气动特性的改善效果，本文按表1所示实验方案进行了仿真计算，并将阻力系数cx和滚转力矩系数mx仿真值与实验值进行对比，结果如图4和图5所示。从图4、图5中可以看出:

1）阻力系数仿真值与实验值变化规律基本一致，均随攻角增大呈非线性增加，在攻角较小时阻力系数仿真值与实验值吻合较好，随攻角增大二者误差有所增加；滚转力矩系数仿真值与实验值接近，且随攻角无明显变化。阻力系数和滚转力矩系数最大相对误差分别为3.7%和4.4%，表明数值方法能较准确求解弹箭气动参数，满足用于气动优化的精度要求。

2）扭曲尾翼模型的阻力系数略大于平板尾翼模型，相对差值最大为1.7%.但扭曲尾翼模型的滚转力矩系数明显大于斜置尾翼模型，当攻角为0°时，滚转力矩系数相对差值约为14.7%.这表明扭曲尾翼模型相对于斜置尾翼模型，在保证阻力系数基本不变的条件下，有效提高了滚转力矩系数，这对实现弹箭增旋、减阻是有利的。

图4 Ma=2时阻力系数随攻角的变化曲线Fig.4 Drag coefficient vs.attack angle for Ma=2

图5 Ma=2时滚转力矩系数随攻角的变化曲线Fig.5 Rolling moment vs.attack angle for Ma=2

图6（a）和图6（b）给出了两种尾翼模型在零攻角下的翼面压力分布仿真结果，其中，竖直位置翼片的右侧为迎风面，左侧为背风面。从图6中可以看出:由于扭曲尾翼翼面斜置角从翼根到翼尖逐渐增大，扭曲尾翼翼面压力沿展向变化较大，而平板尾翼翼面压力分布较均匀，且扭曲尾翼迎风面高压区和背风面低压区较平板尾翼均处于更靠近翼稍处，因此扭曲尾翼能获得更大的滚转力矩。此外，由于尾翼扭曲，在翼稍附近区域扭曲尾翼迎风面和背风面压差大于平板尾翼，而在翼根处相反，在尾翼中部二者压力差接近相等，因此平均而言，在采用了相同的翼面平均斜置角条件下，扭曲尾翼模型与平板尾翼模型阻力系数相差不大，而滚转力矩提升较大。

图6 两种尾翼模型在零攻角下的翼面压力分布Fig.6 Pressure distribution on the empennages of two different empennage models（α=0°）

2 扭曲尾翼优化设计方法

2.1 优化问题数学描述

扭曲尾翼优化设计的目的:调整尾翼几何尺寸组合，提高平衡转速，同时减小阻力系数。该多目标优化问题的数学描述为

目标函数:min cx（X），max ω0（X），

约束条件:ai≤xi≤bi，

其中:设计变量X=［x1，x2，x3，x4］为扭曲尾翼主要几何参数［k，θ，S，λ］；目标函数cx和ω0分别为弹箭阻力系数和平衡转速；ai和bi分别为各几何参数取值上下限。

2.2 代理模型方法

优化过程中，需要计算不同尾翼尺寸组合的阻力系数和平衡转速，如果均采用CFD方法进行模拟

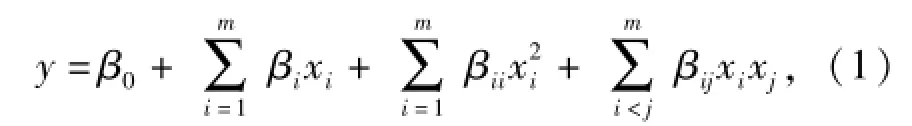
式中:y为输出变量；x为设计变量；β0、βi、βii、βij分别为常数项、线性项、平方项以及交互项系数。

2.3 多目标遗传算法

多目标优化问题求解的关键在于获得问题的非劣解集，即Pareto［12］解。模拟生物进化过程的多目标遗传算法，通过对各优化目标进行权衡折衷，可在一次求解运算中获得问题的多个Pareto最优解，是求解多目标问题的有效方法。基于非支配排序的NSGAⅡ［13］算法是目前应用最为广泛的多目标遗传算法，具有收敛速度快、鲁棒性好、适应性强等特点。该算法基于排序思想，实现个体适应度分配，并通过引入精英保持策略和小生境技术，使遗传种群在进化过程中稳定均匀地逼近真实Pareto前沿。

本文采用多目标遗传算法对扭曲尾翼进行优化设计，通过对代理模型进行寻优，获得尾翼几何参数的Pareto最优解。求解，计算量过大，工程上难以接受。代理模型方法利用有限的仿真样本点，建立设计变量与目标函数间的映射关系，模型结构简单，且能快速准确地对非样本点进行预测计算。在优化设计过程中，用以代替流场仿真，可有效提高优化效率［7］。

为此，本文结合正交实验法和逐步回归分析法，构建扭曲尾翼弹箭阻力系数和平衡转速代理计算模型。首先按照正交实验表安排CFD仿真实验，并利用所得样本数据进行逐步回归分析，建立阻力系数和平衡转速最优回归模型。其中回归方程采用2阶响应面［10-11］形式，可表示为

3 优化实例与结果分析

3.1 阻力系数和平衡转速逐步回归代理模型

对扭曲尾翼4个几何参数各取5个水平，因素水平如表2所示，并按照L25（56）正交表安排CFD仿真实验，结果如表3所示。

表2 因素水平表Tab.2 Levels of factors

表3 正交实验结果Tab.3 Orthogonal experimental results

根据表3正交实验结果，以尾翼几何参数为输入，以CFD仿真结果为输出，进行逐步回归分析，可得扭曲尾翼弹箭阻力系数和平衡转速回归计算模型如下:

阻力系数和平衡转速回归方程决定系数均达到99.5%以上，表明建立的阻力系数和平衡转速逐步回归代理模型具有较高的精度，满足用于优化设计的要求。

3.2 尾翼几何参数对阻力系数和平衡转速的影响

表4给出了逐步回归分析所得各因素的标准回归系数，其绝对值大小表征了各因素对结果相对影响程度。从中可看出:平均斜置角和翼片面积对阻力系数和平衡转速的影响起主导作用，而扭曲率和根梢比的影响次之。此外，在平衡转速回归分析结果中，扭曲率与根梢比交互项k×λ的标准回归系数与根梢比接近，表明其对平衡转速的影响程度与根梢比相当。

为进一步获得阻力系数和平衡转速随各设计变量的变化规律，在初始方案基础上，采用控制变量法，对回归模型进行了求解，得到阻力系数和平衡转速随各因素变化规律，如图7～图10所示。其中，图10考虑了交互项kλ对结果的影响，给出了不同扭曲率下，平衡转速随根梢比的变化规律。

表4 逐步回归分析标准回归系数表Tab.4 Standard regression coefficients

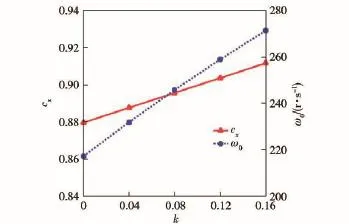
图7 阻力系数和平衡转速随扭曲率的变化规律Fig.7 Drag coefficients and balance rotational speeds vs.twisting rate

图8 阻力系数和平衡转速随平均斜置角的变化规律Fig.8 Drag coefficients and balance rotational speeds vs.mean pitch angle

图9 阻力系数和平衡转速随翼片面积的变化规律Fig.9 Relationship curves of aerodynamic parameters and empennage area

图10 阻力系数和平衡转速随根梢比的变化规律Fig.10 Relationship curves of aerodynamic parameters and taper of empennage

由图7可知:随扭曲率的增加，阻力系数增大，但变化幅度不大，而平衡转速增大显著，这与实验结论相符。由图8、图9可知:阻力系数和平衡转速均随平均斜置角和翼片面积的增加而显著增加，其中阻力系数变化规律接近线性，而平衡转速变化规律具有明显非线性特征。由图10可知:阻力系数随根梢比的增加而减小；由于扭曲率和根梢比的交互作用，平衡转速在扭曲率较小时随根梢比的增加而增大，在扭曲率较大时随根梢比的增加而减小。这表明扭曲率在一定取值范围内，适当增加根梢比，对实现增旋和减阻两个优化目标均是有利的。

综上所述，扭曲尾翼各几何参数对弹箭气动特性的影响具有非线性特性，且对实现增旋和减阻两个优化目标存在矛盾关系，部分参数间交互作用显著，表明在进行优化设计时均不能简单选取各参数最高或最低水平值，而需要设计者在两个设计目标之间进行权衡折衷。

3.3 NSGAⅡ优化结果与分析

针对设计变量对结果影响的复杂性，以平板尾翼实验模型尺寸为初始方案，采用基于非支配排序思想的NSGAⅡ多目标遗传算法对阻力系数和平衡转速代理计算模型进行寻优，取种群规模为200，交叉概率为0.8，变异概率为0.1.

优化结果如图11所示。所得Pareto解均落在正交实验样本点左上方，表明在阻力系数和平衡转速两个指标上均得到了改善，且两指标之间存在矛盾关系，平衡转速越高，阻力系数也越大。表5给出了3种典型优化方案F1、F2、F3与初始方案F0的对比结果。其中:F1的平衡转速与初始方案接近，但阻力系数减小了13.6%；F2的阻力系数与初始方案接近，但平衡转速提高了26.0%；F3是F1与F2的折衷，其平衡转速提高了16.4%，阻力系数减小了6.0%，达到了较好的增旋、减阻效果。在方案决策过程中，应综合考虑转速和射程两方面的需求，在平衡转速满足不遗漏扫描目标要求的前提下，从Pareto最优解中选取阻力系数较小的方案。

图11 Pareto最优解与正交实验结果对比Fig.11 Comparison among Pareto optimal results and orthogonal experimental results

表5 典型优化方案与初始方案对比Tab.5 Comparison of typical optimal scheme and initial scheme

为了验证所得优化结果的正确性，按表5给出的初始方案及3组尾翼优化方案，进行了建模仿真，并将多目标优化模型给出的阻力系数和平衡转速优化值与仿真值进行对比，结果如表6所示。从表6可知:由多目标优化模型给出的阻力系数和平衡转速相对于仿真结果的最大相对误差为3.6%，表明所采用的优化方法具有较高可信度。

表6 优化方案的仿真验证结果Tab.6 Simulated results of optimal schemes

4 结论

1）在马赫数Ma为2的条件下，扭曲尾翼和平板尾翼气动参数仿真结果与风洞实验结果吻合较好，验证了本文数值方法的准确性，同时表明在保证阻力系数基本不变的条件下，扭曲尾翼可有效提高滚转力矩系数，有利于实现弹箭的增旋、减阻。

2）基于正交仿真实验和逐步回归分析，建立的扭曲尾翼阻力系数和平衡转速的代理计算模型，具有较高预测精度；求解得到平均斜置角和翼片面积对弹箭阻力系数和平衡转速的影响起主导作用，扭曲率和根梢比的影响次之，部分尾翼几何参数间交互作用显著；各设计参数对优化结果的影响具有非线性特性和相互制约关系，优化过程中需要进行权衡选择。

3）基于多目标遗传算法，对扭曲尾翼的增旋和减阻性能进行了优化，最终得到典型结构优化方案，并通过CFD方法验证了优化结果的正确性。本文的优化设计方法具有良好的寻优能力，可为扭曲尾翼弹箭气动外形设计提供参考。

（References）

［1］ 吴甲生.制导兵器气动布局与气动特性［M］.北京:国防工业出版社，2008. WU Jia-sheng.Aerodynamic distribution and characteristics of guided weapons［M］Beijing:National Defense Industry Press，2008.（in Chinese）

［2］ Ahn S H，Chang K S.Navier-Stokes computation of Magnus effects on a projectile having differentially spinning sections［J］. Computational Fluid Dynamics Journal，2003，11（4）:440-448.

［3］ 赵博博，刘荣忠，郭锐，等.扭曲尾翼弹箭的气动特性［J］.国防科技大学学报，2014，36（3）:19-24. ZHAO Bo-bo，LIU Rong-zhong，GUO Rui，et al.Aerodynamic characteristics of the twist fin vehicle［J］.Journal of National University of Defense Technology，2014，36（3）:19-24.（in Chinese）

［4］ 赵博博，刘荣忠，郭锐，等.扭曲尾翼弹箭滚转特性［J］.航空动力学报，2015，30（1）:142-148. ZHAO Bo-bo，LIU Rong-zhong，GUO Rui，et al.Rolling characteristics of vehicle with twist fin［J］.Journal of Aviation Power，2015，30（1）:142-148.（in Chinese）

［5］ 吕胜涛，刘荣忠，郭锐，等.S-S双翼末敏弹气动外形优化设计［J］.兵工学报，2013，34（9）:1150-1154. LYU Sheng-tao，LIU Rong-zhong，GUO Rui，et al.Optimum design on aerodynamic shape of the S-S style non-parachute terminal sensitive projectile［J］.Acta Armamentarii，2013，34（9）: 1150-1154.（in Chinese）

［6］ 吕胜涛，刘荣忠，郭锐，等.S-C型双翼末敏弹尾翼结构方案设计［J］.弹道学报，2014，26（2）:6-11. LYU Sheng-tao，LIU Rong-zhong，GUO Rui，et al.Optimum design on aerodynamic configuration of terminal sensitive projectile with S-C style wings［J］.Journal of Ballistics，2014，26（2）:6-11.（in Chinese）

［7］ 张彬乾，罗烈，陈真利，等.飞翼布局隐身翼型优化设计［J］.航空学报，2014，35（4）:957-967. ZHANG Bin-qian，LUO Lie，CHEN Zhen-li，et al.Stealth airfail optimization design of the flying wing［J］.Acta Aeronautica et Astronautica Sinca，2014，35（4）:957-967.（in Chinese）

［8］ 孙伟，张呈林.直升机桨叶气动外形多目标优化设计［J］.航空动力学报，2011，26（7）:1608-1614. SUN Wei，ZHANG Cheng-lin.Multi-objective optimization for aerodynamic shape of helicopter blade［J］.Journal of Aerospace Power，2011，26（7）:1608-1614.（in Chinese）

［9］ 张维刚，廖兴涛，钟志华.基于逐步回归模型的汽车碰撞安全性多目标优化［J］.机械工程学报，2007，43（8）:142-147. ZHANG Wei-gang，LIAO Xing-tao，ZHONG Zhi-hua，et al. Multi-objective optimization on the vehicle impact security based on stepwise regression model［J］.Journal of Mechanical Engineering，2007，43（8）:142-147.（in Chinese）

［10］ Gunst R F.Response surface methodology:process and product optimization using designed experiments［J］.Technometrics，1996，38（3）:284-286.

［11］ Goel T，Vaidyanathan R，Haftka R T，et al.Response surface approximation of Pareto optimal front in multi-objective optimization［J］.Computer Methods in Applied Mechanics and Engineering，2007，196（4）:879-893.

［12］ Jackson I.Convergence properties of radial basis functions［J］. Constructive Approximation，1988，4（1）:243-264.

［13］ Deb K，Pratap A，Agarwal S，et al.A fast and elitist multiobjective genetic algorithm:NSGA-II［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）:182-197.

Multi-objective Optimization on Aerodynamic Shape of Projectile with Twisted Empennages

CHEN Liang，LIU Rong-zhong，GUO Rui，ZHAO Bo-bo，LIU Lei，YANG Yong-liang
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

The twisted empennage structure is applied to the aerodynamic configuration design of hedgehopping terminal sensitive projectile for improving its performance.In order to obtain higher balance rotational speed and lower drag coefficient，a multi-objective optimization design of the aerodynamic shape of projectile with twisted empennages is developed based on the wind tunnel tests.The computational fluid dynamics，orthogonal experiment design，stepwise regression analysis and genetic algorithm are applied，and the Pareto solutions of the empennage shape are provided.The results indicate that the twisted empennage structure can significantly improve the aerodynamic performance of projectile.An aerodynamic parameter surrogate model is established accurately to predict the projectile drag coefficient and balance rotational speed，and the influences of empennage structural parameters on the proposed model can be further obtained.The Pareto solutions based on the multi-objective genetic algorithm display a good performance on the increase in rotational speed and the reduction in drag.

ordnance science and technology；twist empennage；numerical simulation；stepwise regression analysis；genetic algorithm；multi-objective optimization

TJ414+.5

A

1000-1093（2016）07-1187-07

10.3969/j.issn.1000-1093.2016.07.005

2015-11-04

国家自然科学基金项目（11372136）

陈亮（1990—），男，博士研究生。E-mail:studentcl@163.com；

刘荣忠（1955—），男，教授，博士生导师。E-mail:liurongz116@163.com