一种重复二分CSP 4类运动想象脑电信号特征提取算法

郑戍华， 闫琛， 王向周

(北京理工大学 自动化学院， 北京 100081)



一种重复二分CSP 4类运动想象脑电信号特征提取算法

郑戍华， 闫琛， 王向周

(北京理工大学 自动化学院， 北京 100081)

针对脑机接口(BCI)系统中4类运动想象的脑电信号ERD/ERS现象进行研究，提出了一种重复二分共同空间模式(RB-CSP)算法用于4类运动想象脑电信号的特征提取，并运用SVM进行分类研究. 实验结果表明，该方法与传统的4分类CSP扩展算法OVR-CSP相比，减小了算法复杂程度，缩短了信号处理时间，提高了准确率，为在线脑机应用提供了一种新的解决方法.

脑机接口(BCI)；4类运动想象；重复二分共同空间模式(RB-CSP)算法；特征提取

脑机接口(brain computer interface， BCI)是一种不依赖于常规大脑和肌肉信息输出通路的全新的通信系统[1]，其中，特征提取技术是实现BCI的关键，好的特征提取方法有利于BCI系统的稳健性. Muller-Gerking等[2]提出了一种共同空间模式(common spatial pattern， CSP)的特征提取算法，对左、右手两分类想象运动产生的单次EEG数据进行特征提取，3名受试者的分类精确度分别为94%，90%和84%. 随后，CSP逐渐成为运动想象特征提取研究的热点. 在2003年的BCI竞赛中[3]，共同空间模式算法在两分类想象运动特征提取上取得的很多成果证明了其有效性. 目前，BCI系统能实现的信息传输速率较低、实用性较差，因此，BCI系统的模式识别由两类向多类发展. 传统的CSP特征提取方法仅能区分两分类的数据，应用于多类模式必须进行扩展和改进，如一对一CSP[4]，一对多CSP(one versus rest CSP， OVR-CSP)[5]等. Tang等[6-7]采用OVR-CSP对脑电信号进行特征提取，Chin等[4]采用FB-CSP(filter bank common spatial pattern)提取特征， Chen等[8]用基于NeuCube结构的3D脉冲神经网络方法对脑电信号进行特征提取和分类，Talukdar等[9]运用自回归反射系数法提取脑电特征均获得了较高的分类正确率. OVR-CSP把多分类问题的处理转化为多次一类数据对其余所有数据集合的两分类问题，对于N类任务，该方法将N类问题分解为N个一对N-1的两分类问题. 这种算法的优点是其只需要计算N个投影矩阵，缺点是其余的N-1类是个混合的类别，并非同一个类别，它们的数据特征并不相同，难以取得最佳的分类结果. 一对一CSP是把多类数据进行两两区分，转化为多个二分类问题，每两类样本构造一个CSP投影矩阵，然后组合全部的投影矩阵作为多类CSP投影矩阵. 对于一个N类任务的特征提取问题，该方法将N类问题分解为N(N-1)/2个一对一的两分类问题，其优点在于每次构造CSP投影矩阵时，两个类别都是单纯的类别，数据的内部特征统一，更容易计算出差别最大的投影方向，但是需要求N(N-1)/2个投影矩阵，算法复杂度大，需要消耗更多的时间.

针对上述两种算法存在的不足，本文从提高分类正确率和减小算法复杂程度的角度出发，对左手、右手、脚和舌头的4类运动想象脑电信号进行研究，提出了一种基于重复二分CSP(repeated bisection CSP， RB-CSP)和支持向量机(support vector machine， SVM)的运动想象脑电信号特征提取与分类算法.

1 重复二分CSP特征提取原理

1.1 ERD/ERS现象分析

人在做不同的肢体动作或想象运动时，比如左右手拍篮球等动作或想象，对应激活脑区的mu节律(8～13 Hz)会发生能量增强或减弱的现象，这种现象分别被称为事件相关同步(event related synchronization， ERS)和事件相关去同步(event related desynchronization， ERD)[10-11].

根据Rasmussen和Penfield的脑区与肢体对照图并参考文献[10]所做的时频分析可知，在不同运动想象任务下，对C3、CZ、C4电极做短时傅里叶变换(short time Fourier transform， STFT)，可以得到不同时刻的频谱图. 在进行4类运动想象时，ERD/ERS现象在C3、CZ和C4区域的表现如表1所示[10].

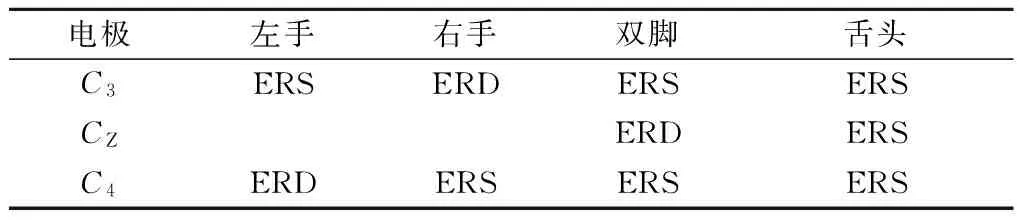
表1 C3、CZ、C4电极的ERD/ERS现象

观察表1可知，对于C3、C4电极来讲，ERD现象仅出现在左手和右手的运动想象中，而没有出现在双脚和舌头的运动想象中；而对于左右手的运动想象，ERD和ERS现象出现在不同的电极，对于双脚和舌头的运动想象，ERD现象仅出现在脚的想象中. 根据这一特点本文提出了一种改进的4分类CSP算法-重复二分CSP(RB-CSP).

1.2 共同空间模式算法(CSP)简介

CSP是针对两类别区分问题提出的一种空间滤波方法，其原理是寻找一个空间滤波器，使两类信号经过滤波器后，最大化一类信号的方差，同时最小化另一类信号的方差，从而区分两类信号. CSP是基于两类信号协方差矩阵的同时对角化来实现的[12]. CSP算法如下：

令Xd，d∈{1，2}表示类别d运动想象模式下的脑电信号，假设已经去除信号的直流成分，则样本归一化的协方差矩阵为

(1)

式中trace() 表示矩阵的迹.

两类的协方差之和为

(2)

式中：Uc为Rc的特征向量矩阵；λc为Rc的特征向量对应的特征值组成的对角矩阵.

白化变换可使方差均匀化，白化矩阵

(3)

协方差矩阵可被白化矩阵W白化

(4)

可以证明S1和S2拥有共同的特征向量，且它们特征值的和为单位矩阵[12]

(5)

投影矩阵为

(6)

原始信号Xi通过Q投影得到新的矩阵

(7)

1.3 重复二分CSP算法

重复二分CSP(RB-CSP)算法的思想是：把运动想象左手和右手的数据看成一类，双脚和舌头的数据看成一类，对于未知运动想象的数据，首先判断是属于左手、右手这一类，还是属于双脚、舌头这一类，然后再细分为4类运动想象中的哪一类. 4类运动想象脑电信号特征提取与分类算法结构如图1所示[13].

在1.2节的两分类CSP算法中，令

(8)

式中XL、XR、XF和XT分别为左手、右手、双脚和舌头的运动想象脑电信号.

由式(5)可知，两个矩阵S1和S2特征值的和总是I，这就意味着，对于同一特征向量，S1对应最大的特征值，就会使S2对应最小的特征值，反之亦然. 若将S1的特征值λ1按从大到小的顺序排列，对应调整特征向量，就会使S2对应的特征值λ2按从小到大的顺序排列.

在式(6)中，选取按特征值大小顺序排列好的特征向量B的前5列和后5列组成新的特征向量B′，则可得到简化的投影矩阵

(9)

原始信号Xi通过Q′投影得到新的矩阵Zi=Q′Xi.

Zi的协方差矩阵计算为

(10)

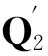
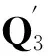
根据特征提取后得到不同的特征向量，再用SVM进行分类.

2 实验数据描述及处理过程

2.1 实验和数据描述

本文算法研究采用BCI2005的datasetsⅢa的实验数据，它包含4类运动想象任务. 脑电信号采样率为250Hz.

2.2 数据预处理

脑电信号采集时，信号和噪声都从各自的源发出，弥散在整个头皮上，使得各个导联信号之间的相关性很强. 因为部分伪迹信号和脑电信号频率重叠，所以简单的频率滤波并不能完全消除脑电信号中的伪迹干扰. 因此，有必要运用公共平均参考法(commonaveragereference，CAR)对原始脑电信号进行预处理，以提高信噪比.

CAR算法能滤除在头皮上均匀分布的噪声，从而能增强特征信息. 其计算公式为

(11)

对BCI2005的data setsⅢa的K3b数据中的某次实验想象左手运动的C3通道进行滤波，滤波效果如图2所示. 可以发现，CAR算法能有效保留信号mu节律的频率成分，即主要的脑电成分，滤除了其他频带的杂波.

以BCI2005的data setsⅢa的K3b数据为例，左手、右手和脚、舌头的训练数据经过预处理后，采用RB-CSP特征提取，得到的归一化特征向量如图3～图5所示；采用OVR-CSP特征提取，得到的归一化特征向量如图6所示.

可以看出，经过RB-CSP算法后的实验数据特征差异性明显，而经过OVR-CSP算法后的特征差异性比较小，所以本文算法的特征使得分类器学习速度更快，分类效果更好.

2.3 分类算法

支持向量机SVM是Vapnik等[14]根据统计学理论提出的一种机器学习方法，是如今研究的热点. 本文选用SVM为分类器来实现4类想象运动特征数据的分类. SVM通过使用非线性映射将输入向量映射到高维特征空间，求取最优分类超平面，使它能够尽可能地将两类数据点分开，同时使分开的两类数据点距离分类面最远，算法如图7所示.

2.3.1 核函数的选择

在脑电信号的分类中，需要将非线性数据映射到高维空间中，这个过程就需要用到核函数，不同的核函数对分类结果有很大影响. 因此本文选择径向基函数作为SVM的核函数实现对脑电信号的特征进行学习和分类处理，其计算公式为

(12)

2.3.2 SVM参数的确定

在使用径向基核函数进行分类时，有两个参数需要确定：C和γ. 其中，惩罚因子C的作用是在确定的特征空间中调节学习机的置信范围和经验风险的比例，核函数参数γ主要影响样本在高维特征空间中分布. 本文采用交叉验证和网格搜索相结合的方法估计C和γ.

3 实验结果分析

本实验包括3个受试者的数据分别为K3b，K6b，L1b. 选取围绕在C3，CZ，C4电极周围的29个通道，分别对每组数据采用交叉验证进行分析和分类，确定准确率. 仿真环境为CPU Intel(R) i3 2.10 GHz， RAM 4 GB， Windows 7， LabVIEW 2011.

3.1 选择最优时间段

为了研究时间不同的数据段对分类正确率的影响，选择4 s的运动想象脑电数据，以2 s为步长，用0.5 s的滑动窗把4 s数据分成5个子数据组，并使用所提算法计算每一段相应的投影矩阵，采用SVM分类器进行分类. 按照脑机接口大赛的要求，根据每个实验者的Kappa系数决定比赛成绩. Kappa系数K的计算方法为

(13)

式中：P为分类准确率；C为类别数.

3个实验者在不同时间段的数据下，平均Kappa系数如图8所示.

图8显示了不同的时间段数据有不同的实验结果. 可以看出，在3.5～5.5 s的时间段内，3个实验者的平均Kappa系数达到了最高. 3个实验者K3b，K6b，L1b分类效果最好的时间段分别为4.5～6.5 s，4.0～6.0 s，3.5～5.5 s. 因此一个合适的时间段对于分类准确率是至关重要的.

同时，以左手运动想象的数据为例，比较经过第一步CSP，左手数据被正确分类到左手和右手这一大类中的准确率，和经过第二步CSP，左手数据被正确分类的准确率，分别如图9，图10所示. 可以明显看出，经过第一步CSP后，左手数据被正确分类到左手和右手这一大类中的平均准确率高达90%以上，证明了算法的有效性.

3.2 分类结果比较

将本文的分类结果与文献[6，15-16]进行比较，如表2所示.t是K3b脑电实验数据特征提取和分类算法所用的总时间；Pmean是4类运动想象的平均分类正确率.

表2 不同实验者的分类结果

Tab.2 Classification result comparison with different subjects and different algorithm

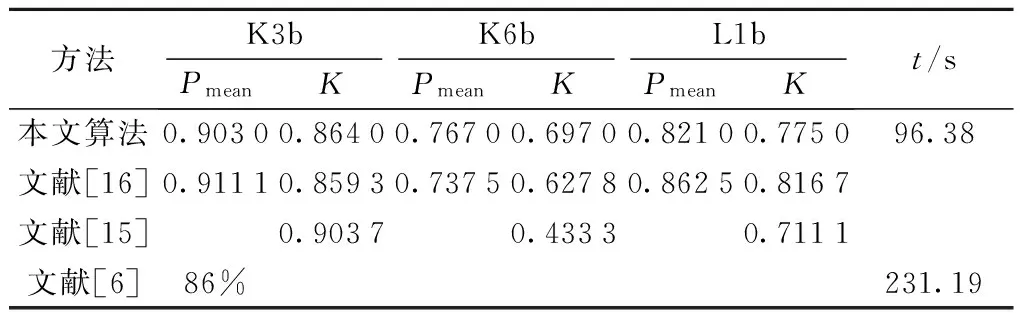
方法K3bK6bL1bPmeanKPmeanKPmeanKt/s本文算法0.90300.86400.76700.69700.82100.775096.38文献[16]0.91110.85930.73750.62780.86250.8167文献[15]0.90370.43330.7111文献[6]86%231.19

与其他文献相比，本文提出的算法不仅分类正确率有了一定程度的提高，而且算法所用时间也有所减少. 与文献[15]，即2005年BCI大赛第2名用的OVR-CSP算法相比，K6b的Kappa值得到了较大的提高. 以K3b为例，在算法复杂程度与时间消耗方面，文献[6]和文献[15]所用的OVR-CSP特征提取算法，在运用本文的预处理前提下，K3b脑电实验数据特征提取和分类算法所用的总时间为231.19 s，而本文算法消耗的总时间仅为96.38 s；同时，本文的RB-CSP算法仅需计算3个投影矩阵，运用3次SVM分类，而OVR-CSP算法则需要计算4个投影矩阵，并运用4次SVM进行分类. 所以，本文算法复杂性明显较低，且时间开销小. 因此，本文的算法适用于实时性要求高的场合，为脑机接口的在线应用打下基础.

4 结 论

本文从脑机接口算法的分类正确率与算法复杂程度的角度，提出了一种基于CSP的4类运动想象改进算法. 该算法与传统的OVR-CSP算法相比，算法复杂度低，时间开销小，且算法分类正确率高. 本文的算法虽然是处理离线数据后得出的，但同样对在线数据的处理有效. 因此在接下来的4类运动想象脑机接口研究中，将着重研究算法的在线应用，朝着BCI系统的实际应用迈进.

[1] Wolpam J R， Birbaumer N， Heetderks W J， et al. Brain-computer interface technology: a review of first international meeting[J]. IEEE Transactions on Rehabilitation Engineering， 2000，8(2):164-173.

[2] Muller-Gerking J， Pfurtscheller G， Flyvbjerg H. Designing optimal spatial filters for single-trial EEG classification in a movement task[J]. Clinical Neurophysiology， 1991，110(5):787-798.

[3] Blankertz B， Theresa M，Schalk V G， et al. BCI competition II[EB/OL].[2002-12-06]http://www.bbci.de/competition/ii.

[4] Chin Z Y， Ang K K， Wang C， et al. Multi-class filter bank common spatial pattern for four-class motor imagery BCI[C]∥Proceedings of Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Minnesota: IEEE， 2009:571-574.

[5] Wu Wei， Gao Xiaorong， Gao Shangkai. One-versus-the-rest (OVR) algorithm: an extension of common spatial patterns (CSP) algorithm to multi-class case[C]∥Proceedings of 2005 27th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. [S.l.]: IEEE， 2006.

[6] Tang Yan， Tang Jingtian， Gong Andong. Multi-class EEG classification for brain computer interface based on CSP[C]//Proceeding of the International Conference on Biomedical Engineering and Informatics. Sanya: IEEE， 2008:469-472.

[7] 王璐，吴小培，高湘萍.四类运动想象任务的脑电特征分析及分类[J].计算机技术与发展，2008，18(10):23-26.

Wang Lu， Wu Xiaopei， Gao Xiangping. Analysis and classification of four-class motor imagery EEG data[J]. Computer Technology and Development， 2008，18(10):23-26. (in Chinese)

[8] Chen Y， Hu J， Kasabov N， et al. NeuCubeRehab: a pilot study for EEG classification in rehabilitation practice based on spiking neural networks[C]∥Proceedings of the 20th International Conference on Neural Information Processing. Berlin Heidelberg: Springer， 2013:70-77.

[9] Talukdar M T F， Sakib S K， Pathan N S， et al. Motor imagery EEG signal classification scheme based on autoregressive reflection coefficients[C]∥Proceedings of 2014 International Conference on Informatics， Electronics & Vision (ICIEV).[S.l.]: IEEE， 2014:1-4.

[10] Wan Baikun， Liu Yangang， Ming Dong， et al. Feature recognition of multi-class imaginary movements in brain-computer interface[C]∥Proceedings of the International Conference on Virtual Environments， Human-Computer Interfaces and Measurements Systems. Hong Kong: IEEE， 2009:250-254.

[11] Pfurtscheller G， Da Silva F H L. Event-related EEG/MEG synchronization and desynchronization: basic principles[J]. Clinical Neurophysiology， 1999，110(11):1842-1857.

[12] Fukunaga K. Introduction to statistical pattern recognition[M]. [S.l.]: Academic Press， 2013.

[13] Bai Xiaoping， Wang Xiangzhou， Zheng Shuhua, et al. The offline feature extraction of four-class motor imagery EEG based on ICA and Wavelet-CSP[C]∥Proceedings of the 33rd Chinese Control Conference. [S.l.]: IEEE， 2014：7189-94.

[14] Vapnik V N. An overview of statistical learning theory[J]. Neural Networks， IEEE Transactions on， 1999，10(5):988-999.

[15] Blankertz B， Theresa M，Schalk V G， et al. Final results of BCI competition III[EB/OL]. http://www.bbci.de/competition/iii/results.

[16] 施锦河，沈继忠，王攀.四类运动想象脑电信号特征提取与分类算法[J].浙江大学学报:工学版，2012，46(2):338-344.

Shi Jinhe， Shen Jizhong， Wang Pan. Feature extraction and classification of four-class motor imagery EEG data[J]. Journal of Zhejiang University :Engineering Science ed， 2012，46(2):338-344. (in Chinese)

(责任编辑：李兵)

A Repeated Bisection CSP Feature Extraction Algorithm of Four-Class Motor Imagery EEG

ZHENG Shu-hua， YAN Chen， WANG Xiang-zhou

(School of Automation， Beijing Institute of Technology， Beijing 100081， China)

In this paper， based on analysis of the phenomenon of ERD/ERS in brain-computer interface (BCI)， an improved repeated bisection common spatial pattern (RB-CSP) algorithm was presented to extract the features of four-class motor imagery EEG and the support vector machine (SVM) was used to classify. The experimental results show that， the proposed algorithm can reduce time consumption and complexity， can produce high classification accuracy， compared with OVR-CSP of the CSP traditional extensions. The proposed algorithm provides a new solution to real-time BCI systems.

brain computer interface (BCI); four-class motor imagery; repeated bisection common spatial pattern (RB-CSP) algorithm; feature extraction

2015-05-08

高校2015年度常规引智资助项目(C2015033)

郑戍华(1976—)，女，博士，讲师，E-mail：zhengshuhua@bit.edu.cn.

王向周(1965—)，男，博士，教授，E-mail:wangxiangzhou@263.net.

TN 911.7

A

1001-0645(2016)08-0844-07

10.15918/j.tbit1001-0645.2016.08.013