锚杆刚度对桩的作用分析及应用
2016-11-22董兴强惠学斌张增魁
董兴强, 惠学斌, 张增魁
(攀钢集团设计研究院有限公司, 四川攀枝花 617000)
锚杆刚度对桩的作用分析及应用
董兴强, 惠学斌, 张增魁
(攀钢集团设计研究院有限公司, 四川攀枝花 617000)
文章分析了锚杆刚度、土体刚度,提出了三个假定,计算了四个桩锚结构,得到了是否考虑锚杆刚度,不影响桩的内力分布,只影响数值的大小。建议在桩上不采用相对集中设锚杆的形式。
岩土工程; 锚杆; 桩; 刚度
在边坡支挡、滑坡治理、基坑支护的结构方案选择中,在某些条件下采用桩锚结构是合适的。在桩锚结构中,对于静定结构,锚杆的刚度对桩没有作用。而在实际工程中,桩锚结构一般都为超静定结构,此时,锚杆的刚度对桩就有作用。在现实的工程中,一般认为锚杆的刚度为无穷大(即锚杆为刚体)。这个假定,在某些结构中产生的误差工程可以承受;但在某些结构中产生的误差工程又不能承受,从而导致工程事故。根据对某些工程事故分析,有必要分析锚杆刚度对桩的作用,以消除工程设计中的隐患。
1 锚杆的刚度、土体的刚度
锚杆的刚度就是锚杆的抗拉刚度。桩锚形成后,锚杆由钢筋或钢绞线、水泥(砂)浆或锚杆粘结剂和土体组成。锚杆的刚度就由钢筋或钢绞线的刚度、水泥(砂)浆或锚杆粘结剂的刚度及土体的刚度组成。准确的锚杆刚度应该是在锚杆形成后的现场测量值。下面分析一下锚杆的受力状态,提出锚杆刚度的假定。桩锚形成后,什么时候产生水平力是无法知道的,也就是说在桩锚寿命内,只要桩锚不垮塌,水平力何时产生是无法知道的,也没有必要知道。因此,锚杆是否受力,也是无法知道的。但是,我们设计的锚杆是按现行理论方法计算的。根据设计的锚杆,锚杆应力最大达钢筋极限应力的0.4倍,而钢筋的极限应变为0.05~0.1,那么,锚杆在设计时的应变为0.02~0.04。水泥(砂)浆的抗拉极限应变为0.000047。在设计状态下,水泥(砂)浆的抗拉变形远小于钢筋的变形。也就是说,在设计状态下,水泥(砂)浆已经断成了一段一段的,而这一段一段的圆环体对钢筋的约束作用就很小了。土体是经过水泥(砂)浆对钢筋产生约束,既然水泥(砂)浆对钢筋的约束都很小了,土体对钢筋的约束作用就更小了。土体抗拉极限应变几乎为零,因此,土体的抗拉刚度对锚杆的约束几乎为零。综上所述,提出假定一:锚杆的抗拉刚度由钢筋或钢绞线决定,不考虑水泥(砂)浆抗拉刚度及土体抗拉刚度的影响。
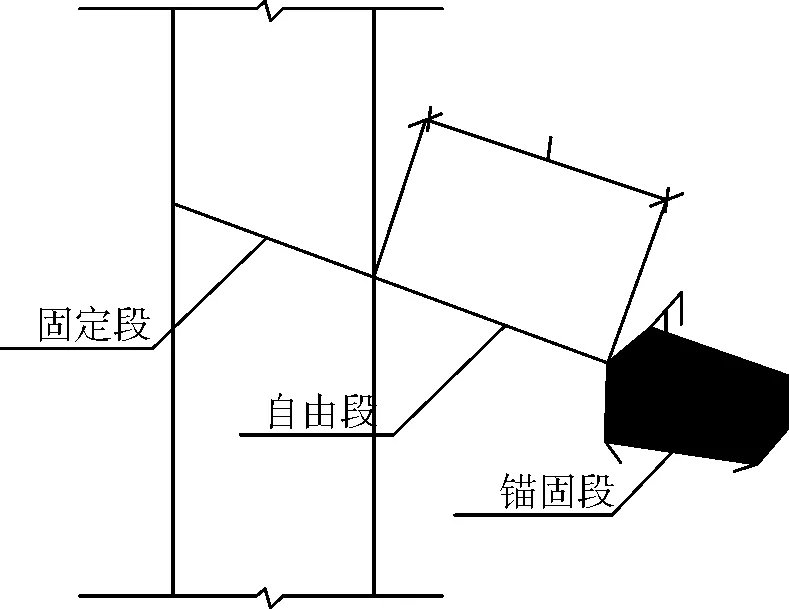
图1 锚杆的组成
锚杆:一般由锚固段、自由段及固定段组成(图1)。在设计状态下,自由段的钢筋或钢绞线各截面所受的力相等。钢筋或钢绞线在锚固段内逐渐将力传给了锚固体。一般情况下,锚固体为岩石,而岩石的抗拉刚度很大,抗拉强度又较小,但是它的体量较大,只要锚杆不被拔出,锚固体的抗拉刚度就很大。钢筋或钢绞线在锚固段内的内力是逐渐减小的,因此,钢筋或钢绞线在锚固段内具有一定抗拉刚度。同理,钢筋或钢绞线在固定段内具有一定的抗拉刚度。为了简化计算,提出假定二:锚杆的抗拉刚度只考虑自由段的锚杆刚度,不考虑锚固段、固定端的锚杆的抗拉刚度。
锚杆抗拉刚度计算:假设锚杆钢筋或钢绞线的面积为A,弹性模量为E,自由段的长度为l,则锚杆的抗拉刚度(K)为:
(1)
桩埋在土体内,无论桩端是简化为嵌固端,还是简化为简支端,土体是有弹塑性的。土体的弹性较小,塑性较大。也就是土体在桩的作用下,不可恢复的变形较大。但是,只要土体不被破坏,土体对桩就有被动约束。土体受压的本构关系已经掌握,但桩端土体的体量还未掌握。因此,桩端土体的刚度还有待于进一步研究,本文为了简化计算,提出了假定三:桩端土体为刚体。
2 下端嵌固、上部一排锚杆的锚杆内力计算
下端嵌固、上部一排锚杆的桩锚结构内力计算的结构计算简图见图2。
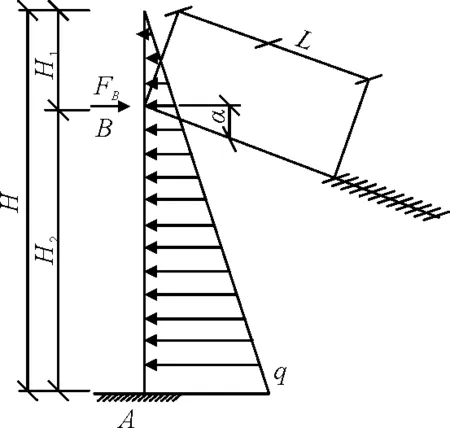
(a)水平力分布为三角形

(b)水平力分布为均布图2 下端嵌固、上部一排锚杆的内力计算简图
(1)计算水平力分布为三角形的锚杆的内力,见图2(a)。将锚杆用FB代替,那么,锚杆所受的力(记为Fm)为:
(2)
在力Fm作用下,锚杆产生的位移(记为ΔmB)为:
(3)
在力Fm作用下,锚杆在支座B处产生的水平位移(记为ΔmBs)为:
(4)
将式(2)、式(3)代入式(4)并整理得:
(5)
FB在支座B产生的位移(记为ΔF)为:
(6)
式中:E为桩的混凝土弹性模量;I为桩的截面惯性矩(下同)。
三角形荷载在支座B产生的位移(记为Δq)为:
(7)

根据支座反力与外荷载在B点处产生的位移等于锚杆的伸长位移,有下式:
(8)
将式(5)、式(6)、式(7)代入式(8)并整理后得:
(9)
从式(9)可以看出,锚杆的抗拉刚度越大,锚杆的内力就越大,最大值为锚杆为刚体时的内力。桩的抗弯刚度越大,锚杆的内力就越小,若桩的抗弯刚度为无穷大,锚杆的内力为零。经过试算,当H=10 m,H1=1 m,H2=9 m,锚杆为3φ25,自由长度为20 m,桩径为800 cm ,混凝土强度等级为C30时,FB=102.7q。该值是把锚杆当成刚体时的锚杆内力85.6%。因此,当不考虑锚杆刚度时,其计算误差接近工程误差,有可能导致工程事故。在这个桩锚结构中,设计时把锚杆内力算大了,锚杆是安全了,势必将桩的内力要算小了。因此,在这个桩锚结构中的破坏是桩身的破坏。
(2)计算水平力分布为均布的锚杆内力,见图2(b)。将锚杆用FB代替,那么,FB在B点产生的位移(记为ΔF)为:
(10)
均布荷载在B点产生的位移(记为Δq)为:
(11)
根据支座反力与外荷载在B点处产生的位移等于锚杆的伸长位移,有下式:
(12)
将式(5)、式(10)、式(11)代入式(12)并整理后得:
(13)
从式(13)可以看出,锚杆的抗拉刚度越大,锚杆的内力就越大,最大值为锚杆为刚体时的内力。桩的抗弯刚度越大,锚杆的内力就越小,若桩的抗弯刚度为无穷大,锚杆的内力为零。经过试算,当H=10 m,H1=1 m,H2=9 m,锚杆为3φ25,自由长度为20 m,桩径为800 cm ,混凝土强度等级为C30时,FB=381q。该值是把锚杆当成刚体时的锚杆内力83.6%。该比例比三角形荷载分布的比例还小。这说明,滑坡治理采用这个结构计算的误差更大。
锚杆的内力得到了,桩的内力也就得到了,故不必计算桩的内力。
3 下端铰支、上部两排锚杆的锚杆内力计算
下端铰支、上部两排锚杆的桩锚结构内力计算的简图见图3。
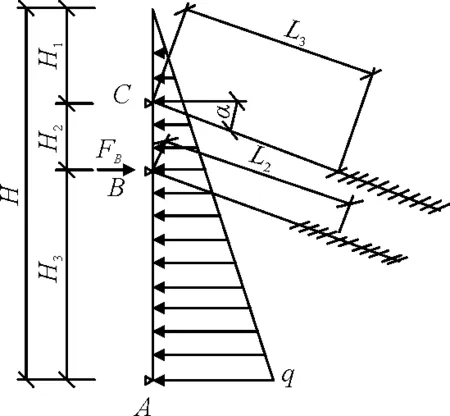
(a)水平力分布为三角形
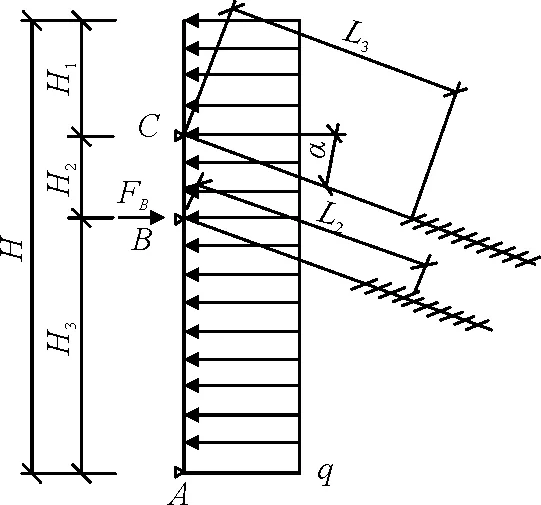
(b)水平力分布为均布图3 下端嵌固、上部两排锚杆的内力计算简图
(1)计算水平力分布为三角形的锚杆的内力,见图3(a)。将B点的支座取消,用FB代替,C点的支座也是由于锚杆的刚度产生位移(记为ΔmCs),根据式(5)有:
(14)
式中:KC为C点处锚杆的抗拉刚度(下同)。同理,FB由于锚杆刚度在B点产生的位移(记为ΔmBs)为:
(15)
由于C点的锚杆刚度在FC作用下在B点处产生的位移(记为Δmbcs)为:
(16)
由于C、B点的锚杆刚度在FC、FB作用下在B点处产生的总位移(记为Δmbzs)为:
(17)
FB在B点产生的位移(记为ΔFB)为:
(18)
三角形荷载在支座B产生的位移(记为ΔqB)为:
(19)
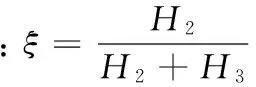
(20)
将式(17)、式(18)、式(19)代入式(20)并整理后得:
(21)
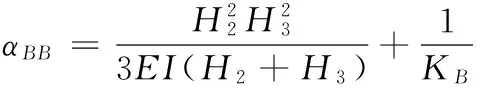
式(21)中有两个未知数FB、FC,因此,由式(21)还不能求解得到FB。以A点(图3(a))为圆心,使FB、FC、q对A点取矩,建立平衡方程,整理后得:
(22)
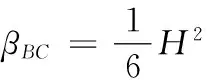
将式(21)与式(22)组成方程组,求解,得:
(23)
式中A=αBBαCC-αBCαCB;AB=αCCβB-αCBβC;AC=αBBβC-αBCβB。
式(23)的关系更复杂。经过试算,当H=10 m,H1=1 m,H2=9 m,锚杆为3φ25,自由长度为20 m,桩径为800 cm ,混凝土强度等级为C30时,FB=4.08q,FC=-3.01q。这样就能求得桩的内力了。从这个结果可以看到,是否考虑锚杆刚度,不影响这个结构的桩的内力分布。设锚杆C,不但无利,还有害。
(2)计算均布荷载桩锚结构的内力,见图3(b)。 将B点的支座取消,用FB代替,C点的支座由于锚杆的刚度产生位移同前。FB在B点产生的位移(记为ΔFB)见式(18)。均布荷载在支座B点产生的位移(记为ΔqB)为:
(24)
根据FB反与q在B点处产生的位移等于锚杆刚度在B点产生的位移,见式(20)。
将式(17)、式(18)、式(24)代入式(20)并整理后得:
(25)
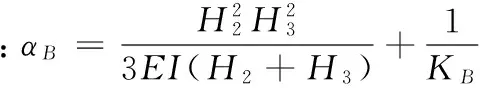
式(25)中有两个未知数FB、FC,因此,由式(25)还不能求解得到FB。以A点(图3(b))为圆心,对FB、FC、q对A点取矩,建立平衡方程,整理后得
(26)
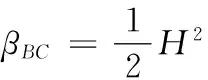
将式(25)与式(22)组成方程组,求解,得:
(27)
式中:A=αBBαCC-αBCαCB;AB=αCCβB-αCBβC;AC=αBBβC-αBCβB。
式(27)的关系更复杂。经过试算,当H=10 m,H1=1 m,H2=9 m,锚杆为3φ25,自由长度为20 m,桩径为800 cm,混凝土强度等级为C30时,FB=0.0658q,FC=-0.00297q。这样就能求得桩的内力了。从这个结果可以看到,是否考虑锚杆刚度,不影响这个结构的桩的内力分布。设锚杆C,不但无利,反而有害。
经过对两排锚杆的桩锚结构分析,发现上排锚杆不但无利,还有害。因此,笔者建议在桩上不采用设两排锚杆的桩锚结构。
4 结束语
通过对几个桩锚结构的受力分析,在假定的条件下,是否考虑锚杆,不影响桩的内力分布,只影响数值变化。经过 对两排锚杆的桩锚结构分析,发现上排锚杆不但无利,还有害。因此,建议不采用在桩上设两排锚杆的桩锚结构。对于特殊结构在没有进行内力分析的情况,不要盲目的取与实际误差太大(所取计算简图可能不知道误差的大小)的假定,使计算结果尽量与实际相符。
[1] 同济大学数学教研室. 高等数学下册[M].第4版. 高等教育出版社,2000.
[2] 王萌长, 刘铮, 周文群, 等. 结构力学[M].冶金工业出版社,1998.
[3] 《建筑结构静力计算手册》编写组.建筑结构静力计算手册[M].中国建筑工业出版社,2000.
[4] 张宪恩. 在水平力作用下桩的内力分析及应用探讨[J].攀枝花建筑,1998(3).
董兴强(1981~),男,本科,工程师,从事结构设计工作。
TU473.1+3
A
[定稿日期]2016-06-11
