多流形的非监督线性差分投影算法*
2016-11-22杨章静万鸣华王巧丽张凡龙杨国为
杨章静,万鸣华,2,3+,王巧丽,张凡龙,杨国为
1.南京审计大学 工学院,南京 211815
2.南京理工大学 高维信息智能感知与系统教育部重点实验室,南京 210094
3.南京晓庄学院 可信云计算与大数据分析重点实验室,南京 211171
4.南昌航空大学 江西省图像处理与模式识别重点实验室,南昌 330063
多流形的非监督线性差分投影算法*
杨章静1,万鸣华1,2,3+,王巧丽4,张凡龙1,杨国为1
1.南京审计大学 工学院,南京 211815
2.南京理工大学 高维信息智能感知与系统教育部重点实验室,南京 210094
3.南京晓庄学院 可信云计算与大数据分析重点实验室,南京 211171
4.南昌航空大学 江西省图像处理与模式识别重点实验室,南昌 330063
YANG Zhangjing,WAN Minghua,WANG Qiaoli,et al.Multi-manifold unsupervised linear differential projection algorithm.Journal of Frontiers of Computer Science and Technology,2016,10(11):1577-1586.
针对非监督线性差分投影(unsupervised linear differential projection,ULDP)在特征提取过程中存在的不足,提出了基于多流形的非监督线性差分投影(multi-manifold unsupervised linear differential projection,MULDP)算法,并将其应用于人脸识别中。MULDP首先构造出多流形局部近邻图和多流形最大全局方差,然后通过多目标最优化问题求解出嵌入在高维空间的低维流形。这种映射不仅能表示全局结构,还能表示局部结构。该算法可以得到嵌入在高维空间的低维流形,更好地实现了局部与全局结构信息的有效保持。在ORL、Yale及AR人脸库上的实验结果验证了所提算法的优越性。
人脸识别;特征提取;多流形;非监督线性差分投影(ULDP)
1 引言
特征提取是人脸识别处理过程的核心,提取有效人脸特征是人脸识别的关键步骤,人脸特征的有效性直接影响人脸识别的结果[1-2]。对于人脸识别来说,寻找快速、有效的特征提取方法是人脸识别技术取得突破的关键,也是当前研究的热点[3-4]。
目前,关于特征提取技术[5]的研究正如火如荼,方法也有多种,但概括起来主要有两大类型:一类是基于全局特征的特征提取,另一类是基于局部特征的特征提取。全局特征是指其特征向量的每一维都包含了人脸图像所有部分(甚至所有像素)的信息,它反映的是人脸的整体属性。基于全局的特征方法主要包括PCA(principal component analysis)[6]、LDA(linear discriminant analysis)[7]、2DPCA(two-dimensional PCA)[8]等。与全局特征不同的是,局部特征信息的每一维都只对应人脸图像的一个局部区域,侧重于提取人脸的细节特征。基于局部特征的提取方法主要包括LPP(locality preserving projection)[9]、LLE(locally linear embedding)[10]、LBP(local binary pattern)[11-13]等。局部特征对人脸的光照、表情和遮挡等变化不敏感,因此相对于基于全局特征的提取方法,基于局部特征的提取方法具有更好的鲁棒性,在近些年来受到越来越多研究者的关注[14-15]。也有很多研究者提出同时利用全局和局部特征来表示人脸[16-17]。Wan等人在PCA和LLE基础上,同时考虑样本分布全局性和局部性,结合PCA和LLE的特点,提出了非监督线性差分投影(unsupervised linear differential projection,ULDP)[16]的特征提取方法;Yang等人在同时考虑局部散度和非局部散度的基础上,提出了非监督鉴别投影(unsupervised discriminant projection,UDP)[17]的特征提取方法。这些方法在加强数据样本点之间的关联性时,能有效地对局部与全局流形结构进行同时保持,也就是说在高维空间保持近邻的数据点映射到内在低维空间后仍保持近邻,反之,在高维空间不能保持近邻的数据点映射到内在低维空间继续保持其非近邻的关系,因此应该同时对局部与全局流形结构进行保持,进而发现隐藏于高维空间样本点间的流形,以提高人脸识别的精度。但这些方法也存在两个缺陷:一是在学习过程中过分依赖训练样本的数目,当遇到小样本问题时,就严重限制了此方法的应用;二是在提取的众多特征中,无法揭示哪些特征对分类与预测起主导作用。
针对以上问题,本文借鉴ULDP的思想,提出了一种结合多流形的兼顾样本全局结构与局部结构的特征提取算法,即基于多流形的非监督线性差分投影(multi-manifold unsupervised linear differential projection,MULDP)。MULDP首先将一个样本分成的局部小块都构造在同一个流形上,使得每个样本都有属于自己的流形,即位于同一个特征子空间;然后分别给出PCA和LLE的多流形表示,优化目标是最大化各个流形的全局方差,最小化流形内的局部嵌入。MULDP相对于ULDP,不仅解决了小样本问题,而且进一步提高了识别率。在人脸数据库上的实验表明,MULDP较其他算法能获得较好的识别效果。
2 相关知识
2.1 非监督的线性差分投影
基于局部特征的流形学习方法往往只考虑流形上距离相近的数据点,这样就会导致本来距离很远的点映射后反而变成距离相近点的情形,因此应该有效地保持局部流形结构同时又保持全局流形结构,寻找出潜藏在高维数据空间中的低维流形结构,以此来提高算法的识别率。
ULDP是一种非监督的算法,该算法首先用流形距离构建全局方差图和局部近邻图,然后用其表征全局结构和局部结构信息,最后求解在约束条件下的优化问题得到的特征向量,以此来表征嵌入在高维空间中的低维子流形。
ULDP算法不仅保持了局部近邻数据点之间的内在联系,还保证了相距较远的数据点之间的非局部散度达到最大,因此该算法有效地实现了既保持数据的局部结构,又保持全局结构。
2.2 ULDP算法描述


其中,λi是上述特征方程的特征值;ωi是对应的特征向量。为了使目标函数最小,只需求解d个最小特征值对应的特征向量组成投影矩阵W=[ω1,ω2,…,ωd]。
3 多流形非监督线性差分投影
根据以上分析,ULDP算法在特征提取时能保持局部近邻数据点之间的内在联系,使得相距较远的数据点之间的非局部散度达到最大。然而针对人脸识别中训练样本少的情况,ULDP算法的识别率会显著下降,识别因此会变得无能为力。
3.1MULDP算法基本思想
将一幅人脸图像分成t个小块,此时就变成了很多幅小图片xit,一张人脸图像的t张小图像分布在同一个流形上,就构成一个流形Mi=[xi1,xi2,…,xit]。很多个人的流形,那就是多流形(multi-manifold),用M=[M1,M2,…,MN]表示。现在要对一个由很多个小图像块组成的流形Mi=[xi1,xi2,…,xit]进行降维。其中每个图像块xir∈Rd,1≤i≤N,1≤r≤t是d维的,多流形判别分析算法的目标就是寻找一个降维矩阵Wi,i=1,2,…,N,将原始训练样本的维数降为di维,多流形算法简化模型如图1所示。
MULDP算法兼顾样本全局结构与局部结构,结合了多流形,首先将样本的局部嵌入和全局方差用多流形形式表示出来,然后在低维子空间最大化各个流形的全局方差,最小化流形内的局部嵌入。
3.2MULDP算法描述
根据前文所述,可得MULDP算法描述如下。


MULDP算法不仅保持局部近邻数据点之间的内在联系,还保证了相距较远的数据点之间的非局部散度达到最大,实现既保持了数据的局部结构又保持了全局结构。为了避免小样本问题,引入一个平衡参数α(0≤α<1)。

Fig.1 Simplified model of multi-manifold algorithm图1 多流形算法简化模型

其中,λi是上述特征方程的特征值;ωi是对应的特征向量。为了使目标函数最小,取前d个最小特征值对应的特征向量组成投影矩阵W=[ω1,ω2,…,ωd]。
3.3 分类
经过以上特征提取后,每一幅原始图像都得到MULDP的投影矩阵Wi,i=1,2,…,N后,下面就需要对测试样本进行处理,进而完成识别分类的目标,其具体步骤如下。
(1)求测试样本的低维子空间表示
给出一个新的测试样本T,首先将其分成t块不重复并且不叠加的局部小块,随后把这些小块建模为新的流形Mi=[xi1,xi2,…,xit],很多个人的流形,那就是多流形,用M=[M1,M2,…,MN]表示。现在要对一个由很多个小图像块组成的流形Mi=[xi1,xi2,…,xit]进行降维,那么它到任意一个训练样本的距离为d(MT,Mi)。 yi=WiTMi=[yi1,yi2,…,yit]及 yT=WiTMT=[yT1, yT2,…,yTt]分别为流形Mi和MT通过Wi投影后的低维子空间表示。
(2)求测试样本与训练样本之间的距离
对每个yT中的yTj,从yi中找出它的k个近邻Gk(yTj),用Gk(yTj)的加权平均去重组yTj,那么yTj到流形Mi的距离为:

其中,cs为近邻对 yTj的重构系数,。所有的yTj的距离加起来求解平均就是MT到Mi的流形距离,即:
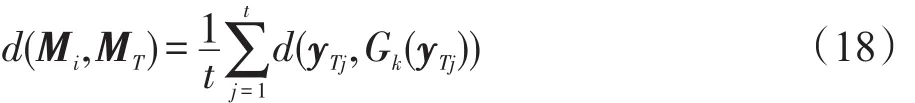
(3)分类
根据求出的N个测试样本与训练样本之间的距离进行对比,找出其中最小的那个距离,这个最小距离如果是测试样本与第i个训练样本之间的距离,那么就可以判定这个测试样本是第i类样本,即:

4 实验及结果分析
为评估所提算法的性能,在ORL、Yale及AR数据库上进行人脸识别实验来验证所提算法的有效性,主要采用识别率作为验证指标。作为对比,同时还采用了其他典型算法如PCA、LDA、LLE、NPE、LPP、ULDP等进行实验。在实验中,由于人脸图像维数较高,在运行以上算法时,首先采用PCA算法对人脸图像进行降维预处理,接着采用各算法进行特征提取,最后采用最近邻分类器进行识别。
4.1 参数α的选取和测试
MULDP算法的目的是求解出嵌入在高维空间的低维子流形,使得投影后不仅保持局部近邻数据点之间的内在联系,还保证相距较远的数据点之间的距离达到最大。为避免出现小样本问题,加入一个平衡参数α(0<α<1),参数α的不同取值会产生不同的分类识别率,尤其当α取值不合适时,计算所得的分类无法正确反映样本的分布信息,从而降低算法的识别性能。因此在原有分类概率计算式中引入参数α,不仅使得计算式更加灵活,而且可以通过调节α使得识别率在某种程度上得到进一步提高。设置α的值从0.1到0.9,间隔为0.1,在ORL、Yale和AR人脸数据库上选取6个训练样本,MULDP的最大平均识别率随α变化的情况如表1所示。
从表1中实验结果可以看出,在ORL、Yale和AR库上,α分别取0.5、0.4和0.6时,MULDP识别率分别为98.57、96.79和97.08,此时识别效果最好。鉴于该实验结果,后续的3个实验中,α分别取0.5、0.4和0.6进行实验。
4.2 ORL人脸库实验
ORL人脸库(http://www.cl.cam.ac.uk/research/dtg/ attarchive/facedatabase.html)包含40个人,其中每个人各拥有10幅分辨率为112×92的图像。ORL库中某人的10幅图像如图2所示。

Table 1 Recognition rates and corresponding dimensions of MULDP with differentαwhen training number is 6 on ORL,Yale andAR databases表1 ORL、Yale和AR库上训练样本数为6时MULDP在α取不同值时的识别率及投影维数

Fig.2 10 images of one person on ORL database图2 ORL库中某人的10幅图像
实验中用于训练的样本是从ORL库中随机抽取的每人3、4、5、6幅图像,其余的作为测试样本。对于每一个不同的训练样本大小的实验,为综合对比,独立运行50次。为便于比较,表2给出了在ORL人脸库上不同算法的最大识别率以及对应的特征维数。不同算法的平均最大识别率随训练样本的变化情况如图3所示。

Fig.3 Recognition rates of MULDP and other algorithms with differentlon ORL database图3 ORL库上MULDP与其他算法在l取不同样本数时的最大识别率对比

Table 2 Optimal recognition rates and corresponding dimensions of MULDP compared with other algorithms on ORL database表2 ORL库上MULDP与其他算法最佳识别率及特征维数比较
4.3 Yale人脸库实验
Yale人脸库(http://cvc.yale.edu/projects/yalefaces/ yalefaces.html)中包括15人,其中每个人各拥有11幅分辨率为100×80的图像。Yale库中某人的11幅图像如图4所示。

Fig.4 11 images of one person on Yale database图4 Yale库中某人的11幅图像
实验中用于训练的样本是从Yale库中随机抽取的每人2、3、4、5、6幅图像,其余的作为测试样本。对于每一个不同的训练样本大小的实验,也独立运行50次。表3给出了在Yale人脸库上不同算法的最大识别率以及对应的特征维数。不同算法的平均最大识别率随训练样本的变化情况如图5所示。

Fig.5 Recognition rates of MULDP and other algorithms with differentlon Yale database图5 Yale库上MULDP与其他算法在l取不同样本数时的最大识别率对比
4.4 AR人脸库实验
AR人脸库(http://rvl1.ecn.purdue.edu/~aleix/aleix_ face_DB.html)中包括120人,其中每个人各拥有不同光照、表情、遮挡的26幅图像,每人前后13幅图像分别拍摄2个时期,时间间隔1个月。图6是AR人脸库中一个子类的20幅图像,两行图像分别拍摄于不同的时期,前后相差两个星期。
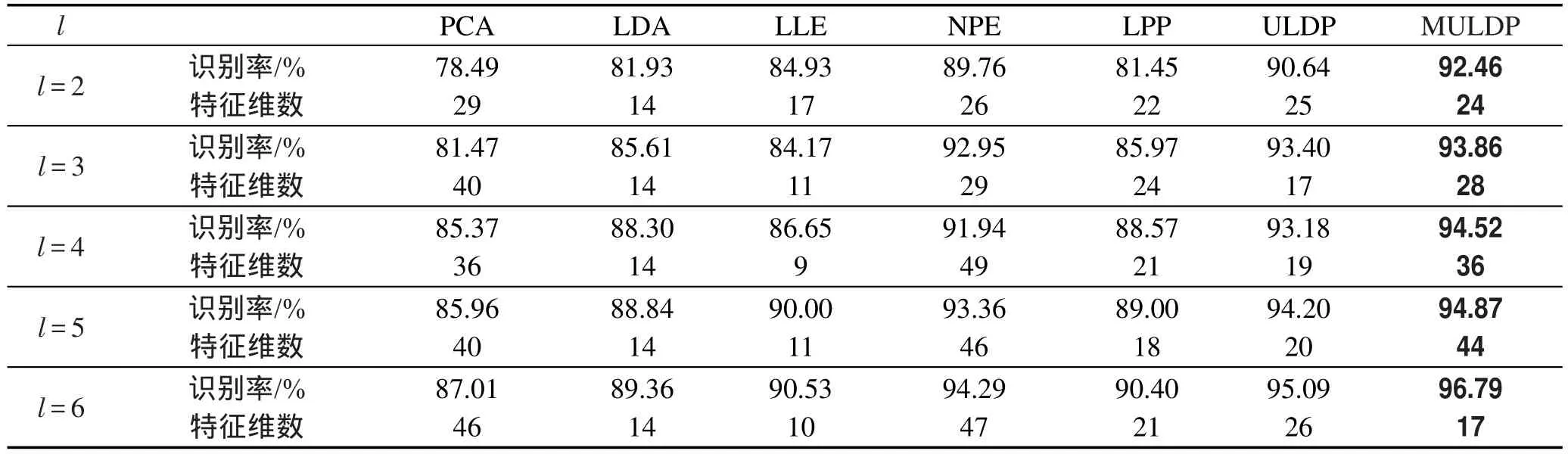
Table 3 Optimal recognition rates and corresponding dimensions of MULDP compared with other algorithms on Yale database表3 Yale库上MULDP与其他算法最佳识别率及特征维数比较

Fig.6 20 images of one person from a subclass onAR database图6 AR人脸库中一个子类的20幅图像
在实验中,选择AR数据库的一个子集,包括前40个人,每个人10幅图像。实验中用于训练的样本是从AR库中随机抽取的每人2、3、4、5、6幅图像,其余的作为测试样本。表4给出了在AR人脸库上不同算法的最大识别率以及对应的特征维数。不同算法的平均最大识别率随训练样本的变化情况示意图如图7所示。

Table 4 Optimal recognition rates and corresponding dimensions of MULDP compared with other algorithms onAR database表4 AR库上MULDP与其他算法最佳识别率及特征维数比较
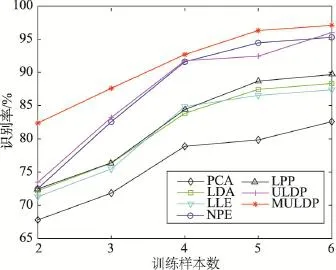
Fig.7 Recognition rates of MULDP and other algorithms with differentlonAR database图7 AR库上MULDP与其他算法在l取不同样本数时的最大识别率对比
4.5 实验结果与分析
根据实验结果,可得结论如下:
(1)表1显示的是ORL、Yale和AR人脸库上,当训练样本为6时,MULDP算法的最大平均识别率随α的变化情况。从表1可以看出,参数α的选择对MULDP算法的识别性能有一定影响,不同的α取值会产生不同的识别率。其中Yale数据库测试样本数最少,参数α为0.4时识别效果最好;AR数据库测试样本数最大,参数α为0.6时识别效果最好。究其原因,主要是由于样本数少时,多流形最小局部散度JL(Wi)要大于多流形最大全局方差JG(Wi),反之多流形最小局部散度JL(Wi)则小于多流形最大全局方差JG(Wi)。
(2)MULDP算法是在ULDP基础上提出的,从表2、表3和表4中的实验数据及结果可以看出,MULDP算法无论在ORL、Yale还是在AR人脸库上,其识别率都比ULDP好,MULDP算法性能均要优于ULDP。这主要是由于MULDP算法将每幅图像分成多幅小图像,这些小图像就构成一个流行,多幅图像就构成了多流行,这就解决了ULDP算法存在的小样本问题。
(3)从图3、图5和图7中可以看出,随着训练样本个数的增加,所有实验算法的识别率均得到了进一步的提升。从整体上看,训练样本数由2增加到6的过程中,本文所提算法MULDP的识别率在所有算法中都是最高的,体现了该算法的鉴别性能优于其他算法。
(4)MULDP算法是在低维子空间最大化各个流形的全局方差,最小化流形内的局部嵌入,此算法结合多流形,并且兼顾样本全局结构与局部结构,从而取得了较好的识别效果。
由上述实验图表可知,相较于其他算法,MULDP算法整体均取得了最好效果,这进一步验证了算法的优越性。
5 结束语
针对ULDP算法在处理人脸识别问题时存在的缺陷,提出了多流形的非监督线性差分投影算法MULDP。MULDP结合了PCA与LLE两种算法的优点,特征提取时同时保留了数据中的全局结构和局部结构,可以更好地提取人脸图像数据间的鉴别信息,以此来提高算法的分类性能,使得本文算法更加鲁棒。通过在ORL、Yale和AR人脸库上的实验验证了本文算法的有效性及优越性。
从实验结果可知,α的取值与MULDP算法的识别效果有一定联系,目前如何选择参数仍然是一个难题。因此在后续工作中,如何对α进行取值,使得算法具有稳定的性能并达到最优识别效果是今后需要重点研究的问题。
[1]Ma Xiaohu,Tan Yanqi.Face recognition based on discriminant sparsity preserving embedding[J].Acta Automatica Sinica,2014,40(1):73-82.
[2]Wan Minghua,Li Ming,Yang Guowei,et al.Feature extraction using two-dimensional maximum embedding difference [J].Information Sciences,2014,274:55-69.
[3]Nixon M,Aguado A S.Feature extraction and image processing[M].2nd ed.Orlando,USA:Academic Press,2008.
[4]Yang Xiaomin,Wu Wei,Qing Linbo,et al.Image feature extraction and matching technology[J].Optics and Precision Engineering,2009,17(9):2276-2282.
[5]Bartlett M S,Lades H M,Sejnowski T J.Face recognition by independent component analysis[J].IEEE Transactions on Neural Networks,2002,13(6):1450-1464.
[6]Turk M,Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.
[7]Yu Hua,Yang Jie.A direct LDA algorithm for high-dimensional data-with application to face recognition[J].Pattern Recognition,2001,34(10):2067-2070.
[8]Yang Jian,Zhang D,Frangi A F,et al.Two-dimensional PCA: a new approach to appearance-based face representation and recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(1):131-137.
[9]He Xiaofei,Yan Shuicheng,Hu Yuxiao,et al.Face recognition using Laplacianfaces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3):328-340.
[10]Roweis S T,Saul L K.Nonlinear dimensional reduction by locally linear embedding[J].Science,2000,290(550):2323-2326.
[11]Ahonen T,HadidA,Pietikainen M.Face description with local binary patterns:application to face recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006,28(12):2037-2041.
[12]Zhang Baochang,Gao Yongsheng,Zhao Sanqiang,et al.Local derivative pattern versus local binary pattern:face recognition with high-order local pattern descriptor[J].IEEE Transactions on Image Processing,2010,19(2):533-544.
[13]Wolf L,Hassner T,Taigman Y.Effective unconstrained face recognition by combining multiple descriptors and learned background statistics[J].IEEE Transactions on PatternAnalysis and Machine Intelligence,2011,33(10):1978-1990.
[14]Lai Zhihui,Xu Yong,Chen Qingcai,et al.Multilinear sparse principal component analysis[J].IEEE Transactions on Neural Networks and Learning Systems,2014,25(10):1942-1950.
[15]Lai Zhihui,Xu Yong,Jin Zhong,et al.Human gait recognition via sparse discriminant projection learning[J].IEEE Transactions on Circuits and Systems for Video Technology, 2014,24(10):1651-1662.
[16]Wan Minghua,Lai Zhihui,Jin Zhong.Locally minimizing embedding and globally maximizing variance:unsupervised linear difference projection for dimensionality reduction[J].Neural Processing Letters,2011,33(3):267-282.
[17]Yang Jian,Zhang D,Yang Jingyu,et al.Globally maximizing, locally minimizing:unsupervised discriminant projection with applications to face and palm biometrics[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007,29(4):650-664.
附中文参考文献:
[1]马小虎,谭延琪.基于鉴别稀疏保持嵌入的人脸识别算法[J].自动化学报,2014,40(1):73-82.

YANG Zhangjing was born in 1979.He is a lecturer at School of Technology,Nanjing Audit University.His research interests include computer vision and pattern recognition,etc.
杨章静(1979—),男,江苏南京人,南京审计大学工学院讲师,主要研究领域为计算机视觉,模式识别等。

WAN Minghua was born in 1978.He is an associate professor at School of Technology,Nanjing Audit University. His research interests include pattern recognition and intelligent computation,etc.
万鸣华(1978—),男,江西南昌人,南京审计大学工学院副教授,主要研究领域为模式识别,智能计算等。

WANG Qiaoli was born in 1990.She is an M.S.candidate at School of Information Engineering,Nanchang Hangkong University.Her research interests include artificial intelligence and intelligent computation,etc.
王巧丽(1990—),女,山东菏泽人,南昌航空大学信息工程学院硕士研究生,主要研究领域为人工智能,智能计算等。

ZHANG Fanlong was born in 1985.He is a lecturer at School of Technology,Nanjing Audit University.His research interests include computer vision and pattern recognition,etc.
张凡龙(1985—),男,山东泰安人,南京审计大学工学院讲师,主要研究领域为计算机视觉,模式识别等。

YANG Guowei was born in 1964.He is a professor at School of Technology,Nanjing Audit University.His research interests include pattern recognition and artificial intelligence,etc.
杨国为(1964—),男,江西南昌人,南京审计大学工学院教授,主要研究领域为模式识别,人工智能等。
Multi-Manifold Unsupervised Linear Differential ProjectionAlgorithmƽ
YANG Zhangjing1,WAN Minghua1,2,3+,WANG Qiaoli4,ZHANG Fanlong1,YANG Guowei1
1.School of Technology,NanjingAudit University,Nanjing 211815,China
2.Key Laboratory of Intelligent Perception and Systems for High-Dimensional Information of Ministry of Education,Nanjing University of Science and Technology,Nanjing 210094,China
3.Key Laboratory of Trusted Cloud Computing and Big Data Analysis,Nanjing Xiaozhuang University,Nanjing 211171,China
4.Key Laboratory of Jiangxi Province for Image Processing and Pattern Recognition,Nanchang Hangkong University,Nanchang 330063,China
+Corresponding author:E-mail:wmh36@nau.edu.cn
To overcome the drawbacks of existing unsupervised linear differential projection(ULDP),this paper proposes a novel algorithm called multi-manifold unsupervised linear differential projection(MULDP)for face recogni-tion.Firstly,multi-manifold local neighborhood graph and the largest global variance are constructed.Nextly,a lowdimensional manifold embedded in high-dimensional space is calculated through the multi-objective optimization.This mapping can represent not only the global structure but also the local structure.MULDP can get the low-dimensional manifolds embedded in a high-dimensional space and maintain the local and global structural information effectively. The experimental results on the ORL,Yale andAR face databases demonstrate the superiority of the proposed algorithm.
face recognition;feature extraction;multi-manifold;unsupervised linear differential projection(ULDP)
10.3778/j.issn.1673-9418.1604045
A
TP391.4
*The Natural Science Foundation of Jiangsu Higher Education Institutions under Grant Nos.15KJB520018,12KJA63001(江苏省属高校自然科学基金);the National Natural Science Foundation of China under Grant Nos.61503195,61462064,61203243,61272077 (国家自然科学基金);the Key Laboratory of Intelligent Perception and Systems for High-Dimensional Information of Ministry of Education(Nanjing University of Science and Technology)under Grant No.30920140122006(高维信息智能感知与系统教育部重点实验室(南京理工大学)基金).
Received 2016-04,Accepted 2016-06.
CNKI网络优先出版:2016-06-02,http://www.cnki.net/kcms/detail/11.5602.TP.20160602.1144.012.html
