自动确定聚类中心的密度峰聚类*
2016-11-22葛洪伟苏树智
李 涛,葛洪伟,2+,苏树智
1.江南大学 物联网工程学院,江苏 无锡 214122
2.轻工过程先进控制教育部重点实验室(江南大学),江苏 无锡 214122
自动确定聚类中心的密度峰聚类*
李 涛1,葛洪伟1,2+,苏树智1
1.江南大学 物联网工程学院,江苏 无锡 214122
2.轻工过程先进控制教育部重点实验室(江南大学),江苏 无锡 214122
LI Tao,GE Hongwei,SU Shuzhi.Density peaks clustering by automatic determination of cluster centers. Journal of Frontiers of Computer Science and Technology,2016,10(11):1614-1622.
密度峰聚类是一种新的基于密度的聚类算法,该算法不需要预先指定聚类数目,能够发现非球形簇。针对密度峰聚类算法需要人工确定聚类中心的缺陷,提出了一种自动确定聚类中心的密度峰聚类算法。首先,计算每个数据点的局部密度和该点到具有更高密度数据点的最短距离;其次,根据排序图自动确定聚类中心;最后,将剩下的每个数据点分配到比其密度更高且距其最近的数据点所属的类别,并根据边界密度识别噪声点,得到聚类结果。将新算法与原密度峰算法进行对比,在人工数据集和UCI数据集上的实验表明,新算法不仅能够自动确定聚类中心,而且具有更高的准确率。
聚类;密度峰;自动聚类;密度聚类
1 引言
聚类是按照某个特定标准,根据数据自身的信息相似度,把没有给定划分类的数据集分割成不同的类或簇,使不同簇间的数据对象具有最小相似性,同一簇内的数据对象具有最大相似性[1]。聚类作为一种无监督的数据分析方法,在数据挖掘、模式识别、机器学习、信息检索等领域[2]已经得到了广泛研究和应用。
目前,已经有许多聚类算法被提出。比较典型的有:基于划分的K-means[3]、K-medoids[4]等聚类;基于层次的CURE(clustering using representatives)[5]、Chameleon[6]等聚类;基于网格的STING(statistical information grid)[7]、WaveCluster[8]等聚类;基于模型的统计学聚类和神经网络聚类;基于图论的谱聚类[9-10]以及基于密度的DBSCAN(density-based spatial clustering of applications with noise)[11]、OPTICS(ordering points to identify the clustering structure)[12]等聚类。
2014年,Rodriguez等人在《Science》上提出了一种新的基于密度的密度峰聚类(density peaks clustering,DPC)算法[13]。DPC算法主要分两步:首先,通过“决策图”人工选取密度峰,也即聚类中心;其次,分配剩余数据点,得到聚类结果。
DPC算法虽然简单高效,但却无法自动确定聚类中心。特别是针对一些特殊数据集,通过决策图人工选取聚类中心时容易出错。针对DPC算法这一缺陷,本文提出了一种自动确定聚类中心的密度峰聚类算法(automatically density peaks clustering,ADPC)。ADPC算法能够根据排序图自动确定聚类中心,具有更优的聚类结果和更高的准确率。
2 密度峰聚类及其缺陷
密度峰聚类[13]算法只有一个输入参数,不需要预先指定聚类数目,能够发现非球形的簇。算法基于数据点之间的距离测度,不需考虑概率分布或多维密度函数,性能不受数据空间维度影响,可以处理高维数据。
算法将具有如下特点的数据点视为聚类中心:该点被具有相对较低局部密度的邻居点包围,且与其他具有更高密度的数据点之间具有相对较大的距离。对于每个数据点 j,只需计算两个变量,即点 j的局部密度ρj和该点到具有更高局部密度的点的最短距离δj。数据点j的局部密度ρj计算方式为:

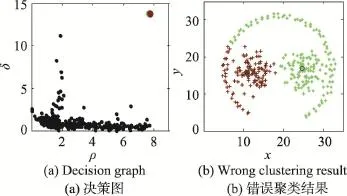
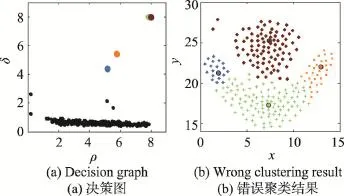
其中,djk是数据点之间的距离;dc是截断距离。设数据点的邻居点总数占数据集样本点总数N的比例值为P∈(0,100),将M=N(N-1)/2个距离dmn(m δj为数据点 j到具有更高局部密度的点k的最短距离,其计算方式为: 对于具有全局最高密度的数据点,令 δj= maxk(djk)。通常的,具有局部或全局最大密度的数据点的δj比其最近邻距离要大。算法将同时具有相对较大ρ和δ的数据点视为聚类中心。 聚类中心找到后,下一步将剩下的每个数据点分配到比其密度更高且距其最近的数据点所属的簇。不像K-means等算法[2,14]需要对目标函数进行多次迭代优化,数据点分配只需上述一步即可完成。为了识别噪声点,DPC算法为每个簇定义边界区域密度:属于这个簇并且与其他簇的数据点之间的距离小于dc的数据点总数。局部密度ρ高于边界区域密度的点被视为簇的核心点,否则被视为噪声点。 DPC算法虽然简单高效,但却需要通过决策图人工选取聚类中心。这种方法对每个簇内都有唯一密度峰或者簇数很少的数据集比较有效,因为此时从决策图中比较容易判断出具有相对较大ρ和δ的数据点。但针对以下情况,决策图则表现出明显的局限性: (1)如图1所示,在决策图上,除了明显的密度峰点,一些具有相对较大ρ和较小δ,或者相对较小ρ和较大δ的数据点也可能是聚类中心,但这些点很容易被人为地忽略,使得少选了聚类中心,最终导致属于不同簇的一些数据点被错误地合并为同一个簇。 (2)如图2所示,如果同一簇内出现了多个密度峰,则这些点很容易被错选为多余的聚类中心,导致同一个簇被错误地分割为多个子簇。 (3)在处理具有较多聚类中心的数据集时,同样比较容易出现上述错选聚类中心的情况。 可见,DPC算法对聚类中心的选择比较敏感,容易出现人为地少选、多选聚类中心的问题。这种缺陷在处理一些特殊数据集时表现得更为突出。 Fig.1 DPC gets less cluster centers by decision graph图1 DPC算法通过决策图少选聚类中心 Fig.2 DPC gets redundant cluster centers by decision graph图2 DPC算法通过决策图多选聚类中心 3.1 自动确定聚类中心 定义1γj为衡量点j是否为聚类中心的指标: 显然,当点 j为聚类中心时,ρj或δj具有较大值,则γj也具有较大值,因而γj较大的点很可能是聚类中心。对γ进行降序排列,记排序后的点编号为i,绘制γ关于点i的前个点的函数图,称之为“γ排序图”。 其中, P=8时,图2(b)中数据集的决策图与γ排序图如图3所示。从图3中可以看出,聚类中心都位于拐点之前。整体而言,大多数数据点的γ值较小且彼此接近,只有拐点之前的少数数据点γ值较大且彼此差异也较大,将这少数点称为潜在聚类中心。 定义3潜在聚类中心定义为: Fig.3 Decision graph andγsorting graph for data in Fig.2(b)whenP=8(top-30 points 2 clusters)图3 P=8时图2(b)数据集的决策图与γ排序图(前30个点2个簇) 准确确定拐点是算法的关键。根据定义2,拐点为γi值前后差值大于阈值θ的所有点中γ值最小的点,因而一种有效查找拐点的方法为:从右往左依次判断γ排序图中的点,查找第一个满足定义2中条件的点,该点即为拐点。这种方法确定的拐点能够保证拐点之前具有尽可能多的潜在聚类中心,从而防止后续处理时漏选任何一个可能的实际聚类中心。 显然,潜在聚类中心的个数一般多于实际聚类中心的个数。如果把所有潜在聚类中心都当作实际聚类中心进行聚类,则某些簇中可能会被指定多余的聚类中心,导致同一个簇被错误地分割为多个子簇。在DPC算法中,实际聚类中心通常都位于数据点分布相对比较稠密的区域,而且彼此之间都具有相对较大的距离。因而在一个具有高密度区域的簇中,若存在多个潜在聚类中心(密度峰点),则这些潜在聚类中心彼此之间通常会比较接近。把查找到的属于某个簇的第一个潜在聚类中心当作该簇的唯一实际聚类中心;如果其他某个潜在聚类中心与该簇中已知实际聚类中心的最短距离小于dc,则将该潜在聚类中心视为被错选的多余的聚类中心,并将其当作簇成员处理,否则将该潜在聚类中心当作另一个簇的实际聚类中心。最终,实现从潜在聚类中心中准确“筛选”出实际聚类中心的目的。 3.2 ADPC算法步骤描述 综上所述,首先利用γ排序图确定拐点及潜在聚类中心,然后从潜在聚类中心中自动确定实际聚类中心,最后分配剩余数据点,得到聚类结果。算法主要步骤描述如下。 输入:实验数据集X={x1,x2,…,xn},数据点的邻居点总数占数据集样本总数的比例值P。 输出:聚类结果C={C1,C2,…,Ck},k为类数。 (1)根据P计算dc,计算每个数据点i的局部密度ρi和该点到具有更高局部密度数据点的最短距离δi。 (2)计算γi=ρiδi,将γ降序排列,绘制γ排序图。根据γ排序图自动查找拐点ap,找到潜在聚类中心。 (3)默认具有最大γ值的第一个点为一个实际聚类中心。从已经被确定为实际聚类中心的所有点中,找到距离点i最近的点 j,计算距离Dist(i,j),记MinDist=Dist(i,j)。如果MinDist>dc,则点i被确定为一个新的实际聚类中心,否则点i被视为点j所属的簇的成员。其中,i=2,3,…,ap,j=1,2,…,i-1。 (4)重复步骤(3),直到i=ap,自动确定聚类中心的过程结束。 (5)将剩下的每个数据点分配到具有更大ρ的最近邻点所属的簇,计算边界区域密度,根据边界区域密度识别噪声点。 使用DS7数据集自动确定聚类中心的过程对算法原理做进一步解释。P=3.5(dc=2.52)时DS7数据集的实验结果如图4所示。图4(a)中为拐点之前(包括拐点)的9个潜在聚类中心按γ值从大到小进行了编号;图4(b)为图4(a)中9个潜在聚类中心的实际位置分布及错误聚类结果;图4(c)标示出了算法最后自动确定的7个实际聚类中心;图4(d)为图4(c)对应的理想聚类结果。首先根据定义2,将γ值前后整体差异比较大的点9选作拐点,将点1至点9选作潜在聚类中心;然后依次判断9个点能否作为实际聚类中心。默认具有最大γ值的点1为一个实际聚类中心,点2找到已经被确定为实际聚类中心且距其最近的点1,计算点1与点2之间的距离 Dist(1,2)= 21.68,因为Dist(1,2)>dc,所以点2被确定为一个新的实际聚类中心;相似的,点3、4、5、6、7依次被确定为实际聚类中心;点8从已被确定为实际聚类中心的点中找到距其最近的点1,但Dist(1,8) Fig.4 Procedure of determining cluster centers on DS7 byADPC图4 ADPC算法在DS7数据集上自动确定聚类中心的过程 Fig.5 Decision graph and ideal clustering result of DS15 by DPC whenP=2(15 clusters)图5 P=2时DPC算法在DS15数据集上的决策图与理想聚类结果(15个类) 3.3 ADPC算法时间复杂度分析 设实验数据集样本总数为n,根据3.2节的描述,算法第(1)步根据P计算dc时,首先计算欧式距离矩阵的时间复杂度为O(n2),对欧式距离矩阵上三角n(n-1)/2个距离进行快速排序的时间复杂度为O(n2lbn),计算 ρ和δ的时间复杂度为O(n2);第(2)步中计算γ及自动查找拐点的时间复杂度为O(n),采用快速排序对γ降序排列的时间复杂度为O(n2lbn);第(3)、(4)步中自动确定聚类中心的时间复杂度综合为O(n2);第(5)步中分配数据点的时间复杂度为O(n),识别噪声点的时间复杂度为O(n2)。综上所述,ADPC算法的时间复杂度为O(n2lbn)。 为了验证ADPC算法的性能,分别在人工数据集和UCI数据集上进行了实验。 4.1 人工数据集 实验中用到的人工数据集有两个,数据集的相关信息见表1。使用表1中数据集,分别运行DPC与ADPC算法,实验结果如图5~图12所示。 Table 1 Synthetic data sets表1 人工数据集 Fig.6 γsorting graph and ideal clustering result of DS15 byADPC whenP=2(15 clusters)图6 P=2时ADPC算法在DS15数据集上的γ排序图与理想聚类结果(15个类) Fig.7 Decision graph and wrong clustering result of DS15 by DPC whenP=3.5(11 clusters)图7 P=3.5时DPC算法在DS15数据集上的决策图与错误聚类结果(11个类) Fig.8 γsorting graph and ideal clustering result of DS15 byADPC whenP=3.5(15 clusters)图8 P=3.5时ADPC算法在DS15数据集上的γ排序图与理想聚类结果(15个类) Fig.9 Decision graph and ideal clustering result of DS31 by DPC whenP=2(31 clusters)图9 P=2时DPC算法在DS31数据集上的决策图与理想聚类结果(31个类) Fig.10 γsorting graph and ideal clustering result of DS31 byADPC whenP=2(31 clusters)图10 P=2时ADPC算法在DS31数据集上的γ排序图与理想聚类结果(31个类) Fig.11 Decision graph and wrong clustering result of DS31 by DPC whenP=2.4(23 clusters)图11 P=2.4时DPC算法在DS31数据集上的决策图与错误聚类结果(23个类) Fig.12 γsorting graph and ideal clustering result of DS31 byADPC whenP=2.4(31 clusters)图12 P=2.4时ADPC算法在DS31数据集上的γ排序图与理想聚类结果(31个类) 针对DS15数据集,P∈[1.1,3.3]时,两种算法虽然都能得到理想聚类结果,但DPC算法选取聚类中心时具有很大的不确定性;P∈[3.4,3.7]时,DPC算法已经无法选取出准确的聚类中心,而ADPC算法依然可以自动确定全部15个聚类中心并得到理想聚类结果。其中P=2,P=3.5时,两种算法在DS15数据集上的聚类结果分别如图5~图8所示。图5表明,DPC算法虽然最终能够得到15个类,但在图5(a)中,因人工选择具有主观性,很可能会将聚类中心错选为2个、3个等;而在图6、图8中,ADPC算法不存在错选聚类中心的情况。相似的,针对DS31数据集,P∈[1.1,2.1]时,ADPC算法比DPC算法能够更易且自动得到理想聚类结果;而P∈[2.2,2.4]时,DPC算法经过多次尝试,最多也只能得到错误的30个类,但ADPC算法依然可以自动确定全部31个聚类中心并得到理想的聚类结果。其中P=2,P=2.4时,两种算法在DS31数据集上的聚类结果分别如图9~图12所示。上述实验表明,ADPC算法避免了DPC算法通过决策图人工选取聚类中心时出错的可能性,特别是当DPC算法无法选取全部聚类中心时,ADPC算法不仅能够基于γ排序图自动准确地确定聚类中心,而且具有更优的聚类结果。 4.2 UCI数据集 为了进一步验证ADPC算法性能,使用表2中4个常用UCI数据集进行实验。实验采用F-measure[15]与NMI(normalized mutual information)[16]指标评价聚类结果。 Table 2 UCI data sets表2 UCI数据集 在最佳P值下,DPC算法与ADPC算法在表2中数据集上聚类所得F-measure与NMI指标值见表3。表3表明,除了在处理Seeds数据集时两种算法具有相同的F-measure与NMI值,在其他3个数据集上,ADPC算法得到的两个指标值均比DPC算法更优。整体而言,ADPC算法能够得到更优的聚类结果,具有更高的准确度。 Table 3 Comparison of F-measure and NMI表3 两种算法的F-measure与NMI指标值对比 4.3 算法运行效率分析对比 根据3.3节描述,ADPC算法的时间复杂度为O(n2lbn)。根据文献[13],DPC算法的时间复杂度为O(n2lbn)。可见,ADPC算法虽然增加了自动确定聚类中心的能力,但时间复杂度仍与DPC算法在同一个数量级。表4为两种算法在表1、表2中6个数据集上的运行时间对比,表中时间为算法在同一数据集上运行10次所用的平均时间,DPC算法忽略在决策图上人工选取聚类中心环节所用时间。两种算法均在Matlab R2013a上编程实现,在同一PC机(Windows10 64位操作系统,Intel Core i7 2.5 GHz CPU,4 GB内存)上运行,时间单位为秒。 Table 4 Comparison of running time on different data sets表4 两种算法在不同数据集上的运行时间对比 s 在表4中,ADPC算法只比DPC算法的运行时间多了约0.1 s,差值在0.067 3~0.102 3之间。整体而言,ADPC算法没有显著增加运行时间,这也验证了两种算法具有相同时间复杂度的结论。 针对密度峰聚类(DPC)算法人工难以准确选取聚类中心的缺陷,提出了一种自动确定聚类中心的密度峰聚类算法(ADPC)。与DPC算法相比,ADPC算法在人工数据集上具有更优的结果,在UCI真实数据集上具有更高的准确度。由于ADPC算法主要是在选取聚类中心环节对DPC算法进行了改进,并没有改变DPC算法的数据点分配机制,因而ADPC算法不仅增加了自动确定聚类中心的能力,而且保留了DPC算法的一些优势:即同样只需一个输入参数,不需要预先指定聚类数目,可以识别非球形簇,并且没有增加时间复杂度。 然而,ADPC算法在面对一些簇内没有密度峰或同时具有多个密度峰的复杂流形结构数据集时,会出现能够自动确定聚类中心却无法得到理想聚类结果的问题。这是因为对于流形结构中的某个点a而言,密度更高且距其最近的点b很可能在另一个簇中,这就导致点a被错误地分配到点b所属的簇,最终导致实际属于不同簇的一些点被错误地合并为同一簇。针对这一问题,首先可以考虑使用能够更好地反映数据分布结构特点、簇内与簇间蕴含结构信息的新的距离测度,代替仅能反映聚类结构局部一致性却无法很好地反映全局一致性的欧氏距离;其次,改进算法的分配机制,使得算法能够沿着流形结构寻找密度更高的近邻点,从而使得数据点分配更佳合理。总之,如何使得ADPC算法能够有效处理复杂流形结构数据集,将是下一步的研究内容。 [1]Xu Rui,Wunsch D.Survey of clustering algorithms[J].IEEE Transactions on Neural Networks,2005,16(3):645-678. [2]Aggarwal C C,Reddy C K.Data clustering:algorithms and applications[M].Boca Raton,USA:CRC Press,2013. [3]Jain A K.Data clustering:50 years beyond K-means[J].Pattern Recognition Letters,2010,31(8):651-666. [4]Park H S,Jun C H.Asimple and fast algorithm for K-medoids clustering[J].Expert Systems with Applications,2009,36 (2):3336-3341. [5]Zhou Yajian,Xu Chen,Li Jiguo.Unsupervised anomaly detection method based on improved CURE clustering algorithm[J].Journal on Communications,2010,31(7):18-23. [6]Karypis G,Han E H,Kumar V.Chameleon:hierarchical clustering using dynamic modeling[J].Computer,1999,32 (8):68-75. [7]Ansari S,Chetlur S,Prabhu S,et al.An overview of clustering analysis techniques used in data mining[J].International Journal of Emerging Technology and Advanced Engineering, 2013,3(12):284-286. [8]Amini A,Wah T Y,Saybani M R,et al.A study of densitygrid based clustering algorithms on data streams[C]//Proceedings of the 2011 8th International Conference on Fuzzy Systems and Knowledge Discovery,Shanghai,Jul 26-28, 2011.Piscataway,USA:IEEE,2011,3:1652-1656. [9]Yang Peng,Zhu Qingsheng,Huang Biao.Spectral clustering with density sensitive similarity function[J].Knowledge-Based Systems,2011,24(5):621-628. [10]Guang Junye,Liu Mingxia,Zhang Daoqiang.Spectral clustering algorithm based on effective distance[J].Journal of Frontiers of Computer Science and Technology,2014,8 (11):1365-1372. [11]Yang Jing,Gao Jiawei,Liang Jiye,et al.An improved DBSCAN clustering algorithm based on data field[J].Journal of Frontiers of Computer Science and Technology,2012,6 (10):903-911. [12]Kalita H K,Bhattacharyya D K,Kar A.A new algorithm for ordering of points to identify clustering structure based on perimeter of triangle:OPTICS(BOPT)[C]//Proceedings of the 2007 International Conference on Advanced Computing and Communications,Guwahati,India,Dec 18-21,2007.Piscataway,USA:IEEE,2007:523-528. [13]Rodriguez A,Laio A.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496. [14]McLachlan G,Krishnan T.The EM algorithm and extensions[M].Hoboken,USA:John Wiley&Sons,2007. [15]Yang Yan,Jin Fan,Mohamed K.Survey of clustering validity evaluation[J].Application Research of Computers,2008,25 (6):1630-1632. [16]Cai Deng,He Xiaofei,Han Jiawei.Document clustering using locality preserving indexing[J].IEEE Transactions on Knowledge &Data Engineering,2005,17(12):1624-1637. 附中文参考文献: [5]周亚建,徐晨,李继国.基于改进CURE聚类算法的无监督异常检测方法[J].通信学报,2010,31(7):18-23. [10]光俊叶,刘明霞,张道强.基于有效距离的谱聚类算法[J].计算机科学与探索,2014,8(11):1365-1372. [11]杨静,高嘉伟,梁吉业,等.基于数据场的改进DBSCAN聚类算法[J].计算机科学与探索,2012,6(10):903-911. [15]杨燕,靳蕃,Mohamed K.聚类有效性评价综述[J].计算机应用研究,2008,25(6):1630-1632. LI Tao was born in 1991.He is an M.S.candidate at Jiangnan University,and the member of CCF.His research interests include artificial intelligence and data mining. 李涛(1991—),男,河南商丘人,江南大学硕士研究生,CCF学生会员,主要研究领域为人工智能,数据挖掘。 GE Hongwei was born in 1967.He received the M.S.degree in computer science from Nanjing University of Aeronautics and Astronautics in 1992,and the Ph.D.degree in control engineering from Jiangnan University in 2008. Now he is a professor and Ph.D.supervisor at School of Internet of Things Engineering,Jiangnan University.His research interests include artificial intelligence,machine learning,pattern recognition and their applications. 葛洪伟(1967—),男,江苏无锡人,1992年于南京航空航天大学计算机系获得硕士学位,2008年于江南大学信息学院获得博士学位,现为江南大学物联网工程学院教授、博士生导师,主要研究领域为人工智能,模式识别,机器学习,图像处理与分析。在国际权威期刊、国际会议和国内核心期刊上发表论文70多篇,主持和承担了国家自然科学基金等国家级项目和省部级项目近20项,获省部级科技进步奖多项。 SU Shuzhi was born in 1987.He is a Ph.D.candidate at Jiangnan University.His research interests include pattern recognition and machine learning. 苏树智(1987—),男,山东泰安人,江南大学博士研究生,主要研究领域为模式识别,机器学习。 Density Peaks Clustering byAutomatic Determination of Cluster Centersƽ LI Tao1,GE Hongwei1,2+,SU Shuzhi1 Density peaks clustering is a new density-based clustering algorithm.It can find nonspherical clusters without specifying the cluster number.Aiming at the defect that the density peaks clustering algorithm can only manually determine cluster centers,this paper proposes a density peaks clustering by automatic determination of cluster centers. Firstly,for each data point,two quantities are calculated:the local density and the distance from points of higher density. Then the algorithm automatically searches the clustering centers according to the sorting graph.Finally,each remaining data point is assigned to the same cluster as its nearest neighbor of higher density,and then the noises are recognized according to the border density.Comparing the new algorithm with the density peaks clustering algorithm,the experimental results on synthetic data sets and UCI data sets show that the new algorithm can not only automatically determine cluster centers,but also get better results with higher accuracy. clustering;density peaks;automatically clustering;density clustering 10.3778/j.issn.1673-9418.1510049 A TP181 *The National Natural Science Foundation of China under Grant No.61402203(国家自然科学基金);the Research Innovation Program for College Graduates of Jiangsu Province under Grant No.KYLX15_1169(江苏省普通高校研究生科研创新计划项目). Received 2015-10,Accepted 2016-03. CNKI网络优先出版:2016-03-07,http://www.cnki.net/kcms/detail/11.5602.TP.20160307.1710.004.html
3 自动确定聚类中心的密度峰聚类算法


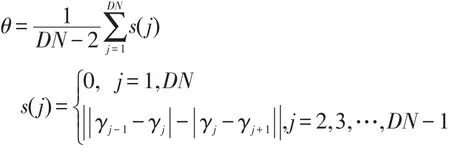
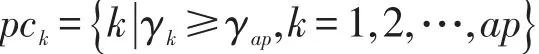



4 实验与分析










5 结束语



1.School of Internet of Things Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China
2.Ministry of Education Key Laboratory of Advanced Process Control for Light Industry(Jiangnan University), Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:ghw8601@163.com
