基于网络基的粗糙复杂网络决策方法及应用*

曹黎侠，黄光球，李 艳

1.西安建筑科技大学 管理学院，西安 710055

2.西安工业大学 理学院，西安 710032

基于网络基的粗糙复杂网络决策方法及应用*

曹黎侠1,2+，黄光球1，李 艳1

1.西安建筑科技大学 管理学院，西安 710055

2.西安工业大学 理学院，西安 710032

CAO Lixia,HUANG Guangqiu,LI Yan.Decision methods and applications of rough complex networks based on network-based.Journal of Frontiers of Computer Science and Technology,2016,10(11):1601-1613.

在一些实际的复杂网络中，网络的管理者为了自身利益最大化和风险最小化，需要做出一些决策，但是现有的研究也只是针对某一实际复杂网络所做的决策，缺乏通用性，也忽略了复杂网络中大量的不确定现象，因此难以取得比较好的决策效果。定义了粗糙复杂网络的网络基，并对网络基的性质进行了研究，证明了网络基与复杂网络等价的结论；提出了两种节点重要性的决策方法和基于网络基的粗糙复杂网络决策方法。最后将基于网络基的粗糙复杂网络决策方法应用于第三方支付粗糙复杂网络的风险分析，建立了二层风险决策模型，给出了量化的决策分析结果。基于网络基的粗糙复杂网络决策方法在第三方支付粗糙复杂网络风险决策模型中的成功应用，说明了该方法的有效性和可行性。

粗糙复杂网络；网络基；决策方法；第三方支付风险分析

1 引言

随着计算机网络的深入研究，科学界发现大量的真实网络具有与规则网络和随机网络都不相同的特征，并将这种处于无规律状态的网络称为“复杂网络（complex networks）”[1-2]。目前国内外关于复杂网络的研究主要集中在以下几个方面[3-4]：（1）网络的结构、性质及演化模型；（2）网络的物理传输过程；（3）利用网络结构控制和优化系统功能。我国学者过去十余年在复杂网络科学的基础研究方面也取得了不少重要的成果，包括复杂网络建模、同步、控制、博弈、传播、节点重要性指标、传播动力学和鲁棒性分析等，但是所有这些研究都没有与复杂网络上的决策方法相关的成果。在一些实际网络中，特别是社会网络和信息网络，网络活动的参与者往往需要做出各种决策，此时他们通常会根据经验进行主观性的决策。这种根据主观臆断所做的决策，缺乏科学性而且风险很大。因此，复杂网络上的决策方法的研究有着重要的理论价值和实际意义。同时在实际复杂网络中，往往存在着太多的不确定现象、不完全信息、大量的冗余数据甚至是错误数据，这些是复杂网络至今还未形成一个通用的决策方法的原因之一。文献[5]对第三方物流企业管理信息系统中配送决策方法进行了分析和建模，文献[6-10]对复杂网络某领域中的一些具体问题进行了决策优化，但这些研究并没有考虑到实际复杂网络上不确定性问题，因此他们的研究有着很大的应用局限性。

粗糙集理论[11]是一种刻画不完全信息和不确定性的数学工具，该理论的主要思想是利用已知的知识库，将不精确或不确定的知识用已知知识库中的知识来近似刻画，并且无需提供问题所需处理的数据集合之外的任何先验信息，因此对问题的不确定性的描述或处理可以说是比较客观的。目前，文献[12]虽然给出了将粗糙集理论应用于决策分析的一种方法，却没有运用粗糙集理论来解决复杂网络上的决策。因此，本文通过对粗糙复杂网络（rough complex networks，RCN）[13]的网络基的定义，完成粗糙复杂网络上决策方法的研究，并用于求解第三方支付粗糙复杂网络上的风险决策问题。

2 网络基的概念及性质

3 复杂网络决策问题的描述与决策方法

在信息网络和社会网络中，网络的效益、安全与风险是人们非常关注的热点问题，这些问题的研究主要包含以下三方面的内容：复杂网络节点重要性的排序，复杂网络的风险评估与决策，复杂网络效益的预测。本文重点讨论前两方面的内容，在前文对网络基的概念及其性质研究的基础上，研究粗糙复杂网络上的决策方法。

3.1 粗糙复杂网络节点重要性的排序

方法1设Vi,i=1,2,…,n是RCN顶点集合，ki=分别表示节点i度和介数，把网络节点的重要性作为该节点的权重ωi，且

然后依据ωi的大小对节点排序。

方法2一些实际粗糙复杂网络，网络的构建不太容易，但是根据以往的经验已知它的度分布，或者通过统计调研和回归分析的方法可以确定其度分布和每个节点是属于正域、负域，还是边界域，网络的度分布分别见表1和表2。

假定度相同的节点在网络结构中有着相同的重要性，决策者事先已有一些经验的主观估计权重λ=(λ1,λ2,…,λn)T，定义熵值如式（2），其中i=1,2,…,n：

其中，kmax表示网络度k的最大值；mk表示度为k的节点出现的频数。

Table 1 Degree distribution of underapproximation networks表1 下近似粗糙复杂网络度分布

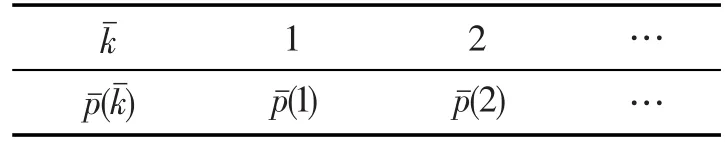
Table 2 Degree distribution of upapproximation networks表2 上近似粗糙复杂网络度分布

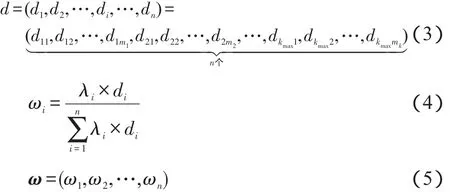
复杂网络中，节点重要性的排序，方法1简单直观，考虑了节点的度和介数两方面的特性，但是要求构造出复杂网络；方法2比较抽象，直接利用粗糙复杂网络的度分布来计算权重，无需构建粗糙复杂网络，也无需构造复杂网络上的决策矩阵，这是比原有的熵值法先进之处。为了避免仅利用度信息而没有充分考虑网络结构的缺陷，在此加入了决策者的主观权重λ=(λ1,λ2,…,λn)T，是对网络结构比较模糊时，网络节点评估方法的有力补充。

3.2 粗糙复杂网络风险评估的决策方法

3.2.1 基于最大度和最大介数的决策法

实际复杂网络中，决策者通常需要一系列的监管策略，降低网络风险，保障网络的稳定和安全。这些实际网络一般都有无标度网络和小世界网络的特征，对随机攻击有着很强的鲁棒性和选择性，意外攻击具有明显的脆弱性的特点。因此，网络维护和网络攻击的目光都在于最大度节点和最大介数节点。这种方法简单，容易操作和实现，网络维护者只需按照合适的比例分配人力、物力和财力给最大度节点和最大介数节点。分配比例系数的确定可以转化为最优化问题（6）的解，最优化问题（6）可以通过非线性规划法求解。

其中，fi(V)为节点i的风险评估函数；α1、α2为决策变量。

这种方法最大的弊端是仅仅关注了网络最大度节点和介数节点，忽略了网络的基本结构。鉴于此，提出了基于网络基的粗糙复杂网络风险评估的决策方法。

3.2.2 基于网络基的风险评估决策法

粗糙复杂网络中存在着大量的不完全信息和不可分辨性的数据，为了决策的科学化和规范化，本文提出了基于网络基的风险评估决策法，达到风险最小化的目的。其基本思想和决策步骤如下：

（1）运用粗糙集属性规则的提取原理[11,14]，删除冗余属性和无效节点。

（2）构建有效节点的属性集V=(V1,V2,…)和风险评估函数；gi(Vi,α),α=(α1,α2,…,αj),i=1,2,…,i表示第i个节点，j表示网络的风险因子的数目。

（4）在网络基节点中，任取一个节点为源节点，运用Dijkstra算法确定其到其余节点的最短路径，给出网络基节点的Njl(i)。

（5）建立基于网络基的多目标最优化决策模型（7），确定风险因子α=(α1,α2,…,αj)，α为决策变量：

（6）运用线性加权法将多目标最优化（7）转变为数学规划（8），由此得该决策问题的最优解。

建立网络基的邻接矩阵A，根据特征向量法确定网络基节点的权重 β=(β1,β2,…,βs)，满足Aβ=λmaxβ，因此多目标最优化问题的解转化为式（8）的解：

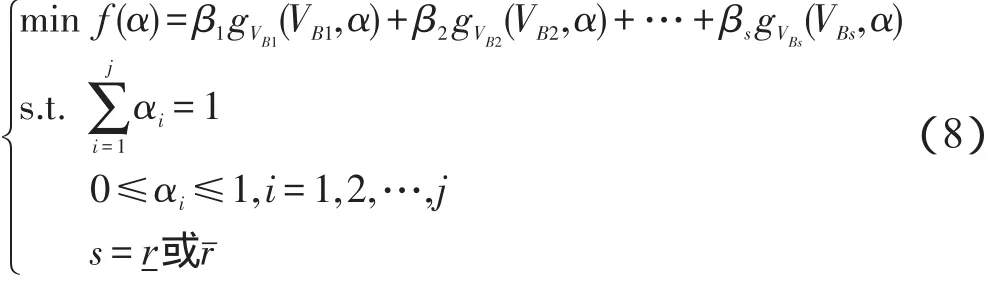
式（8）的解，即为式（7）的近似最优解。

（7）对于粗糙复杂网络RCN，分别求下近似粗糙复杂网络和上近似粗糙复杂网络的最优解，再依据风险型决策法在中做决策。

该方法以网络基与复杂网络具有相同的网络鲁棒性和脆弱性为依据，通过网络基的风险最小化，实现复杂网络风险因子的评估。在决策方法设计中，关于网络基节点的选择，本文根据节点重要性由高到低选取s个线性无关的节点；由网络基邻接矩阵确定网络基节点的权，充分考虑到网络结构的特性。基于网络基的复杂网络决策法的流程图如图1所示。

4 基于网络基的决策法在第三方支付风险管理中的应用

随着“互联网+”的兴起，“互联网+金融”的研究也掀起了一股热潮。作为互联网金融研究热点之一，第三方支付问题的研究，对互联网经济起着至关重要的作用。遗憾的是现有的研究成果都只是一些定性化的结论，没有从复杂网络特性的角度来研究第三方支付风险问题的有关结论与文献。考虑到第三方支付平台交易是以信息网络为媒介，具有粗糙复杂网络的特点，本文运用基于网络基的决策方法，优化第三方支付的风险管理。

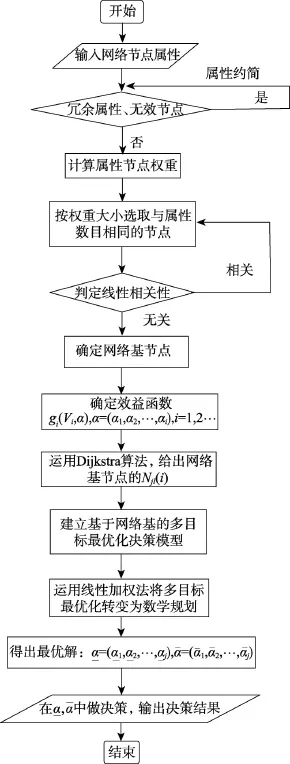
Fig.1 Decision methods of rough complex networks based on network-based图1 基于网络基的复杂网络决策法的流程图

4.1 问题的描述与模型的建立

现有研究表明[16-17]，第三方支付平台经营的风险主要有法律风险、金融风险、市场风险、信用风险和

步骤1寻找网络基，确定邻接矩阵。

在第三方支付粗糙网络中，节点的属性主要有节点的度、节点的权重、路过节点i的最短路径的条数、节点的价格、销售量、收藏量、商品评价等级、商家信用。其中商品评价等级和商家信用采用0～5分制，第i个节点的属性记为：。如果R(V)=s<7，则添加7-s个节点重新计算；否则为网络基节点。重复以上过程直到找到网络基终止，记录该网络基的邻接矩阵。

步骤2确定风险评估函数。

第三方支付平台的风险主要有法律风险、金融风险、市场风险、信用风险和网络技术风险。法律风险是指第三方支付企业性质界定不清，法律责任不清，法律地位不明；目前政府职能部门对此的管制方式是给予一定的罚金G1，法律风险的发生服从参数为λ1的泊松分布，，则法律风险函数为：

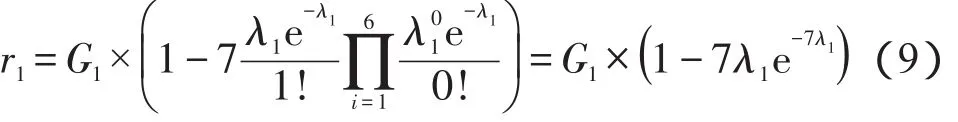
其中，X1为一段时间内网络基节点法律风险发生的次数；G1为常量；λ1为决策变量。

金融风险是指沉淀资金风险、套现风险、洗钱风险、流动性风险。套现风险和洗钱风险一旦发现，就会被勒令禁止并给予一定的处罚，平台管理者会将此风险转嫁给经营的商家；沉淀资金风险和流动性风险的一旦发生，就会危机平台的生存。在周期T内平台的寿命服从参数为θ的指数分布，设沉淀资金的金额为G2，T内的营业额为sum1，则金融风险函数为：

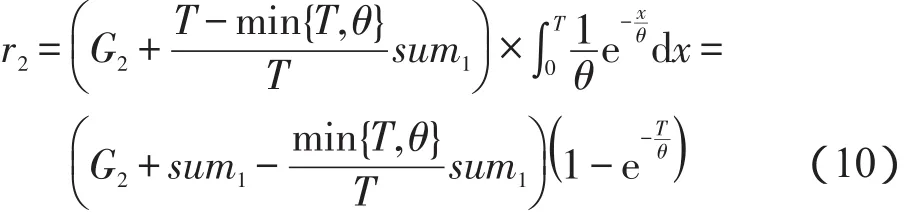
其中，sum1、G2为常量；θ为决策变量。

市场风险是指来自客户方面的风险（客户流失风险）、来自银行方面的风险（银行撤出第三方支付平台，或者银行进入该行业）、来自同行业现有竞争者的风险。第三方支付平台的管理者为了避免市场风险的发生，必然要采取一些措施支付相应的成本降低风险，这些成本即为第三方支付平台的市场风险，记为r3。平台的管理者为了避免市场风险，会提高服务质量的同时制定一系列让利措施，给银行让利率为rate1，减少商户的广告费用比率为rate2。设原广告费用为G，平台营业的原利率为rate0，则市场风险函数为：

信用风险是指买方的违约风险、卖方的违约风险和网络舆情信用传播风险。如果卖方不按时发货或者发的货不是顾客想要的商品，或者买方收到了商品而无理由退换货，此时平台管理者需要支付双份的快递费用。设每单快递费为G3元，每个节点销售的单数为ni,卖方和买方违约次数服从参数为ni,的二项分布。

为控制与扩散舆情需要的奖励金额由惩罚金额来分配，不纳入信用风险函数，则：

其中，G3和ni为常量；λ2为决策变量。

网络技术风险是第三方支付复杂网络的脆弱性造成的网络故障，故障维修时间为t，故障发生时平台管理者的损失函数为；故障发生的次数服从参数为λ3的泊松分布，则网络技术风险函数为：

其中，T为常量；t、λ3为决策变量。

对于网络上的不同节点，网络技术风险可能不同，销售量大的发生金融风险的可能性要大得多，因此网络的风险评估函数定义如下。

步骤3确定二层决策模型。

根据式（14）、（15），分别建立第三方支付粗糙复杂网络风险评估的一层决策模型，λ1、θ、rate1、rate2、λ2、t、λ3为决策变量：

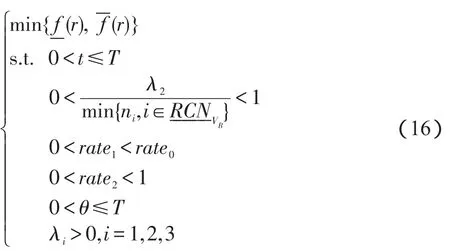
把一级决策变量λ1、θ、rate1、rate2、λ2、t、λ3的近似最优值点代入式（9）、（10）、（11）、（12）、（3），得r=(r1,r2,r3,r4,r5)，从而二级决策变量为：

这里的一级决策变量表示平台管理者对平台的5种风险因子量化的监管控制，二级决策变量表示5种风险因子在平台风险管理中的重要性。

4.2 应用举例与模型的求解

4.2.1 第三方支付粗糙网络的网络基与邻接矩阵的确定

在文献[13]建立的第三方支付粗糙复杂网络中，以2016年1月6日9：00—12:00时淘宝支付平台“天猫商城”4个品牌的商品共136款手机及其相互连接的复杂网络作为研究对象，收集上近似复杂网络节点和下近似复杂网络节点的属性集，其中有效的上近似网络节点有79个，有效的下近似网络节点有52个。该粗糙复杂网络的精确度αR(X)=52/79=0.658，图2[13]是它的下近似复杂网络图，该网络度分布以及mk如表3所示。

图2中，网络节点的属性见表4的第2～8列，其中主观权重λi是专家打分所得，表示节点在网络中重要性的主观判断。

根据本文4.1节中节点重要性排序方法2，可计算出这52个节点的客观权重ωi，见表4的最后一列。根据ωi由大到小选择7个节点{红米Note3，小米4C，红米Note2，三星Galaxy Note 4，三星Galaxy A5(2016)，苹果iPhone 6s，苹果iPhone 6s Plus}，其属性集为：

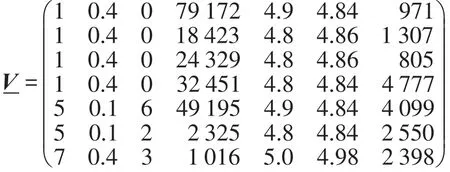
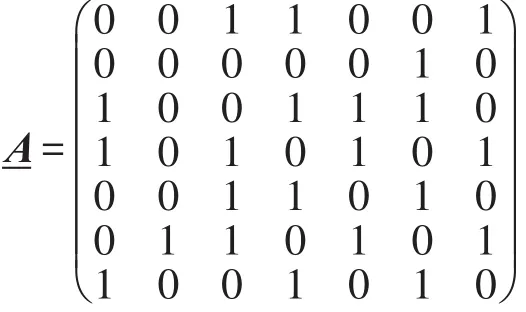
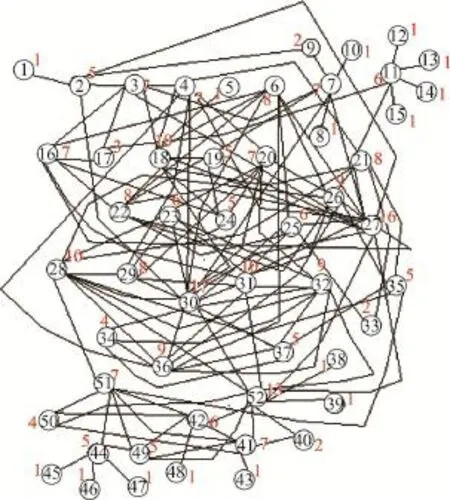
Fig.2 Under-approximately networks of the third-party payment图2 第三方支付的下近似网络

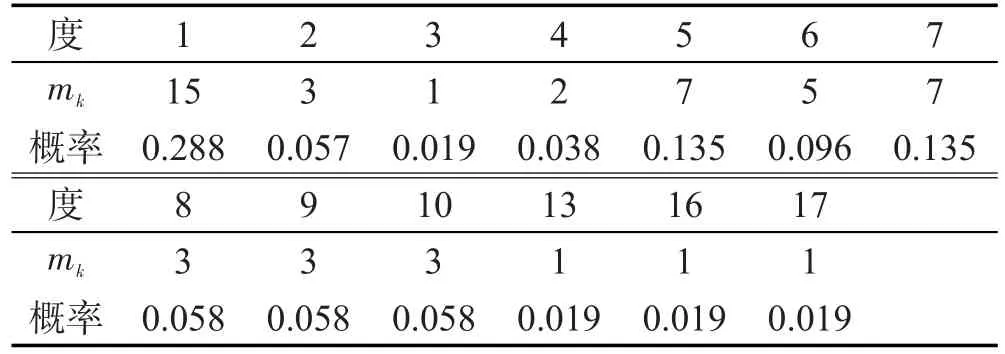
Table 3 Probability distribution table of nodes in Fig.1表3 图1中的节点概率分布表

Table 4 Objective weights and attributes of nodes in under-approximate rough complex networks表4 下近似复杂网络节点的属性与客观权重

由邻接矩阵，绘制下近似粗糙复杂网络的网络基，见图3。网络基中节点的见表5。

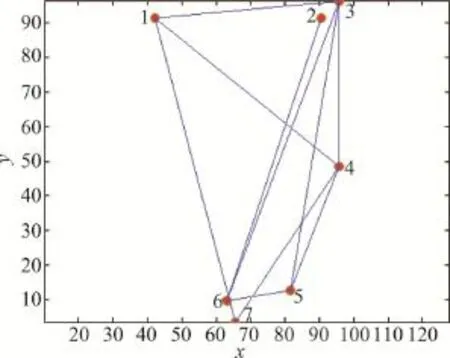
Fig.3 Network bases of under-approximate rough complex networks图3 下近似粗糙复杂网络的网络基

Table 5 Shortest path number of passing nodesiin under-approximate network bases表5 下近似网络基路过节点i的最短路径数

4.2.2 基于网络基的粗糙复杂网络二层决策模型的求解

根据银监会关于电子商务管理的有关规定，以T个单位时间为周期，给常量赋值：G1=10万，G2=20万，rate0=0.05,G=1万，sum1=30万，G3=0.002万，T=24h，将这些常量代入式（14）、（15）得到一层多目标决策模型：

Fig.4 Up-approximate rough complex networks of the third-party payment图4 第三方支付上近似粗糙复杂网络

Fig.5 Network bases of up-approximate rough complex networks图5 上近似粗糙复杂网络的网络基

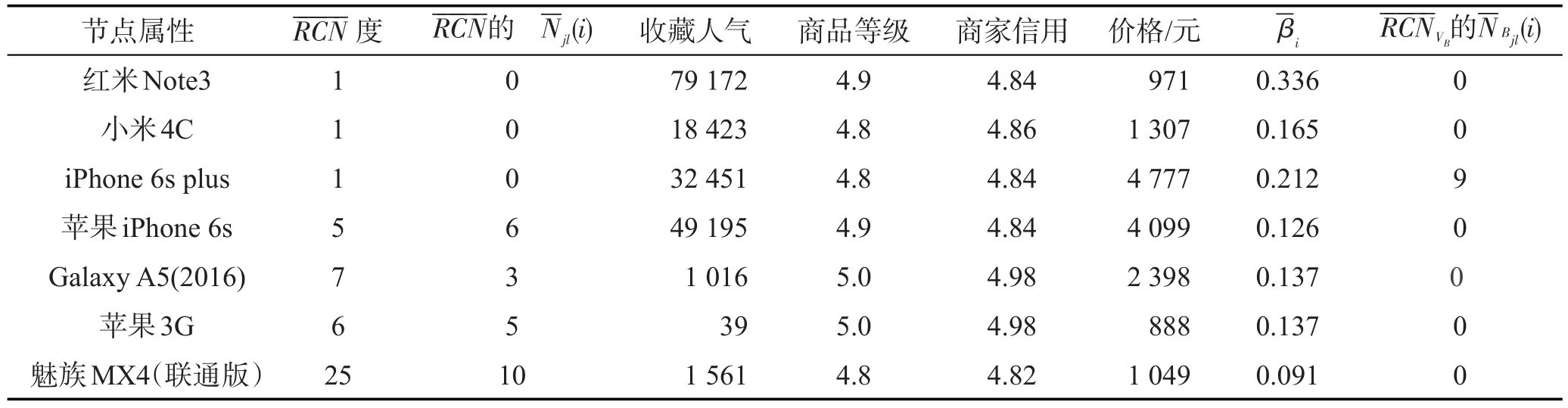
Table 6 Attributes of network bases in up-approximation rough complex networks表6 上近似粗糙复杂网络的网络基属性

利用lingo软件，方程（17）的解为：

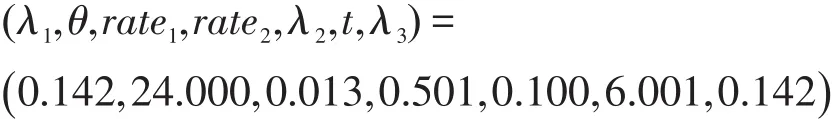
方程（18）的解为：

根据乐观主义风险型决策法，一层决策模型的解为：

即在一天之内，管理者将法律风险发生数目的平均值控制在0.142个，不发生金融风险，给银行让利率为1.3%，给商家降低广告费用为50.1%，退换货的概率控制在0.100，网络技术风险发生次数的平均值控制为0.142次，网络技术风险一旦发生，维修的时间控制在6.001 h之内。

把一级决策变量λ1、θ、rate1、rate2、λ2、t、λ3的近似最优值点代入式（9）、（10）、（11）、（12）、（13），得二级决策变量：

由此得知，这5类风险的重要性排序依次为：金融风险、网络技术风险、法律风险、信用风险、市场风险。

对国内某最大的C2C交易平台进行实际调研和抽样统计，结果表明：平台交易退款笔数控制在交易总数6%以内，法律风险控制在1/7，网络故障发生尽可能在6 h内恢复，尽量避免金融风险的发生，客服必须要学会主动引导卖家给予比较好的评价评分，服务综合得分直接决定商城店铺商品及服务质量。这与本文的实验数据基本趋于一致，说明了本文的研究结果是比较合理的。

5 结束语

粗糙复杂网络具有网络节点的不确定性，连接边信息的不完全性，网络结构复杂，连接关系复杂等特性，因此目前还没有见到粗糙复杂网络决策方法的相关研究成果。本文首先通过知识约简和属性规则的提取实现了对粗糙复杂网络中大量的冗余信息、不完全信息和错误信息的预处理，提高了信息的有效性和可信度。其次，对信息预处理后的粗糙复杂网络，通过两个精确网络来近似，将粗糙复杂网络问题转化为复杂网络问题来研究。考虑到复杂网络依然存在节点的复杂性、结构的复杂性等特点，提出了网络基的概念，并给出了网络基所满足的各种性质，得出了网络基与复杂网络等价的结论，为通过网络基来研究粗糙复杂网络的决策方法奠定了理论基础。第三，给出了复杂网络上节点重要性排序的两种方法和基于网络基的粗糙复杂网络决策方法。第四，通过第三方支付粗糙复杂网络风险问题的研究，建立了基于网络基的第三方支付粗糙复杂网络的决策模型。仿真实例表明，本文的理论研究与决策方法可行。

本文的研究，理论上不仅给出了粗糙复杂网络的网络基的概念和性质，而且提出了基于网络基的粗糙复杂网络的决策方法。在应用上，基于网络基的第三方支付粗糙复杂网络的决策方法的研究，实现了第三方支付平台的风险分析与控制，为平台的管理者提供了定量化的决策参考。

[1]Wang Xiaofan,Li Xiang,Chen Guanrong.Introduction to network science[M].Beijing:Higher Education Press,2012: 3-8.

[2]Guo Shize,Lu Zheming.Basic theory of complex networks [M].Beijing:Science Press,2012:303-319.

[3]Liu Jianxiang.Overview of complex networks and the progress of national research[J].Systems Science,2009,17(4): 31-35.

[4]Zhou Tao,Bo Wenjie,Wang Binghong,et al.Overview of complex networks[J].Physics,2005,34(1):31-36.

[5]Wang Jinna,Shi Lei.Research on the third-party logistics distribution decision model[J].The South of China Today, 2009(6):11-13.

[6]Zhao Fenghua,Yang Bo.Comprehensive evaluation on identifying key nodes in complex networks[J].Journal of Wuhan University of Technology:Information＆Management Engineering,2015,37(4):461-464.

[7]Liu Jun,Xiong Qingyu,Shi Weiren,et al.Evaluating the importance of nodes in complex networks[J].Physica A: Statistical Mechanics and Its Applications,2016,452:209-219.

[8]Gómez C,Sánchez-Silva M,Dueñas-Osorio L,et al.An applied complex systems framework for risk-based decisionmaking in infrastructure engineering[J].Structural Safety, 2014,50:66-77.

[9]Stalidis G,Karapistolis D,Vafeiadis A.Marketing decision support using artificial intelligence and knowledge modeling: application to tourist destination management[J].Social and Behavioral Sciences,2015,175:106-113.

[10]Ferretti S.Gossiping for resource discovering:an analysis based on complex network theory[J].Future Generation Computer Systems,2013,29(6):1631-1644.

[11]Zhang Wenxiu,Wu Weizhi,Liang Jiye,et al.Rough set theory and methods[M].Beijing:Science Press,2001:3-10.

[12]Bo Zhongkui,Yang Shanlin.Rough decision analysis model based on the new features dominance relations[J].Statistics and Decision,2015(1):41-44.

[13]Cao Lixia,Huang Guangqiu,Li Yan.Study on the third-party payment rough complex network knowledge discovery methods[J].Journal of Frontiers of Computer Science and Technology,2016,10(8):1143-1153.

[14]Yu Ying,Miao Duoqian,Zhao Cairong,et al.Knowledge acquisition methods for multi-label decision system based on rough sets[J].Journal of Frontiers of Computer Science and Technology,2015,9(1):94-104.

[15]An Liping.Multi-attribute decision analysis based on rough set theory[M].Beijing:Science Press,2008:45-47.

[16]Zhu Shanhong,Kuang Tao.E-commerce model and platform based on the third-party[J].Journal of Chemical and Pharmaceutical Research,2014,6(3):863-868.

[17]Rong Ling.Research on the third-party payment platform industry regulation and competitive strategy[D].Shanghai: Fudan University,2012.

附中文参考文献：

[1]汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012:3-8.

[2]郭世泽,陆哲明.复杂网络基础理论[M].北京:科学出版社,2012:303-309.

[3]刘建香.复杂网络及其在国内研究进展的综述[J].系统科学学报,2009,17(4):31-35.

[4]周涛,柏文洁,汪秉宏,等.复杂网络研究概述[J].物理, 2005,34(1):31-36.

[5]王锦娜,石磊.第三方物流企业配送决策模型研究[J].今日南国,2009(6):11-13.

[6]赵凤花,杨波.复杂网络节点重要性的综合评价方法[J].武汉理工大学学报:信息与管理工程版,2015,37(4):461-464.

[11]张文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2001:3-10.

[12]鲍忠奎,杨善林.基于新特征优势关系的粗糙决策分析模型[J].统计与决策,2015(1):41-44.

[13]曹黎侠,黄光球,李艳.第三方支付粗糙复杂网络知识发现方法研究[J].计算机科学与探索,2016,10(8):1143-1153.

[14]余鹰,苗夺谦,赵才荣,等.基于粗糙集的多标记决策系统知识获取方法[J].计算机科学与探索,2015,9(1):94-104.

[15]安利平.基于粗糙集理论的多属性决策分析[M].北京:科学出版社,2008:45-47.

[17]容玲.第三方支付平台竞争策略与产业规制研究[D].上海:复旦大学,2012.

CAO Lixia was born in 1971.She is a Ph.D.candidate at School of Management,Xi’an University of Architecture and Technology,and an associate professor at Xi’an Technological University.Her research interests include rough set,complex network,operation research and cybernetics,management decision analysis and game theory,etc.

曹黎侠（1971—），女，陕西西安人，西安建筑科技大学管理学院博士研究生，西安工业大学副教授，主要研究领域为粗糙集，复杂网络，运筹学与控制论，管理决策分析及博弈论等。

HUANG Guangqiu was born in 1964.He is a professor and Ph.D.supervisor at School of Management,Xi’an University of Architecture and Technology,the consultant expert of the Government of Xi’an,and the assessment expert of National Natural Science Foundation.His research interests include e-business and network security,information management,systems engineering,complex system simulation and control,decision optimization and management,etc.

黄光球（1964—），男，西安建筑科技大学管理学院教授、博士生导师，西安市专家咨询团特聘专家，国家自然科学基金项目评审专家，教育部博士点基金项目评审专家，管理科学与工程以及计算机科学技术领域权威期刊审稿专家，主要研究领域为电子商务与网络安全，信息管理，系统工程，复杂系统仿真与控制，决策优化与管理等。

LI Yan was born in 1984.He is a Ph.D.candidate at School of Management,Xi’an University of Architecture and Technology,and the member of CCF.His research interests include information confrontation,network security and systems engineering,etc.

李艳（1984—），男，蒙古族，河北承德人，西安建筑科技大学管理学院博士研究生，CCF会员，主要研究领域为信息对抗，网络安全，系统工程等。

Decision Methods andApplications of Rough Complex Networks Based on Network-Basedƽ

CAO Lixia1,2+,HUANG Guangqiu1,LI Yan1
1.School of Management,Xi’an University ofArchitecture and Technology,Xi’an 710055,China
2.School of Science,Xi’an Technological University,Xi’an 710032,China
+Corresponding author:E-mail:caolx_8@163.com

In some real complex networks,to maximize interests and minimize their own risk,networks managers will face making some decisions,but the existing researches are against a kind of network to making-decision,and lack of versatility,also ignore a large number uncertain phenomenon in complex networks,it is difficult to obtain good decision.This paper defines network-based of rough complex networks,studies the natures of network-based,and proves the conclusion of complex network equivalent its network-based.Then this paper proposes two decision methods about nodes importance and decision methods of rough complex networks based on network-based.Finally this paper uses the decision methods based on network-based in the risk decisions of the third-party payment rough complex networks,establishes a risk decision model,and gives quantitative decision results.The decision methods based on network-based are used successfully in the risk decision model of the third-party payment rough complex networks, which show the effectiveness and feasibility of decision methods.

rough complex networks;network-based;decision methods;the third-party payment risk analysis

10.3778/j.issn.1673-9418.1604050

A

TP182；N945.25

*The Natural Science Basic Research Program(Key)of Shaanxi Province under Grant No.2015JZ010(陕西省自然科学基础研究计划(重点));the Special Research Plan Project of Education Department of Shaanxi Province under Grant No.16JK1369(陕西省教育厅科学计划研究项目).

Received 2016-04,Accepted 2016-06.

CNKI网络优先出版:2016-06-02,http://www.cnki.net/kcms/detail/11.5602.TP.20160602.1506.014.html