结合群体协同与和声搜索策略的果蝇优化算法*
2016-11-22刘乐
刘 乐
济南大学 管理学院,济南 250002
结合群体协同与和声搜索策略的果蝇优化算法*
刘 乐+
济南大学 管理学院,济南 250002
LIU Le.Fruit fly optimization algorithm by combining strategies of swarm collaboration and harmony search.Journal of Frontiers of Computer Science and Technology,2016,10(11):1587-1600.
为了改善标准果蝇优化(fruit fly optimization,FFO)算法易陷入局部极优,收敛精度不高的不足,提出了一种结合群体协同(swarm collaboration,SC)与和声搜索(harmony search,HS)策略的新型果蝇优化算法FFO-SC+HS。该算法基于随机确定的单一维度和动态搜索半径得到果蝇个体的食物源位置,并在种群中心位置的逐代更新环节新增了两个可供选择的备选位置。两备选位置均出自按群体协同策略重构后的位置集合,其一为重构后位置向量集合中的最佳位置,另一则为借助和声搜索策略得到的新位置向量。为验证所设计算法的有效性,在10种测试函数上进行了大量的计算实验与性能对比分析,结果表明FFO-SC+HS在求解质量、收敛能力上优于其他4种已报道的FFO算法,并发现3个主要参数的不同取值组合对其优化性能具有显著影响,所采取的SC与HS策略缺一不可。
果蝇优化;群体协同;和声搜索;函数优化
1 引言
果蝇优化(fruit fly optimization,FFO)算法由Pan于2011年最早提出[1],是一种受果蝇觅食行为启发的新型群体智能优化技术。自然界中的果蝇通常具备出众的嗅觉与视觉能力,能在所处群体中心位置的基础上自如地确定下一步的觅食步长与方向,从而逐渐向远处的食物源靠近。果蝇优化算法源于对果蝇觅食习性的模仿;面向待优化问题的解空间,它分嗅觉觅食(osphresis foraging)和视觉觅食(vision foraging)两个阶段进行迭代式随机搜索,不考虑求解空间是否连续、可微,无需目标函数的梯度信息。自问世以来,果蝇优化算法凭借流程简单,易于实现,控制参数少(仅2个),易跟其他启发式优化技术相混合等优势,已在财务危机数据分析[2]、参数辨识[3-4]、电子节流阀控制[5]、年度电力负荷预测[6]、双级供应链网络优化[7]、炼钢重调度优化[8]等领域得到成功应用,并为多维度背包[9]、置换流水线调度[10]、随机资源约束项目调度[11]、多产品联合补货[12]等典型NP-Hard问题提供了新颖、高效的求解手段。
标准果蝇优化算法在实际应用中具备不易跳出局部极优,收敛精度不高等缺陷。为此,近年来相继涌现出了若干成功的果蝇优化改进算法。这些算法的改进思路大致分为3类:一是在嗅觉觅食阶段改进果蝇个体获得食物源位置的方式,并引入新的参数及其设置方式,例如基于新解线性生成机制的果蝇优化算法(linear generation mechanism of candidate solution-based fruit fly optimization algorithm,LGMSFOA)[13]、基于“历史认知”的果蝇优化算法(FOA based on history cognition,FOABHC)[14]以及基于随机确定的单维分量与动态搜索半径的改进果蝇优化算法(improved FFO,IFFO)[15]。二是在视觉觅食阶段通过融合先进的启发式优化机理以求不断改善果蝇种群的中心位置,例如基于细菌趋化的果蝇优化算法(bacterial chemotaxis-based FOA,BCFOA)[16]、自适应混沌果蝇优化算法(adaptive chaos FOA,ACFOA)[17]以及基于最优最差个体协同学习的果蝇优化算法(best-worst FOA,BWFOA)[18]等。三是在标准果蝇优化算法框架基础上融合多种群协同进化机制,提出了改进的果蝇优化算法,包括动态双子群协同进化果蝇优化算法(dynamic double subgroups cooperative FOA,DDSCFOA)[19]和新型多种群果蝇优化算法(multi-swarm FOA,MFOA)[3]。相比而言,运用第三类改进思路的果蝇优化算法目前还较少;第一、二类改进思路吸引了更多人的研究兴趣。最近,由Wang等人提出的改良型果蝇优化算法(improved FOA,IFOA)[12]中,前两类改进思路同时得以实施,并取得了令人满意的改进效果。
为了进一步挖掘果蝇优化算法的优化潜力,本文设计了一种新的混合果蝇优化算法,称为“结合群体协同与和声搜索策略的果蝇优化算法”(FFO with swarm collaboration and harmony search strategies,FFO-SC+HS)。该算法在每次迭代过程中面向单维分量生成食物源位置,并通过融合群体协同机制(swarm collaboration,SC)以及和声搜索(harmony search,HS)策略来改进果蝇种群中心位置的逐代更新方式。在现有的诸多改进果蝇优化算法中,IFFO算法[15]、MFOA算法[3]和IFOA算法[12]无论在优化机理上,还是在优化性能上均较标准果蝇优化算法有明显改进。为此,本文以上述3种算法为主要比较对象,在选定的10种测试函数上进行一系列计算实验。实验结果显示,FFO-SC+HS算法在函数优化质量、收敛能力上均具备相对优越性。此外,还基于实验设计方法分析了不同参数取值组合以及两种融合策略对于所提出算法优化性能的影响。
2 标准的果蝇优化算法
果蝇优化算法实质上是一种模拟果蝇嗅觉觅食与视觉觅食行为的迭代式全局搜索方法。数学优化问题的n维求解空间决定着果蝇种群的允许飞行空间;各果蝇个体在n维空间中的所处位置代表已搜索到的解向量。在每次迭代搜索过程中,都要先后经历“嗅觉觅食”与“视觉觅食”两个阶段。敏锐的嗅觉能力使每个果蝇都能从当前种群的中心聚集位置出发,借助一定的觅食步长接近食物源位置。果蝇个体的当前所处位置对应于由优化目标函数所决定的味道浓度(smell concentration)。“视觉觅食”的过程即为从当前果蝇群体中确定味道浓度最佳的果蝇所处位置,如果该位置的味道浓度优于当前群体中心位置,则其他果蝇个体凭借视觉追踪能力向该位置聚集。
对于数学优化问题的界定以及标准果蝇优化算法对其求解的一般步骤可描述如下。

对于待最小化的数学优化问题:其中,n为解空间的维数;X=(x1,x2,…,xn)为解向量;f(⋅)为待优化的目标函数;LBi和UBi分别为决策变量xi取值范围的下界与上界值(i∈{1,2,…,n})。
步骤1初始化控制参数和果蝇群体的中心位置。首先对种群规模Popsize和最大迭代次数Itermax进行初始化。然后,在待搜索的n维空间中按下式随机生成初始的果蝇种群中心位置Δ=(δ1,δ2,…,δn)。

其中,函数rand(S)随机返回集合S的任一元素。
步骤2各个果蝇从当前的种群中心位置Δ出发进行嗅觉觅食搜索,随机得到Popsize个食物源位置。假设Pop={X(1),X(2),…,X(Popsize)}为所生成的食物源位置集合。第p个果蝇飞往的食物源位置;分量可由下式得出:
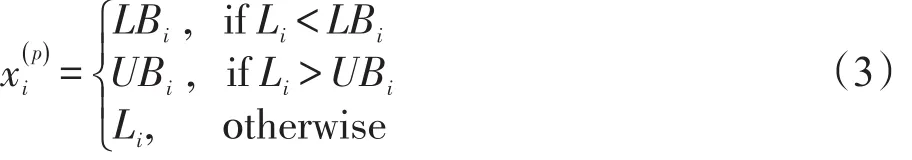
其中,Li=di+rand([-1,1]),i=1,2,…,n。
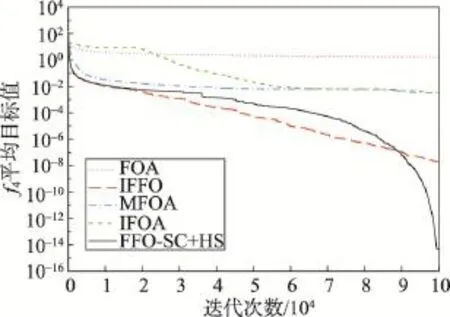
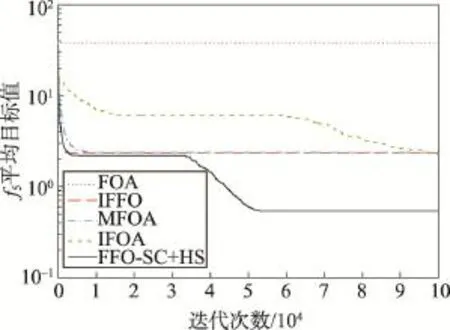
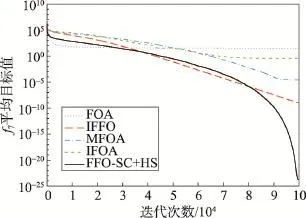
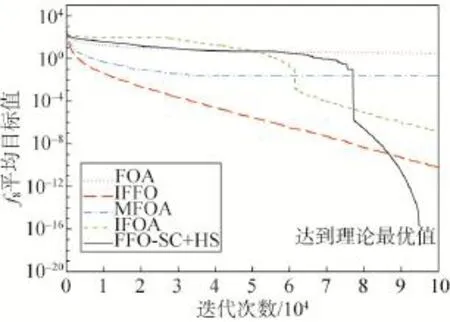
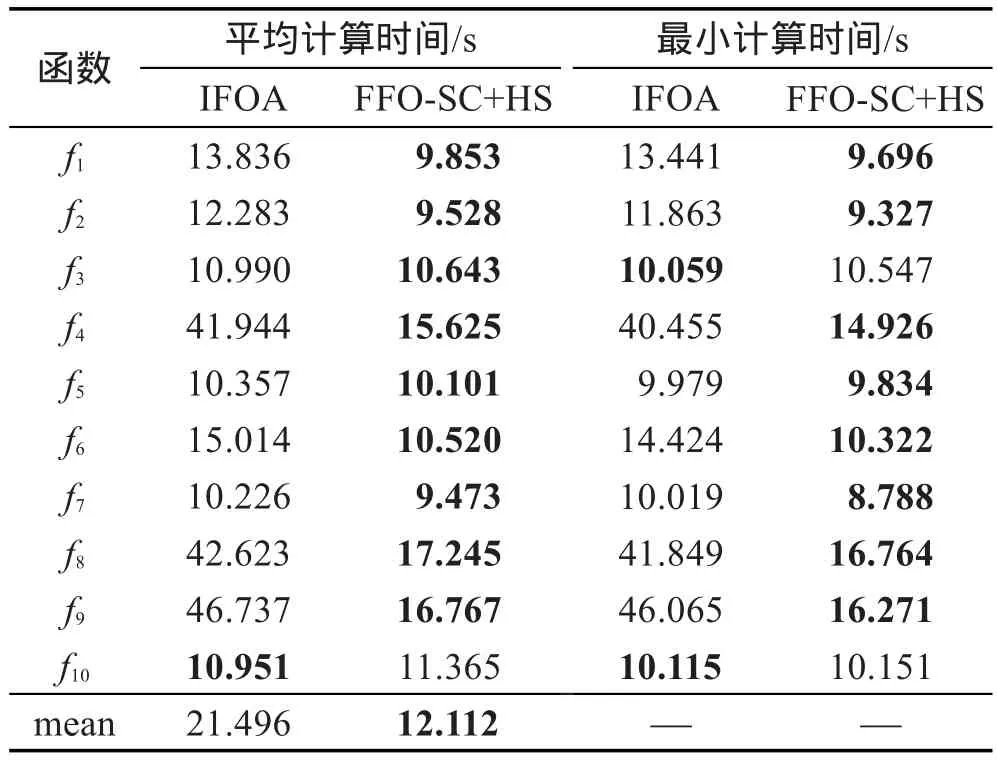
步骤3根据目标函数式 f(⋅)计算各个食物源位置X(p)的味道浓度(p=1,2,…,Popsize),并展开视觉觅食搜索,即将最佳味道浓度所对应的食物源位置作为种群的新中心位置。具体地,首先从当前位置集合Pop中找出具备最小目标值的食物源位置Xbest,即;若 Xbest优于当前种群的中心位置Δ,则Xbest为新的种群中心位置,即Δ←Xbest当且仅当 f(Xbest) 步骤4判断迭代终止条件是否已满足。如果迭代终止准则尚未满足(如未达到最大迭代次数Itermax),则转回步骤2;否则,输出搜索到的最佳食物源位置X*及其味道浓度 f(X*),结束。 相互均衡的集约化(intensification)与分散化(diversification)搜索策略是成功开发出元启发式算法的重要保证。集约化寻优旨在迄今最佳解的邻近区域实施局部搜索,一定程度上会增加求得更好解的概率;但过分追求集约化,易使算法陷入局部极优,弱化全局优化搜索的能力。分散化寻优往往要借助当前种群信息或启发式信息执行覆盖全局的随机化搜索,这样有助于算法摆脱局部极优;但一味注重搜索的分散化,会徒劳地评价许多非最优解,进而影响整体的优化搜索效率。为此,成功的果蝇优化改进算法应实现集约化与分散化搜索之间的有效协调,既要在嗅觉觅食阶段强化集约化搜索的作用,又需在果蝇种群中心位置的更新环节实施专门的分散化寻优机制。 3.1 基于单维分量生成食物源位置 为进一步增强解搜索的集约化程度,算法FFOSC+HS拟在嗅觉觅食阶段采取文献[15]中的相关做法,即基于随机确定的单维分量和动态搜索半径生成果蝇个体的食物源位置。其中,每个新生成的食物源位置跟当前种群的中心位置Δ相比,仅在唯一的分量值上有差别;至于哪一维分量,则由相应的果蝇个体在嗅觉觅食前随机确定;该分量值上的变动幅度将受动态搜索半径的影响。假设为第p个果蝇嗅觉觅食所得食物源位置X(p)的第i维分量(p= 1,2,…,Popsize,i=1,2,…,n),则有: 其中,搜索半径Ri的值适宜随着迭代次数的增加而变小[3,15]。在此拟运用文献[3]中对搜索半径的设置方法,即在第iter次迭代中,Ri(iter)的计算公式为: 结合前期实验结果发现,算法FFO-SC+HS中指数参数ϕ的取值应大于5。 3.2 基于群体协同与和声搜索的分散化寻优 果蝇群体中心位置Δ的更新频次是影响果蝇优化算法求解精度与效率的关键因素。为了促进种群中心位置在逐次迭代中的频繁更新,需要通过引入分散化寻优机制来扩展种群中心位置的择优选取范围。食物源位置集合的结构性变化会引起种群中心位置的不同。为此,在果蝇优化算法的每次迭代中,可考虑对嗅觉觅食阶段形成的位置集合Pop进行自适应重构。重构后的新位置集合既要发挥现有种群中心位置的引导作用,也要体现位置向量的多样性。受文献[12]中成功做法的启发,算法FFO-SC+ HS中拟基于群体协同策略,对由若干食物源位置组成的集合执行重构过程。 重构后的食物源位置集合负责产生若干新的候选中心位置。除了其中具有最小目标值的食物源位置外,还可面向重构后的位置集合,按特定的启发式策略随机生成候选的中心位置。每次迭代中候选的种群中心位置增多,有助于提高中心位置的更新频次,但由于候选中心位置的产生与解质量评价过程均会耗用一定的计算时间开销,扩充的数目不宜过多,否则会影响算法的整体搜索效率。为了确保候选的中心位置少而精,面向重构后位置集合随机生成的候选中心位置应在体现一定随机性的基础上,注重保留重构后位置集合中的历史搜索信息。由此,对于所采取的启发式候选中心位置生成策略,提出了面向群体,对历史搜索信息记忆能力强,易实现,易跟其他元启发式算法相混合的要求。事实上,和声搜索算法就是一种具备上述特征的元启发式优化技术。该技术由Geem等人于2001年最早提出[20],根源于现实中的乐队即兴创作过程。目前,它已在特征选择、钢架结构设计、储能系统研发、单元式制造系统调度等领域得到广泛应用[21-24]。由此,在算法FFO-SC+HS中拟基于重构后的位置集合,运用和声搜索策略随机生成一个候选中心位置,以助于提升种群中心位置的更新幅度与频次。 需要指出的是,在算子Pop_SC_HS_X3中,果蝇种群规模Popsize的值即为参数HMS的取值;和声记忆思考率HMCR∈(0,1),在多数HS算法中建议它选取接近于1的较大值;微调幅度BW由当前搜索半径Ri(iter)所决定。此外,结合先期实验结果,拟沿用文献[25]中的方式动态设置参数PAR的值,即以PARmax和PARmin为上、下限,以(PARmax-PARmin)/Itermax为步长而逐代线性递增。 3.3 算法步骤 步骤1对待优化问题、控制参数进行初始化,并置迭代计数变量iter←1。其中,需初始化的参数包括Popsize、ϕ、HMCR、PARmin、PARmax、Itermax。 步骤2按式(2)对果蝇种群的中心位置进行初始化,得到位置向量Δ(0)。 步骤3各个果蝇从种群中心位置Δ(iter-1)出发,基于随机确定的单维分量和动态搜索半径按式(4)和式(5)进行嗅觉觅食搜索,得到位置集合Popiter。其中,搜索半径Ri(iter)的值按式(6)确定。 步骤4从位置集合Popiter中找出具备最佳味道浓度(目标函数值)的食物源位置,并将其作为备选的新种群中心位置,即。 步骤5运用算子Pop_SC对集合Popiter进行群体协同式重构,得到新位置集合。 步骤9置iter←iter+1。若iter≤Itermax,则转回步骤3;否则,将Δ(Itermax)作为最终解输出,结束。 对于算法FFO-SC+HS的计算复杂性分析如下。步骤1对优化问题和控制参数进行初始化,消耗常数时间O(1)。步骤2对种群中心位置进行初始化,消耗O(n)时间。步骤3~9重复执行Itermax次。在每次迭代中,步骤3负责实施嗅觉觅食搜索,需耗用O(Popsize×n)时间;步骤4从集合Popiter中确定备选中心位置,需消耗O(Popsize)时间;步骤5、6和7的计算时间分别由算子Pop_SC、Pop_SC_X2和Pop_SC_HS_X3所决定;步骤8和9均耗用常数时间O(1)。算子Pop_SC的计算时间为O(Popsize×n),如算法1所示;算子Pop_SC_X2的计算时间为O(Popsize),如算法2所示;算子Pop_SC_HS_X3的计算时间为O(n),如算法3所示。综上,算法FFO-SC+HS的总体时间复杂度可归结为O(Itermax×Popsize×n)。 4.1 计算实验准备与相关描述 为了考察、评估FFO-SC+HS算法在函数优化问题求解上的有效性,本文选取10种无约束的最小化函数进行测试。这10种测试函数可区分为3类:单模态基准函数 f1~f3;存在多个极值的多模态基准函数 f4和 f5;对常见基准函数的决策变量进行偏移后而得到的变换型(Shifted)函数 f6~f10。后5种函数出自“商务与企业计算(commerce and enterprise computing,CEC)”2010标准测试函数集[26]。经变量偏移后,这些函数的最优值点不再处于搜索空间的中央位置,而出现在边界或若干狭小区域中,从而增加了最优解的搜索难度。经变换后的测试函数又有可分离(separable)与不可分离(non-separable)函数之分;通常,可分离函数优化问题求解起来相对容易,完全不可分离函数最难优化。测试函数 f6~f10中,f6~f8为可分离函数,而 f9和 f10为完全不可分离函数。对上述10种测试函数按模态类型划分,f1~f3,f6~f7为单模态(unimodal)函数;f4~f5,f8~f10属于多模态(multimodal)函数。表1给出了10种测试函数的表达式、解搜索空间和各自的理论最优值。 整个计算实验在处理器为Intel®CoreTMi3,主频为2.53 GHz,内存为2.0 GB,操作系统为Windows 7 SP1的PC机上进行。实验中所涉及的各种果蝇优化算法均采用Java语言编程实现。 4.2 算法优化性能比较与分析 为验证FFO-SC+HS算法在函数优化质量、收敛能力上的优越性,拟在表1中的10种测试函数上对其进行性能对比分析。除了算法FFO-SC+HS外,参与优化性能对比的果蝇优化算法有标准FOA算法[2]、IFFO算法[15]、MFOA算法[3]和最近问世的IFOA算法[12]。5种果蝇优化算法的迭代搜索过程都涉及最大迭代次数Itermax的设置。考虑到实验比较条件的公平性和对于解搜索空间维度的依赖性,结合先期计算实验结果,规定各果蝇优化算法的最大迭代次数统一取Itermax=2n×103。此外,参考现有文献中的相关做法,5种果蝇优化算法在该性能对比实验中的其他参数设置详情如下:(1)对于果蝇种群规模,在算法FOA、IFFO和FFO-SC+HS中均取Popsize=10,在算法MFOA中取Popsize=30,而在算法IFOA中取Popsize=50;(2)算法IFFO中搜索半径最小值λmin= 10-5,搜索半径最大值λmax=(UB-LB)/2,其中UB和LB分别为算法搜索范围中各维度上的上限、下限值;(3)在算法MFOA中,子群体的数目M=5,指数参数ϕ=6;(4)算法IFOA中,对扰动放大因子取w=0.3,定位区间LR=[LB,UB],随机飞行的方向与距离区域FR=[(LB-UB)/1 000,(UB-LB)/1 000];(5)在算法FFOSC+HS中,取和声记忆思考率HMCR=0.95,音调微调率最小值PARmin=0.01,音调微调率最大值PARmax= 0.99,指数参数ϕ=6。 Table 1 10 test functions and their searching spaces and theoretical optima表1 10种测试函数及其搜索空间、理论最优值 该优化性能对比实验中,参与对比的果蝇优化算法candiFOA∈{FOA,IFFO,MFOA,IFOA,FFO-SC+HS}跟测试函数 fk(k∈{1,2,…,10})联合确定一个实验单元。统一取110种测试函数的维数n=50,由此,Itermax=105。在实验单元(candiFOA,fk)中,算法candi-FOA对测试函数 fk独立优化25次,每次独立优化后,记下当前所得解向量的目标函数值和优化过程所耗用的时间。表2给出了各实验单元中对于所得目标函数值的统计结果。其中,mean、±SD与best分别表示25次解搜索过程所得目标值数据的平均值、标准差和最好值;对于各测试函数上每项统计指标的最佳结果,均以粗体标示。 Table 2 Computational results of 5 fruit fly optimization algorithms over test functionsf1~f10表2 5种果蝇优化算法对测试函数 f1~f10的优化统计结果 由表2可以看出,针对所统计的10×3=30项指标结果,FFO-SC+HS算法在27项指标上的统计结果优于其他4种果蝇优化算法;与之相比,标准FOA、IFFO、MFOA和IFOA算法分别仅在0、2、1、0项指标上的统计结果采用加粗标示,由此显示出算法FFOSC+HS对不同类型的无约束连续函数在求解精度、求解鲁棒性上的相对优越性。对于单模态函数 f1、f7和 f3,FFO-SC+HS算法在求解质量上的比较优势尤为显著。具体地,在指标mean上,次好果蝇优化算法的统计结果分别为FFO-SC+HS算法对应结果的1.429E+15、4.744E+14和9.804E+08倍。对于变换型函数 f6和 f8,算法FFO-SC+HS能稳健地搜索到理论最优值0,展现出了能有效优化更高维度函数 f6或 f8的潜力。虽然在函数 f10的指标mean上,算法FFOSC+HS逊色于IFFO算法,但二者相差不大(数量级一致),且在指标min上它们也有相近的结果。 Fig.1 Convergence curves of 5 FOAs on functionf1图1 5种果蝇优化算法在函数 f1上的收敛曲线 Fig.2 Convergence curves of 5 FOAs on functionf3图2 5种果蝇优化算法在函数 f3上的收敛曲线 Fig.3 Convergence curves of 5 FOAs on functionf4图3 5种果蝇优化算法在函数 f4上的收敛曲线 Fig.4 Convergence curves of 5 FOAs on functionf5图4 5种果蝇优化算法在函数 f5上的收敛曲线 Fig.5 Convergence curves of 5 FOAs on function f7图5 5种果蝇优化算法在函数f7上的收敛曲线 Fig.6 Convergence curves of 5 FOAs on function f8图6 5种果蝇优化算法在函数f8上的收敛曲线 为对比分析FFO-SC+HS算法在迭代收敛性上的表现,根据5种果蝇优化算法对部分测试函数(D= 50)独立优化25次的平均目标值变化趋势绘制了收敛曲线对比图,如图1~图6所示。对于函数 f1、f3和f4,算法FFO-SC+HS在优化搜索的前期、中期未表现出相对更快的收敛速度;然而,迭代次数超过90 000次以后,它开始加速收敛,收敛速度明显超过之前快于它的IFFO算法,并最终实现了更佳的收敛精度,详见图1~图3。“先慢后快”的收敛趋势也出现在算法FFO-SC+HS对函数 f7和 f8的迭代优化过程中。如图5所示,算法FFO-SC+HS的收敛速度在优化搜索早期不及标准FOA算法,到搜索中期又逊于IFFO算法,直到迭代次数达到80 000次后才表现出显著更快的收敛速度。对于函数 f8,FFO-SC+HS算法能通过95 000次迭代稳定地搜索到理论最优解。这一突出表现完全要归功于75 000次迭代后的“瀑布式”快速收敛阶段,详见图6。对于FFO-SC+HS算法在函数优化中的“慢热”收敛趋势,究其原因,可归于它在迭代搜索的后期表现出了相对更强的摆脱局部极优的能力。Pop_SC_HS_X3算子中逐代线性递增的参数PAR取值是导致迭代后期脱离局部极优能力增强的主要原因。事实上,在和声搜索算法中,当参数HMCR取接近于1的较大值时,音调微调率PAR就成了调节全局搜索能力的重要参数;PAR的值越接近于1,对于即兴生成的新和声解而言,它摆脱局部极优的概率就越大。此外,对于函数 f5,算法FFO-SC+ HS表现出比其他4种果蝇优化算法更好的收敛能力;当迭代次数达到约32 000次时,它没继续保持平稳趋势,而是从局部极值中有效脱离,显示出相对更好的全局搜索能力和收敛精度,详见图4。 相比于标准的果蝇优化算法,FFO-SC+HS算法在其视觉觅食搜索阶段额外增加了对于算子Pop_ SC、Pop_SC_X2和Pop_SC_HS_X3的计算时间开销。这3个算子的计算时间复杂度分别为O(Popsize×n)、O(Popsize)和O(n)。不难看出,算法FFO-SC+HS相对于标准果蝇优化算法的额外时间开销跟果蝇种群规模Popsize和待优化问题的求解空间维数n成正比;当果蝇种群规模较大或者待优化问题的求解空间维数较高时,算法FFO-SC+HS在计算时间开销上会明显超过标准的果蝇优化算法。通过对性能对比实验中每次函数优化所耗用的计算时间数据进行统计分析,可以发现算法FFO-SC+HS在10种测试函数上的总体平均计算时间约为标准果蝇优化算法的1.83倍(两算法中均取Popsize=10),甚至在函数 f6上FFOSC+HS算法与标准果蝇优化算法之间的计算耗时比竟高达7.60。然而,算法FFO-SC+HS的额外计算时间开销并非徒劳,随之换来的是比标准果蝇优化算法显著更优的优化精度和收敛稳定性,详见表2中的相关统计结果。 跟其他果蝇优化改进算法相比,算法FFO-SC+ HS在计算时间开销上虽未表现出全方位的比较优势,但也具备一定的竞争性。表3给出了算法IFOA和FFO-SC+HS在相应实验单元中针对平均、最少耗用时间的统计结果。表中结果显示,FFO-SC+HS算法在10种测试函数上的总体平均计算时间仅为标准果蝇优化算法的0.563倍,并且在9种测试函数上的平均计算时间都少于标准果蝇优化算法,在8种测试函数上的最小计算时间比较中均占优。由此,另鉴于它在函数优化质量上的相对优越性(详见表2),可认定FFO-SC+HS算法具备比IFOA算法更高的函数优化效率。 4.3 参数对优化性能的影响分析 本节拟以函数 f1、f4、f6和 f9为实验对象,力求通过探析参数组合(Popsize,HMCR,ϕ)的不同取值下FFO-SC+HS算法的优化表现,进而得到有价值的参数取值建议。在该参数影响分析实验中,测试函数 fk(k∈{1,4,6,9})以及参数Popsize、HMCR和ϕ的特定取值联合确定一个实验单元。对于各测试函数的维度,统一取n=100。对于果蝇种群规模参数Popsize,所考虑的水平值分别为10,20,30,40和50。鉴于多数HS算法都推荐参数HMCR取接近于1的较大值,在此设置HMCR∈{0.85,0.90,0.95,0.99}。结合前期实验中对指数参数ϕ的取值建议,取ϕ∈{10,15,20}。综上,该参数影响分析实验总共由4×5×4×3=240个实验单元组成。在每个实验单元(fk,Popsize,HMCR,ϕ)中,FFO-SC+HS算法对测试函数 fk独立优化30次,以最大函数评价数目Max_FEs=3.0×106为每次独立优化的迭代终止条件。每次独立优化过程中,一旦当前所得解向量的目标值达到指定阈值VTR=10-10,则记下已完成的解向量函数评价数目FEs。根据文献[26]中的建议,若函数评价次数未超过3.0×106,则认为该次独立优化是“成功”的,并据此算出该实验单元所对应的优化成功率(success rate,SR),即: Table 3 Comparison in computational time of IFOA and FFO-SC+HS over functions f1~f10表3 IFOA和FFO-SC+HS在函数f1~f10上的计算时间对比 其中,对于第i次独立优化过程,如果FEsi≤3.0×106,则isSuccessi=1;否则,isSuccessi=0。假设为当前实验单元中全部成功独立优化对于函数评价数目FEs的算术平均值。由此,取期望函数评价比(expected function evaluations ratio,EFER)为该参数影响分析实验的响应指标,计算方式如下: 实验单元(fk,Popsize,HMCR,ϕ)对应的EFER值越小,说明FFO-SC+HS算法在该参数组合下对函数fk的优化性能越佳。图7给出了4种测试函数各自所对应60个实验单元在指标EFER上的统计结果。 通过观察图7可看出,参数组合(Popsize,HMCR, ϕ)的不同取值对FFO-SC+HS算法的函数优化表现具有显著影响,并且ϕ是最主要的影响参数。当指数参数ϕ=15时,无论另两个参数取何值,FFO-SC+HS算法在指标EFER的表现上都比ϕ=10,ϕ=20下的FFO-SC+HS算法明显更优。若不考虑参数ϕ,随着20种参数组合(Popsize,HMCR)的变化,算法FFO-SC+ HS在指标EFER上的表现相对稳定,并无大幅波动;只是在组合(30,0.90)和(40,0.95)下表现出一定的下降趋势。相比而言,组合(30,0.90)下的FFO-SC+ HS算法在整体优化性能上略优于组合(40,0.95)。综上,算法FFO-SC+HS在函数优化中对参数组合(Popsize,HMCR,ϕ)的建议取值为(30,0.90,15)。 4.4 两种融合策略对优化性能的影响分析 为了考察算法FFO-SC+HS中群体协同与和声搜索策略分别对优化性能提高的贡献,本节拟以函数f1、f4、f6、f8和 f9为实验对象,针对单一混合群体协同策略的FFO-SC算法、单一混合和声搜索策略的FFO-HS算法以及FFO-SC+HS算法进行优化性能对比实验与分析。需要注意的是,相比于FFO-SC+HS算法,算法FFO-SC中缺少算子Pop_SC_HS_X3;而算法FFO-HS中则不含算子Pop_SC和Pop_SC_X2,在算子Pop_SC_HS_X3运行时,不再用重构后的食物源位置集合PopSC作为和声记忆库,取而代之的是在嗅觉觅食搜索阶段形成的位置集合Pop。在该策略影响分析实验中,算法candiFOA∈{FFO-SC,FFOHS,FFO-SC+HS}与测试函数 fk(k∈{1,4,6,8,9})联合确定一个实验单元。具体地,对于各测试函数的维度,统一取n=150;算法FFO-SC中不含Pop_SC_ HS_X3算子,无需考虑参数HMCR的取值;参数HMCR在算法FFO-HS和算法FFO-SC+HS中均取建议值0.90;此外,在3种对比算法中,参数Popsize和ϕ均取建议值30和15。在实验单元(candiFOA,fk)中,算法candiFOA对函数fk独立优化30次;以最大函数评价数目Max_FEs=4×106为每次独立优化的迭代终止条件;每次独立优化过程中一旦发现搜索到的解向量目标值已达到指定阈值VTR=10-6,则记下已完成的解向量函数评价数目FEs;若函数评价次数已达到4×106次,而搜索到的解向量目标值仍大于指定阈值10-6,则认定本次独立优化“不成功”。整个策略影响分析实验由3×5=15个实验单元组成;对于每个实验单元,按式(8)统计出它所对应的EFER指标值。图8给出了FFO-SC、FFO-HS和FFO-SC+HS算法在指标EFER上各自对5种测试函数的统计结果。 Fig.7 Performances in terms of EFER changing with different combinations(Popsize,HMCR,ϕ)on 4 test functions图7 4种测试函数上指标EFER的表现随不同参数组合(Popsize,HMCR,ϕ)的变化情况 Fig.8 Results in terms of EFER for FFO-SC,FFO-HS and FFO-SC+HS algorithms on 5 test functions图8 算法FFO-SC、FFO-HS和FFO-SC+HS在5种测试函数上对指标EFER的统计结果 由图8不难看出,算法FFO-SC和FFO-HS在全部5种测试函数的EFER指标表现上均明显逊色于本文提出的FFO-SC+HS算法。具体统计数字显示,FFO-SC+HS算法在5种测试函数的总体EFER指标表现上分别比算法FFO-SC和FFO-HS提高了35.80%和32.25%。可见,无论群体协同还是和声搜索策略都是算法FFO-SC+HS实现其较高优化性能的有效途径,缺一不可。另外,在算法FFO-SC和FFO-HS之间作比较,可发现算法FFO-HS在5种测试函数上的EFER指标值都略优于FFO-SC,由此反映出和声搜索策略在算法FFO-SC+HS中的优化性能改进贡献相对更大。 通过在每轮迭代中对嗅觉觅食与视觉觅食环节进行同时改进,本文设计出一种融合群体协同与和声搜索策略的FFO-SC+HS算法。本文算法的特点主要体现在三方面:一是在嗅觉觅食环节中基于随机确定的单一维度和动态搜索半径生成果蝇个体的食物源位置;二是为了扩展种群中心位置的择优选取范围,运用群体协同机制对果蝇的位置集合进行自适应重构;三是面向重构后的位置集合,运用和声搜索策略生成候选的种群中心位置。针对算法FFOSC+HS在10种测试函数上展开计算实验;与4种已有的果蝇优化算法进行对比,结果显示FFO-SC+HS算法在整体优化质量、鲁棒性、收敛能力上都具备相对优越性。此外,还考察了60种参数组合(Popsize, HMCR,ϕ)的不同取值以及两种融合策略对于FFOSC+HS算法优化性能的影响。通过分析相关实验结果发现:在组合(30,0.90,15)下,算法FFO-SC+HS表现出相对更佳的优化性能;无论群体协同还是和声搜索策略均对FFO-SC+HS算法的改进具有显著贡献。在后续研究中,一方面应着力从理论上揭示FFO-SC+HS算法的收敛性与有效性,并分析参数选取对算法的收敛性影响;另一方面,FFO-SC+HS算法在高维有约束连续优化、困难组合优化、多目标优化等问题中的应用研究需要受到重视。 [1]Pan W T.Fruit fly optimization algorithm[M].Taipei,China: Tsang Hai Book Publishing Co,2011:10-12. [2]Pan W T.A new fruit fly optimization algorithm:taking the financial distress model as an example[J].Knowledge-Based Systems,2012,26:69-74. [3]Yuan Xiaofang,Dai Xiangshan,Zhao Jingyi,et al.On a novel multi-swarm fruit fly optimization algorithm and its application[J].Applied Mathematics and Computation,2014, 233:260-271. [4]Yuan Xiaofang,Liu Yuanming,Xiang Yongzhong,et al.Parameter identification of BIPT system using chaotic-enhanced fruit fly optimization algorithm[J].Applied Mathematics and Computation,2015,268:1267-1281. [5]Wang Sheng,Yan Bao.Fruit fly optimization algorithm based fractional order fuzzy-PID controller for electronic throttle[J]. Nonlinear Dynamics,2013,73(1):611-619. [6]Li Hongze,Guo Sen,Li Chunjie,et al.A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm[J].Knowledge-Based Systems,2013,37:378-387. [7]Mousavi S M,Alikar N,Niaki S TA,et al.Optimizing a location allocation-inventory problem in a two-echelon supply chain network:a modified fruit fly optimization algorithm[J]. Computers and Industrial Engineering,2015,87:543-560. [8]Li Junqing,Pan Quanke,Mao Kun.A hybrid fruit fly optimization algorithm for the realistic hybrid flowshop rescheduling problem in steelmaking systems[J].IEEE Transactions on Automation Science and Engineering,2016,13(2): 932-949. [9]Wang Ling,Zheng Xiaolong,Wang Shengyao.A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem[J].Knowledge-Based Systems, 2013,48:17-23. [10]Zheng Xiaolong,Wang Ling,Wang Shengyao.A hybrid discrete fruit fly optimization algorithm for solving permutation flow-shop scheduling problem[J].Control Theory and Applications,2014,31(2):159-164. [11]Zheng Xiaolong,Wang Ling.An order-based fruit fly optimization algorithm for stochastic resource-constrained project scheduling[J].Control Theory and Applications,2015, 32(4):540-545. [12]Wang Lin,Shi Yuanlong,Liu Shan.An improved fruit fly optimization algorithm and its application to joint replenishment problems[J].Expert Systems with Applications,2015, 42(9):4310-4323. [13]Shan Dan,Cao Guohua,Dong Hongjiang.LGMS-FOA:an improved fruit fly optimization algorithm for solving optimization problems[J].Mathematical Problems in Engineering, 2013,Article ID:108768. [14]Han Junying,Liu Chengzhong.Fruit fly optimization algorithm based on history cognition[J].Journal of Frontiers of Computer Science and Technology,2014,8(3):368-375. [15]Pan Quanke,Sang Hongyan,Duan Junhua,et al.An improved fruit fly optimization algorithm for continuous function optimization problems[J].Knowledge-Based Systems, 2014,62:69-83. [16]Han Junying,Liu Chengzhong.Fruit fly optimization algorithm based on bacterial chemotaxis[J].Journal of Computer Applications,2013,33(4):964-966. [17]Han Junying,Liu Chengzhong.Adaptive chaos fruit fly optimization algorithm[J].Journal of Computer Applications, 2013,33(5):1313-1316. [18]Han Junying,Liu Chengzhong.Efficient fruit fly optimization algorithm with reverse cognition[J].Computer Engineering,2013,39(11):223-225. [19]Han Junying,Liu Chengzhong,Wang Lianguo.Dynamic double subgroups cooperative fruit fly optimization algorithm[J].Pattern Recognition and Artificial Intelligence, 2013,26(11):1057-1067. [20]Geem Z W,Kim J H,Loganathan G V.A new heuristic optimization algorithm:harmony search[J].Simulation,2001, 76(2):60-68. [21]Diao Ren,Shen Qiang.Feature selection with harmony search[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B,2012,42(6):1509-1523. [22]Murren P,Khandelwal K.Design-driven harmony search (DDHS)in steel frame optimization[J].Engineering Structures,2014,59:798-808. [23]Maleki A,Pourfayaz F.Sizing of stand-alone photovoltaic/ wind/diesel system with battery and fuel cell storage devices by harmony search algorithm[J].Journal of Energy Storage,2015,2:30-42. [24]Li Yazhi,Li Xiaoping,Gupta J N D.Solving the multiobjective flowline manufacturing cell scheduling problem by hybrid harmony search[J].Expert Systems with Applications,2015,42(3):1409-1417. [25]Yadav P,Rajesh K,Panda S K,et al.An intelligent tuned harmony search algorithm for optimization[J].Information Sciences,2012,196:42-72. [26]Tang Ke,Li Xiaodong,Suganthan P N,et al.Benchmark functions for the CECƳ2010 special session and competition on large-scale global optimization[R].Hefei:Nature Inspired Computation andApplications Laboratory,USTC,2009. 附中文参考文献: [1]潘文超.果蝇最佳化演算法[M].中国台北:沧海书局, 2011:10-12. [10]郑晓龙,王凌,王圣尧.求解置换流水线调度问题的混合离散果蝇算法[J].控制理论与应用,2014,31(2):159-164. [11]郑晓龙,王凌.随机资源约束项目调度问题基于序的果蝇算法[J].控制理论与应用,2015,32(4):540-545. [14]韩俊英,刘成忠.基于历史认知的果蝇优化算法[J].计算机科学与探索,2014,8(3):368-375. [16]韩俊英,刘成忠.基于细菌趋化的果蝇优化算法[J].计算机应用,2013,33(4):964-966. [17]韩俊英,刘成忠.自适应混沌果蝇优化算法[J].计算机应用,2013,33(5):1313-1316. [18]韩俊英,刘成忠.反向认知的高效果蝇优化算法[J].计算机工程,2013,39(11):223-225. [19]韩俊英,刘成忠,王联国.动态双子群协同进化果蝇优化算法[J].模式识别与人工智能,2013,26(11):1057-1067. LIU Le was born in 1984.He received the Ph.D.degree in management science and engineering from Beihang University in 2013.Now he is a lecturer at University of Jinan.His research interests include intelligent optimization algorithms,production scheduling and rescheduling,etc. 刘乐(1984—),男,山东济南人,2013年于北京航空航天大学获得管理学博士学位,现为济南大学管理学院讲师,主要研究领域为智能优化算法,生产调度与重调度优化等。已发表学术论文10余篇,目前主持国家自然科学青年基金项目、教育部人文社科研究青年基金项目以及山东省优秀中青年科学家科研奖励基金项目等。 Fruit Fly Optimization Algorithm by Combining Strategies of Swarm Collaboration and Harmony Searchƽ LIU Le+ To deal with the drawbacks of trapping in local optimal solutions easily and low convergence accuracy of the standard fruit fly optimization(FFO)algorithm,this paper proposes a novel fruit fly optimization algorithm by combining the swarm collaboration(SC)and harmony search(HS)strategies,named as FFO-SC+HS.In each iteration of FFO-SC+HS,the food source location of each fruit fly is generated based on a single dimension that is randomly determined and dynamic search radius,and two candidate location vectors derived from the reconstructed location set by SC strategy are considered during the update process of fruit fly swarm location.Further,one candidate location is the best one of the reconstructed location set,and the other one is obtained by means of HS strategy.Extensive computational experiments and comparison analysis are conducted upon 10 benchmark functions to validate the effectiveness of FFO-SC+HS.As demonstrated in the results,FFO-SC+HS outperforms other 4 reported FFO algorithms in terms of solution quality and convergence efficiency.Moreover,it is found that different combinations of three main parametershave a significant impact on optimization performances of FFO-SC+HS,and both of the SC and HS strategies are indispensable. fruit fly optimization;swarm collaboration;harmony search;function optimization 10.3778/j.issn.1673-9418.1510034 A TP301.6 *The National Natural Science Foundation of China under Grant No.71501083(国家自然科学基金);the Youth Foundation of Humanities and Social Science Research of Ministry of Education of China under Grant No.14YJCZH098(教育部人文社会科学研究青年基金);the Promotive Research Foundation for Outstanding Young and Middle-Aged Scientists of Shandong Province under Grant No.BS2015ZZ002(山东省优秀中青年科学家科研奖励基金);the Research Foundation of University of Jinan under Grant No. XKY1322(济南大学科研基金). Received 2015-10,Accepted 2015-12. CNKI网络优先出版:2015-12-16,http://www.cnki.net/kcms/detail/11.5602.TP.20151216.1021.004.html3 新型的果蝇优化改进算法
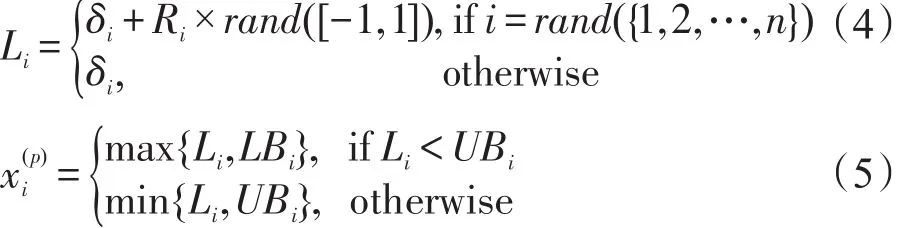





4 实验结果与分析





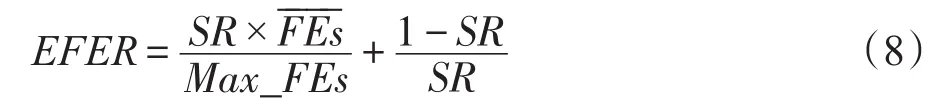

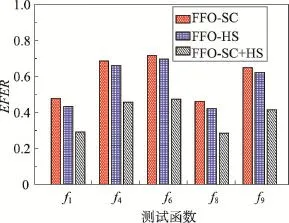
5 结束语

School of Management,University of Jinan,Jinan 250002,China
+Corresponding author:E-mail:sm_liul@ujn.edu.cn
