基于重要性排序蒙特卡洛粒子滤波的物体跟踪算法

许伟村， 赵清杰， 王宇霞， 赵留军

(北京理工大学 计算机科学技术学院，北京 100081)



基于重要性排序蒙特卡洛粒子滤波的物体跟踪算法

许伟村， 赵清杰， 王宇霞， 赵留军

(北京理工大学 计算机科学技术学院，北京 100081)

研究复杂背景下的物体跟踪方法. 提出一种用于物体跟踪的重要性排序马氏链蒙特卡洛粒子滤波算法. 算法利用少量加权初始粒子得到后验概率分布的初步估计，并通过重要性排序马氏链蒙特卡洛采样技术从该初步估计抽取新的粒子，以构建对应不同模态的多条独立马氏链，从而充分逼近真实后验概率分布的多模态. 所提出的算法自适应地根据当前模态分布构建多条独立马氏链，因此能够在多模态的复杂场景下准确估计目标状态的后验概率分布；同时，在构建马氏链的过程中，算法采用重要性排序策略确定历史样本被选为状态转移核的似然度，提高了小权重样本被选中的可能性，降低了在马氏链构建过程中陷入局部最优的概率. 仿真实验以及真实视频上所进行的实验显示，所提出的方法能够实现准确稳定的物体跟踪，且效果优于标准粒子滤波算法以及马氏链蒙特卡洛粒子滤波算法.

目标跟踪；重要性排序；马氏链蒙特卡洛；粒子滤波；多模态

物体跟踪可应用的范围非常广泛，如室内外智能监控系统中对人或车辆的跟踪[1-2]，比赛中对运动员的跟踪[3]等. 贝叶斯连续估计是物体跟踪领域使用最为广泛的技术手段之一，较为常用的有卡尔曼滤波算法和粒子滤波算法，其中粒子滤波算法[4]由于可以简单灵活地处理非线性非高斯问题被广泛使用[5-8]，然而，传统粒子滤波算法的采样效果与产生样本的提议分布以及采样密度相关. 当提议分布与真正的后验概率分布重叠较小将导致较大的状态估计误差，甚至造成跟踪失败. 扩大样本空间同时提高采样密度可保证状态估计精度，但过高的粒子数会导致计算负担过重.

为解决这一问题，部分研究者通过产生更优的提议分布提高采样效率，提出了高斯粒子滤波(Gaussian particle filtering， GPF)[8]，Unsented粒子滤波(Unsented particle filtering， UPF)[10]等算法，其中UPF算法通过Unscented卡尔曼滤波器产生近似后验高斯分布的提议分布，提高了粒子滤波在非线性非高斯系统中的跟踪性能，然而UPF等算法采用的提议分布往往是基于先验统计信息产生的，当目标运动状态与先验统计不符时，仍有可能产生与真实后验分布重叠较小的提议分布，从而导致跟踪漂移甚至失败. 另外一部分研究者则倾向于在采用较优的提议分布的基础上，进一步通过使初次采集的粒子向后验概率峰值区域移动逐步拟合后验分布达到准确跟踪的目的，基于这种思路的代表性算法之一是Gilks等[11]提出的马尔科夫链蒙特卡洛采样粒子滤波(Markov Chain Monte Carlo particle filtering， MCMCPF)算法，这种方法通过MCMC移动使粒子向高置信度区域偏置，最终在状态空间中构造一条平稳分布等于系统状态的后验概率分布的马氏链. MCMCPF及其若干改进算法，如自适应MCMCPF(adaptive MCMCPF， AMCMCPF)算法等[12]，大幅降低了粒子滤波对提议分布的依赖程度，且能够明显提高采样效率. 然而，目标状态的后验概率分布往往由于干扰存在而呈现多模态，此时，MCMCPF容易陷入某个局部最优的干扰模态的峰值区域，从而导致跟踪失败. Maggio等[13]提出的混合粒子滤波(hybrid particle filters， HPF)在采样得到加权粒子集合后，再令每个粒子进行均值偏移，使之向与之最邻近的概率峰值移动，然而，无差别的对所有粒子进行均值偏移可能导致其计算复杂度较高，不能满足实时性要求，且均值偏移过程往往容易陷入局部最优.

本文提出一种重要性排序蒙特卡洛(importance ordering monte carlo， IOMC)粒子滤波算法. IOMC粒子滤波首先从初始提议分布抽取少量加权初始粒子，再进行多次迭代，每次迭代通过重要性排序选择一个权值较高的粒子作为状态转移核以产生新样本，以构建多条独立马氏链. IOMC的采样过程始终在全局样本空间中进行，不会陷入局部最优.

1 基于粒子滤波的物体跟踪

1.1 粒子滤波

物体跟踪问题可以描述为贝叶斯滤波问题. 定义物体在t时刻的状态为xt=(x，y，s)，其中(x，y)表示其中心坐标，s表示其尺度. 假设物体的状态转移服从马尔可夫过程，即

(1)

给定起始时刻至当前时刻t的观测值序列z1:t={z1，z2，…，zt}，贝叶斯滤波通过下式递归地更新目标状态的后验概率密度p(xt|z1:t)：

(2)

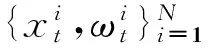
(3)

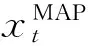
(4)

为得到加权样本集，标准粒子滤波基于重要性采样方法自提议分布q(·)中抽取粒子，并通过递归的方式更新粒子权值. 在一阶马尔科夫假设下，粒子的权值递归更新公式为

(5)

式(5)的具体推导过程可参考文献[4].

1.2 MCMCPF算法

(6)

2 基于IOMC粒子滤波的物体跟踪

复杂场景中由于存在与目标特征相似的背景区域或其他物体，可能在目标可能出现的区域内同时存在多个模态. 由于MCMCPF算法在采样初期无法对每个模态的重要性进行准确估计，导致其采样过程容易陷入局部最优，进而不能充分估计后验分布的每个模态，也无法从中找出真正的目标模态. 为解决这一问题，本文提出重要性排序蒙特卡洛(importance ordering Monte Carlo， IOMC)粒子滤波算法. 算法采用延迟判断的策略，同时创建和充分增长多条独立马氏链，以对所有可能的模态都进行充分拟合逼近，最后再从多个模态中准确选择最优模态. 当场景中仅有一个模态时，IOMC粒子滤波近似于普通的MCMCPF. 另外，传统的权值归一化方法可能造成个别样本权值过高，进而使采样陷入局部最优. 为避免这一问题，以保证每条马氏链都能得到充分增长，在每次迭代中，算法采用重要性排序策略选择作为状态转移核的历史样本. 由于对多模态进行了更充分的逼近拟合，算法能够更为有效的从多模态后验分布中估计后验概率分布.

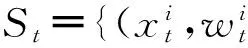
(7)

(8)

集合St中的每一粒子被视作一条独立马氏链的初始样本点，通过Mb(Mb≥Ma)次迭代更新，最终得到多条独立马氏链. 每次迭代中，选择重要性较高的一条马氏链通过MH采样对其进行更新.

(9)

IOMC粒子滤波在t时刻的详细步骤如下所示：

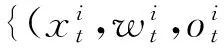
③ 重要性MH采样：

Ⅰ)从均匀分布抽取随机数c～U(1，Ma)，从均匀分布抽取随机数d～U(1，Ma)；

Ⅱ)自索引为c的粒子开始遍历寻找满足以下条件的粒子：

(10)

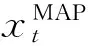
⑤ 执行重要性重采样：

Ⅰ) 归一化粒子权值；

Ⅱ) 消除权值较小的粒子，并复制权值较大的粒子，获得Ma个新样本；

Ⅲ) 为每个再采样之后的样本赋予相同的权值.

实际中，由于拟合同一模态的马氏链在多次迭代后可能重合，在每次迭代后合并重合马氏链以减少马氏链数可以进一步提高IOMC采样的效率. 由于IOMC粒子滤波算法的采样数是固定的数目(Ma+Mb)，因此其运算时间与采用同样粒子数的MCMCPF算法基本相同，并不受模态数或者马氏链数的影响.

3 实验结果与分析

为验证IOMC粒子滤波算法的有效性，进行了仿真实验与真实视频跟踪场景中进行的实验，并与传统粒子滤波算法、HPF算法以及MCMCPF算法进行比对. 在实验中，传统粒子滤波算法、HPF算法和本文算法采用状态转移方程作为提议分布，MCMCPF算法则采用状态预测值作为初始样本. 仿真实验以及真实场景实验中比对算法使用150个粒子，同时令Ma=50，Mb=100.

3.1 仿真实验

人工生成一个非线性非高斯系统，用x0表示系统初始状态，实验中令x0=1;用xt表示系统的当前状态. 系统的状态转移方程和观测方程可分别表示为

(11)

(12)

为分析所测试的算法在仿真实验中的表现，计算每次实验不同算法的根均方差(root mean square error， MRSE)的均值及方差，以测试不同方法状态估计的准确性以及方法的鲁棒性. 其中一次独立实验的根均方差的计算公式为

(13)

图1展示了在一次独立实验中不同算法得到的状态估计值以及真实状态值和虚警；图2展示了不同算法的根均方差. 表1中给出了不同算法的根均方差均值及方差.

由于HPF算法难以用仿真的方式实现，因此仅给出其他3种方法的结果. 由于在仿真实验中存

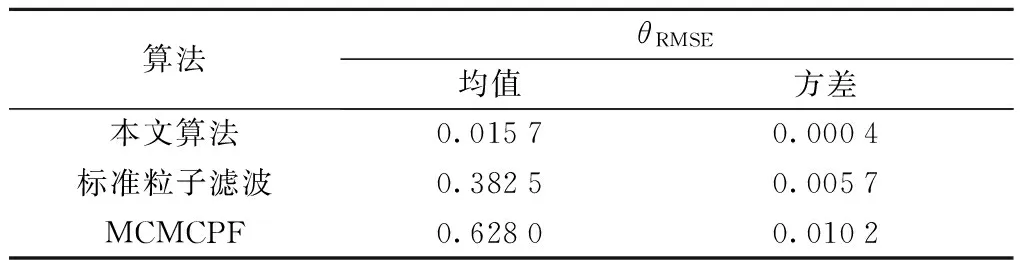
表1 不同算法的根均方差均值及方差

Tab.1 Mean value and covariance of RMSE of different methods

算法θRMSE均值方差本文算法0.01570.0004标准粒子滤波0.38250.0057MCMCPF0.62800.0102

在虚警，因此后验分布中包含了目标模态和干扰模态. 标准粒子滤波算法没有考虑不同的模态，对任何一种模态都没有进行充分逼近；MCMC算法由于容易陷入局部最优，在采样过程中倾向于向单一模态逼近，当所逼近的模态为干扰模态时状态估计精度明显下降；IOMC粒子滤波对两种模态都进行了充分逼近，输出结果为最优模态的值，因此如图中以及表中的结果显示，IOMC粒子滤波的表现明显优于其他两种算法.

3.2 真实场景实验

使用标准数据集中的视频进行真实视频实验. 所测试的算法均采用一阶恒速模型作为状态转移方程，并采用归一化的HSV颜色直方图作为观测模型. 选取数据PETS2009[15]中的低帧率视频“View_001”测试不同算法跟踪突然运动的目标的鲁棒性. 所测试算法皆通过手动初始化. 表2中给出了4种方法的定量分析结果，其中运行速度用算法1 s处理的帧数衡量，成功率为目标被成功跟踪的时长与目标从初始帧至被完全遮挡前出现的总时长的比值.

表2 不同算法的跟踪结果

如表2中所示，本文算法以及HPF的跟踪成功率明显高于粒子滤波算法和MCMCPF算法，但是HPF算法运行速度较低，不能满足实时性需求.

图3给出了定性分析结果. 在该低帧率视频中，由于目标运动缺乏连续性，导致从提议分布位于概率分布的边缘区域，从提议分布采样的有效率极低，因此传统粒子滤波跟踪器在较短的时间内就丢失了目标. MCMCPF跟踪器的跟踪失败则主要是由于在采样初期选择了不恰当的状态转移核，同时陷入了局部最优，在目标运动不连续的情况下，这种情况出现的概率很高. 本文提出算法通过同时构建多条互相独立的马氏链，增大了采样范围，保证了在高置信度区域能够采集足够数量的样本，在目标运动不连续的情况下仍能实现较为准确的跟踪.

4 结 论

提出一种用于物体跟踪的IOMC粒子滤波算法，并通过仿真实验以及真实视频中的实验证明了其性能的优异性.当场景中存在与目标相似的背景区域或者物体时，目标的后验概率分布往往存在多模态.IOMC粒子滤波算法采用延迟判断的策略，首先通过重要性排序同时构建多条独立马氏链，以分别对不同的模态进行充分逼近拟合，然后选择最优模态的峰值作为状态估计值，能够在后验分布呈多模态的复杂背景下实现鲁棒的视频跟踪.在将来的工作中作者将着重研究将本文算法与自适应性以及辨识性较强的物体表征模型结合，以更好地应对跟踪中目标与其他物体交互、遮挡以及场景中光线突变等复杂情况.

[1] Cue H，Cadre J-P L， Perez P. Tracking multiple objects with particle filtering[J]. IEEE Transactions on Aerospace Electronic System， 2002，38(3):791-812.

[2] Kang H，Kim D，Bang S Y. Real-time multiple people tracking using competitive condensation[J]. Pattern Recognition， 2002，38(7):1045-1058.

[3] Okuma K， Taleghan A， Freitas J F G， et al. A boosted particle filter: multitarget detection and tracking[J]. Computer Vision-ECCV, 2004,3021:28-39.

[4] 王法胜，赵清杰.一种用于解决非线性滤波问题的新型粒子滤波算法[J].计算机学报，2008，31(2):346-352.

Wang Fasheng， Zhao Qingjie. A new particle filter for nonlinear filtering problems[J]. Chinese Journal of Computers，2008，31(2):346-352. (in Chinese)

[5] Isard M，Blake A. Condensation-conditional density propagation for visual tracking[J]. International Journal of Computer Vision， 1998，29(1):5-28.

[6] Zhou S K， Chellappa R， Moghaddam B. Visual tracking and recognition using appearance-adaptive models in particle filters[J]. IEEE Transactions on Image Processing， 2004，13(11):1491-1505.

[7] Stasiak L， Pacut A， Gordon N. Particle filters for multi-face detection and tracking with automatic clustering[C]∥Proceedings of IEEE International Workshop on Imaging Systems and Techniques. Krakow: IEEE， 2007:1-6.

[8] Vermaak A，Doucet A，Perez P. Maintaining multi-modality through mixture tracking[C]∥Proceedings of IEEE International Conference on Computer Vision. Washington D C: IEEE Computer Society Press, 2003:1110-1116.

[9] Kotecha， J H， Djuric P M. Gaussian particle filtering[J]. IEEE Transactions on Signal Processing， 2003，51(10):2592-2601.

[10] Rui Y， Chen Y. Better proposal distributions: object tracking using unscented particle filter[C]∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D C: IEEE Computer Society Press， 2001:786-793.

[11] Gillks W， Berzuini C. Following a moving target: Monte Carlo inference for dynamic Bayesian models[J]. Journal of Royal Statistic Society B， 2001，63(1):127-146.

[12] Pei F， Cui P， Chen Y. Adaptive MCMC particle filter for nonlinear and non-Gaussian state estimation[C]∥Proceedings of International Conference on Innovative Computing Information and Control. Washington D C: IEEE Computer Society Press， 2008:494-498.

[13] Maggio E， Cavallaro A. Hybrid particle filter and mean shift tracker with adaptive transition model [C]//Proceeding of IEEE Signal Processing Society International Conference on Acoustics， Speech， and Signal Processing. Philadelphia: IEEE， 2005:221-224.

[14] Geyer Charles J. Introduction to Markov Chain Monte Carlo [M]. [S.l.]: Chapman and Hall/CRC Press， 2011.

[15] Cite Seer X. PETS 2009 benchmark data set.[2009-01-02]. http://www.cvg.rdg.ac.uk/PETS2009/a.html.

(责任编辑：刘芳)

Object Tracking Arithmetic Based on Importance Ordering Monte Carlo Particle Filtering

XU Wei-cun， ZHAO Qing-jie， WANG Yu-xia, ZHAO Liu-jun

(School of Computer Science， Beijing Institute of Technology， Beijing 100081, China)

In order to obtain efficient object tracking under cluttered scenes, a method was proposed based on importance ordering Markov Chain Monte Carlo (MCMC) particle filtering. Firstly, a few authorized initial particles were made use to approximate the true posterior particle distribution. And then the new particles were drawn from the rough approximation with the proposed importance ordering MCMC sampling strategy to build several independent Markov Chains, corresponding one-to-one to the modes of the true posterior distribution, so as to approximate the multimode of the true posterior distribution. According to the current mode distribution, the method could establish several adaptive independent Markov Chains to approximate the posterior distribution of objects under multimode cluttered scenes. An importance ordering strategy was taken to make fully use of the history samples for state transfer decision, to increase the possibility that small weight samples could be selected and to decrease the probability that build process of Markov Chains got in local optimized. Simulation and verity experiment show that the proposed method can achieve stably and exactly object tracking, its performance is better than the standard particle filtering method and the MCMC particle filtering method.

object tracking; importance ordering; Markov Chain Monte Carlo; particle filtering； multiple modes

2013-09-20

国家自然科学基金资助项目(60772063，61175096)

许伟村(1985—)，男，博士生，E-mail:xuwcun@gmail.com.

TP 273

A

1001-0645(2016)01-105-06

10.15918/j.tbit1001-0645.2016.01.019