履带对地面的包络特性研究

朱兴高， 顾亮

(1.北京理工大学 机械与车辆学院，北京 100081； 2.中国航天标准化与产品保证研究院， 北京 100071)



履带对地面的包络特性研究

朱兴高1，2， 顾亮1

(1.北京理工大学 机械与车辆学院，北京 100081； 2.中国航天标准化与产品保证研究院， 北京 100071)

借助于有限元技术和Matlab软件，利用路面功率谱密度函数构造不同空间频率下的正弦路面，建立了履带、负重轮的有限元模型，研究了履带在重力作用下的变形，得到履带对起伏土路、砂石路、戈壁路、铺面路的包络系数、包络效果及功率谱变化情况. 通过研究履带曲线与正弦地面之间的对应关系，得到4种典型路面下履带对地面的滤波函数. 实现了对4种典型路面的滤波分析，可以直接应用到对道路谱进行修改，为整车道路模拟系统直接对负重轮进行道路激励加载提供理论依据.

功率谱密度；履带；包络特性；滤波函数

由于履带车辆行走机构的复杂性，人们在很早就想找到一种可以类似地面频谱式的函数直接作用于负重轮，以研究履带车辆的各种动态特性，但是由于传统理论和方法的局限性，一直未找到好的方法. 随着科学技术的发展和电子计算机的普及，履带对地面包络特性的研究成为履带车辆行业内的一个热点. 履带对地面的包络作用主要是指履带对地面的滤波和载波作用. 履带对地面的包络特性研究涉及到复杂的履带结构、地面地貌及地面-履带之间、履带-负重轮之间的耦合作用关系，传统的理论很难给出精确的解答[1-8]. 本文作者通过有限元分析和Matlab的曲线拟合来研究履带对地面的包络特性.

1 地面和履带及负重轮有限元模型的建立

1.1 地面模型的建立

地面模型的构建包括地面形貌的建立和地面非线性材料数学模型的选择. 地面形貌的建立根据ISO/TC108/SC2N67规定的标准等级确定. 选取起伏路为研究对象，得到起伏路的路面谱为

(1)

式中：n为空间频率，表示每米长度中包含n个波长，m-1；Gq(n)为路面功率谱密度，m2/m-1.

研究履带对地面的包络特性，在路面不平度的功率谱曲线上取有限个点来构造正弦路面，对起伏路路面谱上的任意一点，可以构造正弦路面，表达式为

(2)

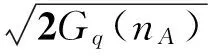
nA=0.1时构造的正弦路面，地面非线性材料数学模型选用修正剑桥模型. 结合正弦路面的地面形貌和地面材料的数学模型，构建的地面有限元模型见图1. 其中，地面模型的单元采用的是6面体单元，单元的长和宽均为100mm，高为400mm. 该模型共有37 088个节点，36 240个6面体单元.

1.2 履带和负重轮模型的建立

履带模型的建立考虑到了履带之间的弹性连接、履带板与地面之间的相互作用关系及履刺效应，故采用了履带的实体结构. 履带单元采用4面体结构，履带模型共有496 900个节点，1 737 800个4面体单元，其有限元模型见图2. 其中，两块履带板之间通过端联器和诱导齿连接，他们的连接方式采用共用履带节点的方式；履带销和履带销孔之间的弹性连接采用不同材料的方式实现.

负重轮的结构考虑了负重轮的挂胶影响，建立的负重轮有限元模型如图3所示. 负重轮的单元采用6面体结构. 由于履带车辆单侧共有负重轮6个，故负重轮的有限元仿真模型共有26 460个节点，23 502个6面体单元.

1.3 负重轮-履带-地面系统模型的建立

前面建立了地面有限元仿真模型、履带和负重轮的有限元模型，结合履带、负重轮及地面之间的相互位置关系及耦合作用关系，建立的负重轮-履带-地面的有限元仿真模型见图4.

负重轮与履带之间、履带与地面之间的耦合作用关系在有限元分析软件中通过设置相应的接触参数来实现.

负重轮-履带-地面系统的外部载荷主要指施加到各负重轮上的动态载荷. 履带车辆在运行过程中，车辆自身的重量载荷不是均匀稳定地分布在每个负重轮上的，而是随着履带车辆的运行工况、负重轮位置及运行时间而发生变化. 就履带对地面的包络特性研究而言，可以假设各个负重轮上分布的动载荷相等，都等于履带车辆的1/12.

负重轮-履带-地面系统的约束主要是指对负重轮的约束和对地面的约束两部分. 首先，履带车辆运行过程中负重轮以一定的速度在履带上滚动，故在负重轮的中心处施加速度约束，速度的大小等于履带车辆的行驶速度，履带车辆运行过程中地面相对静止，故约束地面单元6个方向的自由度.

1.4 有限元计算分析

负重轮-履带-地面系统的地面形貌和地面力学特性复杂，模型规模大，且涉及到材料非线性和几何大变形非线性，有限元模型迭代次数多，计算时间长，为了减少模型计算的工作量，缩短运算时间，研究履带对地面包络特性的初步规律，对模型进行了如下简化，与履带接触的地面为刚性地面，地面模型用二维壳单元表示，简化后的模型见图5.

履带对地面的包络特性首先表现在履带板对地面的改造作用. 为了得出履带仅在重力作用下对地面的包络效果，选取起伏路为研究对象，并选取起伏路空间功率谱曲线上的有限个点来构建正弦路面，利用有限元软件仿真分析履带对正弦路面的贴合程度，计算履带对地面的包络系数，拟合出履带包络后起伏土路的空间功率谱. 仿真计算的条件见表1.

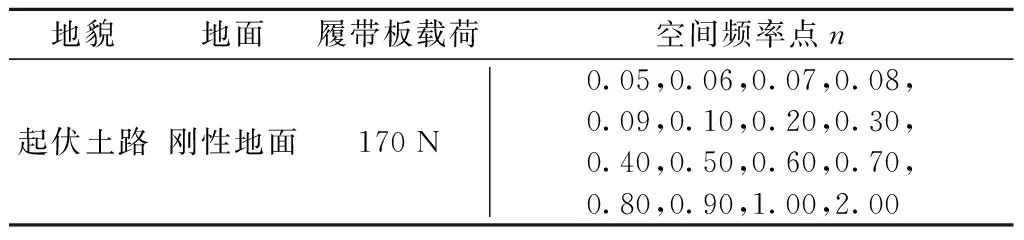
表1 仿真计算条件

有限元仿真分析的边界条件见图6. 其中，地面为刚性地面，约束所有地面节点的6个自由度，每块履带板上的载荷为170 N. 履带变形应力云图见图7，文中只列出了n=0.1的情况.

由图7可知，履带变形后基本与正弦路面贴合，履带的重力克服了两块履带板之间挂胶的扭转阻力，履带的形状与正弦路面基本吻合.

通过对履带变形数据的整理，可以得到履带包络前后地面波形的对比关系如图8.

由图8可知，铺设履带前后的正弦路面，只是幅值发生了改变，而相位和周期都没有明显变化. 对履带包络前后的路面幅值进行统计，得到不同空间频率下履带对起伏土路的包络系数见表2.

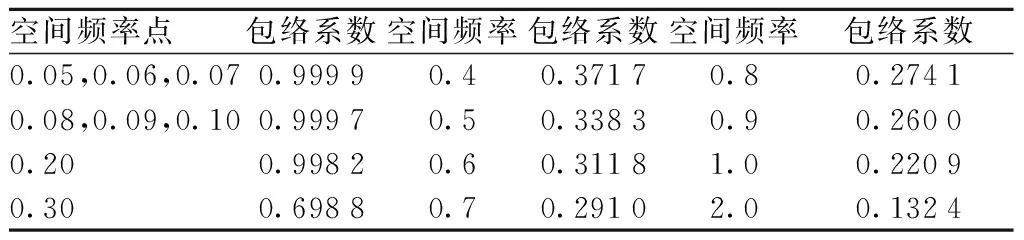
表2 包络系数

1.5 履带对地面的滤波函数

由不同空间频率下的包络系数求得路面不平度系数，进而拟合求出履带包络后的路面功率谱密度函数见表3.

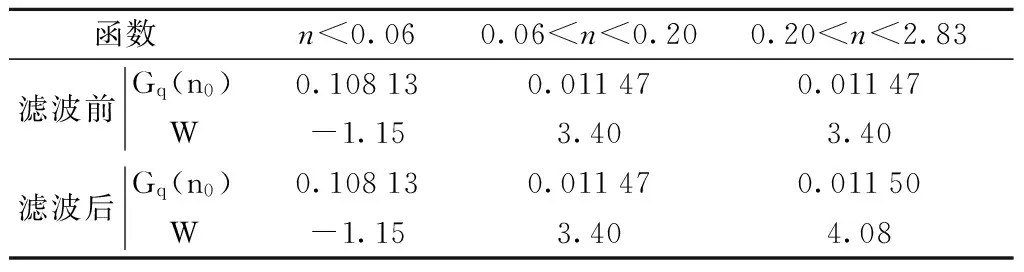
表3 路面功率谱密度变化

表中，n0=0.1 m-1为参考空间频率；Gq(n0)为参考空间频率n0下的路面功率谱密度值，称为路面不平度系数，单位m2/m-1=m3；W为频率指数，为双对数坐标上斜线的斜率，它决定路面功率谱密度的频率结构[8].

履带对地面的包络作用主要表现为履带对路面谱的滤波作用，特别是地面功率谱中的高频成分，履带的滤波作用更加明显. 履带对地面的滤波作用类似于二阶低通滤波器的作用，履带对地面的滤波函数认为是二阶低通滤波器的幅频特性.

二阶低通滤波器的幅频特性标准形式为

(3)

式中：G(ω)为滤波器的幅频特性；ωn为二阶滤波器的固有频率；ξ为二阶滤波器的阻尼系数.

对滤波前后的功率谱密度进行拟合，得到履带对起伏路的滤波函数为

(4)

式中n为路面的空间频率.

采用同样的方法，可以得到履带对铺面路、砂石路和戈壁路的滤波函数为

(5)

2 履带滤波函数的应用

履带车辆进行整车台架试验时，作为路面激励输入应该为去除履带后的路面高程，应用上文研究的滤波函数，对试验测得的4种典型路面(起伏路、铺面路、砂石路和戈壁路)高程进行滤波分析，将滤波后的路面高程作为台架试验的路面激励输入.

通过试验测得4种典型路面高程，在4种典型路面滤波函数的基础上，以起伏土路为例，使用Matlab软件得到起伏土路左右两侧路面滤波前和滤波后的时域对比图和频域对比见图9～图11.

利用相同的方法得到铺面路、砂石路和戈壁路左右两侧滤波前和滤波后的时域和频域对比图，由于篇幅所限不再列出.

3 结束语

利用建立的负重轮-履带-地面系统有限元仿真模型，得到了履带对4种典型路面的滤波函数. 利用构造的滤波函数，对4种典型路面实测的路面高程进行了滤波分析，分析表明，履带对地面滤波作用明显，高程幅值下降，功率谱中的高频成分降低显著，履带对路面谱中高频成分滤波作用明显. 履带滤波函数的构造为整车道路模拟系统激励时，去除履带直接对负重轮进行道路激励加载提供了理论依据.

[1] 钟同才.履带对路面不平度的滤波作用[J].兵工学报(坦克装甲车与发动机分册)，1985(3)：51-58.

Zhong Tongcai. The function of filter track unevenness of pavement[J]. Acta Armamentarii(Section of Tank and Armored Vehicle and Engine)， 1985(3):51-58. (in Chinese)

[2] Auersch L. The excitation of ground vibration by rail traffic: theory of vehicle-track-soil interaction and measurements on high-speed lines[J]. Journal of Sound and Vibration， 2005(284):103-132.

[3] Liu Y, Liu G. Modeling of tracked mobile manipulators with consideration of track-terrain and vehicle-manipulator interactions[J]. Robotics and Autonomous Systems， 2009，57 :1065-1074.

[4] 史力晨，王良曦，张兵志.一类装甲车辆对不平路面的激励响应模型[J].装甲兵工程学院学报，2003(3):43-46.

Shi Lichen， Wang Liangxi， Zhang Bingzhi. Ride dynamic simulation of armored vehicle and experiment validation[J]. Journal of Armored Force Engineering Institute， 2003(3):43-46. (in Chinese)

[5] Ma Zhengdong， Perkins N C. A super-element of track-wheel-terrain interaction for dynamic simulation of tracked vehicles[J]. Multibody System Dynamics， 2006，15(4):347-368.

[6] Wang Weidong. Track-terrain interaction analysis for tracked mobile robot[M]. [S.l.]: IEEE， 2008:126-131.

[7] Javier M. Sobs Raul G. Longoria. Modeling track-terrain interaction for transient robotic vehicle maneuvers[J]. Journal of Terramechanics， 2008，45(3):65-78.

[8] 蒋海波.履带对地面整形作用的研究[D].北京：北京理工大学，2014.

Jiang Haibo. Studying on shaping impact of track on road[D]. Beijing: Beijing Institute of Technology， 2014. (in Chinese)

(责任编辑：孙竹凤)

Research on Envelope Characteristics of the Track on Ground

ZHU Xing-gao1，2， GU Liang1

(1.School of Mechanical Engineering， Beijing Institute of Technology， Beijing 100081， China;2.China Academy of Aerospace Standardization and Product Accurance, Beijing 100071, China)

Applying finite element technology and Matlab, a sine road was studied with different spatial frequencies by use of road power spectral density, and the finite element mode of track and road wheel were built. Investigating the deformation of track with the action of gravity, the state of changes of envelope coefficient, envelope effect and power spectrum in undulation road, gravel road, desert road and paved road was obtained. A filter function of four typical roads was derived according to the relation of track curves and sine road. The filter analysis of the four topical roads can be directly applied to revise the road spectrum and provide a theoretic fundament for the whole vehicle-road simulation system to power the load wheel.

power spectral density; track; envelope characteristic; filter function

2014-10-14

国家部委基金资助项目(1030020220707)

朱兴高(1984—)，男，博士生，E-mail:zhuxinggao2008@126.com.

顾亮(1958—)，男，教授，博士生导师，E-mail:guliang@bit.edu.cn.

U 469.694； TJ 811.92

A

1001-0645(2016)01-0048-05

10.15918/j.tbit1001-0645.2016.01.009