多尺度移不变稀疏编码及其在机械故障诊断中的应用
2016-11-22朱会杰王新晴芮挺李艳峰王东
朱会杰, 王新晴, 芮挺, 李艳峰, 王东
(1.解放军理工大学 野战工程学院, 江苏,南京 210007; 2.总装工程兵科研一所, 江苏,无锡 214035)
多尺度移不变稀疏编码及其在机械故障诊断中的应用
朱会杰1,2, 王新晴1, 芮挺1, 李艳峰1, 王东1
(1.解放军理工大学 野战工程学院, 江苏,南京 210007; 2.总装工程兵科研一所, 江苏,无锡 214035)
提出了一种融合多尺度信息的高效移不变稀疏编码算法,并用于机械故障诊断. 将移不变稀疏编码作为分类器应用于故障诊断,直接对振动信号进行训练和识别,不需要提取特征和预处理. 为进一步提升效果,将不同尺度的移不变稀疏编码分类器融合在一起. 经实验验证,即使在训练样本和测试样本负载不同的情况下,文中方案仍然能够以较高的准确率识别出轴承的故障位置和程度. 与其他方法相比,文中方法的准确率、鲁棒性更高,具有一定的工程应用价值.
移不变稀疏编码;多尺度;故障诊断;字典学习
故障诊断对提高生产效率、经济效益,防止事故发生具有重要意义. 在机械故障诊断中,特征提取与模式识别是核心. 人工选取特征是一件非常费时和困难的工作,往往需要专业知识才能提取较好的特征[1]. 若能让机器直接使用原始振动信号自动学习一个分类器并进行故障诊断,将会大大降低实际操作的难度. 此外,测试样本的负载与训练样本的负载往往是不同的,还要求诊断方法对负载变化具有鲁棒性,给常规方法带来巨大挑战.
为了提高机械故障诊断效果,近几年研究人员尝试了不少新方法. Xu等[1]使用EMD和能量熵来提取特征,之后采用粒子群优化的支持向量机对轴承故障进行诊断. 由于隐马尔可夫模型(hidden Markov models, HMM)对复杂随机序列具有良好的描述能力;Boutros等[2]使用HMM和K-均值算法对机械振动信号进行识别;Zhao等[3]使用补充的集成经验模态分解算法和时间序列算法对振动信号建模,然后使用HMM对机器状态识别. 尽管这些方法都有不错的表现,但仍需要人工提取特征和设计合适的分类器,需要大量的人工工作、专业知识.
近些年来,由压缩感知所发展而来的稀疏编码将信号表示成一组过完备基的稀疏线性组合,通过自学习实现对信号的最简洁表达. 稀疏编码已经成为神经学、信号处理、图像识别等领域的一种基础而且有效的技术[4]. 经Wright等[5]的实验验证,稀疏编码还是一种鲁棒性强、直观性好的模式识别方法. 基于稀疏编码的模式识别可以直接对原始样本进行学习,不需要挑选特征,减轻了操作者的工作量,而且往往能取得更优的结果.
对于时间序列信号,比如机械振动信号、人声、音乐等,每次截取的信号片段中的特征分布位置是随机的,使用常规的稀疏编码算法对同一特征进行学习,需要考虑该特征位于不同位置的情况,如果样本不充足则给学习带来困难[6]. 一些学者通过使用一种移不变稀疏编码(shift invariant sparse coding,SISC)的技术,将信号稀疏地表示成基与系数的卷积,解决了时间序列信号稀疏表示的问题. Liu等[7]首次将SISC应用于机械故障诊断,验证了该方法优于常规算法. 但他的方案还需要设计合适的分类器,而且计算效率和准确率还有提高的空间.
针对此,文中提出了一种多尺度SISC的故障诊断方案. 通过依次对每个基进行优化[8],将复杂的优化问题转化为一个小规模线性方程组,加快了计算. 由生物学和神经学可知,人类在模式识别时综合利用了不同尺度的信息以提高识别准确率和鲁棒性. 受此启发,文中通过提取多尺度的信息,然后使用证据理论(evidential theory,ET)[9]进行信息融合,以期得到更优的故障诊断结果.
1 方法介绍
1.1 SISC简介

(1)
式中:*表示卷积,编码系数xm,k∈P是稀疏的;ε为高斯白噪声;Q 根据最大后验概率估计求取sk最稀疏的表达,评价sk稀疏程度的代价函数为 (2) 然而,SISC中的基可以在整个信号中平移,相对于常规稀疏编码,SISC的系数矩阵增加了一个维度,给求解增加了难度. 许多学者研究了求解SISC的方法,Smith[6]和Blumensath[10]直接基于梯度对基进行更新,Tang等[11]先将信号转化到频域,再利用梯度求解最优的基. 但这些优化算法精度较低,迭代步长难以精确选择. 1.2 高效SISC算法 吸取K-SVD依次更新每个基的思想,文中使用的SISC在字典学习阶段也依次更新各个基,并抽取非零系数项,可以进一步缩小问题规模. 通过转化为一个小规模线性方程组进行求解,加快了收敛速度. 在系数更新阶段,采用了高效的OMP算法,此外,还可以借助于batch-OMP进一步提高计算效率. 下面主要介绍字典更新方法. 在字典更新阶段保持系数不变,仅对基进行更新,由于系数项不参与更新,该稀疏代价函数可以简化为 (3) 式中Ei,k为第k个信号除去第i个基外的所有误差. 由于di*xi,k=xi,k*di,首先仅分析只有第k个信号时的优化问题,相当于求解式(4)的解 (4) (5) 将式(5)简写为Xdi=E,则根据最小二乘法可得di=(XTX)-1(XTE),而矩阵XTX∈Q×Q,从而将问题转化为一个小规模的线性方程组的解. 这一求解过程可以通过Cholesky分解、LU分解等方法直接求取最优值. 1.3 移不变稀疏编码分类器 稀疏编码还是一种鲁棒性强、直观性好的模式识别方法,该方法已经在人脸识别、声音识别中得到了成功的应用.Wright等[5]将分类问题转化为最优稀疏表示问题,首次把稀疏表示分类方法用于人脸识别并取得了良好的效果;Yang等[5]基于字典学习提出了一个更高效更稳健的稀疏识别方法:Metaface方法.Metaface分别对每类样本学习一组字典,从而减少字典规模且降低了噪声干扰.Metaface将所有类别的字典合并为一个大的冗余字典,使用该冗余字典求解测试样本的稀疏编码系数,并求取样本在各个类别的子字典上的重构误差,把与测试样本具有最小误差的子字典的类别作为目标类别. 虽然文中是基于移不变稀疏编码,但仍采用了类似Metaface的思路. 为了不破坏各个子字典构成的空间,没有将子字典进行合并,而是限定稀疏度T0下,依次使用各个子字典对测试样本进行稀疏表示. 当样本的类别与子字典的类别一致时,重构误差应该最小,即将具有最小重构误差的字典类别作为测试样本的类别. 将该分类器称之为移不变稀疏编码分类器(SISCclassification,SISCC). 1.4 融合多尺度的SISCC 实测的机械振动信号常受到大量噪声污染,并且可供训练的样本数量有限,有必要进一步提高稀疏编码的分类能力. 一些学者在字典学习的优化准则中添加了辨别性的限制条件,增大不同类别信号之间的编码分布. 但这导致一些快速的字典学习方法无法使用,大幅增加了计算量. 由精神学和神经学领域的一些研究表明,面对未知对象时,人和其他高等动物会自动提取出目标最有意义的不同尺度的特征,然后把它们组合起来作为识别的依据. 这种融合多尺度特征的思想已在故障诊断上得到了应用,提升了识别效果. 对于振动信号而言,不同长度的基具有不同的物理意义. 当旋转机械中的某个部件发生单点故障时,会引起周期性的冲击振荡. 当基的长度等价于一个冲击衰减时,则该基主要包含单个冲击振荡的特性. 而当基的长度等价于两个冲击衰减时,则基不仅包含单个冲击振荡的特性,还包含冲击周期的相关信息. 文中选择不同长度的基来构造多个不同的SISCC,一组长度相同的基对应于一个分类器,每个分类器都要分别对每类样本单独进行字典学习,得到该类对应的子字典. 定义第q(1≤q≤Q)个SISCC分类器中第l(1≤l≤L)个子字典Dl对测试样本sk的重构率为 (6) 式中:1≤l≤L为类别;L为类别总数. 然后将同一个分类器的所有重构率进行归一化: (7) (8) 从而根据最大概率判断出测试样本的类别. 融合多尺度的SISCC步骤如下. ① 初始化参数. 设定每个SISCC中基的长度hl,每类字典基的个数L和稀疏度T,并将训练样本的能量归一化. ② 字典学习. 针对每个SISCC,按照训练样本的类别依次进行子字典学习,为每类样本学习到一个子字典. ③ 依次使用各个SISCC对测试样本进行识别. 对于第q个SISCC,使用该分类器的L个子字典依次对测试样本进行编码和重构,并将所有重构率进行归一化. 最终得到每个分类器的每个子字典所对应的重构率: ④ 使用证据理论融合Q个分类器的判断,并输出最终判别结果. 2.1 在轴承故障诊断中的应用2.1.1 实验介绍 文中使用西储大学轴承数据,该数据被认为是检验机械故障诊断方法的基准. 使用电火花加工技术分别在轴承外圈(3点钟、6点钟、12点钟方向)、内圈、滚动体上布置了单点故障,故障直径分别为0.007,0.014,0.021,0.028 in(1 in=2.54 cm),每种状态都分别在负载为0,1,2,3 hp(1 hp=746 W)的工况下分别测试,转速分别对应于1 797,1 772,1 750,1 730 r/min. 信号的采样频率为12 kHz. 为了能够同时区分出故障类型和故障程度,将数据分为16类,每一类数据都包含负载为0,1,2,3 hp 4种工况,数据与类别的对应关系见表1. 表1中IR、B与OR分别为内圈、球和外圈故障,其后的数字代表了故障程度,@表示故障点所处方位. 比如,OR007@6表示轴承外圈故障,故障直径为0.007 in,故障点位于6点钟方向. 将每个数据无重叠地分割为长度为2048点的样本,正常状态下的一个数据大约可以分割为118个样本,故障工况的每个数据大约可以分割为59个样本. 表1 数据与类别的对应关系 2.1.2 实验分析 共使用3个尺度的SISCC,3个SISCC中基的长度分别为80、160和240点,稀疏度T分别26、19和15,每个子字典学习15个基. 首先从负载为0 hp的每类数据中随机抽取20个样本作为训练样本,依次使用3个SISCC进行字典学习,每个SISCC学习到16个类别的子字典. 图1为不同状态、不同尺度的部分基的波形,由于篇幅有限,这里仅列出了正常、外圈故障(OR007@6)、内圈故障(IR007)和球故障(B007)4类,同一类同一个尺度仅画出了一个基的波形. 由图1可知,不同状态下基的波形有明显的差异,不同尺度的基也有很大的差异. 尺度1(80点)的基仅包含单个冲击的特性,随着基的长度的增加,还包含了冲击的周期信息,但对单个基刻画的细致程度不如尺度1. 此外还使用尺度2(160点)下的上述4类字典对4类测试样本分别进行了重构,重构的时域波形如图2所示,方框内的信号重构效果最优. 这说明使用相同类别的子字典对测试样本进行重构时,重构效果比较好,也说明了文中方案的合理性. 2.1.3 与其他方法的识别结果对比 Liu[7]使用常规的SISC也分析了相同的数据,他将SISC的系数作为特征输入分类器进行故障识别. 但他使用的测试样本较多,即从负载为0 hp的每类数据中抽取1/2的样本. 文中仅从负载为0 hp的每类数据中抽取20个样本进行训练. 使用多尺度SISCC对0 hp负载下的全部的样本进行识别,结果如图3. 多尺度SISCC能够在稳定负载下准确地识别轴承的故障位置和程度,仅对球故障数据B021的识别有误差,其余全部达到了100%的准确率. 而Liu的方法的稳定性和准确率都较低. 此外,同样在处理器为dual-core 2.2 GHz和内存为 DDR 667 2 G的电脑上实验,Liu的方法对样本训练的时间大约为16 h,而文中方案需要5 h,在效率上有明显的提高. 此外,Zhao[3]曾经使用补充的集成EMD算法和时间序列研究了该数据库中负载为0 hp的数据,但他仅把所有数据分为正常、外圈故障、内圈故障、球故障4类,没有区分故障的程度,平均准确率为97.5%. 而SISCC虽然对故障位置和程度同时进行了识别,但最低准确率都高于Zhao实验中的平均准确率. 可见,文中方案是具有一定优势的. 为了满足实际诊断,还在负载和转速变化的情况下,测试了文中方案的性能. 分别从0 hp和2 hp负载下的每个信号中随机抽取15个样本放入训练集,共有15×16×2=640个样本,然后对所有负载下(0,1,2,3 hp,转速分别为1 797,1 772,1 750,1 730 r/min)共4 379个样本进行测试. 总体上看,多尺度SISCC能够在不同负载及转速下准确地识别出轴承的故障位置和故障程度,满足了实际需求. Dong等[12]也分析了该数据库的相关数据,他使用主成分分析提取信号特征,然后使用Morlet核支持向量机进行分类. 他对数据Normal、IR007、IR014、IR021和IR028进行了识别,在最好的参数下准确率能达到100%,与本实验中对这几个数据的识别准确率一样. 但本实验中同时识别了16类状态,难度更大. 本方案最突出的优势在于可以直接对原始样本进行训练并识别,不需要人工挑选特征,减轻了使用者的工作量,不易受人的主观影响. 为了更全面地评价多尺度SISCC的性能,还使用单一尺度的SISCC做了上面的实验,平均识别结果如图4所示. 可以看出,多尺度SISCC准确率最高. 2.2 在液压泵故障实验中的应用 实验采用的液压泵为25MCY14-1B型轴向柱塞泵,通过采集端盖振动信号对其进行状态识别,共设正常、配流盘磨损、缸体磨损和柱塞松靴4种状态,配流盘是实际磨损的配流盘,缸体故障尺寸为0.5 mm深、0.2 mm宽,松靴间隙约为0.25 mm. 泵转速约为900 r/min,采样频率为10 kHz,柱塞个数为7个,每个样本长度为2 048个点. 由于柱塞一次冲击约相当于95个点,SISCC中基的长度分别选为90、135、180个点,3个尺度的稀疏度分别为25、18、13. 从每类信号中随机选择20个样本作为训练样本,选择100个样本作为测试样本. 实验10次做平均,正常、配流盘磨损、缸体磨损和柱塞松靴4种状态的准确率分别为100.0%,90.25%,93.25%和98.5%. 可见,多尺度SISCC仍然有不错的表现,再次验证了该方案适用于机械故障诊断. 针对机械振动信号的性质,通过选择不同长度的基来构造具有不同物理含义的SISCC,然后使用证据理论融合多尺度的信息以提高诊断鲁棒性和准确率. 经实验验证,融合多尺度的SISCC能够准确地识别出轴承的故障,即使负载发生变化时也依然有比较好的效果. 与其他学者的结果比较来看,文中方案提高了准确率,减少了人工工作量,降低了诊断难度,具有一定的应用价值. [1] Xu H, Chen G. An intelligent fault identification method of rolling bearings based on LSSVM optimized by improved PSO[J]. Mechanical Systems and Signal Processing, 2013,35(1):167-175. [2] Boutros T, Liang M. Detection and diagnosis of bearing and cutting tool faults using hidden markov models[J]. Mechanical Systems and Signal Processing, 2011,25(6):2102-2124. [3] Zhao L, Yu W, Yan R. Rolling bearing fault diagnosis based on CEEMD and time series modeling[J]. Mathematical Problems in Engineering, 2014, 2014: 13. [4] Olshausen B A. Emergence of simple-cell receptive field properties by learning a sparse code for natural images[J]. Nature, 1996,381(6583):607-609. [5] Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. [6] Smith E C, Lewicki M S. Efficient auditory coding[J]. Nature, 2006,439(7079):978-982. [7] Liu H, Liu C, Huang Y. Adaptive feature extraction using sparse coding for machinery fault diagnosis[J]. Mechanical Systems and Signal Processing, 2011,25(2):558-574. [8] Aharon M, Elad M, Bruckstein A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]. Signal Processing, IEEE Transactions on, 2006,54(11):4311-4322. [9] Jousselme A L, Maupin P. Distances in evidence theory: comprehensive survey and generalizations[J]. International Journal of Approximate Reasoning, 2012,53(2):118-145. [10] Blumensath T, Davies M. Sparse and shift-invariant representations of music[J]. Audio, IEEE Transactions on Speech, and Language Processing, 2006,14(1):50-57. [11] Tang H, Chen J, Dong G. Sparse representation based latent components analysis for machinery weak fault detection[J]. Mechanical Systems and Signal Processing, 2014,46(2):373-388. [12] Dong S, Sun D, Tang B, et al. A fault diagnosis method for rotating machinery based on PCA and morlet kernel SVM[J]. Mathematical Problems in Engineering, 2014:8. (责任编辑:孙竹凤) Multi Scale Shift Invariant Sparse Coding for Robust Machinery Diagnosis ZHU Hui-jie1,2, WANG Xin-qing1, RUI Ting1, LI Yan-feng1, WANG Dong1 (1.PLA University of Science and Technology, Nanjing, Jiangsu 210007, China; 2.The First Engineering Scientific Research Institute of General Armaments Department, Wuxi, Jiangsu 214035, China) An efficient shift invariant sparse coding (SISC) algorithm which combined multi scale information was proposed for machinery fault diagnosis. The SISC was applied as a classifier for fault diagnosis, and it could directly train and recognize the vibration signals without feature extraction or pre-processing. What’s more, multi scale SISC classifiers were combined for better performance. Validated by experiments, although the loads of training samples and testing samples were not the same, this scheme could still precisely determine the fault location as well as the severity of fault for bearings. Compared with other methods, the proposed algorithm shows high accuracy , strong robustness and a certain value for engineering application. shift invariant sparse coding; multi scale; fault diagnosis; dictionary learning 2014-09-29 国家自然科学基金资助项目(61472444,61472392) 朱会杰(1987—),男,博士,E-mail:zhuhuijiehao@163.com. 芮挺(1972—),男,副教授,E-mail:rtinguu@sohu.com. TN 165.3 A 1001-0645(2016)01-0019-06 10.15918/j.tbit1001-0645.2016.01.004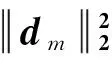
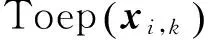

2 融合多尺度的SISCC在机械故障中的应用

3 结束语
