Flight Schedule Recovery under Uncertain Airport Capacity

,

College of Civil Aviation, Nanjing University of Aeronautics and Astronautics,Nanjing 211106, P.R. China



Flight Schedule Recovery under Uncertain Airport Capacity

ZhuBo,ZhuJinfu*

College of Civil Aviation, Nanjing University of Aeronautics and Astronautics,Nanjing 211106, P.R. China

(Received 22 December 2015; revised 12 March 2016; accepted 19 March 2016)

Airlines adjust their flight schedules to satisfy more stringent airport capacity constraints caused by inclement weather or other unexpected disruptions. The problem will be more important and complicated if uncertain disruptions occur in hub airports. A two-stage stochastic programming model was established to deal with the real-time flight schedule recovery and passenger re-accommodation problem. The first-stage model represents the flight re-timing and re-fleeting decision in current time period when capacity information is deterministic, while the second-stage recourse model evaluates the passenger delay given the first-stage solutions when one future scenario is realized. Aiming at the large size of the problem and requirement for quick response, an algorithmic framework combining the sample average approximation and heuristic method was proposed. The computational results indicated of that the proposed method could obtain solutions with around 5% optimal gaps, and the computing time was linearly positive to the sample size.

flight recovery; passenger re-accommodation; two-stage stochastic model; sample average approximation; heuristic method

0 Introduction

In airline daily operations, the flight irregularity is intrinsically inevitable due to dynamic environment. The uncertainty of weather and other events reduce the airport capacity, which leads to airport congestion and incurs flight delay and cancellation. Recovery policies could be implemented to mitigate the disruption. In 2013, the average on-time ratio was 78.4% in the U.S. according to the 16 main carriers′ data from Bureau of transportation statistics(BTS). Each irregular flight costs $16 600 on average, including expenses on fuel, maintenance, crew, passenger time and welfare loss. The situation is nothing but worse in China. According to the official statistic, the number of irregular flights was up to around 769 000, and the average punctuality ratio was only 72.34% in 2013, which meant about 2 100 irregular flights waited for being dealt with every day. With the speedy development of air transportation in China, the disequilibrium between increasing flight demand and the relative stable air transportation capacity is prominent. The airport slot, which is the time allocated for an aircraft to land or take off, has become a scarce resource in recent years[1].

There are two flight network of airlines: City pair and hub-and-spoke. In city pair network, the disruptions on airports are less troublesome because most passengers travel in itineraries without transferring flights. However, in hub-and-spoke flight network, since large-scale of flights are operated and passengers transfer flights in the hub, disruptions may spread to following flights.The slot resources in hub airports, such as Beijing, Shanghai, have already run out for regular operations. When inclement weather or other unexpected events reduce the airport capacity, the aviation authority (such as FAA, CAAC etc.) provides a set of slots for each airline at the disrupted station, and a free flight program allows an airline to assign legs to the set of slots[2].

There are four sub-problems for flight recovery, dealing with the flight timetable, aircraft, crews and passengers. The schedule recovery problem (SRP) is to re-time the flight schedule and determine the cancellation, so it is the basic work for the other three sub-problems. The aircraft recovery problem (ARP) re-assigns aircraft to re-scheduled routings and keeps fleet balance for flights beyond recovery period. The crew recovery problem (CRP) generates new duties for crews. The passenger recovery problem (PRP) re-accommodates disrupted passengers to new itineraries to deliver them to their destinations.

Since aircraft are the most important resources for airlines, ARP attracts most academic focus. Jarrah and Yu researched the network flow model with the aircraft shortage[3]. Yan and Yang studied the flight schedule recovery problem with airport temporary closure[4]. Argüello, Bard and Yu discussed the flight schedule recovery problem with temporary shortage of aircraft, and applied GRASP algorithmic framework to rearrange aircraft routings[5]. In reference to PRP, Bratu and Barnhart studied the flight delay, cancellation decision and the passenger re-assignment, considering the passenger arrival delay cost[6]. Zhang and Hansan researched schedule and passenger recovery for a one-stage hub-and-spoke network, considering both arrival and departure capacity constraints[7]. Bisaillon et al. studied passenger reassignment problem combining fleet assignment and aircraft routings, they designed a large neighborhood search heuristic method to identify improved solution while retaining feasibility[8]. The above references concentrated on individual recovery, regarding aircraft, crews, and passengers separately. Recently, more research emphasizes on integrated recovery. Abdelghany studied integrated decision-making tools for flight recovery problem, and put forward the integrated recovery solution with all flight resources involved[9]. Petersen et al. are known as the first team who the fully integrated recovery formulation and approach with computational results presented[10].

The above assume that disruptions are known before decision-making. However, the significant inherent uncertainties make the recovery problems more complicated. Recovery plans from deterministic model result in lack of robustness and more operational costs. In recent years, stochastic programming shows its advantages in many industries such as transportation, manufacturing, finance, and logistics etc. Although few works have been published on airline stochastic recovery problem, there are some research on other aviation fields. Considering the stochastic scheduling of airlines, Rosenberger et al. worked on the simulation software that controlled the uncertain delay time in airline operations[11]. Wu explored the inherent delays of airline schedules resulting from limited buffer times and stochastic disruption in airline operations, and the results indicated that airline schedules must consider the stochasticity in daily operations[12]. Yen and Birge established a two-stage stochastic integer model on airline crew scheduling problem under uncertain disruptions. They designed a flight-pair branching algorithm[13]. Silverwood[14]and Karacaogˇulu[15]reviewed the application of stochastic programming techniques on airline scheduling. They indicated that stochastic programming techniques were able to improve the delay recovery performance of the schedule. Sölveling studied the stochastic programming methods for scheduling of airport runway operations. He established a two-stage stochastic integer model, and used sample average approximation (SAA) method and Lagrangian decomposition to solve the model. He also proposed an improved stochastic branch and bound algorithm[16]. Referring to the stochastic methods in airlines operational field, Mou and Zhao built an uncertain programming model with chance constraint, and solved it based on classic Hungarian algorithm to deal with the recovery problem under stochastic flight time[17]. Arias et al. proposed a combined methodology using simulation and optimization techniques to cope with the stochastic aircraft recovery problem[18]. Guimarans et al. solved the stochastic aircraft recovery problem using large neighborhood search metaheuristic approach combined with simulation at different stages. The results shows stochastic approach performs better than a deterministic approach[19].

e stochastic recovery

, uncertainties were reflected only in the flight times. However, it is stochastic external factors where irregular flights come from in most cases. We studied the flight recovery problem combining re-timing, re-fleeting and passenger re-accommodation when the hub undergoes stochastic decreasing hub capacity.

1 Problem Statement

The essence target of recovery policies is to re-accommodate passengers as soon as possible when irregularity happens. Every recovery plan should maintain flow balance for every plane, crew, and passenger flow. The basic strategies to recover flights are delay and cancellation. Every flight has its scheduled time of departure(STD) and scheduled time of arrival(STA), denoting the original scheduled times of departure and arrival, respectively. After delay and cancellation applied, every active (not cancelled) flight will have its estimated time of departure(ETD) and estimated time of arrival(ETA), which are estimated times of departure and arrival, respectively. To some minor disruptions, delay might be the intuitive recovery policy, and it may be effective if the delay time is acceptable and will not break the flow balance in the system. However, in many cases, ″only delay″ may not be a good strategy because the delay may propagate in the following flights, and will cause passenger or crew misconnection. Cancellation is a quick response to recover the flight schedule, but it is costly because a bunch of passengers will be re-accommodated or spilled, and it may also break the aircraft or crew connections. Cancelling a flight leg usually requires rerouting the aircraft, crew and passenger flows. Since crews and passengers can fly on other legs or even use other transportation mode, there are many ways to maintain their flow balance. Unfortunately, rerouting the plane is more difficult, and the airline may cancel additional legs on the plane′s route[2]. So when cancellation policy is applied, the controllers usually cancel a flight cycle, which is a sequence of legs that begins and ends at the same airport, to maintain aircraft flow balance at airports.

For aircraft recovery, there are some specific strategies. Aircraft swap or type substitution may be applied to find the possible swap opportunities in the same aircraft type or between other types. Reserved aircraft can be used to solve the disruptions caused by shortage of aircraft, but they are not always stand by for economic concern. Ferry is also a backup but least used strategy, which flies to specific station without passengers in order to perform the following flights.

As mentioned before, when inclement weather or other unexpected events emerge, airlines will get the airport capacity information from air traffic control (ATC) authority in terms of available slots in a unit time period (or time stage if there is no ambiguity). Fig.1 illustrates the capacity information and three time periods involved in the problem. Usually the slot information can just be known for the current time period, such as time period 1 in the figure. For the later time periods, such as time period 2—4, the discrete probability distribution can be introduced to the capacity scenarios.

Disruption time periodT0consists of time stages when capacity is reduced.

Recovery time periodT1is the time period when flight schedule and fleet assignment are rebuilt. Once the fleet is determined, it is trivial to assign specific airplane. The recovery process begins at the very beginning of T1, and all flights that scheduled to departure in T1are adjustable. Beyond recovery time period, the flight schedule should go back to normal status. It means, all flights that scheduled to departure beyond T1should not be delayed nor cancelled, and will be operated by the original aircraft type. It is obviously that the longer T1is, the more adjustable flights are involved, the more possible recovery chances are generated, and the higher the computational complexity will be. The shorter recovery time period forces more usage of cancellation, which guarantees the flight can be recovered to normal quite soon, while it may incur more cost.

Re-accommodation time periodT2is the time period when passengers can be re-accommodated. It can cover the whole day along, and even can be extended to a longer time if serious disruption happens. Theoretically, all the disrupted passengers can be re-accommodated in the future if the T2is long enough, since flights are frequently operated in flight schedule.

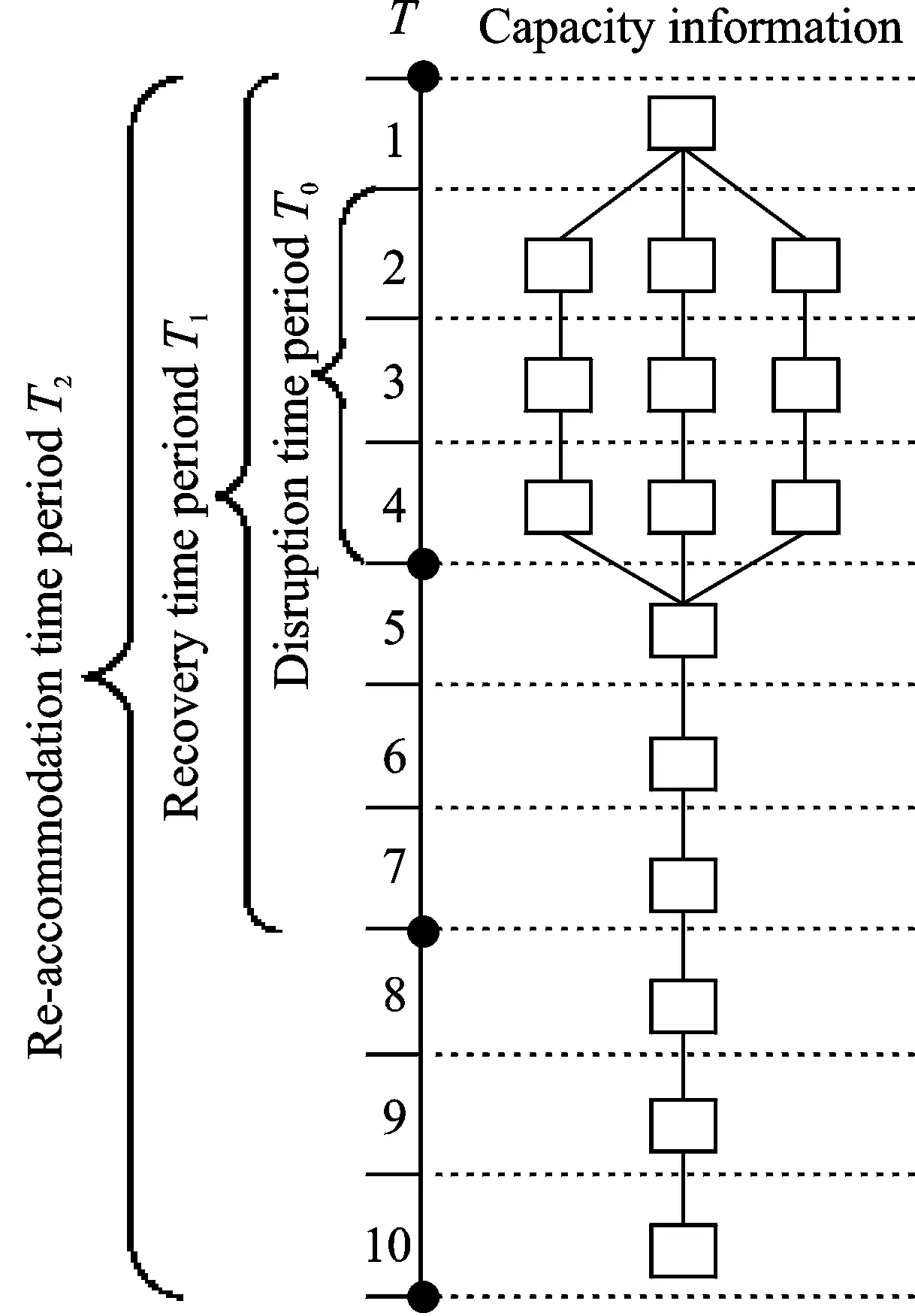
Fig.1 Illustration on time periods involved and capacity information

During T0, the airport capacity is uncertain. In Fig.1, for example, there are three capacity scenarios, each of which has corresponding probability. Solutions should be found for the current time period before one of the scenarios is realized in the future.

Since flight cycles are considered as units in the recovery process, different types of flight cycles are defined in order to distinguish the different roles in recovery process. Fig.2 shows the four types of flight cycles, although all flight cycles simply consist of only two flights in the figure, they can consist more flights in our model.In Fig.2, A,B,C,D,H represent airports. H→B means the flight F11 departs from airport H and arrives at airport B.Notice that the flight cycle confines to the simple cycle without sub-cycle. Cycles of type (1), (2) and (3) are those with STD in the recovery time period, so they are adjustable in the recovery process. The ETA of type (1) is in the recovery time period, so it can be delayed, cancelled or re-fleeted. The last flight such as F22 in type (2) has STD in the recovery time period, so it is suitable to all the recovery policies as well. Notice that although F22 has STA after the recovery period, it might be delayed to some degree, which will be constrained by delay limitation or aircraft balance requirement in the model. Type (3) has flights with STD after recovery period, so in order to guarantee the flights unchanged, the cycles cannot be cancelled, and the fleet type cannot be changed. Since type (3) has flight like F31 which has STD before recovery period, it can be delayed to some degree as long as it does not influence the regular operation of F32. Cycles of type (4) are those with STD after recovery time period, so they are supposed to fly regularly, and cannot be cancelled, delayed or re-fleeted.

Fig.2 Four types of flight cycles

2 Stochastic Model for Real-Time Integrated Recovery Problem

A two-stage stochastic model was established to deal with the flight schedule problem under uncertain reduced capacity in the hub. The classic two-stage stochastic model was proposed by Dantzig[20]and Beale[21]. The first-stage model was designed to find solutions before the uncertain parameters were identified, and the second-stage model presented possible recourse solutions after all the uncertainties were identified. In modeling the recovery problem, assume that the flight network has Naptairports, one of which is the hub airport, where all the involved flight cycles begin and end. The slots resources in the spoke airports are sufficient. It is reasonable because in hub-and-spoke network, the aircraft movements in spoke airports are much lesser than those in the hubs.

2.1 The first-stage model

The first-stage model determines the recovery decisions in the current time stage. Since the flight timetable and aircraft routing are considered simultaneously, there are 4 candidate recovery policies: delay, cancel, fly and fleet re-assignment.

(1) Set and parameters

FC={1,…,fFC}: Set of flight cycles, indexed by i.

FC1: Set of adjustable flight cycles, with STD in current time stage. FC1⊂FC.

F: Set of flight legs, indexed by f.

ε: Set of fleet types, indexed by e.

Ω: Discrete disruption scenario set, indexed by ω.

ae: Number of available aircraft of type e at the hub airport currently.

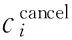
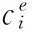
(2) Decision variables

For each flighty cycle i∈FC1,

wi: Cancellation variable, equals 1 if i is cancelled, otherwise 0.

ui: Delay variable, equals 1 if i is delayed to the next time stage, otherwise 0.

vi: Fly variable, equals 1 if i flows in current time stage, otherwise 0.

将上述参数设置之后，将设计的PLC程序重新烧录到PLC中，将组态监控程序烧录到触摸屏中。用MPI电缆将两设备连接，再次通讯，通讯成功触摸屏界面数值显示窗口的数据显示为“00000”。

Let x denote the above decision variables in the first-stage model for expressional simplicity

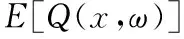
(1)

(2)

(3)

(4)

(5)

2.2 The second-stage resource model

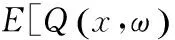
(1) Set and parameters

P: Set of passenger itineraries, indexed by p,r.

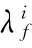
SEATe: Seat number of fleet type e.

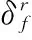
np: Number of passengers on itinerary p.

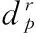
R(p,x,ω): Set of candidate recovery itineraries for each itinerary p based on first-stage decision x under scenario ω, which includes the p itself, the other proper itineraries and a virtual itinerary that models passengers spilled.

(2)Decision variables

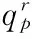
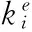
Let y(x,ω) denote the above decision variables in the second-stage model for expressional simplicity.

The recourse model reflects the passenger arrival delay during the entire T1. Notice that not only the fight cycles in the first-stage are considered, but also those re-constructed (combining re-timing and re-fleeting) flight cycles in the future. The objective function of the recourse model is defined

(6)

(7)

(8)

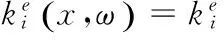
There is an implicited hard work on the recourse model, which is the generation of R(p,x,ω). The generation work is based on the eligible re-constructed flights. Compared with the re-scheduling solutions in the first-stage model, the flight re-construction for the second-stage is much more complicated under one scenario. All the eligible flights must meet the following requirements.

(1) The minimum turn-around time for the consecutive flights in one aircraft routing.

(2) No flight can fly before its STD.

(3) The arrival of flight cycles in each future time stage cannot exceed the corresponding arrival capacity in the hub.

(4) For the flight to fly, an aircraft should be assigned.

(5) At the end ofT1, there are enough aircraft available of each fleet type for the following regular flight schedule.

Theoretically, for each feasible first-stage solution and each scenario, a second-stage resource solutional ways exists since cancellation strategy can always be applied to recover the flights, so the stochastic model has relatively complete resource.

3 Algorithm

The deterministic flight recovery model is already NP-hard, so obviously when it is extended to stochastic problem, more significant computational effort will be required. The proposed two-stage stochastic model has some special features as follow.

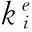
(3) The schedule re-construction solutions for the second-stage model are too large to enumerate even for one given disruption scenario. In our problem, the re-construction solutions in each stage depend on the solutions of the previous stages. As the stage goes further, the solutions number will increase exponentially. Besides, generating a feasible re-constructed flight schedule is time-consuming since the complicated constraints mentioned in the previous section. Thus, the resource model is not easy to solve.

(4) The passenger itinerary recovery work in the resource model can be solved quickly for given x, ω, and the re-constructed flight plan. (The detail algorithm to solve the model will be elaborated later)

For stochastic programs with large solution space of recourse model, a number of sampling based approaches have been proposed.Random sampling methods are used to obtain the statistical estimates of the expected value function. They can be classified into two groups: interior sampling and exterior sampling methods. Sample average approximation (SAA) method is one of the exterior methods where the sampling and optimization are decoupled. The basic idea is quite simple: random samples of scenario are generated and the expected value function is approximated by the corresponding sample average function[22]. More information on the SAA method can be found in Ref. [22]. Due to the requirement of short response time for recovery problem, an algorithmic framework is proposed to combine SAA method and heuristic algorithm, which is referred to the Sölveling′s approach in Ref. [16], to obtain good solutions in tractable computing time. The basic idea of the algorithm is listed as follows, and the details of the key techniques will be described in the following subsections.

(1) Enumerate the feasible decisions on flight cycles in the first-stage model.

(2) Index each first-stage solution as a node within the resulting decision tree.

(3) For each node, evaluate a sample set of candidate paths originating at the node viarandom sampling.

(4) Solve the corresponding SAA problem to obtain the upper bound for each node.

(5) Heuristically compute the lower bound for each node.

(6) Prune the nodes that are not promising.

3.1 Upper bound estimation

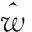
(9)

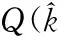
(10)

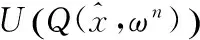
(11)

3.2 Passenger itinerary recovery algorithm

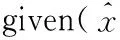
In each stage, the passenger itineraries are ordered by their ″value″,which was defined as how much they paid on their itineraries. High-value passengers will have higher priority in re-accommodation process. Since passengers are clustered in different itineraries in the paper, the disrupted passengers in highest priority itinerary will be re-accommodated first to the least delayed available itinerary. The algorithm can always obtain satisfactory solution because spilled passengers can transferred to the virtual itineraries. This greedy process will perform continuously until all passengers confirmed their new itineraries, and the delay cost is trivial to compute then. The detail of the passenger itineraries recovery algorithm is listed as follow.

Sort the set F in according with the ascending STD

forfinthe sorted set ofF

search to find the involved itineraries and generate a value-descending itinerary set Pf

forp∈Pf

generate R(p,x,ω) and sort it according to the ascending ETA

while the number of passengers who has not been re-accommodated nbp>0 do

if R(p,x,ω) cannot find available seats except for virtual cancellation ones

updatenbp=0

else

greedily transfer the passengers of itinerary p to the R(p,x,ω)

end while

end for

end for

3.3 Lower bound estimation

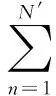
(12)

is defined as the SAA problem and can be solved as a deterministic optimization algorithm. The SAA method proceeds by solving the SAA problem as Eq.(12) repeatedly. By generating M independent samples, each of them with size N′, and solving the associated SAA problems, one can obtain objective values Z1N′,Z2N′,…,ZMN′. Let

(13)

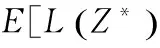
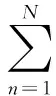
(14)

where j represents the index of sampling from re-construction solutions. When j→,

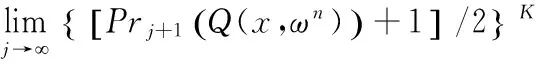
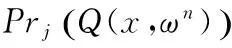
3.4 Termination criteria

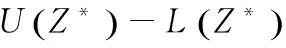
4 Computation

A small case was generated based on the operational data from a Chinese airline. The flight network held 6 airports (Napt=6), which consisted of 5 spoke airports and one hub airport. There were 47 flight legs, which compose 23 flight cycles, operated by 9 aircraft of 2 types (with MTT 40 and 60 min, and seat capacity of 200 and 250, respectively) in this case. 7 797 passengers who were grouped in 82 itineraries traveled in the flight schedule network from 08:00 to 02:00 in the next day. T0was defined as 09:00—13:00, T108:00—18:00, and T208:00—02:00 in the next day. If some passengers couldnot be re-accommodated during T2, they would be re-directed to the virtual spilled itinerary. The other relative parameters and their values are listed in Table 1. The algorithmic framework was implemented in C++ and Python on a laptop with 4 GB installed RAM and i5-3317U CPU 1.70 GHz.

For the first-stage, the capacity of the hub was known. Three disruption scenarios were simulated to represent minor, medium, severe weather conditions which would reduce the hub capacity by 25%, 50% and 75%, respectively. To compare different weather conditions, different probabilities on the three conditions were set to generate different sets ΩAand ΩBas shown in Table 2.

Table 1 Parameters in the small test instance

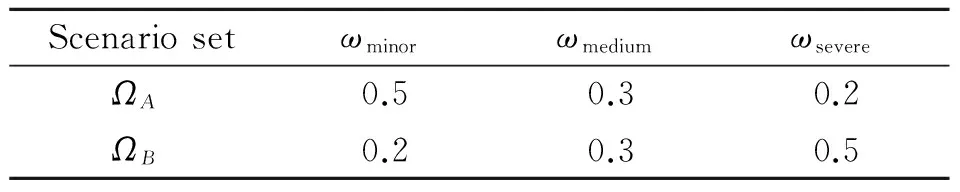
Table 2 Probability of scenario set

The first-stage model has 3 solutions (represented by x1, x2, x3), and the second-stage model will be used to evaluate the influence of those solutions under stochastic disruptions. Table 3 lists the computational results of the two different scenario sets. LB, UB, and OG represent lower bound, upper bound, and optimal gap, respectively. Since ΩAhad a more positive weather condition forecast than ΩB, the objective values of their three solutions exhibited much lesser cost than the counterparts of the latter ones. The optimal gap for each solution was around 5%, which was good enough for operational problems. The two problems both chose first-stage solution x1, which indicated that under such two different uncertainty scenario sets, the performances of x1were both promising. It was reasonable because x1represented the decision with least deviation of the original schedule.

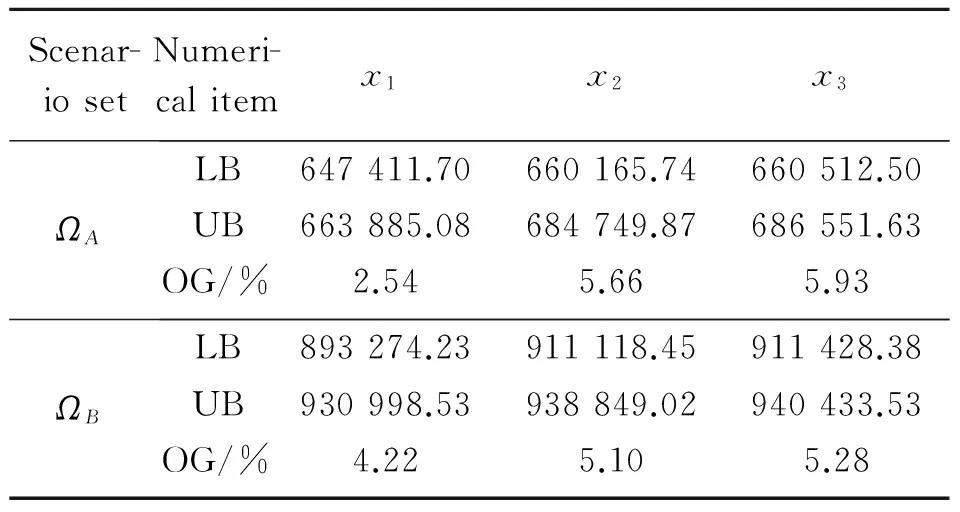
Table 3 Computational results for the small case

To study the computing time of the algorithm, different values of sample size N were set to test the case under ΩA. Fig.3 shows the average CPU times for the problem with sample size N∈{200,400,…,2 000}. It indicates that the computing time is almost linear to the sample size. As long as the computing time is shorter than the unit time period, the recovery process can be conducted dynamically to accommodate airlines daily operation under stochastic circumstances.

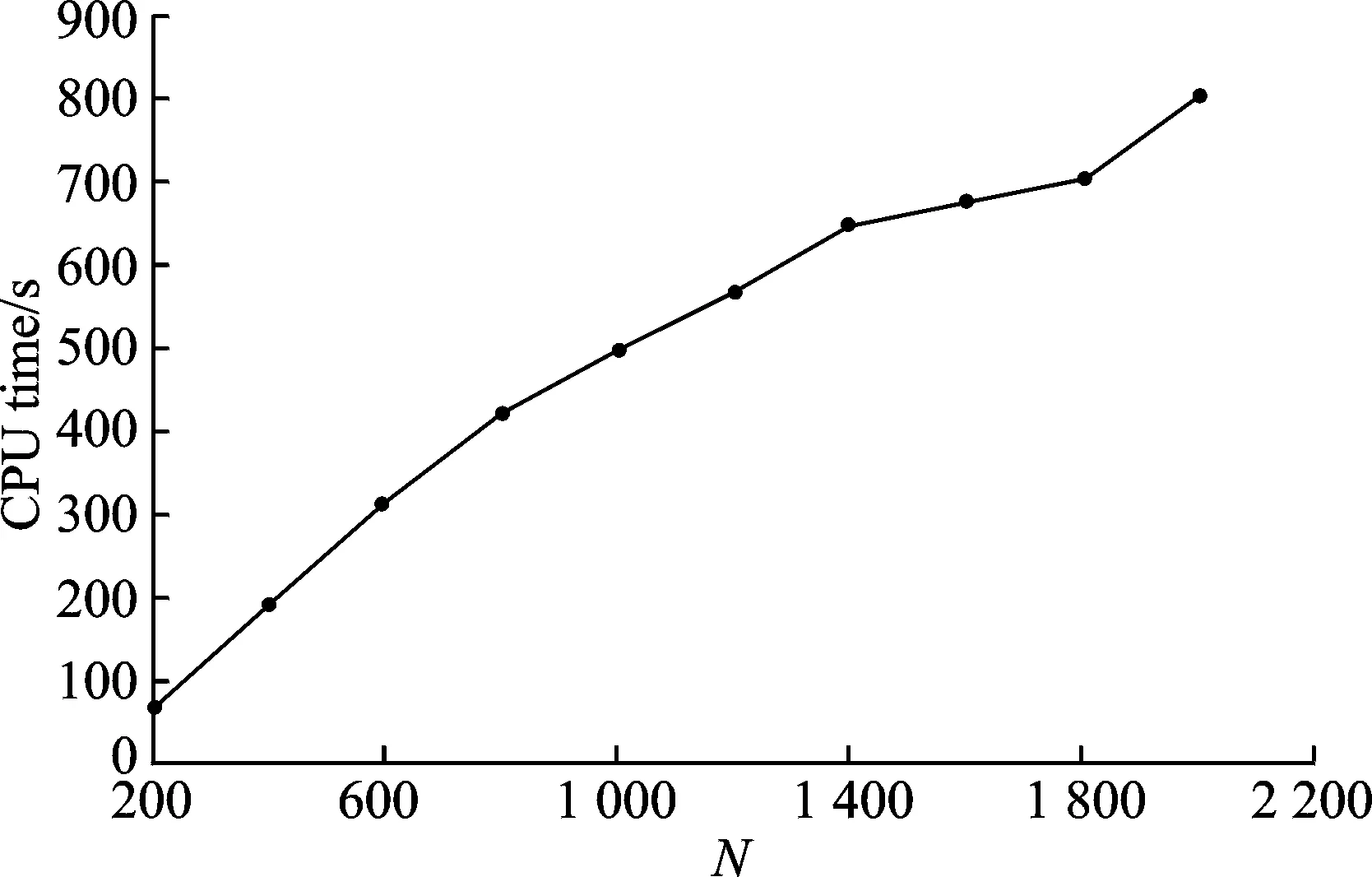
Fig.3 Average CPU times for different N

Fig.4 Upper bound, lower bound, and optimal gap for different N

Fig.4 shows the upperbounds, lower bounds, and optimal gaps for different sample sizes range from 200 to 2 000. Figs.4 (a,b) show that the upper bounds and lower bounds will decrease monotonously when N increases, which indicats that better solutions will be obtained with larger N. Fig.4 (c) shows the optimal gap also has the decreasing trend although there are some outliers due to the stochasticity. Considering the CPU time performance showed in Fig.3, it is obvious that there is trade-off between computing time and the solution quality. Decision makers can choose appropriate sample size based on the available response time when irregularity happens.

5 Conclusions

In this paper, flight recovery problem combining flight timetable, fleet re-assignment and passenger re-accommodation under uncertain hub capacity was studied. It was modeled as a flight cycle oriented two-stage integer stochastic problem. Since the model had some special structure features, an algorithmic framework based on sample average approximation and greedy heuristic methods was designed. The case from a Chinese airline was chosen to test the method. The results showed that for a small sample size, the optimal gap was around 5%, which satisfied operational problems. The computing times were also tracked and they were linear to the sample size. Thus, the proposed method showed its ability of obtaining satisfying solution in tractable time.

There are some interesting problems raised for future work during the research. Theoretically, if parallel computing technique is used, every first-stage model solution can be sent to different CPUs, and with high-speed computer, the computing time can be controlled to be shorter than a smaller time period, like 5 min. This requires large scales of tests to calibrate and evaluate. The disruption scenario set is assumed to be finite in this paper, and this situation can be extended into a scenario tree to represent more precise stochastic information on the disruption.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos.61079014, 71171111), the Funding of Outstanding Doctoral Dissertation in Nanjing University of Aeronautics and Astronautics (No.BCXJ13-14), and the Funding of Jiangsu Innovation Program for Graduate Education (No.CXZZ13_0174).

References:

[1] ABEYRATNE R I R. Management of airport congestion through slot allocation[J]. Journal of Air Transport Management, 2000, 6 (1): 29-41.

[2] ROSENBERGER J M. Topics in airline operations[D]. Atlanta, USA: Georgia Institute of Technology, 2001.

[3] JARRAH A I Z, YU G, KRISHNAMURTHY N, et al. A decision support framework for airline flight cancellations and delays[J]. Transportation Science, 1993, 27 (3): 266-280.

[4] YAN S, YANG D H. A decision support framework for handling schedule perturbation[J].Transportation Research B: Methodological, 1996, 30 (6): 405-419.

[5] ARGÜELLO M F, BARD J F, YU G. A grasp for aircraft routing in response to groundings and delays[J]. Journal of Combinatorial Optimization, 1997, 1 (3): 211-228.

[6] BRATU S, BARNHART C. Flight operations recovery: New approaches considering passenger recovery[J]. Journal of Scheduling, 2006, 9 (3): 279-298.

[7] ZHANG Y, HANSEN M. Real-time intermodal substitution: Strategy for airline recovery from schedule perturbation and for mitigation of airport congestion[J]. Journal of the Transportation Research Board, 2008, 2052: 90-99.

[8] BISAILLON S, CORDEAU J F, LAPORTE G, et al. A large neighbourhood search heuristic for the aircraft and passenger recovery problem[J]. 4OR, 2011, 9 (2): 139-157.

[9] ABDELGHANY K, ABDELGHANY A, EKOLLU G. An integrated decision support tool for airlines schedule recovery during irregular operations[J]. European Journal of Operational Research, 2008, 185 (2): 825-848.

[10]PETERSEN J D, SÖLVELING G, CLARKE J P, et al. An optimization approach to airline integrated recovery[J]. Transportation Science, 2012, 46 (4): 482-500.

[11]ROSENBERGER J M, SCHAEFER A J, GOLDSMAN D, et al. A stochastic model of airline operations[J]. Transportation Science, 2002, 36 (4): 357-377.

[12]Wu C L. Inherent delays and operational reliability of airline schedules[J]. Journal of Air Transport Management, 2005, 11 (4): 273-282.

[13]YEN J W, BIRGE J R. A stochastic programming approach to the airline crew scheduling problem[J]. Transportation Science, 2006, 40 (1): 3-14.

[14]SILVERWOOD M W. Application of stochastic programming techniques to airline scheduling[D]. Johannesburg, South Africa: University of the Witwatersrand, 2011.

[15]KARACAOGˇULU N. An application of stochastic programming on robust airline scheduling[D]. Ankara, Turkey: Bilkent University, 2014.

[16]SÖLVELING G. Stochastic programming methods for scheduling of airport runway operations under uncertainty[D]. Atlanta, USA: Georgia Technology of Institute, 2012.

[17]MOU D Y, ZHAO W L. An irregular flight scheduling model and algorithm under the uncertainty theory[EB/OL]. (2013-09-01)[2015-07-18].http://dx.doi.org/10.1155/2013/361926.

[18]ARIAS P, GUIMARANS D, MOTA M M, et al. A methodology combining optimization and simulation for real applications of the stochastic aircraft recovery problem[C]// Proceedings of the 2013 8th EUROSIM Congress on Modeling and Simulation. Cardiff, Wales: IEEE, 2013: 265-270.

[19]GUIMARANS D, ARIAS P, MOTA M M. Large neighbourhood search and simulation for disruption management in the airline industry[M]//Applied Simulation and Optimization.[S.l.]:Springer International Publishing, 2015: 169-201.

[20]DANTZIG G B. Linear programming under uncertainty[J]. Management Science, 1955(1): 197-206.

[21]BEALE E M L. On minimizing a convex function subject to linear inequalities[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1955, 17 (2): 173-184.

[22]KLEYWEGT A J, SHAPIRO A, HOMEN-DE-MELLO T. The sample average approximation method for stochastic discrete optimization[J]. Society for Industrial and Applied Mathematics, 2002, 12(2): 479-502.

[23]ZHU B, CLARKE J P, ZHU J F. Real-time integrated flight schedule recovery problem using sampling-based approach[J]. Journal of Computational and Theoretical Nanoscience, 2016, 13(4): 1-10.

[24]MAK W K, MORTON D P, Wood R K. Monte Carlo bounding techniques for determining solution quality in stochastic programs[J]. Operations Research Letters, 1999, 24: 47-56.

Ms. Zhu Bo is currently a Ph.D. candidate in Nanjing University of Aeronautics and Astronautics, who is working on the research of airline management and operations.

Prof. Zhu Jinfu is currently a Professor in College of Civil Aviation of Nanjing University of Aeronautics and Astronautics, whose research interests are transportation management and planning

(Executive Editor: Zhang Bei)

V351.11 Document code: A Article ID: 1005-1120(2016)04-0479-12

*Corresponding author, E-mail address:zhujf@nuaa.edu.cn.

How to cite this article: Zhu Bo, Zhu Jinfu. Flight schedule recovery under uncertain airport capacity[J]. Trans. Nanjing Univ. Aero. Astro., 2016, 33(4):479-490.

http://dx.doi.org/10.16356/j.1005-1120.2016.04.479