A Test Method for the Static/Moving State of Targets Applied to Airport Surface Surveillance MLAT System

,,,,

1. The Second Research Institute of Civil Aviation Administration of China, Chengdu 610041, P.R.China;2. College of Electronic Engineering, University of Electronic Science and Technology of China,Chengdu 611731, P.R.China



A Test Method for the Static/Moving State of Targets Applied to Airport Surface Surveillance MLAT System

HuangRongshun1,PengWe2*,LiJing1,WuHonggang1,LiXingbo1

1. The Second Research Institute of Civil Aviation Administration of China, Chengdu 610041, P.R.China;2. College of Electronic Engineering, University of Electronic Science and Technology of China,Chengdu 611731, P.R.China

(Received 4 November 2015; revised 24 March 2016; accepted 25 April 2016)

Due to the particularity of its location algorithm, there are some unique difficulties and features regarding the test of target motion states of multilateration (MLAT) system for airport surface surveillance. This paper proposed a test method applicable for the airport surface surveillance MLAT system, which can effectively determine whether the target is static or moving at a certain speed. Via a normalized test statistic designed in the sliding data window, the proposed method not only eliminates the impact of geometry Dilution of precision (GDOP) effectively, but also transforms the test of different motion states into the test of different probability density functions. Meanwhile, by adjusting the size of the sliding window, it can fulfill different test performance requirements. The method was developed through strict theoretical extrapolation and performance analysis, and simulations results verified its correctness and effectiveness.

multilateration(MLAT); hypothesis testing; motion state detection; sliding window; geometric Dilution of precision (GDOP)

0 Introduction

Multilateration(MLAT) is a novel positioning technology, and the fundamental principle is to identify locations using time difference of arrival (TDOA)[1]. MLAT system is featured with high positioning accuracy, strong anti-interference capability and good redundancy, which is a basic component of the next generation airport surface surveillance system proposed by International Civil Aviation Organization (ICAO)[2-3].

Airport surface surveillance refers to the process of detecting, positioning, correlating and tracking aircraft and service vehicles in civil airports. The localization signal of airport surface surveillance system based on MLAT technology may come from the transponder and automatic broadcasting signal of aircraft and vehicles[4]. When designing a complete airport surface surveillance system, it not only requires to accurately determine the positions of aircraft and vehicles, but also to detect and determine their motion states, for instance, whether the target is static or moving at a certain speed[5-6].

Detecting target motion state is ultimately a decision-making process or a hypothetic testing problem[7]. Traditional test methods of motion states construct the test statistics according to the target moving model and noise characteristics, then compare the statistics value with selected thresholds, and thus determine the motion state of targets. In general, noise is considered as stable white Gaussian noise, which also coincides with many practical conditions[8-9].

MLAT location algorithm is based on TDOA, which means the related localization equation is nonlinear. Many processing techniques have been proposed with different complexity and restrictions. Linearizing the nonlinear equation by Taylor-series expansion and then solving iteratively is one possible way[10]. Chan adopted two liner approximate equations and the corresponding weighted least squares method to estimate target position. Thanks to its linear closed-form solution, Chan algorithm has been widely used in practical engineering[11]. In 2006, Chan proposed approximate maximum likelihood (AML) method, which can attain the theoretical lower bound, but is unable to fulfill the requirements of practical engineering due to its complex calculations[12]. Huang analyzed the influence of target height difference on three stations positioning accuracy[13]. Sharp and Hahn proposed location method of a three-station with auxiliary height difference. However, this method can only be applied when the geometric relationship between the satellite and the Earth is special[14-15]. A novel method is proposed by Yang et al. that uses known pressure altitudes to improve positioning accuracy in MLAT. But there is no in-depth analysis of the theoretical positioning accuracy and robustness of the method[16].

Due to the particularity of MLAT location algorithm, the errors of estimated target position are related to TDOA measurement accuracy, layout of receiving stations, as well as the relative geometric positions between the target and the set of receiving stations, meaning the location noise of MLAT is related to multiple error variables[17-18]. The application of traditional detection algorithms of target motion state may lead to the degradation of detection performance and even to the failure. Regarding this problem, there is little research at home and abroad and no effective solutions. Yuan and Chen propose a detection algorithm of static state using the features of positioning error and ant colony algorithm[19]. However, this algorithm is rather complex and the calculation is heavy, which therefore is not suitable for the implementation of engineering applications.

This paper proposed a detection method of motion states of airport surface targets based on MLAT systems. The detection method combines the characteristics of MLAT location algorithm, and implements the detection through the designed normalized test statistic within a sliding data window. The proposed method works on the principle that when the target remains static or moving, the normalized test statistic obeys different distributions (central Chi square or non-central Chi square distribution). Through normalization and adjusting the size of sliding window, the proposed method not only eliminates the effects of geometry dilution of precision (GDOP) on detection performance, but also is able to fulfill different detection requirements.

The context of this paper is organized as below: Section 1 is introduction, and Section 2 describes the detailed derivation and performance analysis of the proposed method. Section 3 provides the details of simulation verification. Finally, we draw the conclusion.

1 Theoretical Derivation and Performance Analysis

In the following derivation process, we first presented the formula of static/moving state based on binary hypothesis test, and used the data within a sliding window to implement linear transformation in order to develop a normalized test statistic. The goal is to eliminate the effects of GDOP, and to transform the test of target motion state into the test of the probability density functions.

1.1 Motion state test based on binary hypothesis test

Based on binary hypothesis test, the formula in terms of a target motion state(static/moving) can be represented as

(1)

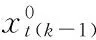
In the following processes, we will define a sliding window consisting ofNposition samples of a target(the positions ofNsamples is estimated by MLAT system ), and use theNth sample(xN,yN) to subtract the rest samples (xi,yi), respectively (i=1，…，N-1), thus we can obtain the differencedxNi，dyNi(i=1，…，N-1) corresponding tox,yaxis

(2)

When the target remain static, namelyvxk=vyk=0 in Eq. (1), then the concrete form of Eq.(2) is

(3)

Here we construct difference vector dwx=[dxN1,dxN2,…，dxNN-1]T,dwy=[dyN1,dyN2,…，dyNN-1]Tforxaxis andyaxis withN-1 values in Eq.(3)， respectively, and where [·]Trepresents transposition.

Therefore， we can use vector dwxto construct the test statistics in order to perform motion test onxaxis (without losing the generality, the procedure and conclusion of dwyis similar to dwx). The specific steps for deciding whether a target is static or moving are as follows:

Step 1 Derive the covariance matrix of dwxbased on MLAT location algorithm characteristic when the target is static.

Step 2 dxyis normalized using the covariance matrix, and to obtain appropriate test statistics.

Step 3 Obtain the detection thresholdMxξaccording to the distribution of test statistics and performance requirement.

Step 4 Determine the motion state of the target using the test statistic and properly chosen threshold in step 2 and 3.

The detailed descriptions of those steps above is as follow. When the state of target isH0(namely the state of target is static), the covariance matrix of dwxcould be expressed as follows according to Eq.(3).

(4)

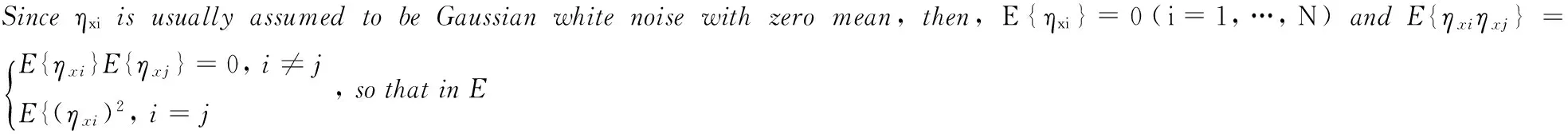
(5)

According to Chan and Sharp[12,14], E{(ηxi)2},i=1,…,NinEq.(5)notonlyrelatestoreceiverthermalnoise,butalsototherelativepositionsbetweentargetandstations,andtherelationshipbetweenthemis

(6)

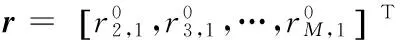
Gt=

(7)

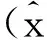
(8)

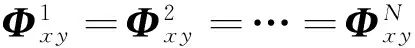
(9)

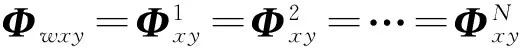
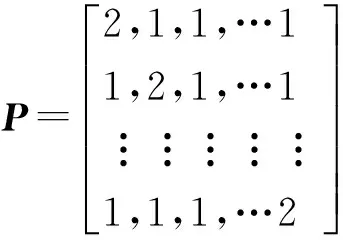
To deal withdwxthrough normalization processing as follows, the influence on test process caused by relative localization geometry between target and stations can be eliminated. Then normalized statistic quantityξxkfor test process can be gotten

(10)

Substitut Eq.(9) into Eq.(10) gives

(11)

1.2 Motion state test based on probability density function

By properly choosing the level of confidence, the threshold valueMxξcan be determined, and hypothesis testing for static or moving target could be made as

(12)

In conclusion, the concrete steps of the test method proposed in this paper applied to judge whether a target is static or moving state are as follows:

(1) Determine the sliding window size Naccordingtoperformancerequirements,anddeterminethresholdMxξandMyξaccordingtolevelofconfidence.Calculatedwxanddwyinslidingwindow,respectively.

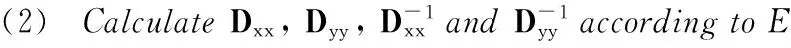
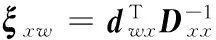
(4)Tomakerepetitivejudgmentaccordingtothestepsdescribedaboveasthenextsampleslidesintothewindow.

2 Simulation

Simulationwascarriedouttoverifythevalidityoftheproposedmethod.Chanalgorithmwasappliedtosimulationtoestimatethetargetlocation.Therewere8stationsandthe(x, y, z)coordinatesofeachstationwere(-114.199 28, 2 913.697 04, -3.489 79), (-331.837 08, -240.138 36, -5.383 16), (586.891 45, 1 854.460 46, 28.302 10),(683.941 72, 3 116.517 55, 18.578 23),(556.024 14, 1 166.376 65, -4.601 39), (-331.926 47, 422.073 61, -4.512 67),(0, 0, 0),and(-0.098 85, 3 527.896 14, -5.710 45) (thesecoordinatesalsoaretheactualstationcoordinatesofMLATatGuilinLiangjiangInternationalAirport).Thetargetcoordinateswas(-360， 300， -10),thetimeintervalofsampleswas1s,theTOAnoisewassetasGaussianwhitenoisewithstandarddeviation3ns.TheexperimentalPDFscamefrom10 000independentMonteCarlotrials.

ThesimulationgeneratedthePDFswhenthetargetwasstaticormovingatacertainspeed,inordertovalidatethecorrectnessoftheproposedmethod,aswellastoassessitsperformance.Thesimulationconsistedofthefollowingtwoparts:

(1)BycomparingthedegreeofcoincidenceofsimulatedPDFsandtheoreticalPDFs(instaticstate),weverifedthecorrectnessoftheoryanalysis;

2)WegeneratdthePDFswhenthetargetwasstaticandmovingatdifferentspeedsandindifferentsizesofslidingwindow.ThePDFwhentargetremainedstaticwasoverlappedwiththosewhentargetmovedatdifferentspeedwithdifferentslidingwindowsize.Thecomparisonsoftheoverlapsshowedtheeffectsoftargetspeedandwindowsizeontestperformancewhichcouldbequantitativelyassessed(sincefalsedetectingandleakingdetectingprobabilitieswererelatedtotheoverlapextentofthePDFs).

2.1ComparisonofsimulatedandtheoreticalPDFs

Fig.1showsthetheoreticalandsimulatedvaluesofPDFswhentargetwasstaticandthesizesofslidingwindowwere3, 5and7，respectively(inthatcasethetheoreticalPDFswerecentralχ2PDFswith2, 4, 6degreesoffreedom).AsshownintheFig.1,thesimulatedresultsfitwellwiththetheoreticalvalues.Itprovesthecorrectnessofpreviousderivation.

Fig.1 Simulated and theoretical PDFs in different sizes of sliding window (target is static)

2.2 Performance Comparisons

LetPfddenotes the probability of false detection, i.e., when target is moving but is determined to be static. LetPlddenotes the probability of leaking detection; i.e., when target is static but the decision is moving. To improve the test performance (i.e. reducePfdandPldat the same time), it requires the overlapping area of the PDF for static target and the PDFs for moving target to be as small as possible.

We simulated the PDFs, when the target was static and moving at different velocities and in different sizes of sliding window, in order to assess the effects of target speed and window size on test performance.

The selected parameters in the simulation were as follows:

(1) The size of sliding window was 3, and the velocity of target was 0.5 m/s, 1 m/s, and 1.3 m/s, respectively.

(2) The size of sliding window was 5, and the velocity of target was 0.5 m/s, 0.6 m/s, and 1.0 m/s, respectively.

(3) Both significance level and false detection probabilityPfdwere set as 0.05.

Figs.2,3 show the simulation results Asxaxis was similar toyaxis, onlyxaxis was simulated.

From above analysis we can see that, with the static target and window size of 3, the distribution of test statistics was centralized χ2distribution with 2 degrees of freedom. In that case the corresponding detection threshold was obtained to be 6 (namelyMxξ=6) from the distribution. In Fig. 2, when the target velocity was 0.5 m/s，1 m/s and 1.3 m/s, the corresponding PDF was non-centralisedχ2distribution (2 degrees of freedom). By calculation, the simulated non-central Chi-square areas to the left ofMxξwere 0.693, 0.145, 0.023 successively when the target velocity values were 0.5 m/s, 1m/s and 1.3 m/s, respectively (namely correspondingPfdwere 0.693, 0.145, 0.023, respectively). Obviously, it indicates that only when the target is moving at 1.3 m/s and the size of sliding window is 3, the proposed method is able to fulfill the performance requirements ofPfd.

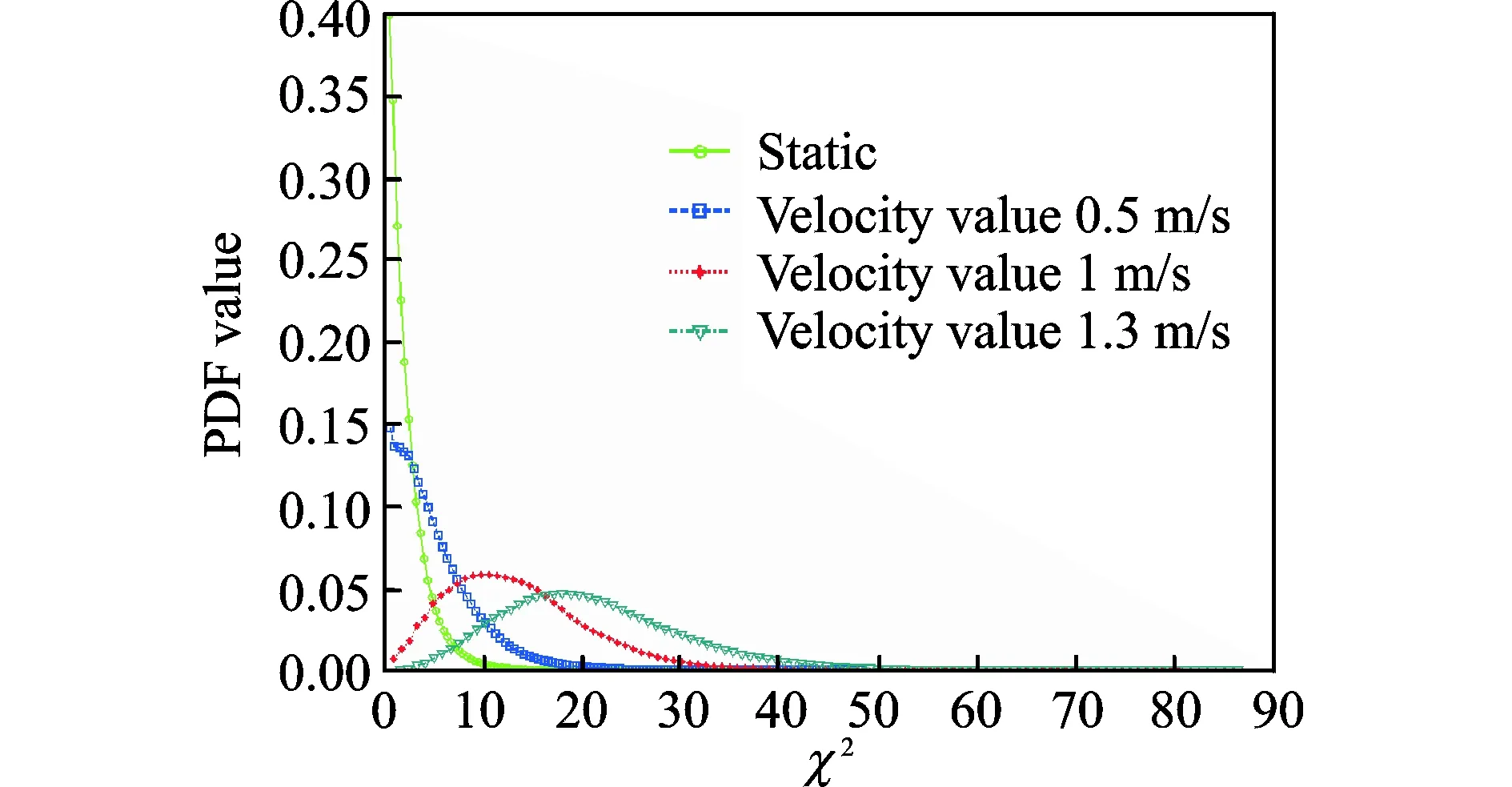
Fig.2 PDFs with different speed when the size of sliding window is 3

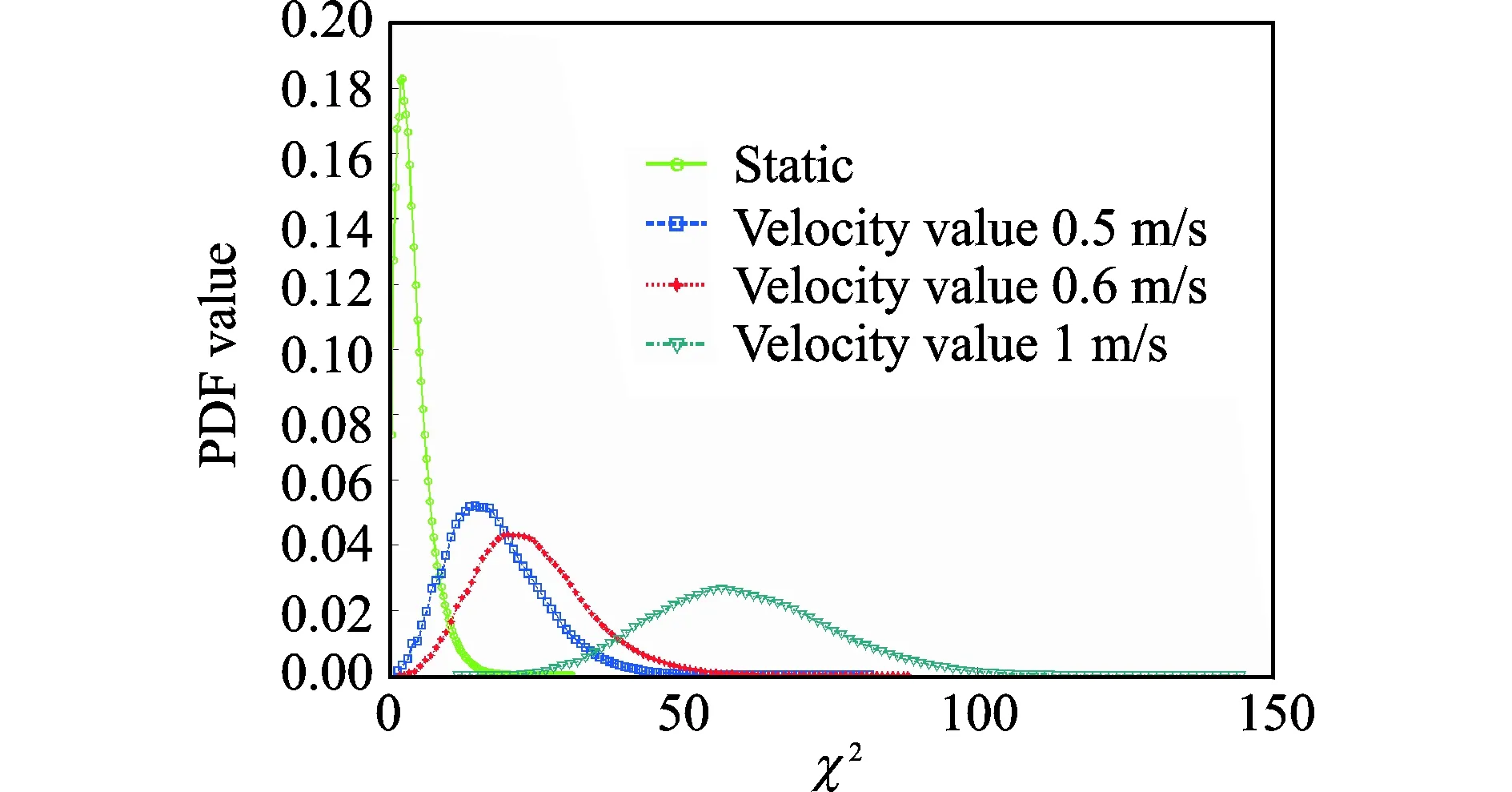
Fig.3 PDFs with different speed when the size of sliding window is 5

With the static target and window size of 5, the distribution of test statistics was centralizedχ2distribution with 4 degrees of freedom. In the same way above, we obtained detection threshold (Mxξ=9.49). The data in Fig.3 indicate that, when the velocity of target was 0.5 m/s, 0.6 m/s and 1 m/s, the simulated non-centralizedχ2distribution (4 degrees of freedom) areas to the left ofMxξwere 0.133, 0.039 and 0.0, respectively (i.e. correspondingPfdare 0.133, 0.039 and 0.0, respectively).

Apparently, it indicates that when the window size is set to 5, the target with velocity of 0.6 m/s is able to fulfill the requirements ofPfd.

Known in Figs.2,3, along with the increasing window size and target velocity, the overlapping area of centralizedχ2distribution (target remain static) and non-centralizedχ2distribution (target is moving) would be decreased. This will reduce the probability of false detection and the probability of leaking detection at the same time, with the disadvantage of increasing amount of calculation.

From above simulation results we can see that, the window size and target velocity significantly affect the test performance. In practice, it may choose properly size of window according to the system performance requirements.

3 Conclusions

This paper proposed a method of determining the static/moving state of targets, which is applied to MLAT system for airport surface surveillance. Using designed test statistics, this method constructs different PDFs to represent the static/moving state of targets, and uses it as the basis of binary hypothesis test. The main characteristics of this method are as follows:

(1) It eliminates the effects of GDOP on estimation error in MLAT system, which enables the test performance to have no connection with the relative geometric location between targets and stations;

(2) The size of sliding data window can be adjusted to fulfill different requirements of test performance.

As the theoretical basis of the state judging module in A-SMGCS, the proposed method has already been applied to the demonstration project of MLAT experimental system at Guilin Liangjiang International Airport.

Acknowledgement

This work was supported by the National Science and Technology Pillar Program of China (No.2011BAH24B06), the National Nature Science Foundation of China and Chinese Civil Aviation Jointly Funded Foundation Project (No.U1433129), and the Sichuan Provincial Department of Education Foundation (No.13ZB0287).

The authors would like to express their gratitude to Central and Southern Air Traffic Management Bureau of CAAC, Southwest Air Traffic Management Bureau of CAAC and Guilin Liangjiang International Airport.

[1] SHERMAN L, PER E. Capacity study of multilateration (MLAT) based navigation for alternative position navigation and timing (APNT) services for aviation [J]. Navigation, Journal of the Institute of Navigation, 2012, (59)4:263-279.

[2] GAVIRIA M, MAURO L, GASPARE G, et al. Localization algorithms for multilateration (MLAT) systems in airport surface surveillance [J].Signal, Image and Video Processing, 2014, 9(7):1549-1558.

[3] MAURO L, ADOLF M, GASPARE G. Closed form localization algorithms for mode s wide area multilateration[C]∥ Proceeding of the 6th European Radar conference, Rome, Italy: IEEE Press, 2009, 73-76.

[4] ROEDER M. EMMA-European airport movement management by A-SMGCS-A contribution to the vision 2020[C]∥ 25th Congress of the International Council of the Aeronautical Sciences, Hamburg Germany: Optimage, Ltd, 2006:4013-4019.

[5] MAURO L, SILVIO S, GASPARE G. ADS-B/MLAT surveillance system from high altitude platform systems[C] ∥2011 Tyrrhenian International Workshop on Digital Communications-Enhanced Surveillance of Aircraft and Vehicles, Italy, Capri: IEEE Press, 2011: 153-158.

[6] IVAN M, JUAN B, REYES L D, et al. Improvement of multilateration (MLAT) accuracy and convergence for airport surveillance[C]∥2011 Tyrrhenian International Workshop on Digital Communications-Enhanced Surveillance of Aircraft and Vehicles, Italy, Capri: IEEE Press, 2011: 185-190.

[7] IIN F, WANG H, WANG W, et al. Vehicle state and parameter estimation based on dual unscented particle filter algorithm[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2014,31(5): 568-576.

[8] HARRY L, VAN TREES. Detection, estimation, and modulation theory [M]. New York: Wiley Inter Science, 2001: 120-180.

[9] TODD K M, WYNN C S. Mathematical methods and algorithms for signal processing [M]. Upper Saddle River: Prentice Hall, 2000: 264-267.

[10]TONIERI D J. Statistical theory of passive location systems[J]. IEEE Trans on AES, 1984, (20)5: 183-198.

[11]CHAN Y T, HO K C. A Simple and efficient estimator for hyperbolic location[J]. IEEE Trans on SP, 1994, 42(8): 1905-1915.

[12]CHAN Y T, YAU H, HANG C, et al. Exact and approximate maximum likelihood localization algorithms[J]. IEEE Trans on Vehicular Technology, 2006, 55(1):10-16.

[13]HUANG J Y, WAN Q. Analysis of TDOA and TDOA/SS based geolocation techniques in a non-line-of-sight environment [J]. Communications and Networks, 2012, 14(5): 533-539.

[14]SHARP I, YU K. On the GDOP and accuracy for indoor positioning [J]. IEEE Trans on AES, 2012, 48(3): 2032-2051.

[15]HAHN W R, TRETTER S A. Optimum processing for delay-vector estimation in passive signal arrays [J]. IEEE Trans on Inform Theory, 1973, (19): 608-614

[16]YANG Lin, ZHOU Yiyu, XU Hui, et al. Passive location and error analysis using TDOA and aided height information by three stations[J]. Acta Electronica Sinica, 1998, 26(12): 71-74(in Chinese).

[17]SHARP I, KEGEN Y. GDOP Analysis for Positioning System Design[J]. IEEE Trans on Vehicular Technology, 2009, 58(7): 3371-3382.

[18]ZHANG Zhengchao, TONG Li. Precision Analysis of passive location of 4-stations based on TDOA [J]. Journal of China Academy of Electronics and Information Technology, 2010, 5(6): 582-587. (in Chinese)

[19]YUAN Gang, CHEN Jing. A clustering detection algorithm of stationary target for passive time difference location system [J]. Journal of Electronics & Information Technology, 2010, 32(3): 728-731. (in Chinese).

[20]CHAN Y T, TSUI W Y, SO H C, et al. Time-of-arrival based localization under NLOS conditions [J].IEEE Trans on Vehicular Technology, 2006, 55(1): 17-24.

Dr. Huang Rongshun is currently a Researcher in the Second Research Institute of CAAC. He received his Ph.D. in Sichuan University, and his main research interests focus on information processing and system integration.

Dr. Peng Wei is currently working as postdoctoral research fellow in University of Electronic Science and Technology of China. He received his Ph.D. in University of Electronic Science and Technology of China, and his main research interests are radar, digital signal processing and MLAT system.

Ms. Li Jing is currently an engineer in the Second Research Institute of CAAC, She received master degree in computer science and technology in 2008 from Northwest A&F University and her main research interests include MALT, ADS-B and A-SMGCS.

Dr. Wu Honggang is currently a researcher in the Second Research Institute of CAAC. He received his Ph.D. in Beijing University of Aeronautics and Astronautics, and his main research interests include signal processing and air traffic control systems.

Dr. Li Xingbo is the engineer of the Second Research Institute of CAAC. She received her Ph.D. in Warwick University, UK. Her research interests include multi-agent systems and swarm intelligence.

(Executive Editor： Zhang Bei)

TN958.97 Document code:A Article ID:1005-1120(2016)04-0425-08

*Corresponding author, E-mail address: pw7@163.com.

How to cite this article: Huang Rongshun, Peng We, Li Jing, et al.A test method for the static/moving state of targets applied to airport surface surveillance mlat system[J]. Trans. Nanjing Univ. Aero. Astro., 2016,33(4):425-432.

http://dx.doi.org/10.16356/j.1005-1120.2016.04.425