Sectorization Model of Terminal Airspace with Arrival and Departure Separation

,,

College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, P.R. China



Sectorization Model of Terminal Airspace with Arrival and Departure Separation

ZhangMing*,YuHui,ZhangMing

College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, P.R. China

(Received 18 November 2014; revised 2 January 2015; accepted 12 January 2015)

Terminal airspace (TMA) is the airspace centering several military and civil aviation airports with complex route structure, limited airspace resources, traffic flow, difficult management and considerable airspace complexity. A scientific and rational sectorization of TMA can optimize airspace resources, and sufficiently utilize the control of human resources to ensure the safety of TMA. The functional sectorization model was established based on the route structure of arriving and departing aircraft as well as controlling requirements. Based on principles of sectorization and topological relations within a network, the arrival and departure sectorization model was established, using tree based ant colony algorithm (ACO) searching. Shanghai TMA was taken as an example to be sectorizaed, and the result showed that this model was superior to traditional ones when arrival and departure routes were separated at dense airport terminal airspace.

air traffic management; arrival and departure sectorization model; controller′s workload; route structure of arriving and departing aircraft; Ant colony algorithm

0 Introduction

With the rapid development of air transport industry, air traffic flow is constantly roaring, and limited airspace resource has become the bottleneck of air traffic growth. Olaf et al. estimated[1]that the global air transport volume would reach three times of it now in 2025. Thus, it is pressing to upgrade the capacity of the air transportation system. Single European Sky ATM Research (SESAR)[1]and the U.S. Next Generation Air Transportation System (NextGen)[2]came up with the idea of establishing the next generation air transportation system in the coming 10 to 15 years. In this process, the effective management of air traffic resource is a key aspect. Terminal airspace (TMA) is an airspace centering the medium and low airspaces of several military and civil aviation airports with complex route structures, limited airspace resources, traffic flow, difficult management and considerable airspace complexity. A scientific and rational sectorization of TMA can optimize airspace resources, and sufficiently utilize the control of human resources to ensure the safety of TMA, thus improving the air traffic service capacity.

The theory and method of airspace sectorization has become the focus of airspace planning and management. In recent years, experts in this field have further underscored the mathematical models and algorithm to determine the sectorization plan, including graph theory, genetic algorithm and the design of computational geometry. Existing studies highlighted two-dimensional airspace[3-16]: Delahaye et al.[3]proposed the sectorization design based on genetic algorithm and computational geometry. Firstly, the method quantified the workload during control operation. Then, Voronoi algorithm of computational geometry was applied to the two-dimensional blocking of random airspace joints. Each Voronoi polygon contained different workloads. Eventually, with the optimization criteria of balanced workload, the sectorization goal could be met through genetic algorithm. Yet, as the method mainly used in randomly generated joints and chose the airspace for free flight as research background, it is not adequate for fixed route structure of existing airspacs. In addition, the research is confined in the two-dimensional airspace. Yousefi et al.[4-5]put forward a sector optimization method based on the workload of the controller. Firstly, they analyzed the acknowledging workload of controllers and the analysis model of airspace complexity. Next, according to the operating altitude scope, the national airspace of America was divided into three layers as low altitude, high altitude and super altitude. Each layer could be further divided into 2 566 hexagons, each of which had a side length of 24 nautical miles. Hexagons compromised the basic design unit of the airspace. Next, the temporal and spatial distribution of workloads in the airspace and terminal area was identified to acquire the crowded period of time of national airspace of America. Ultimately, the clustering algorithm of optimization theory was applied to the combination of hexagon groups to divide the controlling center and sector boundary of the U.S. national airspace. Compared with the study of Delahaye, this study also took the perspective of basic design unit and controllers′ workloads, while holding better practical values. However, this study still limited in three aspects: The study targeted at the en-route control area, failing to refer to TMA ; with the consideration of the operative convenience of controllers, this study ignored dynamic sectorization; in addition, key limitation conditions such as the design of conflict points were not considered in this study. On the basis of the above mentioned research, scholars from Europe and America conducted consecutive studies on this. For example, Verlhac et al.[6]proposed a integer design technique; D. Gianazza et al.[7]developed a tree search algorithm. Huy Trandac et al.[8]proposed a constraining design method of airspace sector. Davide Famanelli et al.[9]introduced the graph theory to the optimization of airspace. The existing research findings[10-16]have laid valuable foundation for our research.

In TMA segment design, the sectorization was conducted according to the arrival and departure function of aircraft[17]. Meanwhile, the vertical interval between the arrival and the departure routes was drawn out to ensure security. Controllers′ command can line up aircraft arrived from corridor entrance, which are directly handed over to the final of the airport. Departure aircraft are directly handed over to adjacent regions through departure control. Currently, in the sectorization based on geographical regions, a complete arrival and departure route is often divided into an array of sectors, generating extra control transferring workloads between sectors. Thus, according to the arrival and departure function of aircraft, the sectorization can keep the relevant coordination to the lowest level, and maintain the climbing performance of departure aircrafts close to the optimum level, thus ensuring the orderly safe arrival and departure. The approach is especially necessary for complex TMA with multiple airports (such as Shanghai TMA) because it can effectively avoid frequent transfer and cooridnation of arrival and departure flows among different airports, which greatly alleviates workloads of control and flight. Although sectorization has been applied to those international terminal areas with considerable traffic density, most existing approaches used qualitative design, which fails to provide efficiency and accuracy for sectorizing dense terminal areas of airports. Therefore, we established arrival and departure sectorization model considering arrival and departure separation.

1 Arrival/Departure Sectorization Model

1.1 Route of controller workloads

Typically, controllers′ workload can be described as: The airspace is divided into a number of sectors, each of which is assigned to a group of controllers. Controllers of each sector are required to complete the monitoring of flights to avoid conflicts among aircraft, and to exchange information with adjacent sectors in the planned routes of aircraft. These tasks can be divided into three parts: Supervision workload, conflict workload and coordination workload.

Workloads of controlling command are mapped to the routes. The route network can be expressed as a weighted graph G=(V, E), where V is the set of vertices, that is, the set of navigation stations and intersection pointsu; E the set of sides. In addition, when and only when a straight route exists fromutov, (u,v) ∈E,thecontrollingworkloadsontheroutescanbeexpressedas

(1)

where,ωeis the weight of controlling workloads of routee;cu,cvare conflict workloads rising from the conflicts ofuandv;methe monitoring workloads, belonging to a sidee=(u,v), and it has been divided into two equal partsmu=mv=me/2, which are assigned touandv;oethe coordination workloads, which are assigned to sidee. If the vertices of a side fall in one sector,oe=0. The load weights ofV-Eon the route then can be calculated. Therefore, each route can be set as a finite element, and has a weight of controlling workloads.

1.2 Distribution of controller workloads in airspace

On the basis of airspace traffic flow prediction and historical data of TMA workloads, TMA controlling workloads can be distributed according to Canching schedule of the controlling command, and then mapped to the three-dimensional terminal airspace route network. Therefore, the distribution of workloads in the route network is determined. We also presented a centroid method of controlling workloads as follows.

In order to illustrate the airspace distribution of controlling workloads, the regional distribution of controlling workloads can be concentrated on a centroid point, that is, the centroid of controlling load unit. In accordance with the weight distribution in physics, the centroid can be identified as the center-of-gravity position of controlling workloads.

Assume that the controlling load finite elementiobtainsNcontrolling load points, and thejcontrolling load point is presented as (xj,yj), so that the centroid is

(2)

Through the acquiring raw data of flight flow distribution the airspace distribution of controlling workload centroid is identified.

1.3 Topological presentation of route network

If the computer is used in the TMA optimized sectorization, data collection of controller workloads and mathematical description of TMA structure on the route should be accomplished first so that the topological relationship matrix among the route finite elements can be built up.

A route that connected nodes, like navigation stations, the airports and position reporting points can be divided into a limited number of routes. A route is the basic finite element of optimized sectorization, and the topological relationship matrix among the route finite elements can be established. Straight routes of routes in TMA are expressed by the set R=[r1,r2, …,rn]T, and the topological matrix among routes in the airspace can be expressed as

(3)

where the elements of matrix G havegij∈{0, 1}.gij=1 shows the correlation between routeiand routej;gij=0 shows the irrelevance ofiandj;nis the route number in TMA serving as the basic finite elements for the optimizing search of sectorization.

1.4 Calculation model of sector number

According to the DORATASK method recommended by ICAO[18], the average workloads of controllers should be less than 80% of the time statistics. Based on this principle, it should be ensured that the total workloads in the airspace is minimized. Firstly, the total workloadsWTof controlling in the airspace should be collected andNs, the number of divided sectors should meet the following equations whereSis the statistical time of sector; and int the rounding function;Nsthe minimum number of sectors.WTis the total airspace workloads, which is expressed by time. When the result ofMis not an integer, the calculation results should be rounded plus 1 to reachNs; ifMis an integer,Nsis directly obtained.

(4)

(5)

1.5 Sector optimization target model

The bi-level optimization model of sectors is built under the premise of the estimated minimum number of sectors. The target is to achieve the sector load balance under the premise of the minimum total load in TMA. The following model was thus built up

(6)

whereωciis the fixed load oni, including monitoring loads and coordination loads;ωvjthe transferred load of sectors;sthe number of finite element divided in the airspace.

On the basis of the model which ensured the minimum load of TMA, the secondary target of sector optimization is to meet the balance of controller′s workloads among all sectors

(7)

whereωkis the workload of theksector andμis the average load ofNssectors.

In the actual division of the sectors, in addition to the impact of capacity and load, we should also consider the actual controlling states and airspace rules so that the following optimization constraints should be introduced in the operation.

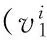
(1) Functional constraints of sectors

In order to acquire the functional uniformity of route finite element in each sector, functional constraints of sectors should be included, which can be illustrated by the conflicts in finite elements and nature of controlling commands. Generally, a sector can hold the same arrival controlling or departure controlling, so as to maximize the reduction of coordination loads.

(2) Minimum sector crossing time constraints

To ensure the operation margin of deployment and instructions of the air controllers (Fig.1), aircraft should stay in the sector longer than the set minimum time duration, i.e.Tmin.Tminvalue should be two times ofωc, the time of the transfer of instruction, i.e.

(8)

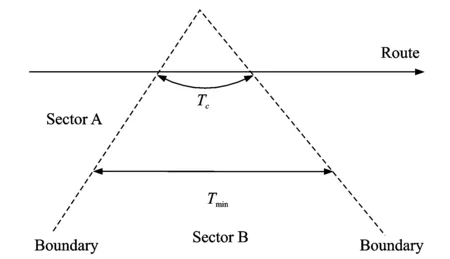
Fig.1 Minimum sector crossing time constraints

(3) Minimum distance constraints of the sector boundary rendezvous points (the intersections)

The distance of the sector boundary rendezvous points must be longer than a given value, which can provide sufficient time for controllers to deal with conflicts at nodes, so as to prevent aircraft of other sectors from entering the nodes and therefore avoid new conflicts (Fig.2).

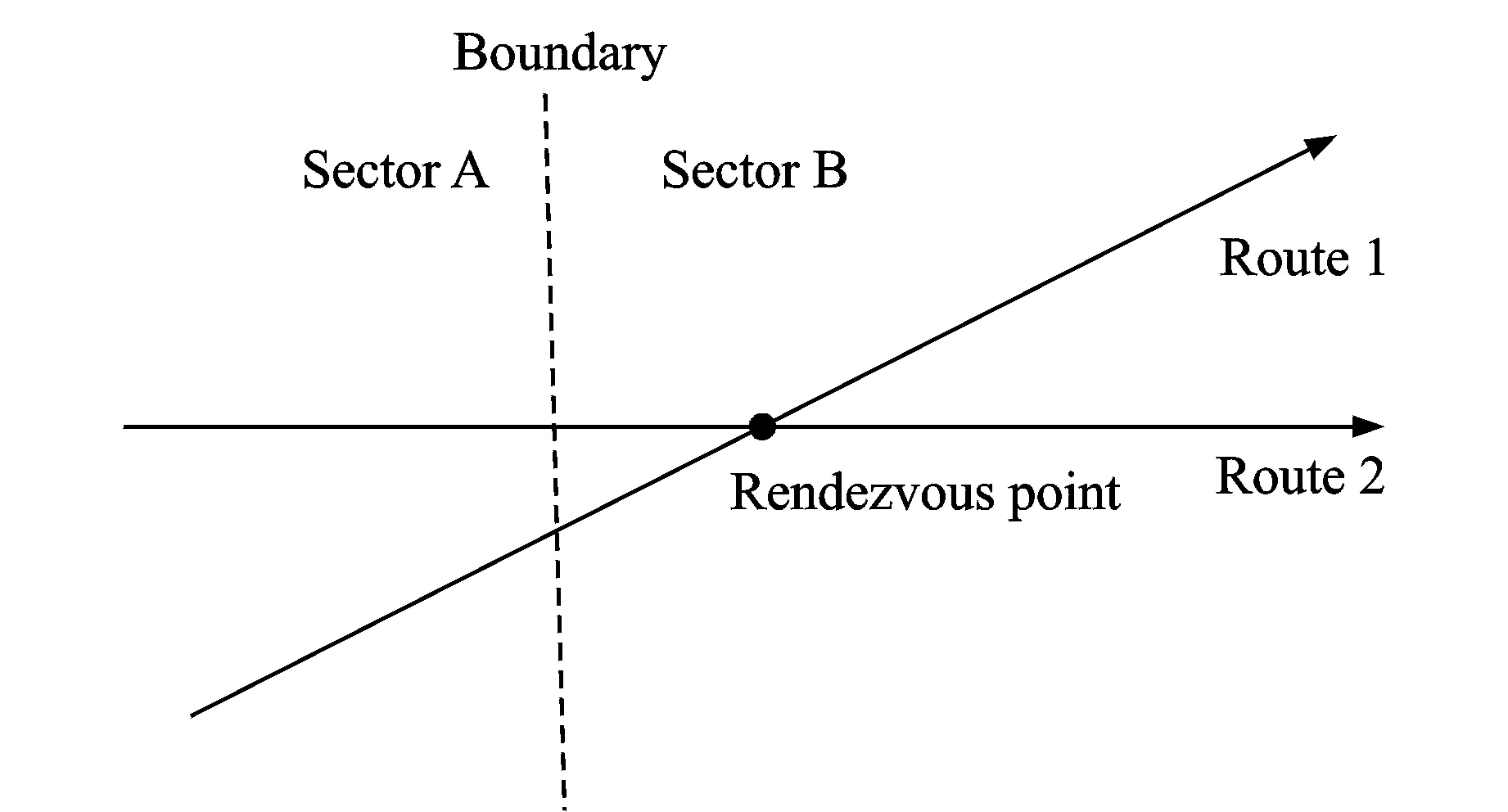
Fig.2 Minimum distance constraints of the sector boundary rendezvous points (the intersections)

Set required time of controllers to solve the conflict at the nodes asωf, the transfer time of sector asωc, aircraft interval asωj, and the minimum time for the sector boundary and nodes is

(9)

(4) Convex constrains

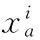
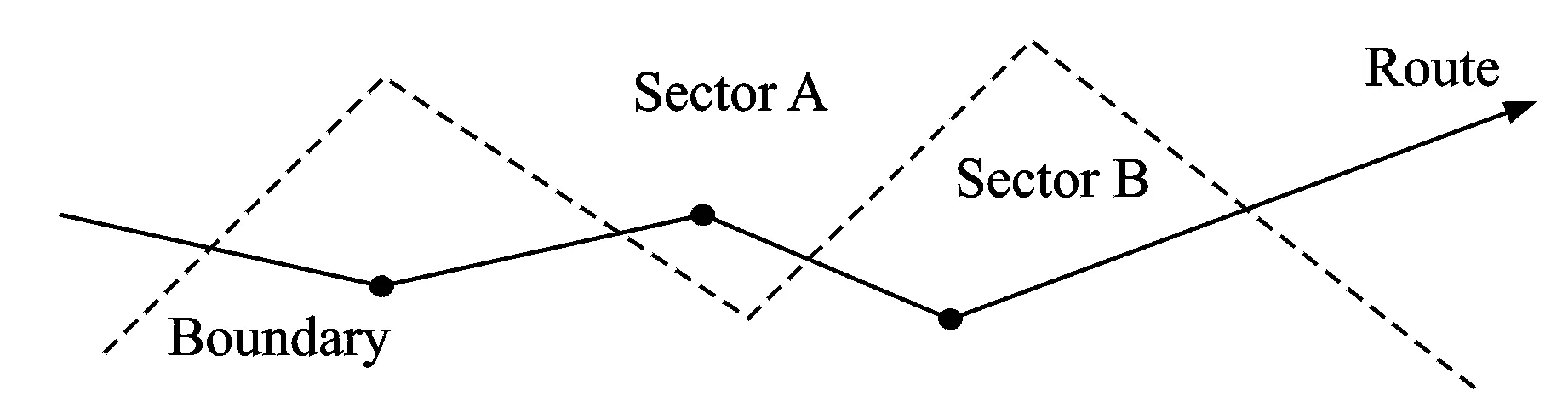
Fig.3 Convex constrains of sectors

1.6 Sectorization optimization algorithm

Ant colony algorithm is completed in following steps.

Step 1 Initialize the route finite element properties in TMA. Set arrival as 1, departure and combined arrival and departure as 0. The load value of each finite element is acquired from the investigation data, and the initial transfer intensity and visibility of each unit is set.

Step 2 Select the initial search finite element. For internal and external sectors, the last approaching finite element is taken as the initial unit. For those with busy routes as the center, the corridor entrance finite element can be selected. The property of this entrance finite element is 1 to form the initial sector.

Step 3 For Antiin Groupj, the sub-unit correlated with current sector can be selected. If correlated, the query Table A is stored to calculate the transfer probability of each unit. According to the probability interval, the entering unit can be selected. Meanwhile, the cumulative strength of the transfer of the finite element can be updated. Ifi=n(when ants of this group finish the query, and transfer intensity is transferred), the cumulative intensity is assigned to the transfer intensity of the unit.

Step 4 Collect the loads of sectors. If the load meetsWi≤S×80%, go to Step 5. If not, go to Step 3.

Step 5 Determine the target function. If improved, the combination is recorded, other wise the previous record is maintained.

Step 6 Output the eventually optimized target function and combination of controlling load.

2 Analysis of Examples

2.1 Route load statistics of Shanghai TMA

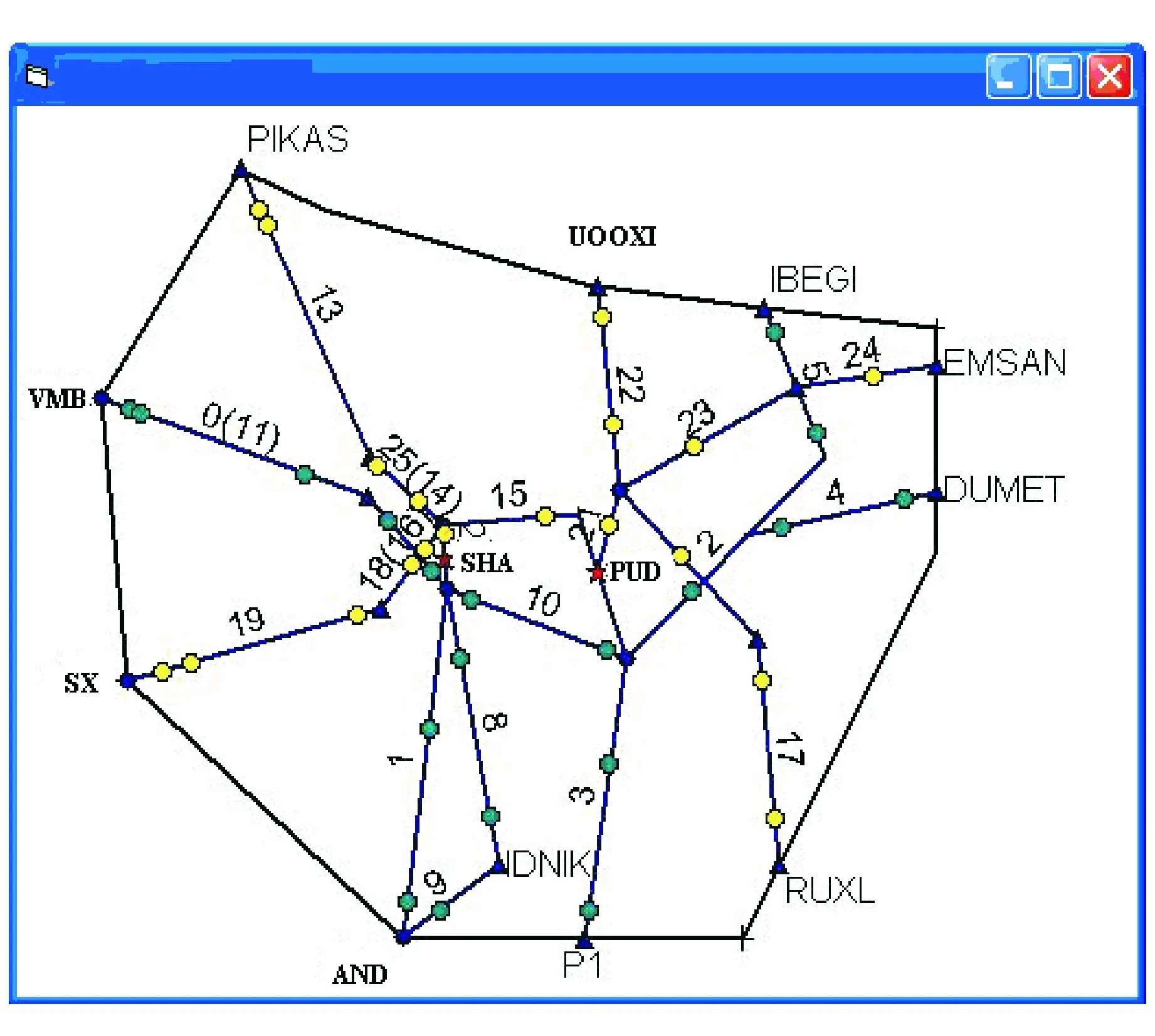
Fig.4 Route distribution of Shanghai TMA

Based on the real-time radar voice data of Shanghai TMA and the controlling instruction distribution range, all arriving flights of Shanghai TMA were divided into four states: Initial contact, control altitude, waiting or motor deployment and control speed. Similarly, all departure flights were divided into three states: Initial contact, control altitude and departure transfer. Through navigation stations, airports, location report spots and so on, routes were divided into finite element and numbered. The entire route of TMA was divided into 26 units. Fig. 4 shows the finite element division and centroid point distribution of this TMA. According to the traffic flow, the distribution of controlling workloads of each finite element (time) in Shanghai TMA as well as the geographic data of each airspace finite element can be estimated, as shown in Table 1. Meanwhile, the topological relationship matrix of various finite elements was obtained as shown in Table 2.

Table 1 Route load of Shanghai TMA

2.2 Shanghai TMA functional sectorization

We established air traffic microscopic simulation system using Microsoft Visual Basic 6.0 to verify the rationality of Shanghai TMA sectorization. We facilitated computer simulation technology to realize dynamic simulation of controller′s instructions, as well as the statistic analysis of controller workloads in this sector. The data was reasonably inferred from the actual condition of Shanghai TMA. In addition, through the access to the finite element database and airspace controlling load database, we collected the controller′s workload on each unit. The ant colony algorithm was used for optimized search.

Table 2 Topological relation matrix of 26 finite element

According to Eqs. (4), (5), the aircraft controlling workloads (without considering the loads of east-west Pudong sectors) were substituted, whereWT=10 567 s andS=3 600 s, and we obtained thatNs=4. In other words, the minimum sector number was 4.

In the optimized sectorization model, ant colony algorithm was used to optimize this model and combine the finite element according to the functional uniformity. The sectorization result is shown in Table 3.

As the sector was expanded from the finite element to the airspace, the qualitative design ensured the safety interval of departure routes and the protection range of intersections. Therefore, final optimized sectorization was achieved. Fig. 5 shows the three dimensional graphs of 6 functional sectors with NX7.0 CAD.

2.3 Analysis on Shanghai TMA micro-simulation system

For the two plans of sectorization, 30 groups of flow data in peak hours in the design year were simulated. The simulation results were statistically analyzed (Table 4).

Simulation and analysis indicators of TMA air traffic micro-simulation system (Fig.6) were hourly controller workloads, that is, workloads of air traffic controlling in an hour for one controller. We analyzed whether loads in each sector meet the controller workloads defined in DORATASK. The north orientation arrival of Shanghai TMA was taken as an example to simulate the peak hour flow of future plans of sectorization, and the results were analyzed statistically.

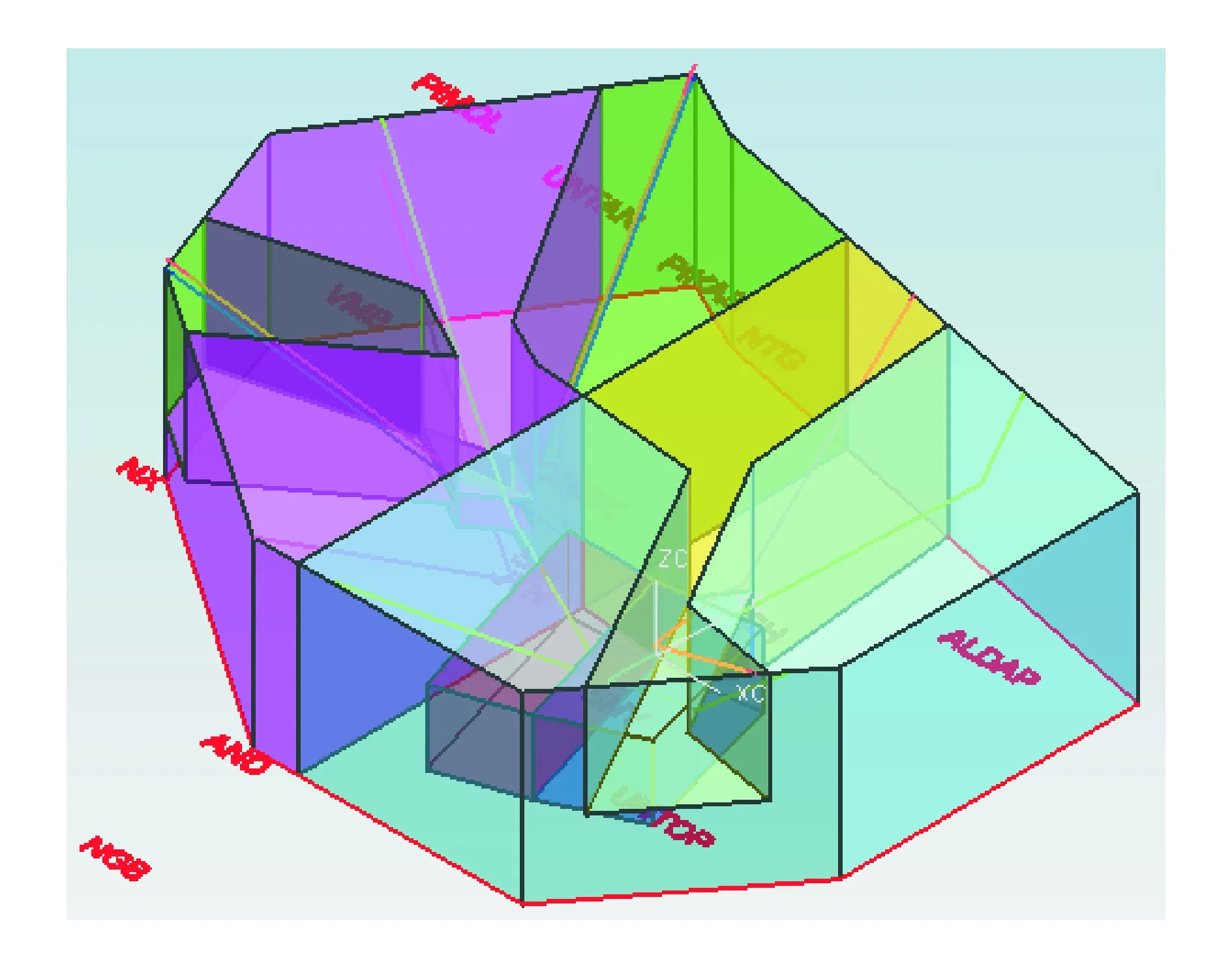
Fig.5 The space diagram of north orientation sectorization of Shanghai TMA

Plan A applied regional functional sectorization and Plan B utilized the traditional geographic sectorization. Plan A divided TMA into 6 sectors (including 2 sectors of east-west entrances of Pudong Area). Plan B divided TMA into 7 sectors. For the two plans, 30 groups of peak hour flow data in 2012 were simulated, and the average controller workloads of each sector are shown as follows.

Table 4 shows that Plan B achieved uniform load distribution and the total load of Plan B was larger than that of Plan A. Controller workloads of each sector in the two plans were less than 2 880 s, which met the controller workloads as defined in DORATASK. Thus, the operation workloads were greatly improved for controllers.

Table 3 Departure sector load distribution after optimized sectorization

Table 4 Comparison of two plans of hourly peak controller workload of each sector in 2012 s

Therefore, compar326asion between the two sectorization plans interms of airspace performance indicators showed that although functional sectorization could not optimize the balance of sector loads, it could effectively reduce the controlling airspace difficulty, as well as the coordination workloads. Thereby, it reduced the workloads of the entire airspace, expanded the airspace capacity, and optimized the operating environment of airspace. Hence, the sectorization with the separation of arrival and departure efficiently alleviated the pressure imposed by limited airspace resources, presenting outstanding advantages for the sectorization of TMA with frequent flight conflicts.

3 Conclusions

The functional sectorization model is established based on the characteristics of the route structure of seperated arriving and departing aircraft as well as the operation requirements of controlling. The quantitative, simulation and comparative study illustrated that the functional design of airspace sector overweighed the geographic design by reducing controller workloads and airspace delay. In this study, tree theory of airspace delay was used in the sectorization of the arrival and departure separation. Based on constraints of sectorization and topological relations in the network, the ACO search was used to establish the arrival and departure sectorization model. The quantitative results were achieved.

In future research, the dynamic sectorization of TMA with the complex air traffic and climates would be the focus.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. U1233101, 71271113) and the Fundamental Research Funds for the Central Universities (No.NS2016062).

[1] OLAF D, THORSTEN A, CRISTIANO B. SESAR D3 ATM target concept[R]. DLM-0612-001-02-00a. Brussels, Belgium: EUROCONTROL, 2007: 19-23.

[2] SWENSON H, BARHYDT R, LANDIS M. Next generation air transportation system (NGATS) air traffic management (ATM) -airspace project, reference material[R]. Silicon Valley CA: NASA Ames Research Center, 2006: 31-35.

[3] DELAHAYE D, SCHOENAUER M, ALLIOT J M. Airspace sectoring by evolutionary computation[C]∥IEEE World Congress on Computational Intelligence, CMAPX/LOG. France: IEEE, 1998: 218-223.

[4] YOUSEFI A. Optimum airspace design with air traffic controller workload-based partitioning[D]. USA: George Mason University, 2005.

[5] YOUSEFI A. DONOHUE G L. Temporal and spatial distribution of airspace complexity for air traffic controller workload-based sectorization[C]∥AIAA 2004-6455∥AIAA the fourth Aviation Technology, Integration and Operations (ATIO) Forum. Chicago, IL, USA: AIAA, 2004: 1-14.

[6] VERLHAC C, MANCHON S. Optimization of opening schemes[C]∥Proceedings of the fourth USA/Europe Air Traffic Management R&D Conference. Santa Fe, NM, USA: FAA, 2001: 1-11.

[7] GLANAZZA D, ALLIOT J M. Optimization of air traffic control sector configurations using tree search methods and genetic algorithms[C]∥Digital Avionics Systems Conference. Toulouse, France: IEEE, 2002: 1-9.

[8] TRANDAC H, DUONG V. Optimized sectorization of airspace with constraints[C]∥Proceedings of the fifth USA/Europe Air Traffic Management R&D Conference. Budapest, Hungary: [s.n.], 2003.

[9] FAMANELLI D. a k-partitioning algorithm for airspace sectorization[D]. USA: Padova University, 2005.

[10]SABBNANI G. Geometric algorithms for the airspace sectorization problem[C]∥Proceedings of the fifth USA/Europe Air Traffic Management R&D Conference. Budapest, Hungary: EUROCONTROL, 2003.

[11]MAJUMDAR A, OCHIENG W Y, BENTHAM J, et al. En-route sector capacity estimation methodologies an international survey[J]. Journal of Air Transport Management, 2005,11(6): 375-387.

[12]XUE M. Airspace sector redesign based on voronoi diagrams[J]. Journal of Aerospace Computing Information and Communication, 2009, 6 (12): 624-634.

[13]CONKER R S, MOCH-MOONEY D, NIEDRINGHAUS W P, et al. New process for clean-sheet airspace design and evaluation[C]∥the seventh USA/Europe Air Traffic Management R&D Conference. Barcelona, Spain: EUROCONTROL, 2007: 1-10.

[14]BASU A, MITCHELL J S B, SABBNANI G K.Geometric algorithms for optimal airspace design and air traffic controller workload balancing[J]. Journal of Experimental Algorithmics, 2009,14 (3): 75-89.

[15]TANG J J, ALAM S, LOKAN C, et al. A multi-objective approach for dynamic airspace sectorization using agent based and geometric models[J]. Transportation Research Part C: Emerging Technologies, 2012, 21(1): 89-121.

[16]GLANAZZA D. Airspace configuration using air traffic complexity metrics[C]∥The Seventh USA/Europe Air Traffic Management R&D Conference. Barcelona, Spain: EUROCONTROL, 2007: 1-11.

[17]LAMBERT J, HENDRICKS A, PHILIPP W. Terminal airspace design guidelines for an operational methodology[R]. ASM.ET1.STO6.DEL01, Brussels, Belgium: EUROCONTROL, 1998: 21-26.

[18]WANG Chao, HE Chaonan. Three-dimensional planning of arrival and departure route network based on improved ant-Colony algorithm[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2015, 32(6): 654-664.

[19]International Civil Aviation Organization (ICAO). Doc9426-AN/924-1992, Manual for air traffic service plan[S]. Montreal, Canada: ICAO, 1992.

Dr. Zhang Ming is currently an associate professor in College of Civil Aviation, Nanjing University of Aeronautics and Astronautics. He received his Ph.D. degree in transportation engineering from Nanjing University of Aeronautics and Astronautics in 2010. His research interests include airspace management, aviation rescue and flight safety.

Ms. Yu Hui is currently a M.S. candidate of College of Civil Aviation, Nanjing University of Aeronautics and Astronautics. Her research interests include air traffic control.

Mr. Zhang Ming is currently a M.S.candidate of College of Civil Aviation, Nanjing University of Aeronautics and Astronautics. His research interests include air traffic control.

(Executive Editor: Zhang Bei)

V355.2 Document code:A Article ID:1005-1120(2016)04-0442-09

*Corresponding author, E-mail address: zhangm@nuaa.edu.cn.

How to cite this article: Zhang Ming, Yu Hui, Zhang Ming. Sectorization model of terminal airspace with arrival and departure separation[J]. Trans. Nanjing U. Aero. Astro., 2016,33(4):442-450.

http://dx.doi.org/10.16356/j.1005-1120.2016.04.442