高中数学思维指导下的解题技巧
2016-11-19江苏省常熟市中学张静芬
☉江苏省常熟市中学 张静芬
高中数学思维指导下的解题技巧
☉江苏省常熟市中学张静芬
高中阶段数学学科依然占据主要地位,数学考试也是备受学生和家长关注.试卷中各种数学题型变幻莫测,各方面知识点考查齐全,经常让学生应接不暇.课下有学生反映考试时数学卷做不完、检查没时间,手慢脚乱忙了一阵,成绩也不理想,这让很多学生和家长感到苦恼,要想改善这种状况其实诀窍就在于能否熟练地掌握解题技巧.解题技巧不是孤立的,要在一定的数学思维指导下,这样学生才能掌握数学的精髓,无论题型如何变幻,都能应对自如.
班里经常有这样的孩子,平时非常用功,抓紧每一分每一秒学习,甚至吃饭的时候都是一边端着碗一边看着书,尽管如此,学习效果却不是很理想,为此他们非常苦恼.其实高效的学习不应该是一味、单纯地挖知识,一定要有科学、合理的思想来指导.知识是肉身,思想是灵魂,它们相辅相成缺一不可,没有知识的思想只是一具空壳,没有思想的知识也只是行尸走肉,只有知识和思想相结合才是真正的学习.高中数学一直是学生们望而生畏的一门课程,很多学生苦苦专研,也找不到解题的要领,所以,教师要教会学生站在思想的高度掌握解题技巧.
一、发散性思维指导下的图解法
学习数学避免不了要应用到图形,它是解决数学难题不可或缺的一种辅助手段,图形一出现很多已知条件跃然图中,很容易找到解题的突破口.但是,找到突破口也要带着目的性、选择性,不能全部拿来,眉毛胡子一把抓.要求学生要具有发散思维,化抽象为具体,化复杂为简单,以不变对万变.先综合所有已知条件思考整个问题,在把握大局的前提下分清主次,接下来抓住主要的特征,从主要的思维角度入手,一步一步达到解决问题的目的.
分析:此题中不等式的两边都是基本函数,左边是指数函数,右边是对数函数,充分利用此特征,作出两个函数图像,利用图解法能更好解决此题.在高中数学中,利用图解法,可以比较函数值的大小,确定参数范围,也能利用图像解决一些方程的解和零点问题等.
因为logax>4x>1,所以0 令f(x)=4x,g(x)=logax,如图1,当 图1 又因为g(x)=logax,x0∈(0,1),a1,a2∈(0,1)且a1 图解法有图形,有数字,有已知条件,有相关结论.一个图形,多个数量关系,把它们紧密地结合在一起,先分解,后整合,也是对学生发散性思维的一种锻炼.这种方法的应用范围很广,高中数学的学习过程中会经常用到,有时只在草纸上操作,简单易行.我们要学会掌握这种方法的精髓,而不是只了解简单的皮毛,争取把它内化为自己的一种本领.本领在手,不光是数学学科可以用,其他学科也能用得到,乃至以后遇到其他事情也可以用到这种思维方式.. 高中数学有很多题涉及到函数、导数,对学生来说个个都是难关,非常苦恼.变量代换法既能解决这些难题,又便于学生掌握,教学中值得传授.变量代换,简单地说就是引入一个变量,运用相关知识予以技巧性的变化来替换已知条件中的某些定量,得到新的变量,接下来再展开对新变量的研究,把研究结果代入原式得出我们要的结论.这种替换可以连接已知和未知,相当于借助中介的力量转化原问题的难度,达到简化的目的.这种方法如果用的恰到好处,可以收到事半功倍的效果. 例2不等式x+y≤k(2x+y)对任意正实数x、y恒成立,求k的取值范围. 分析:这道题中涉及到两个变量和一个参数,这样会使学生有点手足无措.如果能将两个变量转化为一个变量,这样会使得题目更容易解决.所以解题时需先引入一个新的变量,变量的介入让不等式改变了原形,再对变形后的新变量进行讨论.此题先把两端分别除以y变量,即可得到,这样由原来的x、y两个变量变为,然后进行变量分离,可得,因为2t+1>1,所以1,最后可得k≥1,则k的取值范围为[1, +∞). 另外还有很多类似的题目都可以采用此方法来解决.例如:已知不等式x2+y2≥k·2xy对任意正实数x、y恒成立,求k的取值范围.此题可以两边同除以2xy,可得k≤再利用基本不等式可得k≤1. 提到观察法很多学生会认为这是物理和化学学科常用的方法,数学就应该是计算,其实不然,数学学科有很多问题通过观察也能找到我们想要的答案.当然这里说的观察不是漫无目的地瞅来瞅去,而是带着寻找答案的目的,发动我们的感官去观察.另外,这里说的观察也不是只抓问题的一部分,而是要从整体上把握问题的脉络.所以,细说起来,观察法运用的过程中心要细,眼要尖,这样才能寻找突破口,抓住关键,厘清解题思路,做了这些铺垫什么问题都不难了. 本题就是通过直接观察获取答案的典型例题,适合一类函数值域的求法,一目了然.当然在实际做题过程中很多习题难度要比这个多很多,但是解题思路都是一样的.主要是通过此种方法培养学生的观察能力,它是一名优秀的学生应该具备的基本素质.无论是学习还是生活具备观察能力都是孩子们具有一项生存技能.善于观察才能发现事物的前因和后果,才能分辨出事情的真实和虚伪,才能发现解决问题的方案和技巧,最后才能做学习的强者. 在数学领域思考问题,我们习惯于逻辑推理,从已知推出结论.但在做题的过程中常常会遇到从正面证明有困难,或者情况比较多挺复杂,而反面只有一种情况,相对简单,这时可以考虑用反证法.所谓反证,就是从反面入手去证明,打破了常规的思维模式,有另辟蹊径的感觉.一般不等式证明常用它,如果题中含有“至多”、“至少”、“均是”、“不都”、“任何”、“唯一”等字眼就具备了用反证法的条件了.反证法思维方式独特,开阔眼界,能够培养学生的逆向思维能力. 例4如果p1p2=2(q1+q2),求证;二次函数y=x2+p1x+ q1和y=x2+p2x+q2的图像至少有一个与x轴相交. 分析:该题如果直奔主题去求解很难,不知道从何处下手,无法断定哪一个函数的图像与x轴相交.那么我们不妨从问题的另一面去考虑,也就是反其道而行之,假设y=x2+p1x+q1和y=x2+p2x+q2的图像都不与x轴相交,便得到两个判别式,再加上p1p2=2(q1+q2)这个已知条件,代入求得,即能判断能否与x轴相交. 证明:假设二次函数y=x2+p1x+q1和y=x2+p2x+q2的图像都不与x轴相交,则有 又因为p1p2=2(q1+q2), 所以2p1p2=4(q1+q2), 通过上题的分析让我们找一找反证法的适用条件.此题已知条件较少,就只有p1p2=2(q1+q2)一个,而且它和问题之间关系不是很直接,再加上问题“y=x2+p1x+q1和y= x2+p2x+q2的图像至少有一个与x轴相交”相对来讲很抽象,不具体.而其反面结论恰恰相反,不但具体,还容易入手,这种情况最适合运用反证法,这是一种逆向思维方式,打破常规,实际做题过程中多加训练就很容易掌握. 数学思维的有效培养可以形成数学素养,数学方法的掌握可以提升学生解题效率.数学思维方式不是与生俱来的,是在不断的学习知识,掌握和运用方法的基础上形成的,数学解题方法也不是一学就会的,是在数学思维的指导下,不断的实践和训练慢慢掌握的.所以,要想在数学上得高分就必须开拓思维,认真研究,多方面挖掘,总结和掌握各种解题技巧,技巧熟练,运用自如,才能及时答疑解惑,拓展思路,发展智力. 1.曾定.浅谈高中数学解题反思[J].高中数学教与学,2013(12). 2.曾庆珊.高中数学四种解题教学模式的教学实践研究[D].长沙:湖南师范大学,2014. 3.谈敏.逆向思维在高中数学解题中的一些应用[J].语数外学习(数学教育),2013(12).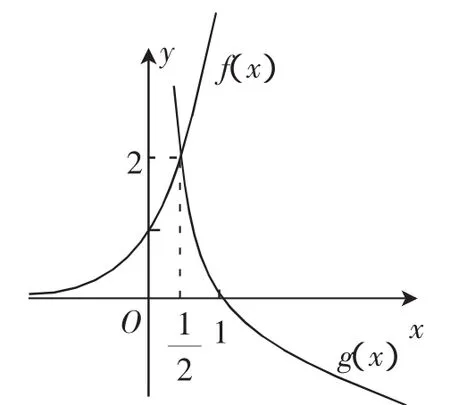
二、创造性思维指导下的变量代换
三、逻辑性思维指导下的观察法
四、逆向思维指导下的反证法
